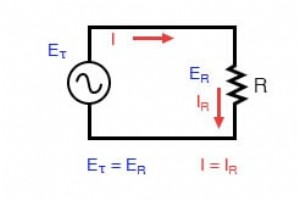
Directe waarden in AC-circuits Puur resistief AC-circuit:weerstandsspanning en stroom zijn in fase. Als we de stroom en spanning zouden plotten voor een heel eenvoudig wisselstroomcircuit bestaande uit een bron en een weerstand (figuur hierboven), zou het er ongeveer zo uitzien:(figuur hierond

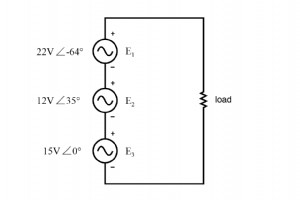
Laten we drie wisselspanningsbronnen in serie aansluiten en complexe getallen gebruiken om additieve spanningen te bepalen. Alle regels en wetten die zijn geleerd in de studie van DC-circuits zijn ook van toepassing op AC-circuits (de wet van Ohm, de wetten van Kirchhoff, netwerkanalysemethoden), m

Complexe getallen zijn handig voor AC-circuitanalyse omdat ze een handige methode bieden om symbolisch faseverschuiving aan te duiden tussen AC-grootheden zoals spanning en stroom. Voor de meeste mensen is de gelijkwaardigheid tussen abstracte vectoren en reële circuitgrootheden echter niet gemakke

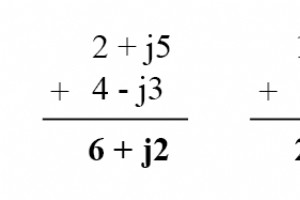
Aangezien complexe getallen legitieme wiskundige entiteiten zijn, net als scalaire getallen, kunnen ze worden opgeteld, afgetrokken, vermenigvuldigd, gedeeld, gekwadrateerd, omgekeerd en dergelijke, net als elk ander soort getal. Sommige wetenschappelijke rekenmachines zijn geprogrammeerd om deze b

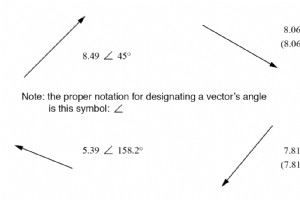
Om met complexe getallen te werken zonder vectoren te tekenen, hebben we eerst een soort standaard wiskundige notatie nodig. Er zijn twee basisvormen van complexe getalnotatie:polair en rechthoekig . Polaire vorm van een complex getal De polaire vorm is waar een complex getal wordt aangegeven met d

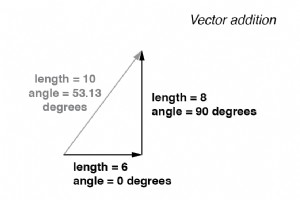
Als vectoren met ongewone hoeken worden opgeteld, tellen hun magnitudes (lengtes) heel anders op dan die van scalaire magnitudes:(figuur hieronder) Vectorgrootheden worden niet direct opgeteld voor ongelijke hoeken. Als twee wisselspanningen (90° uit fase) bij elkaar worden opgeteld door ze

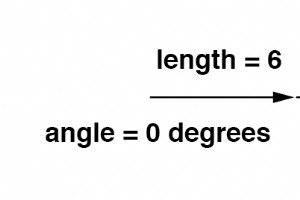
Onthoud dat vectoren wiskundige objecten zijn, net als getallen op een getallenlijn:ze kunnen worden opgeteld, afgetrokken, vermenigvuldigd en gedeeld. Optellen is misschien wel de gemakkelijkste vectorbewerking om te visualiseren, dus daar beginnen we mee. Als vectoren met gemeenschappelijke hoeken

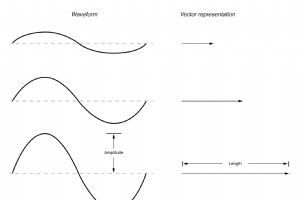
OK, dus hoe kunnen we AC-hoeveelheden van spanning of stroom precies weergeven in de vorm van een vector? De lengte van de vector vertegenwoordigt de grootte (of amplitude) van de golfvorm, als volgt:(figuur hieronder) Hoe groter de amplitude van de golfvorm, hoe groter de lengte van de bijbe

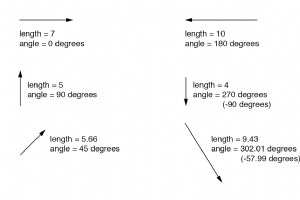
Als ik de afstand tussen twee steden zou moeten beschrijven, zou ik een antwoord kunnen geven dat bestaat uit een enkel getal in mijlen, kilometers of een andere lineaire meeteenheid. Als ik echter zou beschrijven hoe ik van de ene stad naar de andere moet reizen, zou ik meer informatie moeten vers

Een van de meest fascinerende toepassingen van elektriciteit is het opwekken van onzichtbare rimpelingen van energie die radiogolven worden genoemd. . De beperkte reikwijdte van deze les over wisselstroom laat geen volledige verkenning van het concept toe, enkele basisprincipes zullen worden behande

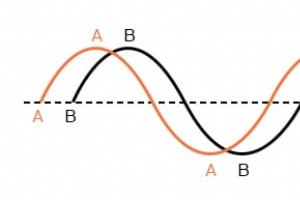
Dingen beginnen ingewikkeld te worden wanneer we twee of meer wisselspanningen of -stromen moeten relateren die niet met elkaar in overeenstemming zijn. Met uit de pas bedoel ik dat de twee golfvormen niet gesynchroniseerd zijn:dat hun pieken en nulpunten niet op dezelfde tijdstippen overeenkomen. D

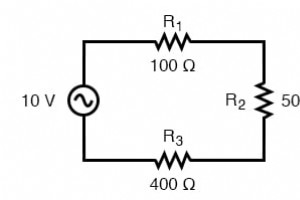
In de loop van de volgende hoofdstukken leert u dat het meten en berekenen van wisselstroomcircuits erg ingewikkeld kan worden vanwege de complexe aard van wisselstroom in circuits met inductantie en capaciteit. Met eenvoudige circuits (figuur hieronder) die niets meer dan een wisselstroombron en w

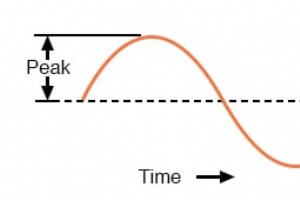
Tot nu toe weten we dat wisselspanning wisselt in polariteit en wisselstroom wisselt in richting. We weten ook dat wisselstroom op verschillende manieren kan worden afgewisseld, en door de afwisseling in de tijd te volgen, kunnen we deze plotten als een golfvorm. We kunnen de afwisselingssnelheid m

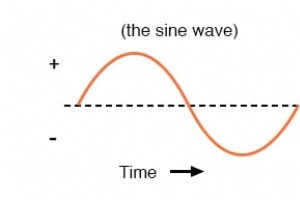
Wanneer een dynamo wisselspanning produceert, verandert de spanning in de loop van de tijd van polariteit, maar dit op een heel bijzondere manier. Wanneer ze in de loop van de tijd in een grafiek worden weergegeven, neemt de golf die wordt getraceerd door deze spanning van wisselende polariteit van

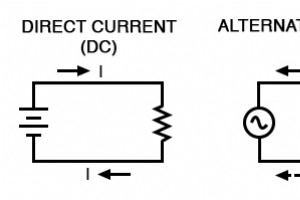
De meeste studenten elektriciteit beginnen hun studie met wat bekend staat als gelijkstroom (DC), wat elektriciteit is die in een constante richting stroomt en/of een spanning heeft met constante polariteit. DC is het soort elektriciteit dat wordt opgewekt door een batterij (met duidelijke positiev

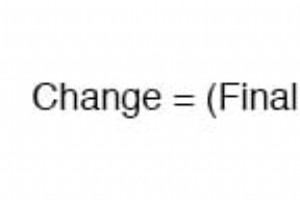
Soms is het nodig om de tijdsduur te bepalen die een reactief circuit nodig heeft om een ​​vooraf bepaalde waarde te bereiken. Dit geldt met name in gevallen waarin we een RC- of L/R-circuit ontwerpen om een ​​nauwkeurige timingfunctie uit te voeren. Om dit te berekenen, moeten we onze Universele ti

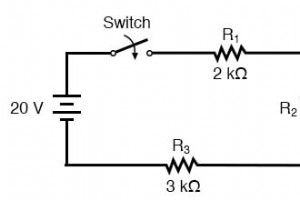
Wat doen we als we een circuit tegenkomen dat complexer is dan de eenvoudige serieconfiguraties die we tot nu toe hebben gezien? Neem dit circuit als voorbeeld: De eenvoudige tijdconstante-formule (τ=RC) is gebaseerd op een eenvoudige serieweerstand die op de condensator is aangesloten. Overi

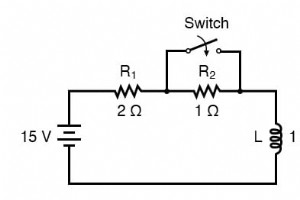
Er zijn omstandigheden waarin u mogelijk een DC-reactief circuit moet analyseren wanneer de startwaarden van spanning en stroom niet overeenkomen met een volledig ontladen toestand. Met andere woorden, de condensator kan beginnen in een gedeeltelijk geladen toestand in plaats van te beginnen bij nul

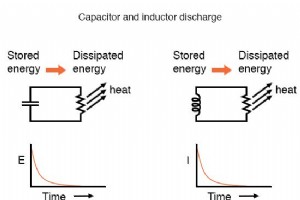
Meer informatie over L/R-tijdconstanten Het is vaak verbijsterend voor nieuwe studenten elektronica waarom de tijdconstante berekening voor een inductieve schakeling verschilt van die van een capacitieve schakeling. Voor een weerstand-condensatorcircuit wordt de tijdconstante (in seconden) berekend

Er is een zekere manier om een ​​van de waarden in een reactief DC-circuit in de loop van de tijd te berekenen. Waarden berekenen in een reactief gelijkstroomcircuit De eerste stap is om de begin- en eindwaarden te identificeren voor welke hoeveelheid de condensator of inductor zich tegen de verand