Enkele voorbeelden met wisselstroomcircuits

Laten we drie wisselspanningsbronnen in serie aansluiten en complexe getallen gebruiken om additieve spanningen te bepalen.

Alle regels en wetten die zijn geleerd in de studie van DC-circuits zijn ook van toepassing op AC-circuits (de wet van Ohm, de wetten van Kirchhoff, netwerkanalysemethoden), met uitzondering van vermogensberekeningen (de wet van Joule).

De enige kwalificatie is dat alle variabelen moeten worden uitgedrukt in complexe vorm, rekening houdend met fase en grootte, en alle spanningen en stromen moeten dezelfde frequentie hebben (zodat hun faserelaties constant blijven). (Figuur hieronder)

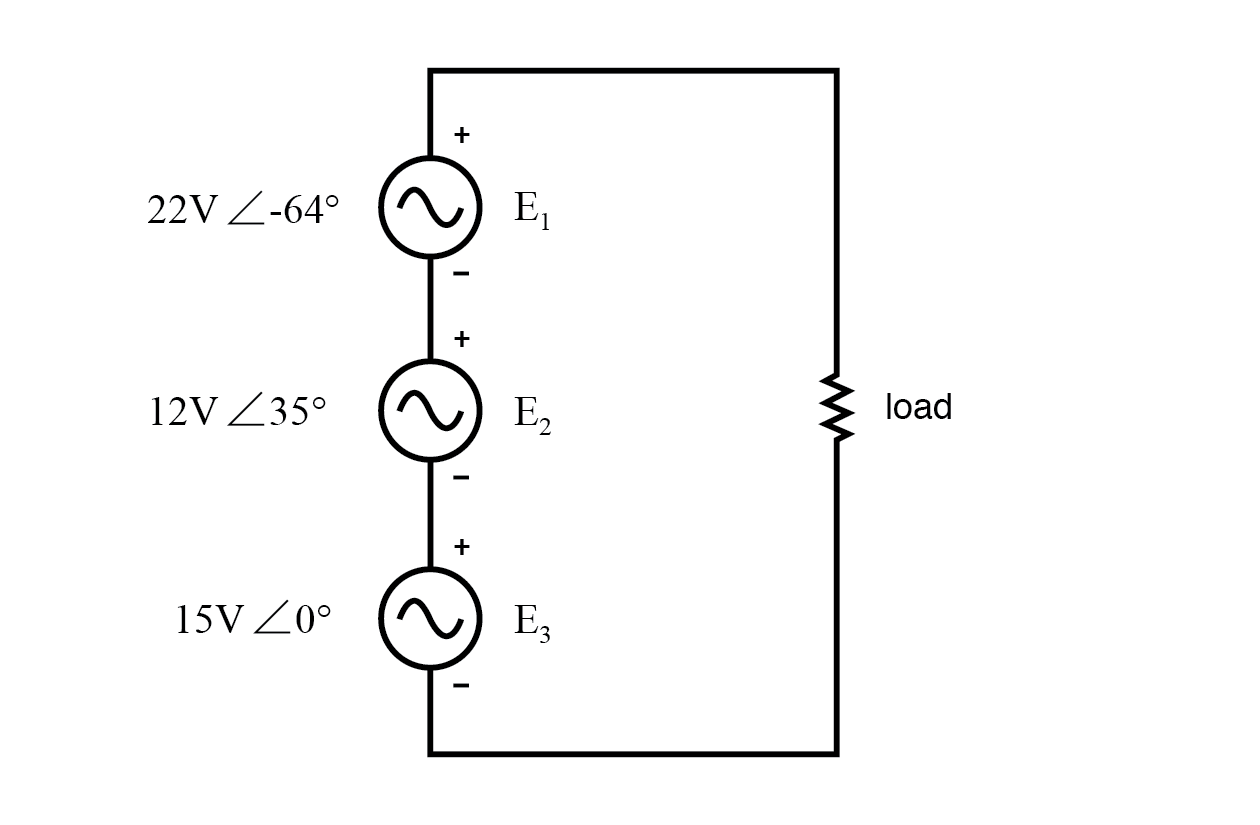
KVL staat de toevoeging van complexe spanningen toe.

De polariteitsmarkeringen voor alle drie de spanningsbronnen zijn zo georiënteerd dat hun aangegeven spanningen zouden moeten optellen om de totale spanning over de belastingsweerstand te maken.

Merk op dat hoewel grootte en fasehoek voor elke AC-spanningsbron worden gegeven, er geen frequentiewaarde is gespecificeerd. Als dit het geval is, wordt aangenomen dat alle frequenties gelijk zijn, waarmee we voldoen aan onze kwalificaties voor het toepassen van DC-regels op een AC-circuit (alle cijfers in de complexe vorm, allemaal met dezelfde frequentie).

De opzet van onze vergelijking om de totale spanning te vinden, ziet er als volgt uit:

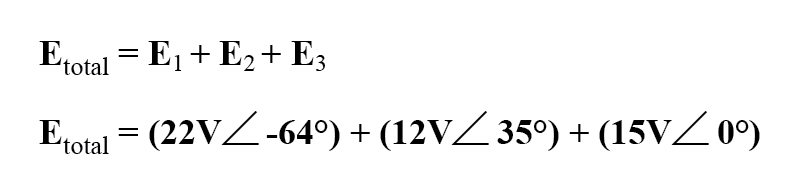
Grafisch tellen de vectoren op zoals weergegeven in onderstaande afbeelding.

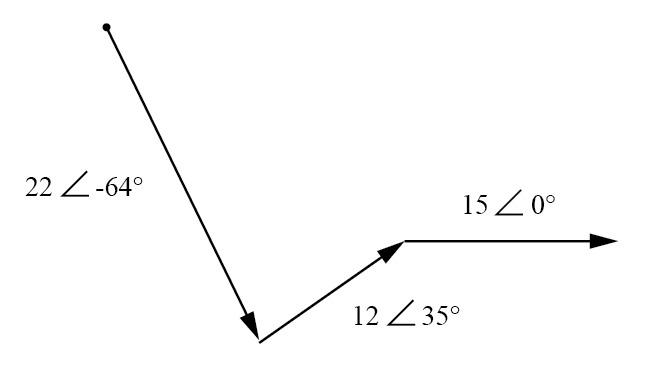
Grafische optelling van vectorspanningen.

De som van deze vectoren zal een resulterende vector zijn die begint bij het startpunt voor de 22-volt vector (de stip linksboven in het diagram) en eindigt bij het eindpunt voor de 15-volt vector (pijlpunt in het midden -rechts van het diagram):(Figuur hieronder)

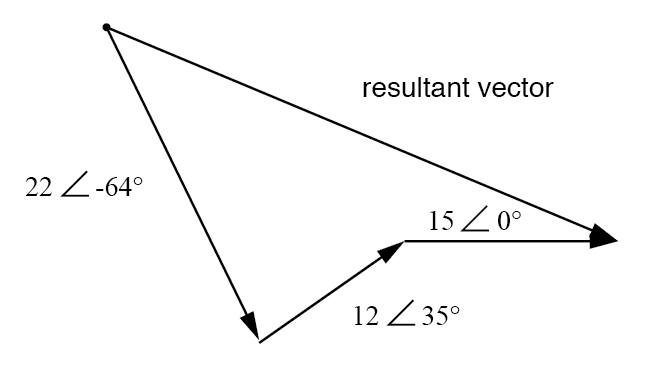
Resultaat is gelijk aan de vectorsom van de drie oorspronkelijke spanningen.

Om te bepalen wat de grootte en hoek van de resulterende vector zijn zonder toevlucht te nemen tot grafische afbeeldingen, kunnen we elk van deze complexe getallen in polaire vorm omzetten in een rechthoekige vorm en optellen.

Onthoud dat we toevoegen deze cijfers samen omdat de polariteitsmarkeringen voor de drie spanningsbronnen op een additieve manier zijn georiënteerd:

In polaire vorm komt dit overeen met 36,8052 volt ∠ -20,5018°. Wat dit in reële termen betekent, is dat de gemeten spanning over deze drie spanningsbronnen 36,8052 volt zal zijn, met een achterstand van 20,5018° op de 15 volt (0° fasereferentie).

Een voltmeter die over deze punten in een echt circuit is aangesloten, zou alleen de polaire grootte van de spanning (36,8052 volt) aangeven, niet de hoek. Een oscilloscoop kan worden gebruikt om twee spanningsgolfvormen weer te geven en zo een faseverschuivingsmeting te geven, maar geen voltmeter.

Hetzelfde principe geldt voor AC-ampèremeters:ze geven de polaire grootte van de stroom aan, niet de fasehoek.

Dit is uiterst belangrijk bij het relateren van berekende cijfers van spanning en stroom aan echte circuits.

Hoewel de rechthoekige notatie handig is voor optellen en aftrekken en inderdaad de laatste stap was in ons voorbeeldprobleem hier, is het niet erg toepasbaar op praktische metingen.

Rechthoekige figuren moeten worden geconverteerd naar polaire figuren (met name polaire grootte ) voordat ze kunnen worden gerelateerd aan werkelijke circuitmetingen.

We kunnen SPICE gebruiken om de nauwkeurigheid van onze resultaten te verifiëren. In dit testcircuit is de weerstandswaarde van 10 kΩ vrij willekeurig. Het is daar zodat SPICE geen open-circuitfout verklaart en de analyse afbreekt.

Ook is de keuze van frequenties voor de simulatie (60 Hz) vrij willekeurig, omdat weerstanden uniform reageren op alle frequenties van wisselspanning en -stroom. Er zijn andere componenten (met name condensatoren en inductoren) die niet uniform reageren op verschillende frequenties, maar dat is een ander onderwerp! (Figuur hieronder)

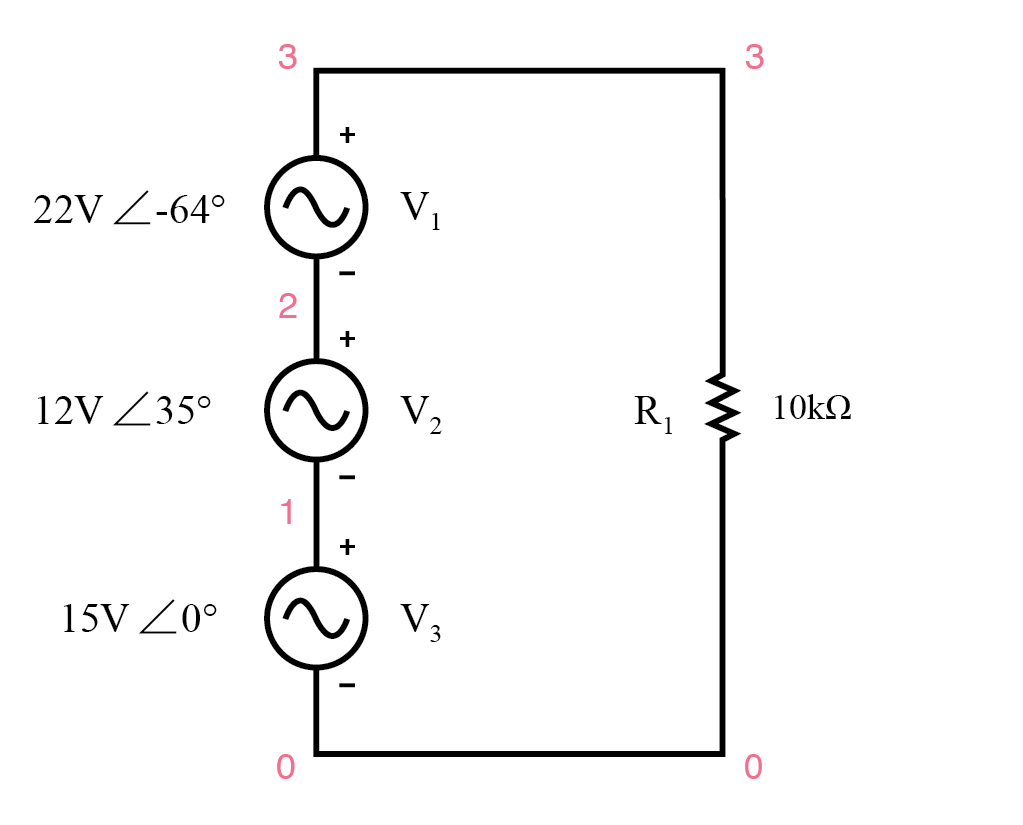
Schema van kruidencircuit.

v1 1 0 ac 15 0 sin v2 2 1 ac 12 35 sin v3 3 2 ac 22 -64 sin r1 3 0 10k .ac link 1 60 60 Ik gebruik een frequentie van 60 Hz .print ac v(3,0) vp(3,0) als standaardwaarde .einde freq v(3) vp(3) 6.000E+01 3.681E+01 -2.050E+01 

En ja hoor, we krijgen een totale spanning van 36,81 volt ∠ -20,5° (met verwijzing naar de 15 volt-bron, waarvan de fasehoek willekeurig op nul graden werd vermeld om de "referentie" -golfvorm te zijn).

Op het eerste gezicht is dit contra-intuïtief. Hoe is het mogelijk om een ​​totale spanning van iets meer dan 36 volt te krijgen met voedingen van 15 volt, 12 volt en 22 volt die in serie zijn geschakeld? Met DC zou dit onmogelijk zijn, omdat spanningscijfers ofwel direct worden opgeteld of afgetrokken, afhankelijk van de polariteit.

Maar met AC kan onze "polariteit" (faseverschuiving) overal variëren tussen volledige hulp en volledige tegenwerking, en dit maakt zo'n paradoxale optelling mogelijk.

Wat als we hetzelfde circuit zouden nemen en een van de aansluitingen van de voeding zouden omkeren? Zijn bijdrage aan de totale spanning zou dan het tegenovergestelde zijn van wat het was:(figuur hieronder)

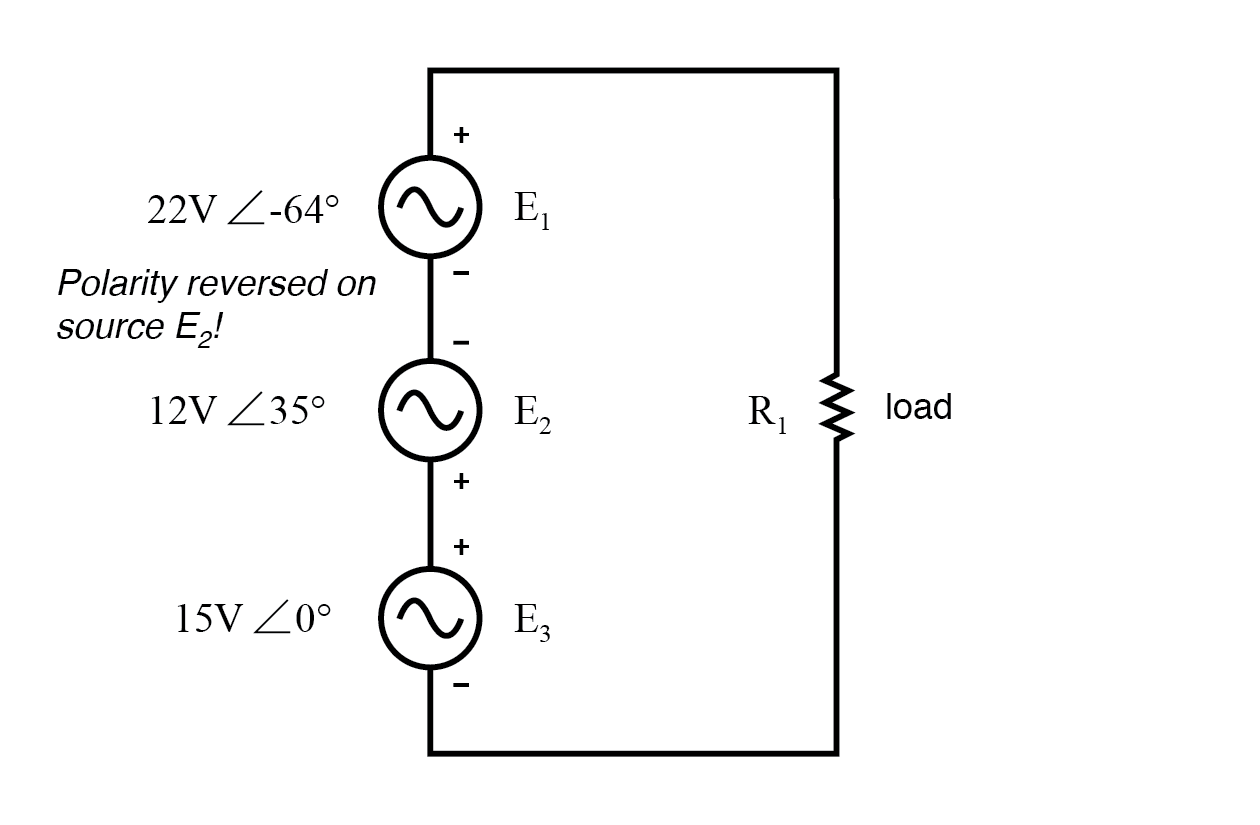
De polariteit van E₂ (12V) is omgekeerd.

Merk op hoe de fasehoek van de 12 volt-voeding nog steeds 35° wordt genoemd, ook al zijn de draden omgedraaid. Onthoud dat de fasehoek van een spanningsval wordt vermeld in verwijzing naar de aangegeven polariteit. Hoewel de hoek nog steeds wordt geschreven als 35°, wordt de vector 180° tegengesteld aan wat het voorheen was:(figuur hieronder)

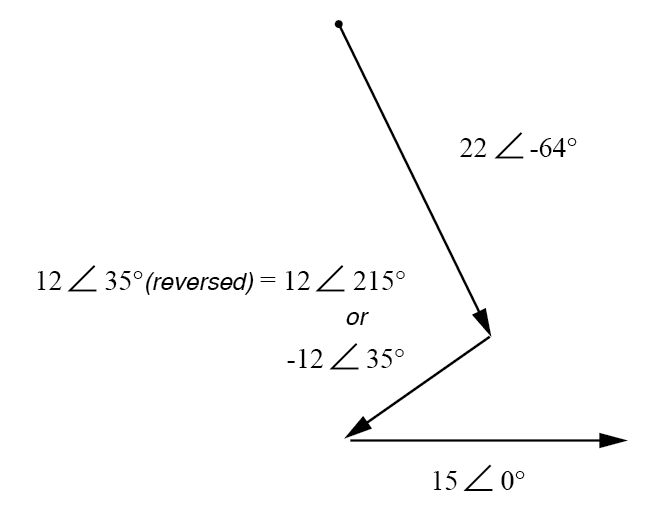
De richting van E₂ is omgekeerd.

De resulterende (som) vector moet beginnen op het punt linksboven (oorsprong van de 22-volt vector) en eindigen op de punt van de rechterpijl van de 15-volt vector:(figuur hieronder)

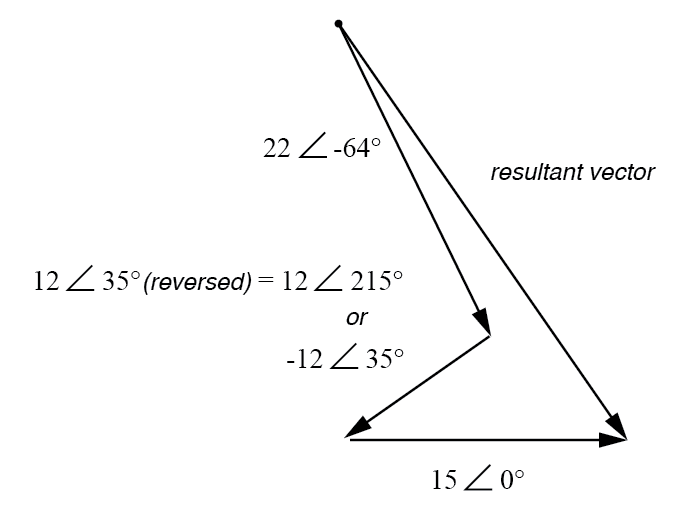
Resultaat is de vectorsom van spanningsbronnen.

De omkering van de verbinding op de 12 volt-voeding kan op twee verschillende manieren in polaire vorm worden weergegeven:door 180° op te tellen bij de vectorhoek (waardoor het 12 volt ∠ 215° wordt), of een omkering van het teken op de grootte (waardoor het - 12 volt ∠ 35°). Hoe dan ook, conversie naar rechthoekige vorm levert hetzelfde resultaat op:

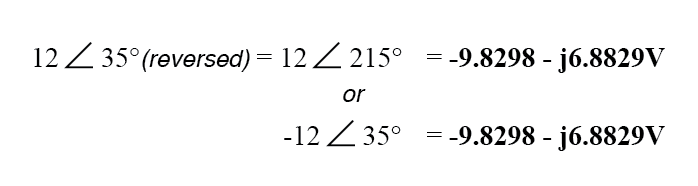
De resulterende optelling van spanningen in rechthoekige vorm, dan:

In polaire vorm komt dit overeen met 30,4964 V ∠ -60,9368°. Nogmaals, we zullen SPICE gebruiken om de resultaten van onze berekeningen te verifiëren:

wisselspanning toevoeging v1 1 0 ac 15 0 sin v2 1 2 ac 12 35 sin Let op de omkering van knooppuntnummers 2 en 1 v3 3 2 ac 22 -64 sin om het verwisselen van verbindingen te simuleren r1 3 0 10k .ac lin 1 60 60 .print ac v(3,0) vp(3,0) .einde freq v(3) vp(3) 6.000E+01 3.050E+01 -6.094E+01 

BEOORDELING:

• Alle wetten en regels van DC-circuits zijn van toepassing op AC-circuits, met uitzondering van vermogensberekeningen (de wet van Joule), zolang alle waarden in complexe vorm worden uitgedrukt en gemanipuleerd en alle spanningen en stromen dezelfde frequentie hebben .
• Bij het omkeren van de richting van een vector (gelijk aan het omkeren van de polariteit van een wisselspanningsbron ten opzichte van andere spanningsbronnen), kan dit op twee verschillende manieren worden uitgedrukt:180° aan de hoek toevoegen of de hoek omkeren teken van de grootte.
• Metermetingen in een wisselstroomcircuit komen overeen met de polaire grootheden van berekende waarden. Rechthoekige uitdrukkingen van complexe grootheden in een wisselstroomcircuit hebben geen direct, empirisch equivalent, hoewel ze handig zijn voor het uitvoeren van optellen en aftrekken, zoals de spannings- en stroomwetten van Kirchhoff vereisen.

GERELATEERDE WERKBLAD:

• Werkblad AC-netwerkanalyse
• Wetten van Kirchoff's werkblad
• Werkblad Wet van Ohm