Spannings- en stroomberekeningen

Er is een zekere manier om een ​​van de waarden in een reactief DC-circuit in de loop van de tijd te berekenen.

Waarden berekenen in een reactief gelijkstroomcircuit

De eerste stap is om de begin- en eindwaarden te identificeren voor welke hoeveelheid de condensator of inductor zich tegen de verandering verzet; dat wil zeggen, welke hoeveelheid de reactieve component ook probeert constant te houden. Voor condensatoren is deze hoeveelheid spanning; voor inductoren is deze hoeveelheid huidig . Wanneer de schakelaar in een circuit wordt gesloten (of geopend), zal de reactieve component proberen die hoeveelheid op hetzelfde niveau te houden als vóór de overgang van de schakelaar, zodat die waarde wordt gebruikt voor de "start" -waarde.

De uiteindelijke waarde voor deze hoeveelheid is wat die hoeveelheid ook zal zijn na een oneindige hoeveelheid tijd. Dit kan worden bepaald door een capacitief circuit te analyseren alsof de condensator een open circuit is, en een inductief circuit alsof de inductor een kortsluiting is, want dat is wat deze componenten doen alsof ze "volledig opgeladen" zijn. na een oneindige hoeveelheid tijd.

De volgende stap is het berekenen van de tijdconstante van het circuit:de hoeveelheid tijd die nodig is voordat spannings- of stroomwaarden ongeveer 63 procent veranderen van hun startwaarden naar hun uiteindelijke waarden in een tijdelijke situatie.

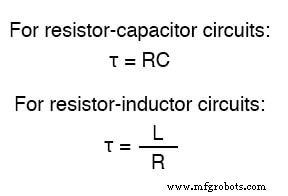
In een serie RC-schakeling is de tijdconstante gelijk aan de totale weerstand in ohm vermenigvuldigd met de totale capaciteit in farads. Voor een serie L/R-circuit is dit de totale inductantie in Henrys gedeeld door de totale weerstand in ohm. In beide gevallen wordt de tijdconstante uitgedrukt in eenheden van seconden en gesymboliseerd door de Griekse letter “tau” (τ):

De stijging en daling van circuitwaarden zoals spanning en stroom als reactie op een transiënt zijn, zoals eerder vermeld, asymptotisch . Als dat zo is, beginnen de waarden snel na de transiënt te veranderen en na verloop van tijd te stabiliseren. Indien uitgezet in een grafiek, vormt de benadering van de uiteindelijke waarden van spanning en stroom exponentiële curven.

Zoals eerder vermeld, is één tijdconstante de hoeveelheid tijd die een van deze waarden nodig heeft om ongeveer 63 procent te veranderen van hun beginwaarden naar hun (uiteindelijke) eindwaarden. Voor elke tijdconstante komen deze waarden (ongeveer) 63 procent dichter bij hun uiteindelijke doel. De wiskundige formule voor het bepalen van het precieze percentage is vrij eenvoudig:

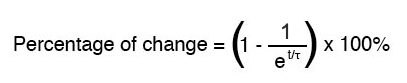
De letter e staat voor de constante van Euler, die ongeveer 2,7182818 is. Het is afgeleid van calculustechnieken, na mathematische analyse van de asymptotische benadering van de circuitwaarden. Na de tijdswaarde van een tijdconstante, is het veranderingspercentage van de beginwaarde naar de eindwaarde:

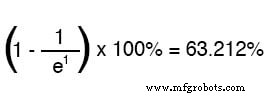
Na de tijdsduur van twee tijdconstanten, is het veranderingspercentage van beginwaarde naar eindwaarde:

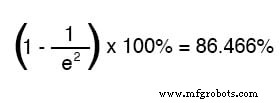
Na tien tijdconstanten aan tijd, is het percentage:

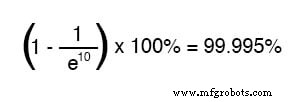
Hoe meer tijd er verstrijkt sinds de tijdelijke toepassing van spanning van de batterij, hoe groter de waarde van de noemer in de breuk, wat zorgt voor een kleinere waarde voor de hele breuk, wat zorgt voor een totaal (1 minus de breuk) die nadert 1, of 100 procent.

Universele tijdconstante formule

We kunnen hier een meer universele formule van maken voor de bepaling van spannings- en stroomwaarden in tijdelijke circuits, door deze hoeveelheid te vermenigvuldigen met het verschil tussen de uiteindelijke en startcircuitwaarden:

Laten we de spanningsstijging op het serieweerstand-condensatorcircuit analyseren dat aan het begin van het hoofdstuk wordt getoond.

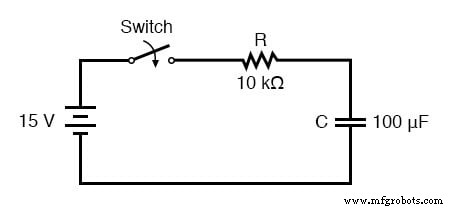
Merk op dat we ervoor kiezen om de spanning te analyseren, omdat dat de hoeveelheid condensatoren is die de neiging hebben om constant te blijven. Hoewel de formule redelijk goed werkt voor stroom, worden de begin- en eindwaarden voor stroom eigenlijk afgeleid van de spanning van de condensator, dus de berekeningsspanning is een meer directe methode. De weerstand is 10 kΩ en de capaciteit is 100 µF (microfarads). Aangezien de tijdconstante (τ) voor een RC-circuit het product is van weerstand en capaciteit, verkrijgen we een waarde van 1 seconde:

Als de condensator start in een volledig ontladen toestand (0 volt), dan kunnen we die spanningswaarde gebruiken voor een "start" -waarde. De uiteindelijke waarde is natuurlijk de accuspanning (15 volt). Onze universele formule voor condensatorspanning in dit circuit ziet er als volgt uit:

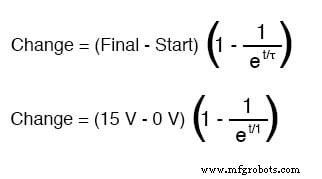
Dus, na 7,25 seconden van het aanleggen van een spanning via de gesloten schakelaar, zal onze condensatorspanning zijn toegenomen met:

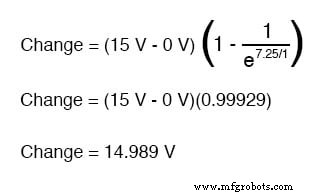
Aangezien we begonnen met een condensatorspanning van 0 volt, betekent deze toename van 14,989 volt dat we na 7,25 seconden 14,989 volt hebben.

Dezelfde formule zal ook werken om de stroom in dat circuit te bepalen. Omdat we weten dat een ontladen condensator in eerste instantie werkt als een kortsluiting, zal de startstroom het maximaal mogelijke zijn:15 volt (van de batterij) gedeeld door 10 kΩ (de enige oppositie tegen stroom in het circuit aan het begin):

We weten ook dat de eindstroom nul zal zijn, omdat de condensator zich uiteindelijk zal gedragen als een open circuit, wat betekent dat er uiteindelijk geen elektronen in het circuit zullen stromen. Nu we zowel de start- als de eindstroomwaarden kennen, kunnen we onze universele formule gebruiken om de stroom te bepalen na 7,25 seconden schakelaarsluiting in hetzelfde RC-circuit:

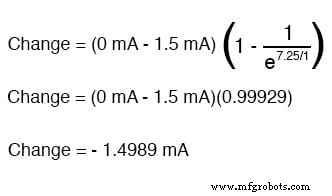
Merk op dat het verkregen cijfer voor verandering negatief is, niet positief! Dit vertelt ons dat de stroom is afgenomen in plaats van met het verstrijken van de tijd toe te nemen. Aangezien we begonnen met een stroomsterkte van 1,5 mA, betekent deze afname (-1,4989 mA) dat we na 7,25 seconden 0,001065 mA (1,065 µA) hebben.

We hadden ook de circuitstroom op tijd =7,25 seconden kunnen bepalen door de spanning van de condensator (14,989 volt) af te trekken van de spanning van de batterij (15 volt) om de spanningsval over de 10 kΩ-weerstand te verkrijgen, en vervolgens de stroom door de weerstand (en de hele serieschakeling) met de wet van Ohm (I=E/R). Hoe dan ook, we zouden hetzelfde antwoord moeten krijgen:

De universele tijdconstante-formule gebruiken voor het analyseren van inductieve circuits

De universele tijdconstante-formule werkt ook goed voor het analyseren van inductieve circuits. Laten we het toepassen op ons voorbeeld L/R-circuit aan het begin van het hoofdstuk:

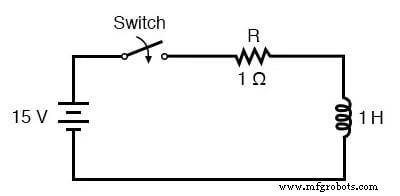
Met een inductantie van 1 henry en een serieweerstand van 1 is onze tijdconstante gelijk aan 1 seconde:

Omdat dit een inductief circuit is en we weten dat inductoren zich verzetten tegen de verandering in stroom, zullen we onze tijdconstante-formule opstellen voor begin- en eindwaarden van stroom. Als we beginnen met de schakelaar in de open positie, is de stroom gelijk aan nul, dus nul is onze startstroomwaarde.

Nadat de schakelaar lange tijd gesloten is gelaten, zal de stroom naar zijn eindwaarde afzakken, gelijk aan de bronspanning gedeeld door de totale circuitweerstand (I=E/R), of 15 ampère in het geval van dit circuit .

Als we de waarde van stroom op 3,5 seconden zouden willen bepalen, zouden we de universele tijdconstante-formule als zodanig toepassen:

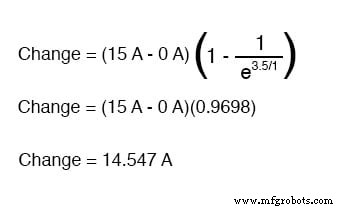
Gezien het feit dat onze startstroom nul was, blijven we op een circuitstroom van 14.547 ampère op 3,5 seconden tijd.

Het bepalen van de spanning in een inductief circuit kan het beste worden bereikt door eerst de circuitstroom te berekenen en vervolgens de spanningsdalingen over weerstanden te berekenen om te bepalen wat er nog over de inductor valt. Met slechts één weerstand in ons voorbeeldcircuit (met een waarde van 1 Ω), is dit vrij eenvoudig:

Afgetrokken van onze batterijspanning van 15 volt, blijft er 0,453 volt over de spoel op tijd =3,5 seconden.

BEOORDELING:

• Universele tijdconstante formule:
• Volg deze stappen om een ​​RC- of L/R-circuit te analyseren:
• (1):Bepaal de tijdconstante voor het circuit (RC of L/R).
• (2):Identificeer de te berekenen hoeveelheid (welke hoeveelheid dan ook waarvan de verandering direct wordt tegengewerkt door de reactieve component. Voor condensatoren is dit spanning; voor inductoren is dit stroom).
• (3):Bepaal de begin- en eindwaarden voor die hoeveelheid.
• (4):Sluit al deze waarden (Final, Start, tijd, tijdconstante) aan op de universele tijdconstante-formule en los op voor verandering in hoeveelheid.
• (5):Als de startwaarde nul was, dan is de werkelijke waarde op het opgegeven tijdstip gelijk aan de berekende verandering gegeven door de universele formule. Als dat niet het geval is, voegt u de wijziging toe aan de startwaarde om erachter te komen waar u zich bevindt.

GERELATEERDE WERKBLAD:

• Werkblad Tijdconstante circuits
• Werkblad Tijdconstante Berekeningen

Bekijk onze collectie Krachtcalculators in onze Hulpprogramma's sectie.