Multifunctioneel grafeenmeta-oppervlak om vortexgolven te genereren en te sturen

Methoden

De geleidbaarheid van grafeen bestaat uit interband en intraband overgang. De intrabandovergang domineert het terahertz- en infraroodregime, terwijl de interbandovergang het zichtbare optische regime domineert. In terahertz en infrarood kan de geleidbaarheid worden gemodelleerd door Drude model [24],

waar k _B is Boltzmann-constante, T is de temperatuur, τ is de ontspanningstijd, en E _f is Fermi-energie.

In dit werk werkt het apparaat in het terahertz-regime, waar E _f ≫k _B T; daarom kan de vergelijking worden vereenvoudigd als

uitgaande van de typische waarde van kamertemperatuur T =300K , en de relaxatietijd van grafeen τ =1 st. In dit werk wordt de Fermi-energie E _f wordt geregeld door externe statische poortspanning. In de simulatie wordt grafeen niet gemodelleerd als 3D-metamateriaalblokken, maar als 2D-oppervlaktegeleidende omstandigheden vanwege de atomaire dikte.

Het meta-oppervlak van grafeen is samengesteld uit een groot aantal grafeencellen, wat resulteert in collectief plasmonisch gedrag dat op het oppervlak wordt geëxciteerd, waardoor buitengewone elektromagnetische eigenschappen worden gerealiseerd. De frequentie is 1,3 THz; dus, vanwege de langzame golfvoortplanting geassocieerd met de plasmonische modus, kan de resonantie optreden bij zeer kleine afmetingen, d.w.z. e., onder λ /10 [23, 42]. Om het meta-oppervlak van grafeencellen te ontwerpen, wordt een kalibratiegrafiek van het reflectieve gedrag van een grafeencel geëxtraheerd om de gedetailleerde invloed van elke parameter in een enkele grafeencel te bestuderen.

Een typische eenheidsgrafeencel, zoals weergegeven in figuur 1, is samengesteld uit een meerlagige structuur met een grafeenpatch van atomaire dikte aan de bovenkant gemonteerd. De grafeen patch met een grootte van w _x ×w _j wordt in het midden gemonteerd op een stapel gelaagde vierkante substraten met zijlengtes p van 14 µm. Een kwartssubstraat (ε _r =3.75,tanδ =0,0184) met een dikte van 25 µm wordt bovenop de metalen grondlaag onderaan geplaatst. Een externe voorspanning wordt aangelegd tussen de grafeenpatch en een polykristallijne siliciumlaag met een dikte van 50 nm. Een 10 nm dikke Al₂ O₃ (Aluinaarde, \(\epsilon _{r}=8.9, \tan \delta =0.01\)) laag wordt tussengevoegd als spacer. De chemische potentiaal kan worden aangepast van 0,01 tot 1,0 eV, door de door externe voorspanning te regelen DC-spanning van 0 tot 14,7 V [23, 35]. Er moet worden vermeld dat de polykristallijne siliciumlaag en de aluminiumoxide-afstandhouder niet zijn gemodelleerd in de simulatie in dit artikel en de redenen zijn als volgt. Ten eerste wordt een aparte 2D-simulatie uitgevoerd, die veel goedkoper is, om aan te tonen dat, aangezien de dikte van de polykristallijne siliciumlaag en de Alumina-spacer veel kleiner is dan die van het kwartssubstraat, hun invloed op het reflectiegedrag kan worden verwaarloosd. Aan de andere kant is in de eindige-elementensimulaties een extreem aantal elementen vereist bij het omgaan met aangrenzende objecten met een enorm verschil in grootte. Als gevolg hiervan zullen 3D-simulaties die deze twee lagen modelleren extreem duur zijn.

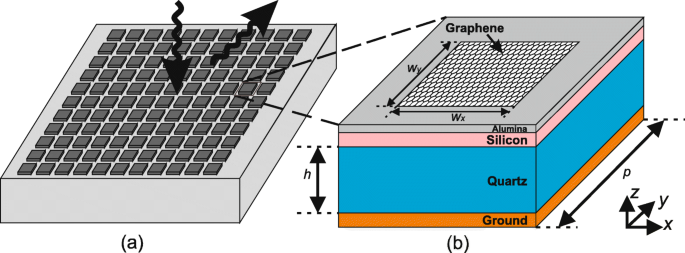
Illustratie van grafeenmetasurface en celconfiguratie. een Schematische voorstelling van een meta-oppervlak van grafeen, dat de inkomende elektromagnetische golven kan sturen door abnormale reflectie. b Configuratie van een grafeencel, die bestaat uit een meerlagig substraat en een gemonteerde grafeenpatch van de grootte w _x ×w _j . Een statische poortspanning wordt aangelegd tussen de grafeenpatch en de siliciumlaag om de chemische potentiaal te regelen

Om de reflecterende eigenschappen te bestuderen die worden beïnvloed door μ _c en w _x , worden periodieke voorwaarden toegewezen in zowel x en y routebeschrijving. De golf valt normaal van bovenaf met parallelle polarisatie, d.w.z. elektrisch veld gepolariseerd in x -richting. Aangezien grafeen equivalent is aan complexe oppervlaktegeleiding, alleen w _x kan de geleiding in x . beïnvloeden -richting aanzienlijk, terwijl w _j heeft een verwaarloosbare invloed en is vastgesteld op 4 µm in alle simulaties in dit artikel.

Om de invloeden van patchgrootte en chemisch potentieel nauwkeurig te onderzoeken, vegen we w _x van 0,2 tot 13,8 µm in stappen van 0,2 µm, en veeg μ _c van 0,01 tot 1,00 eV in stappen van 0,01 eV, en de frequentie is vastgesteld op 1,3 THz. De fase en grootte van S ₁₁ zijn uitgezet in Fig. 2, die de kalibratiegrafieken worden genoemd omdat de waarde van w _x en μ _c kan van hen worden gekalibreerd. Om de efficiëntie van het meta-oppervlak te garanderen, moet de grootte van de reflectiecoëfficiënt groter zijn dan 0,7; dus de niet-gekwalificeerde regio's worden als blanco uitgegraven. In de kalibratiegrafiek krijgt men een volledige dekking van 360 ^∘ wat voldoende is om grafeenmeta-oppervlakken te construeren.

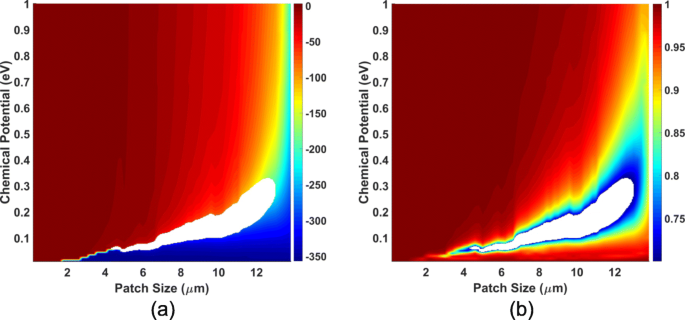
Kalibratiediagram van reflectiecoëfficiënten van de grafeencel. De reflectiecoëfficiënt van de grafeencel beïnvloed door de grootte van de grafeenpatch w _x en het chemische potentieel μ _c , waarbij het gebied waar de reflectie kleiner is dan 0,7 wordt afgetrokken. een fase en b magnitude diagram

Het fasediagram moet soepel genoeg zijn om de fase nauwkeurig te regelen. Om de parameters van grafeencellen te ontwerpen om volledige fasedekking te bereiken vanaf 0 ^∘ tot 360 ^∘ , zeven combinaties van w _x en μ _c zijn geselecteerd, zoals weergegeven in Fig. 3.

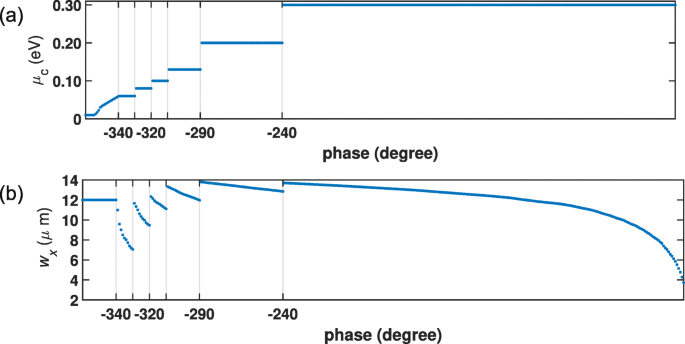
Ontwerpdiagram van grafeencel. Een volledige 360 ^∘ fasedekking bereikt door zeven groepen combinaties van a chemisch potentieel en b patchgrootte

Resultaten en discussies

Om verschillende functies te realiseren, zou het erg handig zijn om de functionaliteiten van twee meta-oppervlakken te combineren, of nieuwe functies toe te voegen aan een andere. Deze methodologie biedt een veelzijdige manier om nieuwe meta-oppervlakken te ontwerpen. We combineren de functionaliteiten van het genereren van vortexgolven en golfafbuiging door abnormale reflectie in dit artikel.

Hieronder wordt een algemene methodologie voorgesteld om twee meta-oppervlakken te combineren MS₁ en MS₂ in één multifunctioneel meta-oppervlak MS_t . Om de combinatie te realiseren, beginnen we met de algemene wet van reflectie [25]. Overweeg, zoals geïllustreerd in Fig. 4, een vlakke golf met een vrije-ruimtegolflengte λ botst met invalshoek θ _ik , de volgende vergelijking beschrijft de algemene wet van reflectie,

$$ \sin\theta_{r}-\sin\theta_{i}=\frac{\lambda}{2\pi n_{i}}\frac{\,\mathrm{d}\phi}{\text{ dx}}, $$ (1)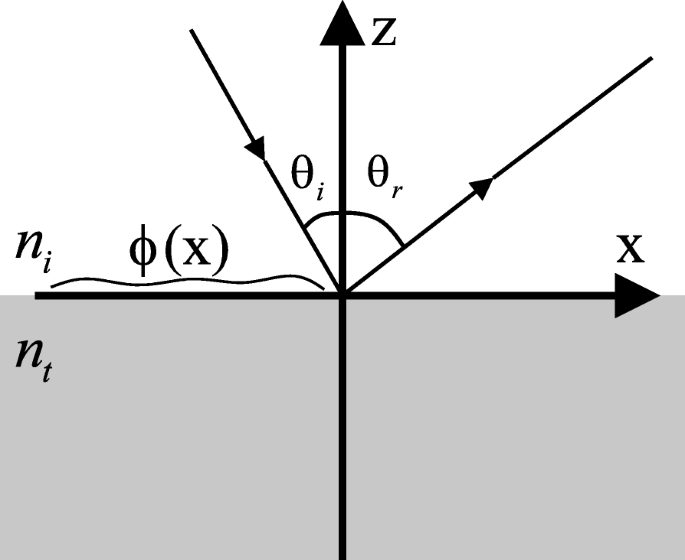

Illustratie van gegeneraliseerde wet van reflectie. Een elektromagnetische golf botst van bovenaf op de invallende engel θ _ik , terwijl wordt weergegeven door θ _r anders dan θ _ik , vanwege faseonderbreking ϕ (x ) langs de interface

waar θ _r is de reflectiehoek, n _ik is de brekingsindex in de bovenste ruimte, en ϕ (x ) beschrijft de fasediscontinuïteit langs de interface.

Beschouw het vereenvoudigde geval dat de golf normaal inslaat, en de bovenste ruimte is vrije ruimte (n _ik =1), zoals weergegeven in Fig. 5, voor de eerste twee meta-oppervlakken MS₁ en MS₂ , Verg. 1 kan verder worden vereenvoudigd als

$$ \frac{\,\mathrm{d} \phi_{m}}{\text{dx}}=\frac{2\pi}{\lambda}\sin\theta_{rm}(x)\quad\ quad m=1,2. $$ (2)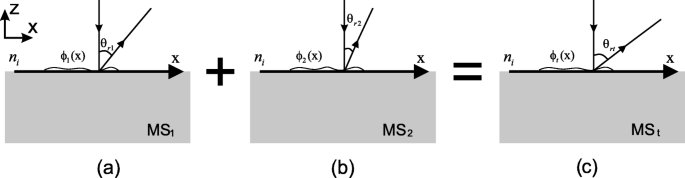

Illustratie van het combineren van twee meta-oppervlakken tot één multifunctioneel meta-oppervlak. In de inzet vallen de elektromagnetische golven normaal vanuit de bovenste ruimte met brekingsindex n _ik . een Metasruface 1 (MS₁ ) met faseonderbreking ϕ ₁ (x ) en b metasurface 2 (MS₂ ) met faseonderbreking ϕ ₂ (x ) worden gecombineerd tot c het gewenste multifunctionele meta-oppervlak (MS_t ) met faseonderbreking ϕ _t (x ). θ _{r 1} (x ), θ _{r 2} (x ) en θ _rt (x ) zijn respectievelijk de hoeken van afwijkende reflectie langs de grensvlakken van de meta-oppervlakken, en de relatie θ _rt (x )=θ _{r 1} (x )+θ _{r 2} (x ) geldt overal in MS_t

Om ϕ . te verkrijgen _t van MS_t , we kiezen een segment D _x langs de interface, en het probleem wordt het volgende:neem aan in x ∈D _x , houdt −π . vast /2<θ _{r 1} (x )+θ _{r 2} (x )<π /2, zoek ϕ _t , s. t. voor ∀x ∈D _x , dat

$$ \begin{aligned} \frac{\,\mathrm{d}\phi_{t}}{\text{dx}}&=\frac{2\pi}{\lambda}\sin\theta_{rt} ,\quad \text{en}\\ \theta_{rt}(x)&=\theta_{r1}(x)+\theta_{r2}(x). \end{uitgelijnd} $$ (3)

Het kan worden afgeleid van Vgl. 2 en 3 dat

$$ \begin{aligned} \frac{\,\mathrm{d} \phi_{t}}{\text{dx}} &=\frac{2\pi}{\lambda}\sin\theta_{rt} =\frac{2\pi}{\lambda}\sin(\theta_{r1}+\theta_{r2})\\ &=\frac{2\pi}{\lambda}\left(\cos\theta_{ r2}\sin\theta_{r1}+\cos\theta_{r1}\sin\theta_{r2}\right)\\ &=\cos\theta_{r2}\frac{\,\mathrm{d} \phi_ {1}}{\text{dx}}+\cos\theta_{r1}\frac{\,\mathrm{d} \phi_{2}}{\text{dx}}\\ &=\frac{\ ,\mathrm{d}}{\text{dx}}\left(\cos\theta_{r2}\phi_{1}+\cos\theta_{r1}\phi_{2}\right)\\ &\quad -\left(\sin\theta_{r2}\frac{\,\mathrm{d} \theta_{r2}}{\text{dx}}\phi_{1}+\sin\theta_{r1}\frac{ \,\mathrm{d} \theta_{r1}}{\text{dx}}\phi_{2}\right), \end{aligned} $$ (4)

wat leidt tot

$$ \begin{aligned} \phi_{t}(x)=&\cos\theta_{r2}\phi_{1}(x)+\cos\theta_{r1}\phi_{2}(x)\\ &-\int_{D_{x}}\left(\sin\theta_{r2}\frac{\,\mathrm{d} \theta_{r2}}{\text{dx}}\phi_{1}+\ sin\theta_{r1}\frac{\,\mathrm{d} \theta_{r1}}{\text{dx}}\phi_{2}\right)\text{dx}, \end{aligned} $$ (5)

waarbij de integratieterm de bijdrage van de variantie van θ . berekent _ri (x ) en kan meestal numeriek worden berekend. Vergelijking 5 speelt een cruciale rol om de functionaliteiten van twee meta-oppervlakken te combineren.

Bovendien, als de stuurhoek constant is, is de integratieterm in Vgl. 6 verdwijnt. Vergelijking 5 kan aanzienlijk worden vereenvoudigd als

$$ \phi_{t}(x)=\cos\theta_{r2}\phi_{1}(x)+\cos\theta_{r1}\phi_{2}(x)+C. $$ (6)

Dit is de leidende vergelijking om meta-oppervlakken te combineren, en de faseverdeling kan worden berekend om het genereren van wervelgolven en abnormale reflectie te combineren.

In dit artikel, MS₁ is het meta-oppervlak dat vortexgolven genereert, terwijl MS₂ is het meta-oppervlak dat de golven stuurt.

Zoals geïllustreerd in [35], vortexgolven met modus l kan worden gegenereerd door een plaat van N sectoren met opeenvolgende toename van faseverschuiving. De faseverschuiving van de n de sector ϕ _n kan worden berekend als ϕ _n =ϕ ₀ +2π n ik /N , waar ϕ ₀ is de faseverschuiving van de initiële sector. Bovendien moet, om een ​​vortexgolf te genereren, worden voldaan dat −N /2<l <N /2. Daarom, N =4 is voldoende om modi te genereren l =0, ±1.

Een vortexgolf genereren met l =1, is de plaat onderverdeeld in vier sectoren zoals weergegeven in figuur 6a. De fasevoorwaarde ϕ ₁ (x ,j ) is een stuksgewijs constante functie die met 90 ^∘ . afneemt door sectoren, tegen de klok in.

$$ \phi_{1}(x,y)=\left\{ \begin{aligned} &0^{\circ} &\quad &x\geq 0, y\geq 0\\ &-90^{\circ } &\quad &x<0, y\geq 0\\ &-180^{\circ} &\quad &x<0, y<0 \\ &-270^{\circ} &\quad &x\ geq0, y<0 \end{uitgelijnd} \rechts. $$ (7)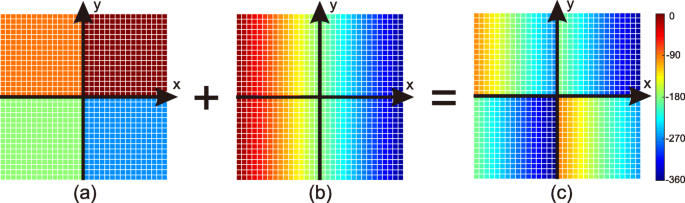

Illustratie van combinatie van fasediscontinuïteitsfuncties. een ϕ ₁ , fasediscontinuïteitsdistributie van MS₁ , die elektromagnetische vortexgolven genereert met l =1. b ϕ ₂ , fasediscontinuïteitsdistributie van MS₂ , wat resulteert in afwijkende reflectie. c Distributie van gecombineerde fasediscontinuïteit van de MS_t berekend door Vgl. 6

Wanneer x -gepolariseerde golf valt normaal van bovenaf in, vortexgolf met l =1 wordt weergegeven. Opgemerkt moet worden dat de golf verticaal wordt gereflecteerd; daarom is de afbuighoek 0 ^∘ , d.w.z. θ _{r 1} (x )=0 ^∘ .

Om afwijkende reflectie te genereren met een afbuighoek θ _r , Verg. 1 wordt toegepast. Zoals geïllustreerd in Fig. 4, wanneer de golf normaal in de vrije ruimte valt, d.w.z. θ _ik =0 ^∘ en n _ik =1, Vgl. 1 wordt teruggebracht tot

$$ \phi_{2}(x)=\frac{2\pi\sin\theta_{r}}{\lambda}x+C. $$

In dit werk is de afbuighoek ingesteld als θ _r =30 ^∘ . Uit de bovenstaande vergelijking, door te weten dat de periode van de eenheidscel 14 µm is, wordt het verschil in faseverschuiving tussen aangrenzende vlakken berekend als 10,9 ^∘ . De faseverdeling wordt getoond in Fig. 6b.

MS₁ combineren en MS₂ , we nemen θ _{r 1} (x )=0 ^∘ en θ _{r 2} (x )=30 ^∘ in Verg. 6 en verkrijg de ontwerpformule van MS_t ,

$$ \phi_{t}(x)=\frac{\sqrt{3}}{2}\phi_{1}(x)+\phi_{2}(x)+C. $$

Uit deze formule kan men de faseverdeling berekenen, die wordt getoond in figuur 6c. Volgens Fig. 3, door de chemische potentialen μ . te kiezen _c en de patchgrootte w _x van elke cel is een 32 × 32 grafeenmeta-oppervlak geconfigureerd. Figuur 1a toont het bovenaanzicht van de plaatsing van de grafeencellen op het metaoppervlak. Je kunt zien dat elke sector een subdomein van 16 × 16 is, met verticaal 16 kolommen. En elke kolom bestaat uit 16 identieke grafeenpatches, waarbij een bepaalde combinatie van w _x en μ _c is toegewezen.

De plaat wordt aangeslagen door een x -gepolariseerde golf die van bovenaf invalt. Het elektrische veld van de invallende golf is genormaliseerd, d.w.z. \( \vec {\mathrm {E}}_{\text {inc}}=\vec {x}\). De simulatie werd uitgevoerd met behulp van de commerciële eindige-elementenoplosser COMSOL Multiphysics 5.2. Grafeen heeft atomaire dikte; de dikte van de substraten is echter op micrometerschaal. Daarom zou de rekeninspanning enorm zijn als driedimensionale meshing wordt toegepast op grafeenpatches. Daarom wordt de dikte van de grafeenpatches genegeerd en wordt een equivalente tweedimensionale oppervlaktegeleidbaarheidsvoorwaarde toegepast als overgangsrandvoorwaarden in COMSOL Multiphysics. Er zijn 32×32 patches op de plaat, die is onderverdeeld in vier sectoren. Op elke sector zijn er 16 × 16-patches die onafhankelijk worden bestuurd op basis van hun grootte en chemisch potentieel. De simulatie verbruikte 7,1 miljoen vrijheidsgraden, die werd uitgevoerd op een server van 40 × 2,1 GHz-threads en 256 GB geheugen.

Figuur 7b toont de grootte van het elektrische veld van de gereflecteerde golf genormaliseerd door de invallende golf. Het meta-oppervlak van grafeen genereert een vortexgolf met l =1 en buigt af met 30 ^∘ richting x -as.

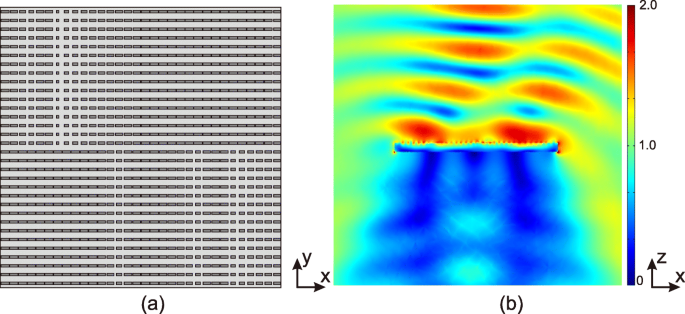
Resultaten van het multifunctionele meta-oppervlak. een Configuratie van de plaat met grafeenreflectarray bestaande uit 36 ​​× 36 grafeenpatches. De breedtes (w _j ) van alle grafeenpleisters worden genomen als 4 µm, en waarden van w _x worden geselecteerd om de fasediscontinuïteitstoestand te realiseren zoals weergegeven in Fig. 6. b De grootte van het elektrische veld van de gereflecteerde vortexgolf van l =1. De invallende golf is een x -gepolariseerde elektromagnetische golf met genormaliseerd elektrisch veld, normaal invallend vanaf de bovenkant. De golf wordt afgebogen met 30 ^∘ richting x -richting

Conclusies

Samenvattend hebben we het ontwerpprincipe van multifunctionele grafeenmeta-oppervlakken bestudeerd. De methodologie van het combineren van twee meta-oppervlakken wordt voorgesteld. Een meta-oppervlak van grafeen is bijvoorbeeld ontworpen om de functionaliteit van het genereren van vortexgolven en het sturen van de golven te combineren. Grafeen is een tweedimensionaal atomair dik materiaal dat de faseconditie dynamisch kan afstemmen door externe poortspanningen toe te passen. De parameters worden nauwkeurig onderzocht om het reflectieve gedrag van een enkele grafeencel te kalibreren en een dekking van 360 ^∘ te verkrijgen faseverschuiving. Een grafeenmeta-oppervlak bestaande uit 32 × 32 eenheidscellen is ontworpen om abnormale reflectie te realiseren en tegelijkertijd een vortex THz-golf te genereren. Simulatieresultaten laten zien dat een vortexgolf met l =1 wordt gegenereerd en gestuurd. Grafeen vertoont veel buitengewoon gedrag in het terahertz-regime, zoals het ondersteunen van SPP, hoge efficiëntie en afstembaarheid; daarom is het een veelbelovende kandidaat in terahertz-technologie. Dit onderzoek onderzoekt de benadering om de functionaliteiten van verschillende meta-oppervlakken te combineren, geïmplementeerd door grafeen, wat de poort opent naar dynamisch gecontroleerde multifunctionele meta-oppervlakken in het terahertz-regime.

Beschikbaarheid van gegevens en materialen

De datasets die zijn gegenereerd tijdens en/of geanalyseerd tijdens het huidige onderzoek zijn op redelijk verzoek verkrijgbaar bij de corresponderende auteurs.

Afkortingen

OAM:

Orbitaal impulsmoment

SPP:

Oppervlakteplasmonpolariton