Longitudinale elektromagnetische oscillaties in metalen: Oppervlakte-excitatiën op vlakke en spherische interfaces

Samenvatting

De gangbare definitie van de ruimtelijk-dispersieve permittiviteit wordt herzien. De respons van het gedegeneerde elektrongas op een elektrisch veld dat de vector-Helmholtz-vergelijking voldoet, wordt gevonden met een oplossing van de Boltzmann-vergelijking. De berekende longitudinale diëlektrische functie komt overeen met die verkregen door Klimontovich en Silin in 1952 en Lindhard in 1954. Echter, het hangt af van het kwadraat van het golgetal, een parameter van de vector-Helmholtz-vergelijking, maar niet de golfvector van een vlakke elektromagnetische golf. Dit nieuwe concept vereenvoudigt simulatie van niet-lokale effecten, bijvoorbeeld met een gegeneraliseerde Lorents-Mie-theorie, aangezien geen Fourier-transformaties nodig zijn. De Fresnel-coëfficiënten worden gegeneraliseerd ten einde excitatie van longitudinale elektromagnetische golven toe te laten. Om de theorie te verifiëren, worden de extinctiespectra voor zilver en goud nanometer-grote spheren berekend. Voor deze deeltjes geeft de gegeneraliseerde Lorents-Mie-theorie de blauwverschuiving en verbreeding van de plasmon-resonantie die in uitstekende overeenstemming zijn met experimentele data. Daarnaast verklaart de niet-lokale theorie het verdwijnen van de plasmon-resonantie waargenomen voor goudspheren met diameters kleiner dan of gelijk aan 2 nm. De berekeningen met de Klimontovich-Silin-Lindhard en hydrodynamische diëlektrische functies voor zilver geven nauwkeurige resultaten bij fotonenergieën van 3 tot 4 eV. We tonen aan dat de absolute waarden van de golgetallen van de longitudinale golven in vastestoffen veel hoger zijn dan die van de transversale golven.

Achtergrond

Bestraling van een vlak metaaloppervlak door femtoseconde laserpulsen resulteert vaak in de vorming van laser-geïnduceerde periodieke oppervlaktestructuren (LIPSS). Naast de LIPSS werden hyperfijne rimpels genaamd high-spatial-frequency LIPSS (HSFL) waargenomen. De ruimtelijke periodes van de HSFL zijn significant kleiner dan de bestralingsgolflengte λ₀. Bijvoorbeeld, voor aluminium werd deze periode geschat op 20 tot 200 nm bij λ₀=0,8 µm. Terwijl de oriëntatie van de rimpels in gewone LIPSS loodrecht was op de laserlichtpolarisatie, was de oriëntatie van HSFL vaak loodrecht en soms parallel aan de polarisatie. Vergelijkbare HSFL werden gevormd op de oppervlakken van transparante diëlektrika, halfgeleiders en metalen. De oorsprong van HSFL werd verklaard door verschillende mechanismen zoals tweede-harmonische-generatie, betrokkenheid van specifieke typen plasmon-moden, zelforganisatie en lokale veldversterking tijdens inhomogene doorbraak in diëlektrische materialen.

Het doel van deze studie is om een golfproces te zoeken dat een patroon met een korte periode Λ≪λ₀ kan produceren. We onderzoeken eigenschappen van longitudinale (L) elektromagnetische golven in metalen, ook wel plasma-golven genoemd. Onze studie bestaat uit de volgende nieuwe stappen. Ten eerste begonnen we ons onderzoek met de definitie van de ruimtelijke dispersie van de permittiviteit. Zoals hieronder getoond, is de gangbare definitie nutteloos als het bestudeerde medium niet uniform en oneindig is. Daarom stellen we een nieuw concept van de ruimtelijk-dispersieve diëlektrische functie ε voor. Deze functie stelt de directe proportionaliteit vast tussen twee vectoraalvelden, E(r,ω) en D(r,ω), maar niet de amplitudes E(k,ω) en D(k,ω) van vlakke golven. Gevolgelijk hangt de hoeveelheid ε af van het kwadraat van het golgetal, k², de parameter van de vector-Helmholtz-vergelijking voor het elektrisch veld E(r,ω), maar niet de golfvector k van de vlakke golven. Vervolgens, om zo'n nieuwe functie af te leiden, bepaalden we de respons van de geleidingselektronen op een elektromagnetische modus door de Boltzmann-transportvergelijking op te lossen in de relaxatietijd-benadering. De zogenoemde transversale en longitudinale Lindhard-diëlektrische functies werden verkregen. Verder vonden we dat de longitudinale Lindhard en de veel eenvoudigere hydrodynamische functie in een brede parameterbereik dicht bij elkaar liggen. Licht-extinctie door zilver en goud nanospheres werd overwogen om de theorie te illustreren. We tonen voor het eerst aan dat de niet-lokale Mie-theorie de blauwverschuiving, verbreiding en eventuele verdwijning van de plasmon-resonanties verklaart die waargenomen worden met een afname van de grootte van edelmetaal-nanospheres. Tenslotte werd het nieuw ontwikkelde theoretische model toegepast om de mogelijkheid van betrokkenheid van de longitudinale modi in de vorming van laser-geïnduceerde oppervlaktestructuren te onderzoeken. Hiervoor wijzigden we de Fresnel-theorie rekening houdend met getransmitteerde longitudinale golven.

Methoden

Om de elektromagnetische velden in stuksgewijs homogene media te bepalen, werd de klassieke elektromagnetische theorie toegepast. Het elektrisch veld E in elk uniform domein van het heterogene medium werd verondersteld een oplossing te zijn van de vector-Helmholtz-vergelijking (VHE):

Δ E + k² E = 0, (1)

waar Δ de Laplace-operator is.

Zoals gebruikelijk, zijn de tangentiële componenten van het elektrisch E en magnetisch H veld continu over de grenzen van de media. Daarnaast namen we in aanmerking dat elektronen in het metaal zijn ingesloten; daarom werd de volgende additionele randvoorwaarde (ABC) voor de normale component van de stroomdichtheid j aan het metaaloppervlak S gebruikt: (j·n)|_r∈S = 0.

Om de geleidingsstroom in het metaal te bepalen, losten we de Boltzmann-transportvergelijking (BTE) op in de relaxatietijd-benadering:

∂f/∂t + v·∂f/∂r + (e/m)(E + v×B)·∂f/∂v = (f₀ - f)/τ, (2)

waar f de enkel-deeltjesverdelingsfunctie is in de faseruimte (r, v), v de microscopische elektronsnelheid, e en m de elektronlading en -massa, B de magnetische inductie, f₀ een evenwichtsverdelingsfunctie en τ de relaxatietijd.

Hieronder leiden we formules af voor de ruimtelijk-dispersieve diëlektrische functies. Vervolgens gebruiken we ze om lichtreflectie van een vlak metaaloppervlak en verstrooiing van licht op een edelmetaal-nanosphere te bestuderen.

Resultaten en discussie

Ruimtelijke dispersie van ε in een heterogeen medium

In de literatuur wordt een ruimtelijk-dispersieve diëlektrische functie ε gedefinieerd via de volgende relatie:

D(ω, r) = ε₀ ∫∫∫ ε(ω, r−r′) E(ω, r′) dr′, (3)

waar ε₀ de elektrische constante is, D(ω, r) de amplitude van de verplaatsingsvector-trilling met hoekfrequentie ω in punt r, en E(ω, r′) de amplitude van het elektrisch-veldtrilling in punt r′. Fourier-transformaties van Verg. (3) geven de vergelijking

D(ω, k) = ε₀ ε(ω, k) E(ω, k), (4)

waar een ruimtelijk-dispersieve ε(ω, k) afhangt van de golfvector k van een vlakke elektromagnetische golf. Ons inziens is Verg. (3) niet eenduidig alleen in een oneindig homogeen volume, maar we hebben te maken met een stuksgewijs heterogeen systeem waar grenzen in aanmerking genomen moeten worden en k niet hetzelfde is in verschillende media.

Onze benadering gebruikt geen uitbreiding van elektromagnetische golven over vlakke golven. De ruimtelijk-dispersieve permittiviteit bepaalt de relatie tussen D(ω, r) en een bijzondere oplossing van de vector-Helmholtz-Verg. (1):

D(ω, r) = ε₀ ε(ω, k) E(ω, r). (5)

Hier geeft E(ω, r) de verdeling van het elektrisch veld weer, niet slechts de vector E in punt r.

Longitudinale en transversale diëlektrische functies

De permittiviteit van metalen wordt doorgaans uitgedrukt door de geleidingscapaciteit σ:

ε = ε_g + iσ/(ωε₀), (6)

waar ε_g een deel van de diëlektrische functie is dat rekening houdt met polarisatie van het vaste stof; ε_g = 1 voor een eenvoudig metaal. Om σ te bepalen, berekenen we de stroomdichtheid

j = e ∫∫∫ v f dv = σ E, (7)

waar dv = (v/m) dε dΩ, dΩ = sinθ dθ dφ, v, θ, φ de spherische coördinaten van de snelheid zijn. In tegenstelling tot eerdere onderzoeken, introduceerden we niet de golfvector k, maar vonden een BTE-oplossing in de vorm van een oneindige reeks die operatoren v·∇ bevat die op v·E werken:

f = f₀ + (e/(-iω+Γ)) (∂f₀/∂ε) [1 + (v·∇)/(-iω+Γ)]⁻¹ v·E, (8)

waar Γ = 1/τ. Vervolgens werd f₀ benaderd door een nul-temperatuur Fermi-Dirac-verdeling en, na integratie over ε in Verg. (7), kregen we

j = (ω_p² ε₀/(-iω+Γ)) (3/4π) ∫∫ u (1 + l u·∇)⁻¹ (u·E) dΩ, (9)

waar ω_p² = e² n_e/(m ε₀), ω_p de plasmafrequentie is, u = v/v de eenheidsvector in de richting van v, l = v_F/(-iω+Γ), v_F de Fermisnelheid. Vervolgens berekenen we de integralen

∫∫ u (u·E) dΩ = (4π/3) E, (10)

∫∫ u (u·∇)^2n-1 (u·E) dΩ = 0, (11)

∫∫ u (u·∇)²ⁿ (u·E) dΩ = (4π/(2n+3)) Δ^n-1 [∇(∇·E) - 1/(2n+1) ∇×∇×E], (12)

waar n een natuurlijk getal is. De volgende afhankelijkheid van j van een willekeurig elektrisch veld E werd verkregen:

j = (ω_p² ε₀/(-iω+Γ)) {E + 3 Σ_n=1^∞ l²ⁿ (Δ^n-1/(2n+3)) [∇(∇·E) - (∇×∇×E)/(2n+1)]}. (13)

Er zijn twee typen oplossingen voor Verg. (1), divergentievrije die ∇·E = 0 voldoen en rotatievrije die voldoen aan

∇ × E = 0. (14)

Voor een vlakke golf, met E ∝ exp[i(k·r - ωt)], transformeert Verg. (14) in de relatie k×E = 0, wat aantoont dat de golf longitudinaal (L) is. Om processen in spherische lichamen te simuleren, is het handig om de vector-sferische harmonischen L, M en N als een complete set orthogonale functies te gebruiken. In dit geval specificeert Verg. (14) harmonischen L. Het golgetal van de L-golven en L-modi wordt bepaald door de volgende dispersiewet:

ε^L(ω, k^L) = 0. (15)

Uit Verg. (6) en (13) vinden we dat oplossingen van Verg. (1) die de beperking van Verg. (14) voldoen, de volgende longitudinale permittiviteit geven:

ε^L = ε_g - (ω_p²/(ω(ω+iΓ))) (3/2) Φ(a², 1, 3/2), (16)

waar Φ de Lerch's Phi-functie is,

(3/2) Φ(a², 1, 3/2) = Σ_n=0^∞ (3/(2n+3)) a²ⁿ, (17)

a = k v_F/(ω + iΓ).

De verkregen permittiviteit verschilt van die gedefinieerd door Kliewer en Fuchs slechts in notatie:

ε^L = ε_g + (ω_p²/(ω(ω+iΓ))) (3/a²)[1 - (1/(ia)) tan^-1(ia)], (18)

De identiteit (1/(ia)) tan^-1(ia) = (1/2) ln((1+a)/(1-a)) (19) stelt ons in staat om Verg. (18) als volgt herschrijven:

ε^L = ε_g - (ω_p²/(ω(ω+iΓ))) (3/a²)[1 - (1/(2a)) ln(1+a)/ln(1-a)]. (20)

In het geval Γ = 0 neemt deze formule de vorm aan van een vergelijking afgeleid door Klimontovich en Silin, die Landau-demping in gedegeneerd plasma bestudeerden. De permittiviteit van de equivalente Verg. (16), (18) en (20) wordt algemeen de Lindhard-diëlektrische functie genoemd (met verwijzing naar [12]), hoewel deze functie eerst verkregen werd door Klimontovich en Silin.

De transversale Lindhard-permittiviteit kan gevonden worden met Verg. (13) wanneer ∇·E = 0. In het werkelijke geval van v_F k ≪ ω, vereenvoudigt het tot de Drude-diëlektrische functie:

ε^T = ε_g - ω_p²/(ω² + iΓω). (21)

Deze functie stemt overeen met experimentele data op veel metalen. Als |a| < 1, vereenvoudigt de longitudinale permittiviteit (16) tot de hydrodynamische diëlektrische functie:

ε^L(ω, k^L) = ε_g - ω_p²/(ω² + iΓω - (3/5)(v_F k^L)²). (22)

Reflectie van een vlakke elektromagnetische golf van een plat metaaloppervlak

Randvoorwaarden

In deze sectie bepalen we de richting van de golfvector k^L en de amplitude van de L-golf geëxciteerd in het metaal tijdens reflectie van een vlakke elektromagnetische golf van een plat metaaloppervlak.

Overweeg een vlakke golf incident op de diëlektrik-metaal-interface z=0 met de golfvector in het xz-vlak. Het elektrisch veld in diëlektrisch medium 1 bestaat uit de incidente E_i en gereflecteerde E_r golven, het veld in metaal 2 heeft de getransmitteerde transversale E_t en, in sommige gevallen, longitudinale E^L componenten. Volgens de Maxwell-randvoorwaarden zijn de transversale componenten van de elektrische en magnetische veldvectoren continu in het vlak z=0. Daarnaast worden elektronen niet uit het metaal geëjecteerd; daarom is de normale component van de elektrische stroomdichtheid nul bij z=0:

ẑ·j|_{z=0} = 0, (23)

waar ẑ de eenheidsvector in de z-richting is.

Alle termen in de Maxwell-randvoorwaarden moeten dezelfde afhankelijkheid van x en y hebben. Deze vereiste heeft diverse gevolgen. Ten eerste kan vastgesteld worden dat L-golven alleen geëxciteerd kunnen worden in het geval van p-polarisatie wanneer de elektrische vector van de incidente golf E⁽ⁱ⁾ parallel is aan het incidentievlak. Met andere woorden, plasmon-polaritonen kunnen gegenereerd worden door een transversaal-magnetische (TM) golf. Het effect is vergelijkbaar met dat in een metaalsfeer. Ten tweede kunnen formules analog aan de wet van Snell afgeleid worden uit de voorwaarden:

k_1x = k_2x = k_2x^L = k₁ sinθ₁, (24)

waar indexen 1x en 2x de x-projecties van de vectoren in media 1 en 2 aanduiden, θ₁ de incidentiehoek is.

Reflectie- en transmissiecoëfficiënten

Laten ons het veld bepalen gevormd door een p-gepolariseerde vlakke elektromagnetische golf incident op een plat metaaloppervlak. Het is handig om de componenten van de elektrische en magnetische velden uit te drukken door de x-component van E⁽ⁱ⁾, namelijk E_x(r) = -r E_x(i) voor de gereflecteerde golf, E_x(t) = t E_x(i) voor de getransmitteerde transversale golf, en

E_x^(a) = δ E_x^(t) = t_L E_x⁽ⁱ⁾, (25)

voor de getransmitteerde longitudinale golf, waar r een reflectiecoëfficiënt is, t en t_L transmissiecoëfficiënten. Uit de Maxwell-randvoorwaarden en ABC van Verg. (23) geschreven in de vorm

ẑ·(D - ε₀ε_g E)|_{z=0} = 0, (26)

kregen we

r = -((1+δ)ε₁k_2z - ε₂k_1z)/((1+δ)ε₁k_2z + ε₂k_1z) = 1 - (1+δ)t, (27)

t = 2ε₁k_2z/(ε₂k_1z + (1+δ)ε₁k_2z), (28)

δ = (ε_g - ε)/ε_g (k_2x²/(k_2z k_2z^L)), (29)

Bij δ = 0 wordt de coëfficiënt r de Fresnel-reflectiecoëfficiënt van de p-gepolariseerde golf. Onder dezelfde voorwaarde is t niet de Fresnel-transmissiecoëfficiënt, aangezien onze definities van t en r verschillen van die van Fresnel.

Extinctie van licht door metaal-nanosphere

In een voorgaand artikel generaliseerde een van de auteurs de Lorentz-Mie-theorie rekening houdend met de ABC van Verg. (23). Een analogon van de Fresnel-coëfficiënt r, de Mie-coëfficiënt b_l voor de gereflecteerde TM-modus van de l-de orde, werd gevonden als:

b_l = -((1+δ_l)ε₁ (k₂ ψ'_l(k₂R)/ψ_l(k₂R)) - ε₂ (k₁ ψ'_l(k₁R)/ψ_l(k₁R))) / ((1+δ_l)ε₁ (k₂ ψ'_l(k₂R)/ψ_l(k₂R)) - ε₂ (k₁ ζ'_l(k₁R)/ζ_l(k₁R))), (30)

waar

δ_l = (ε^T - ε_g)/ε_g (l(l+1) j_l(k₂R) j_l(k₂^LR) / (ψ'_l(k₂R) k₂^LR j'_l(k₂^LR))), (31)

ψ_l en ζ_l zijn de Riccati-Bessel en Riccati-Hankel functies van de l-de orde, respectievelijk; j_l is de sferische Bessel-functie, de prime duidt de afgeleide van een functie ten opzichte van zijn argument aan.

Laten we voorspellingen van de klassieke en gegeneraliseerde Lorentz-Mie-theorieën vergelijken met experimentele data. In [15] bestudeerden Hilger, Tenfelde en Kreibig extinctiespectra van zilvernanodeeltjes gedeponeerd op diëlektrische oppervlakken. In de eerste fase van de studie genereerden de onderzoekers bundels zilverdeeltjes met gemiddelde diameters van 2, 3,5 en 4 nm, bepaalden de deeltjesgrootteverdeling voor een van de bundels, noteerden extinctiespectra en schatten parameter A=0,25 van de fenomenologische formule Γ = Γ_b + A v_F/R, waar Γ_b de bulk-metaal-relaxatiesnelheid is, voor zilversferen in vacuüm. Eerst berekenen we de extinctiespectra voor een bundel zilversferen met gemiddelde diameter 〈D〉=2 nm en experimentele grootteverdeling die het gebied van D=1 tot D=4 nm beslaat. Onze theorie bevat geen aanpasbare parameters. Om de diëlektrische functies te definiëren, gebruikten we de tabulatie van de brekingsindex van bulkzilver voorgesteld door Lynch en Hunter [16] (zie Fig. 1). We pasten ook Verg. (16), (21) en (22) toe met ω_p=9,17 eV, Γ_b=0,021 eV, v_F=1,39×10⁶ m/s en A=0,25. De berekeningsresultaten en experimentele spectrum worden gepresenteerd in Fig. 2.

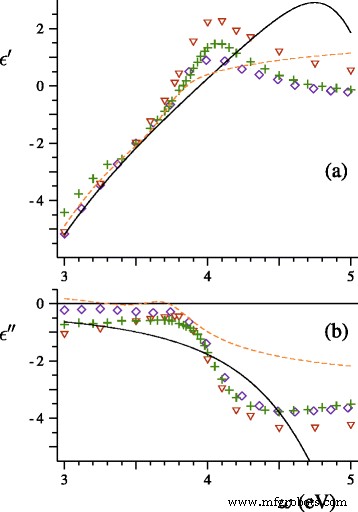
Reële (a) en imaginaire (b) delen van de diëlektrische functie van zilver volgens Johnson en Christy (◇) [20], Lynch en Hunter (+) [16], Weber (△) [21], Hao en Nordlander (gestippelde lijn) [22], en Drachev et al. (doorgetrokken lijn) [23]

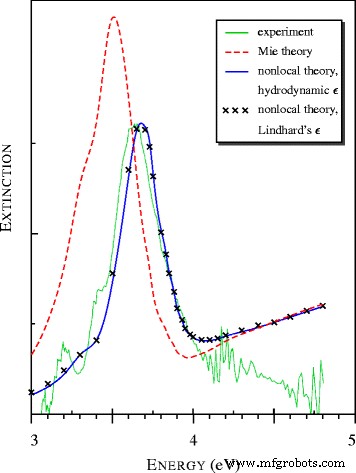
Spectra van licht-extinctie door zilver nanometer-grote deeltjes waargenomen in [15] en berekend met lokale en niet-lokale modellen. Alle theoretische spectra worden gepresenteerd in gemeenschappelijke relatieve eenheden.

De theoretische spectra in Fig. 2 werden berekend met de Klimontovich-Silin-Lindhard en de veel eenvoudigere hydrodynamische diëlektrische functies. Het is verrassend dat beide berekeningen nauwkeurige resultaten gaven, zelfs hoewel |a| > 1 in het gebied van de plasmon-resonantie.

Voor de nanometer-grote zilversferen verschuift het maximum in het extinctiespectrum, de Fröhlich-, plasmon- en oppervlakte-plasmon-polariton-resonantie (SPP), van 3,5 tot 3,65 eV. Het niet-lokale model is in uitstekende overeenstemming met de experimentele data, terwijl de lokale (Mie)-theorie het maximum geeft bij ω≃3,5 eV (zie Fig. 2 en Tabel 1).

De berekening van de blauwverschuiving van de plasmon-resonantie kan ondersteund worden door de volgende overweging. In de elektrostatische benadering draagt alleen b₁ bij aan het extinctiekruissnede Q_ext en Verg. (30) kan vereenvoudigd worden door de volgende benaderingen te gebruiken:

k₂R ψ'_l(k₂R)/ψ_l(k₂R) ≃ l+1; k₁R ζ'_l(k₁R)/ζ_l(k₁R) ≃ -l. (32)

Dus, Q_ext heeft een maximum bij

Re[2(1+δ₁)ε₁ + ε₂] = 0. (33)

De verkregen voorwaarde (33) rekening houdend met excitatie van de L-modi (door de term δ₁) en verschilt daarom van de Fröhlich-resonantievoorwaarde: Re(2ε₁ + ε₂) = 0. (34)

In experiment [15] waren de piekfrequenties ω_m en resonantiebreedtes Δω van de extinctiespectra bijna onafhankelijk van 〈D〉. Dit kenmerk van Δω lijkt in tegenspraak te zijn met de klassieke Mie-theorie. Werkelijk, de lokale theorie voorspelt verbreiding van de plasmon-resonanties met afname van D (bij A=0,25) zoals getoond in Tabel 1. Tegelijkertijd geeft de niet-lokale theorie ongeveer gelijke resonantiebreedtes maar verschillende piekposities. Superpositie van de bijdragen van alle deeltjes geeft de waarde van Δω die in opmerkelijke overeenstemming is met de experimentele data. Het is interessant dat de niet-lokale theorie een verbreiding van de plasmon-resonantie van een bundel voorspelt zelfs bij A=0.

Bij ω > 4 eV liggen de gladde theoretische krommen in Fig. 2 hoger dan de mengeling van nauwgelegen experimentele pieken. De interband-absorptie domineert in dit spectrale bereik, wat bevestigd kan worden door Fig. 1. De waargenomen eigenaardigheden van het spectrum zijn waarschijnlijk een gevolg van een overgang van de continue banden naar een discrete niveaustructuur. Zo'n kwantum-grootte-effect werd eerder ontdekt in een studie van de optische eigenschappen van goud-nanospheres. Toen de zilversfeer-grootte werd verhoogd tot 〈D〉=3,5 nm, nam de absorptie eerst toe ten opzichte van het maximum en vormde een plateau met een reeks kleine gelijkmatige dips. Vervolgens nam de absorptie licht af bij 〈D〉=4 nm.

Om de vorming van de blauwe vleugel van de plasmon-resonantie te bestuderen, berekenen we de extinctiespectra van ultra-kleine zilverdeeltjes en presenteren ze in Fig. 3. Een opmerkelijk kenmerk in Fig. 3 is het complete verdwijnen van de plasmon-resonantie bij D=1 nm. Vroeger werd dit effect waargenomen in de experimentele studie van goud-nanospheres. In het bijzonder, in Fig. 9 van [19], werden de experimentele spectra van deeltjes met diameters van 1,7, 1,9, 2,0, 2,1, 2,3 en 2,5 nanometer vergeleken met de spectra berekend met de lokale Mie-theorie. De overeenstemming was slecht, niet in staat om de verbreiding van de plasmon-resonantie en zijn positie te beschrijven. Pogingen om de fit te verbeteren door de deeltjesgrootte te variëren en modificaties van de diëlektrische functies waren niet succesvol. Volgens de auteurs van [19] weerstoot de waargenomen abnormaal brede of gedempte collectieve oscillatieband de voorgestelde correcties van de lokale Mie-theorie. Zoals te zien is in Fig. 4, verandert de situatie dramatisch als de niet-lokale Mie-theorie wordt toegepast. Let op dat we geen aanpasbare parameters gebruikten. De tabulatie van de complexe brekingsindex door Johnson en Christy [20] werd gebruikt om de diëlektrische functie van goud te bepalen. Andere parameters, inclusief A=1 en brekingsindex van tolueen (1,37) werden overgenomen uit [19].

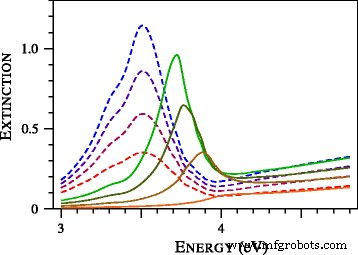
Genormaliseerde extinctiekruissnede van zilverdeeltjes met diameters van 2,2, 1,8, 1,4 en 1,0 nm berekend met lokale (gestippelde lijnen) en niet-lokale (doorgetrokken krommen) Mie-theorieën. Hoe kleiner het deeltje, hoe lager de kromme. Alle theoretische kruissnedes worden gepresenteerd in gemeenschappelijke relatieve eenheden.

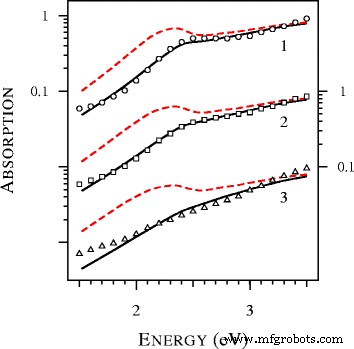
Absorptiespectra berekend met de lokale (gestippelde lijnen) en niet-lokale (doorgetrokken lijnen) Mie-theorie en experimentele data (stippels) geëxtraheerd uit Fig. 9 van [19] voor goudsferen met D=2,5, 2,1 en 1,7 nm in tolueen (krommen 1 en cirkels, krommen 2 en vierkanten, en krommen 3 en driehoeken, respectievelijk). Alle theoretische spectra genormaliseerd tot eenheid bij 4,12 eV en verticaal verschoven.

Golgetallen van de longitudinale golven

De longitudinale modi verschillen van de transversale door veel hogere waarden van de golgetallen. Bijvoorbeeld, voor de berekeningen gepresenteerd in Fig. 2, correspondeert het reële deel van k₂^L met de ruimtelijke periode Λ = 2π/Re k₂^L dalend van 9 tot 2 nm bij ω stijgend van 3 tot 4 eV. In dit ω-interval daalde de absolute waarde van de verhouding k₂^L/k₂ van 130 tot 100 en de parameter δ van Verg. (27) daalde van 0,01 tot 0,005 bij θ₁=π/4. We concluderen daarom dat excitatie van de L-golven bij een vlak ziloppervlak verwaarloosbaar is. Echter, de L-modi zijn van belang gebleken in nanometer-grote zilverclusters.

Een vervanging van de term -ω_p²/(ω²+iΓω) in Verg. (16) door ε^T−ε_g volgens Verg. (21) stelt ons in staat om de dispersievergelijking (15) als volgt te herschrijven:

1 + (3/5)a² + (3/7)a⁴ + (3/9)a⁶ + ... = 1/(1 - ε^T/ε_g). (35)

In het eenvoudigste geval van ε_g = 1 en Γ = 0 voorspelt Verg. (35) dat metaal transparant is voor zowel transversale als L-golven bij ω > ω_p, maar zowel k^L als k^T zijn complex bij ω < ω_p.

Als het vaste stof transparant is, kan een longitudinale golf geëxciteerd worden onder schuine incidentie van een p-gepolariseerde golf op een vlak oppervlak. Er zijn diverse kenmerkende aspecten van dit effect. Ten eerste kunnen longitudinale golven gegenereerd worden aan een vlak oppervlak, terwijl speciale inspanningen nodig zijn om oppervlakte-plasmon-polaritonen te exciteren. Ten tweede is in het interferentiepatroon de elektromagnetische-veldensiteit gemoduleerd niet langs maar loodrecht op de interface. Daarom kunnen gaten verschijnen in vlakken parallel aan het oppervlak door spallatie van het vaste stof. Volgens de definitie van ω_p kan de voorwaarde ω > ω_p voldaan worden in vaste stoffen (bijvoorbeeld halfgeleiders) met een lage dichtheid van ladingdragers. We onderzoeken dit geval niet hier omdat de formule van ε^L is afgeleid voor gedegeneerd elektrongas.

Conclusies

Om een ruimtelijk-afhankelijke diëlektrische functie te definiëren, keken alle eerdere onderzoekers naar de interactie van materie met een vlakke elektromagnetische golf. Deze benadering is niet constructief en rigoreus in nano-optica wanneer het veld gelokaliseerd is in een caviteit en de randvoorwaarden op een of andere manier in aanmerking genomen moeten worden. We hebben dit probleem opgelost door de respons van het medium op een elektrisch veld te berekenen dat de vector-Helmholtz-vergelijking voldoet. De afgeleide ruimtelijk-dispersieve diëlektrische functie hangt af van het kwadraat van het golgetal, een parameter van de Helmholtz-vergelijking, maar niet de golfvector van een vlakke golf.

We rapporteren de Fresnel-reflectiecoëfficiënten gewijzigd door excitatie van longitudinale golven in metalen. Een vergelijkbare generalisatie werd eerder gemaakt voor de Mie-coëfficiënten. Hierin is de theorie geverifieerd met simulatie van licht-extinctie door nanometer-grote zilver- en goudclusters. De berekende verschuiving van 3,5 tot 3,65 eV en de breedte van de oppervlakte-plasmon-resonantie van de zilverdeeltjes-bundel zijn in uitstekende overeenstemming met de experimentele data. Daarnaast verklaart het niet-lokale model het verdwijnen van de plasmon-resonantie van gouden spheren met diameters van ongeveer 2 nm. Het is belangrijk dat L-golven kunnen worden geëxciteerd op een vlak oppervlak door een vlakke incidente golf. Dit is het belangrijkste verschil van de plasmon-polaritonen van de oppervlakte-plasmon-polaritonen.

De eigenschappen van de elektromagnetische oscillaties in metalen zijn onderzocht. Het is gevonden dat de absolute waarden van de golgetallen van de longitudinale golven veel groter zijn dan die van de transversale golven. Bijvoorbeeld, in zilver bij een fotonenergie van 3,5 eV is de verhouding van de absolute waarden van de golgetallen gelijk aan 130. Daar correspondeert het reële deel van het golgetal van de longitudinale golf met een golflengte van 7 nm. Het grote verschil in golgetallen voorkomt excitatie van de L-golven aan een planaire interface. Echter, de L-modi zijn aangetoond geëxciteerd in zilver- en goud-nanometer-grote deeltjes.