Spin-onafhankelijke plasmonische lens

Abstract

Voor de halfronde plasmonische lens is de spiraalfase de oorsprong van de spin-afhankelijke oppervlakteplasmonpolariton (SPP) focussering. Door de spinafhankelijke spiraalfase te compenseren met een andere spiraalfase of Pancharatnam-Berry-fase, realiseerden we de SPP-focussering onafhankelijk van de spintoestanden van het excitatielicht. Analyses gebaseerd op zowel het Huygens-Fresnel-principe voor SPP's als numerieke simulaties bewijzen dat de positie, intensiteit en het profiel van de SPP-focussen precies hetzelfde zijn voor verschillende spintoestanden. Bovendien is de spin-onafhankelijke SPP-focussering immuun voor de verandering van de straal, de centrale hoek en de vorm van de halfronde spleet. Deze studie onthult niet alleen het mechanisme van spinafhankelijke SPP-apparaten, maar biedt ook effectieve benaderingen om de invloed van spintoestanden op het SPP-veld te overwinnen.

Inleiding

In de driedimensionale (3D) vrije ruimte spelen optische lenzen een onmisbare rol bij het vormen van de lichtstroom, zoals focussering, beeldvorming en optische Fourier-transformatie (FT). De inherente beperkingen van conventionele lenzen worden echter ook geleidelijk onthuld. Door de diffractie van licht is de transversale volledige breedte op half maximum van een focus maar liefst ongeveer een halve golflengte λ /(2n sin α ), wat de realisatie van superresolutielithografie en microscopie belemmert [1,2,3]. Wat betreft de optische FT-relatie tussen de voorste en achterste brandpuntsvlakken, wordt de snelheid van de transformatie beperkt door de dikte en brandpuntsafstand van de lens [4]. Vooral, vergeleken met de golflengte van licht, is het volume van de lens omvangrijk vanwege het gebogen oppervlak dat wordt gebruikt om geleidelijke fase-accumulatie te bereiken [5,6,7]. En dat is onverenigbaar met de toenemende vraag naar miniatuur en geïntegreerde optische apparaten in onderzoek en toepassingen [8,9,10].

Surface plasmon polaritons (SPP's), hybride modi van fononen en elektronische oscillaties die zich voortplanten langs de tweedimensionale (2D) metaal/diëlektrische interface, kunnen een effectief hulpmiddel zijn om de bovenstaande beperkingen te overwinnen [11,12,13,14,15,16, 17]. Met de subgolflengte-functie kunnen SPP's eenvoudig worden scherpgesteld op een subgolflengte-spot [18,19,20,21]. Als de tegenhanger van de optische lens in de 3D-ruimte, kan de halfronde spleetplasmonische lens niet alleen SPP-velden focusseren, maar ook SPP FT met een veel hogere snelheid uitvoeren in een 2D-vlak [4]. Bovendien, om SPP's effectief te exciteren, is de breedte van de spleet kleiner dan de golflengte van invallend licht. Desalniettemin hangt de focussering van SPP's gegenereerd door de halfronde spleet sterk af van de spintoestanden van het invallende licht [22,23,24,25]. Voor links circulair gepolariseerd (LCP) en rechts circulair gepolariseerd (RCP) invallend licht, zullen de brandpunten van SPP's spinafhankelijke transversale verschuivingen ervaren, wat zich onderscheidt van de focussering van circulair gepolariseerd licht in de vrije ruimte. Sinds de studie van de spin-afhankelijke halfronde SPP-lens in 2008 door Hasman et al. [22,23,24], er zijn verschillende mechanismen voorgesteld om de spinafhankelijke SPP-focussering te bewerkstelligen [26,27,28]. Het basisprincipe is gebaseerd op de spinafhankelijke faseverdeling die wordt bereikt door de oriëntatiehoeken van subgolflengtespleten te sturen. Bovendien zijn spin-afhankelijke SPP-excitatie [29], SPP-vortex [30], SPP-hologram [31], SPP Bessel-straal [32] en SPP Airy-straal [33] aangetoond. Over het algemeen zijn spin-afhankelijke SPP-apparaten uitgebreid bestudeerd. Het is duidelijk en normaal dat de spintoestanden van excitatielicht de functionaliteit van SPP-apparaten kunnen beïnvloeden, omdat zelfs de SPP's die worden geëxciteerd door een enkele spleet of gat met een subgolflengte afhankelijk zijn van de spintoestanden [24, 26, 28, 33]. Is het daarentegen mogelijk om de invloed van spintoestanden op het SPP-veld te vermijden en de SPP-lens spinonafhankelijk te maken?

De SPP's gegenereerd door een halfronde spleet zijn bedrukt met een spinafhankelijke spiraalfase exp(iσ _± θ ), waarbij de spin aangeeft σ _± = ± 1 vertegenwoordigt respectievelijk LCP- en RCP-licht [22,23,24,25]. In dit artikel stellen we een globale en een lokale benadering voor om de invloed van de spiraalfase te elimineren en spin-onafhankelijke SPP-focus te bereiken. De globale benadering behandelt de halfronde spleet volledig en heft de spiraalfase op door een tegenoverliggende halfronde spleet toe te voegen die een omgekeerde spiraalfase kan introduceren. Wat betreft de halfronde spleet als de samenstelling van subgolflengtespleten, kan de spiraalfase lokaal worden gecompenseerd met Pancharatnam-Berry-fase die wordt afgestemd door de oriëntatiehoek van de spleet te veranderen. De spin-onafhankelijke SPP-focussering wordt geanalyseerd en geverifieerd met het Huygens-Fresnel-principe voor SPP's en numerieke simulaties. De robuustheid van de voorgestelde benaderingen wordt getest door de straal, de centrale hoek en de vorm van de halfronde spleet te veranderen. Vergeleken met eerdere spin-afhankelijke SPP-apparaten [26,27,28,29,30,31,32,33], is de focussering van SPP's hier onafhankelijk van de spintoestanden van het excitatielicht, wat de stabiliteit van de SPP zou kunnen verbeteren lens.

Resultaten en discussies

Spin-onafhankelijke plasmonische lens bestaande uit dubbele halfronde sleuven

Voor halfronde spleetplasmonische lens verlicht door links circulair gepolariseerd (LCP) en rechts circulair gepolariseerd (RCP) invallend licht, nemen de spiraalfasen toe van 0 tot π respectievelijk tegen de klok in en met de klok mee, zoals schematisch weergegeven in Fig. 1b. De spiraalvormige fase is het resultaat van de interactie tussen het circulair gepolariseerde licht en de anisotrope structuur op nanoschaal [23]. Circulair gepolariseerd licht is de synthese van horizontaal gepolariseerd en verticaal gepolariseerd licht met een π /2 faseverschil. De SPP's die worden opgewekt door de twee lineaire componenten kunnen worden uitgedrukt als sinθ en cosθ , respectievelijk [25]. Het SPP-veld dat wordt gegenereerd door circulair gepolariseerd licht is dus sinθ + exp(iσ _± π /2) cos θ = exp(iσ _± θ ). Zonder de spiraalfase zou het golffront van SPP's evenwijdig zijn aan de halfronde spleet en de SPP-golfvector k _sp langs de radiale richting zou zijn. De spiraalfase komt echter overeen met een spiraalvormig golffront en de SPP-golfvector zal afwijken van de radiale richting, geïllustreerd door de rode en blauwe pijlen in figuur 1a. En uiteindelijk resulteert de spiraalfase in de transversale verschuiving van de SPP-focus [22, 23, 25]. Het is duidelijk dat de spin-afhankelijke spiraalfase, die de oorsprong is van de spin-gecontroleerde SPP-focussering, moet worden geëlimineerd om de spin-onafhankelijke SPP-lens te realiseren.

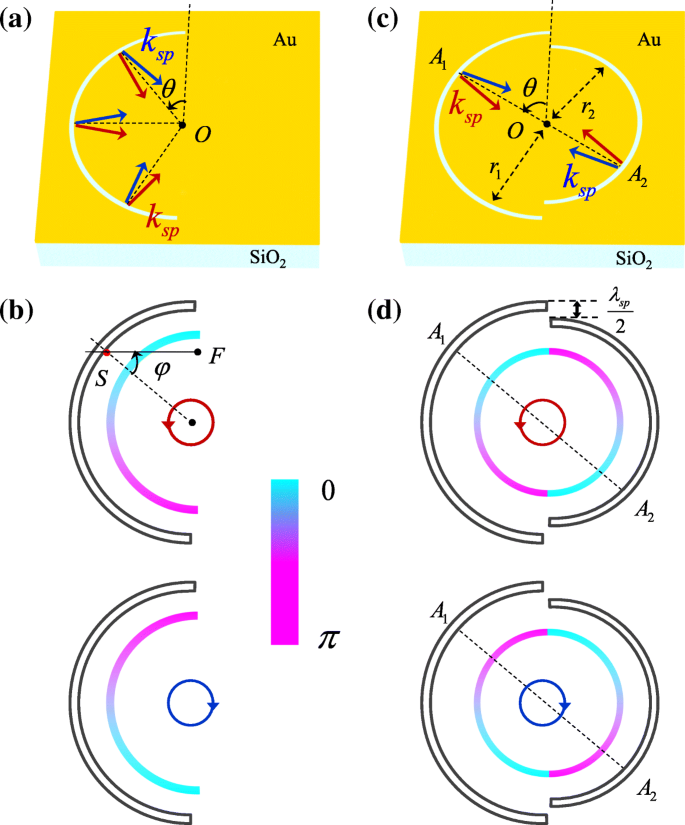
Schematisch diagram van de halfronde spleetplasmonische lens (a ) en de spin-onafhankelijke SPP-lens bestond uit twee halfronde sleuven (c ). Met de verlichting van LCP- en RCP-licht zullen de aangeslagen SPP's spinafhankelijke spiraalfasen ervaren (b ). Het toevoegen van nog een halfronde spleet kan een extra spiraalvormige fase introduceren, en de twee spiraalvormige fasen kunnen elkaar opheffen wanneer r ₁ − r ₂ = λ _sp /2 (d )

Het toevoegen van nog een halfronde spleet om extra spiraalvormige fase te introduceren zou een oplossing kunnen zijn. Wanneer de twee halfronde sleuven zich aan dezelfde kant bevinden, kunnen de twee spiraalvormige fasen elkaar niet opheffen. De halfronde spleet moet dus aan de andere kant worden toegevoegd. Figuur 1c toont schematisch de structuur van de SPP-lens die bestond uit twee halfronde sleuven met verschillende straal r ₁ en r ₂ . De aangeslagen SPP-velden langs de linker en rechter halfronde spleten kunnen dienovereenkomstig worden uitgedrukt als:

$$ {E}_{\mathrm{sp}}^{\mathrm{L}}\left({r}_1,\theta \right)=\exp \left(i{\sigma}_{\pm} \theta \right),\left(0\le \theta \le \pi \right), $$ (1) $$ {E}_{\mathrm{sp}}^{\mathrm{R}}\left ({r}_2,\theta \right)=\exp \left(i{\sigma}_{\pm}\theta \right),\left(\pi \le \theta \le 2\pi \right) . $$ (2)

Er bestaat een π faseverschil tussen de spiraalvormige fasen gegenereerd door twee halfronde spleten. Vooral wanneer de stralen voldoen aan Δr = r ₁ − r ₂ = λ _sp /2, k _sp Δr = π zou gewoon de π . kunnen compenseren faseverschil tussen de twee spiraalfasen. Zoals weergegeven in figuur 1d, is de overeenkomstige fase van SPP's centrale symmetrie. Concreet, de fase van SPP's gegenereerd vanaf het punt A ₁ is hetzelfde als de fase van SPP's gegenereerd uit het symmetrische punt A ₂ . En de SPP's gegenereerd door A ₁ en A ₂ zal constructief interfereren in het midden, net als de andere punten langs de halfronde spleten. Dienovereenkomstig zullen de SPP's die worden gegenereerd door de twee halfronde spleten in het midden worden gefocusseerd zonder transversale verschuiving. Wanneer de spintoestanden van het invallende licht worden gewijzigd, zullen de linker- en rechterspiraalfasen gelijktijdig worden omgekeerd en blijven ze centrale symmetrie. Daarom kunnen de SPP's die door zowel LCP- als RCP-licht worden geëxciteerd, worden gefocusseerd in het midden van de halfronde, wat het spinonafhankelijke kenmerk van de plasmonische lens aangeeft.

De prestatie van de spin-onafhankelijke plasmonische lens wordt analytisch onderzocht met het Huygens-Fresnel-principe voor SPP's [34, 35]. In het poolcoördinatensysteem kunnen de SPP-velden die worden gegenereerd door de linker en rechter halfronde spleten respectievelijk worden uitgedrukt als:

$$ {E}_{\mathrm{sp}}^{\mathrm{L}}\left(\rho, \theta \right)=-\frac{i}{\sqrt{\lambda_{\mathrm{sp }}}}{\int}_0^{\pi}\cos \varphi {E}_{\mathrm{sp}}^{\mathrm{L}}\left({r}_1,\theta \right) \frac{\exp \left({ik}_{\mathrm{sp}}d\right)}{\sqrt{d}}\exp \left( i\pi /4\right){r}_1 d\ theta, $$ (3) $$ {E}_{\mathrm{sp}}^{\mathrm{R}}\left(\rho, \theta \right)=-\frac{i}{\sqrt{ \lambda_{\mathrm{sp}}}}{\int}_{\pi}^{2\pi}\cos \varphi {E}_{\mathrm{sp}}^{\mathrm{R}}\ left({r}_2,\theta \right)\frac{\exp \left({ik}_{\mathrm{sp}}d\right)}{\sqrt{d}}\exp \left( i\ pi /4\right){r}_2 d\theta . $$ (4)

waar φ geeft de hoek aan tussen de radiale richting en het voortplantingspad van de SPP en d is de afstand van de secundaire bron tot een willekeurig punt F , zoals weergegeven in Fig. 1b. Vervanging van Eq. (1) en vgl. (2) in Vgl. (3) en vgl. (4), de SPP-veldverdelingen kunnen worden verkregen en worden gegeven in Fig. 2a-d. De witte gestippelde halve cirkel vertegenwoordigt de halfronde spleet en de horizontale stippellijn is getekend om de transversale verschuiving van de focus van SPP's duidelijk weer te geven. Het is te zien dat de richting van de transversale verschuiving van de SPP-focus altijd tegengesteld is voor de linker en rechter halfronde spleten. Voor de spinonafhankelijke plasmonische lens is de SPP-verdeling de superpositie van de SPP-velden gegenereerd door twee halfronde spleten, die kan worden geschreven als $ {E}_{\mathrm{sp}}\left(\rho, \theta \right)={E}_{\mathrm{sp}}^{\mathrm{L}}\left(\rho, \theta \right)+{E}_{\mathrm{sp}}^{\mathrm {R}}\links(\rho, \theta \rechts) $. De intensiteit van SPP's in het centrum is dus

$$ {\displaystyle \begin{array}{c}{I}_{s\mathrm{p}}\left(0,\theta \right)={\left|{E}_{\mathrm{sp} }\left(0,\theta \right)\right|}^2={\left|{E}_{\mathrm{sp}}^{\mathrm{L}}\left(0,\theta \right )+{E}_{\mathrm{sp}}^{\mathrm{R}}\Big(0,\theta \Big)\right|}^2\\ {}={I}_{\mathrm{ sp}}^{\mathrm{L}}\left(0,\theta \right)+{I}_{\mathrm{sp}}^{\mathrm{R}}\left(0,\theta \right )+2\sqrt{I_{\mathrm{sp}}^{\mathrm{L}}\left(0,\theta \right){I}_{\mathrm{sp}}^{\mathrm{R} }\left(0,\theta \right)}\cos {\Delta \Phi}_{\mathrm{sp}},\end{array}} $$ (5)

waarbij het faseverschil ΔΦ_sp . is = k _sp (r ₁ − r ₂ ) − π en de term π het resultaat van het verschil tussen de linker en rechter spiraalfasen. Om spin-onafhankelijke focussering te realiseren, moeten de SPP's constructief interfereren in het centrum. De radiussen van de spleten moeten dus voldoen aan

$$ \Delta r=\left(2n+1\right)\frac{\lambda_{\mathrm{sp}}}{2},\left(n=\cdots -2,-1,0,1,2 ,\cdots \rechts). $$ (6)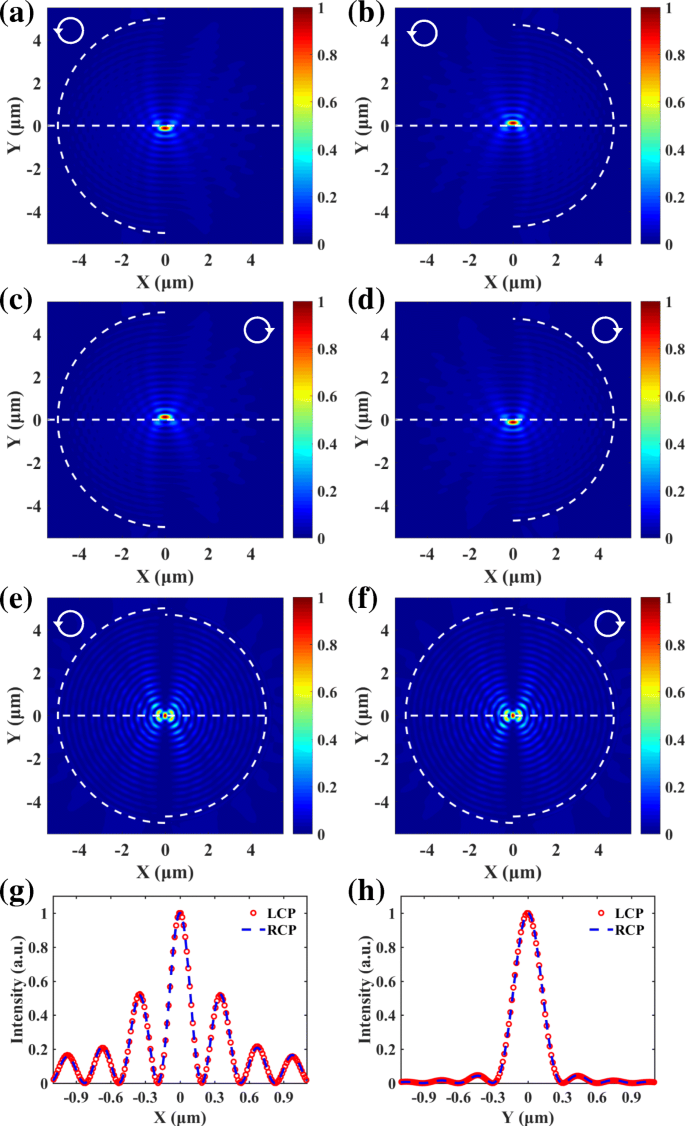

Voor LCP-licht wordt de SPP-focus gegenereerd door de linker halve cirkelspleet (a ) en de rechter halve cirkel spleet (b ) respectievelijk naar beneden en naar boven verschuiven. Voor RCP-licht c en d , zijn de posities van de SPP-focussen omgekeerd. e , v De SPP-focussen gegenereerd door spin-onafhankelijke plasmonische lens zijn allemaal in het midden voor LCP- en RCP-licht. g , u De transversale en longitudinale verdelingen van de SPP-focussen

Zoals weergegeven in Fig. 2e en f, zijn de SPP-velden die worden gegenereerd door LCP- en RCP-licht allemaal gefocust in het midden. De golflengte van invallend licht is 632,8 nm, en de corresponderende golflengte van de SPP's λ _sp is 606 nm voor de Au/air-interface [12, 36]. De straal van de linker en rechter halfronde spleten zijn 5 m en 4,697 m. De genormaliseerde transversale en longitudinale distributies van de SPP-focussen worden geëxtraheerd en vergeleken in Fig. 2g en h. De spin-afhankelijke transversale verschuivingen van de SPP-focussen in Fig. 2a-d verdwijnen. De posities en de profielen van de SPP-focussen gegenereerd door LCP- en RCP-licht zijn exact hetzelfde, wat de haalbaarheid van de spin-onafhankelijke plasmonische lens verifieert.

Full-wave numerieke simulaties worden ook uitgevoerd op basis van de eindige-verschillende tijd-domein (FDTD) methode. De parameters worden gelijk gehouden aan die gebruikt in de analytische berekening met het Huygens-Fresnel principe. De gesimuleerde SPP-verdelingen in figuur 3a en b komen goed overeen met de analytische resultaten. De transversale en longitudinale verdelingen in Fig. 3c en d laten zien dat de volledige breedten op half maximum (FWHM) van de focussen langs de x - en y -richting (190 nm en 260 nm) zijn allemaal kleiner dan een halve golflengte. De positie, de FWHM en de intensiteit van de SPP-focussen zijn allemaal onafhankelijk van de spintoestanden van het invallende licht. De SPP's die door de halfronde spleten worden geëxciteerd, zullen tijdens de voortplanting geleidelijk verzwakken. Het voortplantingsverlies wordt veroorzaakt door de absorptie in het metaal [11, 12] en is in de simulaties in aanmerking genomen door gebruik te maken van een complexe permittiviteit (ε _Au = − 11.821 + 1.426i ). Het voortplantingsverlies heeft dus geen invloed op de spinafhankelijke focussering van de SPP's. Figuur 3 e en f geven de faseverdelingen rond het brandpunt. Zoals aangegeven door de groene gestippelde pijlen, balanceren twee spiraalfasen met de klok mee en tegen de klok in tegen elkaar, wat leidt tot de spin-onafhankelijke SPP-focussering. De vlakke fase in het midden komt overeen met het scherpstelgebied. Opgemerkt moet worden dat de faseverdelingen van SPP's in Fig. 3e en f verschillend zijn onder verschillende spintoestanden van het excitatielicht. Maar ze zijn centrale symmetrie, wat vereist dat de intensiteitsverdelingen van SPP's ook centrumsymmetrie moeten zijn. Om te voldoen aan de eis van centrumsymmetrie, moeten de SPP-focussen die worden gegenereerd door LCP en RCP-licht beide in het midden worden geplaatst. De spin-onafhankelijke intensiteitsverdelingen betekenen dus niet noodzakelijk dat de faseverdelingen spin-onafhankelijk zijn. Hier verwijzen we vooral naar de veldintensiteit als we zeggen spin-onafhankelijk.

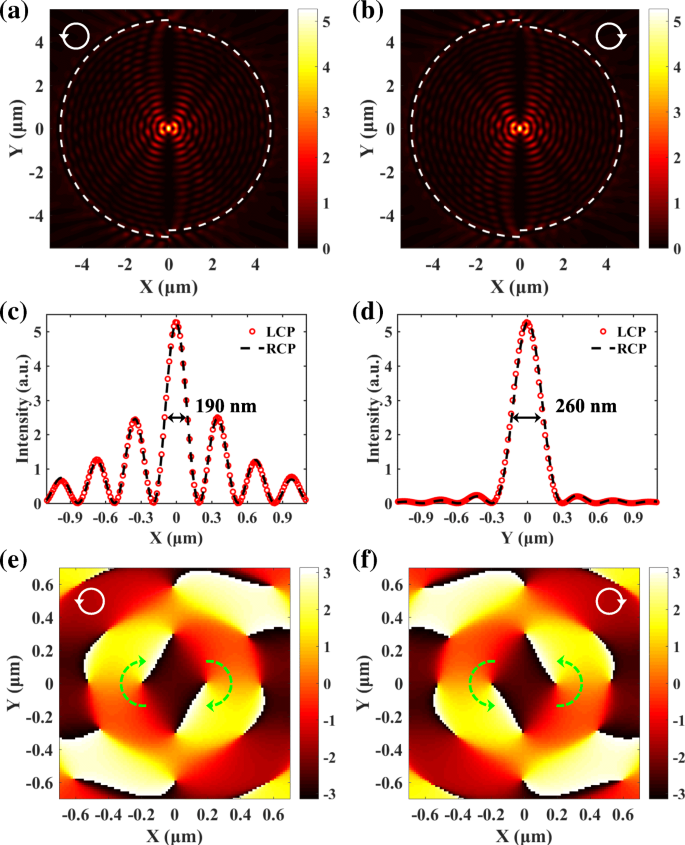
Gesimuleerd SPP-veld gegenereerd door LCP (a ) en RCP (b ) licht. c , d De bijbehorende transversale en longitudinale verdelingen. De posities en profielen van de SPP-focussen die worden gegenereerd door LCP en RCP-licht zijn precies hetzelfde. e , v De bijbehorende faseverdelingen rond het brandpunt. De twee spiraalfasen met tegengestelde richtingen in e en f kunnen elkaar opheffen, wat de oorsprong is van spin-onafhankelijke SPP-focussering

De evoluties van de SPP-verdeling met het verschil in straal Δr worden onthuld. Wanneer de stralen voldoen aan Δr = nλ _sp , zijn de twee halfronde spleten gelijk aan één cirkelvormige spleet met een spiraalvormige fase variërend van 0 tot 2π . r . nemen = λ _sp als voorbeeld kunnen de spinafhankelijke SPP-vortexen worden verkregen, zoals weergegeven in Fig. 4a en b. De faseverdelingen in de inzet van figuur 4a en b laten zien dat de topologische lading van SPP-vortexen l is = 1 en l =1 voor respectievelijk LCP- en RCP-licht. Dus de scheiding Δr tussen de twee halfronde spleten heeft een grote invloed op de prestatie van de plasmonische lens. De twee spiraalfasen kunnen elkaar opheffen, en spin-onafhankelijke SPP-focussering kan alleen worden bereikt als Vgl. (6) is tevreden. Bovendien, volgens vgl. (6), de straal en de centrale hoek van de spleten konden de focusserende eigenschap van de plasmonische lens niet beïnvloeden. Voor boogspleten met een centrale hoek 2π /3, r ₁ =3.7 μm en r ₂ =2.2 μm, $ \Delta r=\frac{5}{2}{\lambda}_{\mathrm{sp}} $, en de SPP's die worden opgewekt door LCP- en RCP-licht zijn allemaal gefocust in het centrum, zoals getoond in Fig. 4c en d. Bovendien kan de voorgestelde benadering worden toegepast op de spiraalspleten. Voor een spiraalvormige spleet beschreven door $ {r}_1\left(\theta \right)={r}_0+\frac{\theta }{\pi }{\lambda}_{\mathrm{sp}} $, nog een spiraalvormige spleet toevoegen met r ₂ = r ₁ − λ _sp /2 kan de spiraalfase compenseren en spin-onafhankelijke SPP-focussering realiseren. De SPP-verdelingen in figuur 4e en f demonstreren de veelzijdigheid en robuustheid van de voorgestelde aanpak.

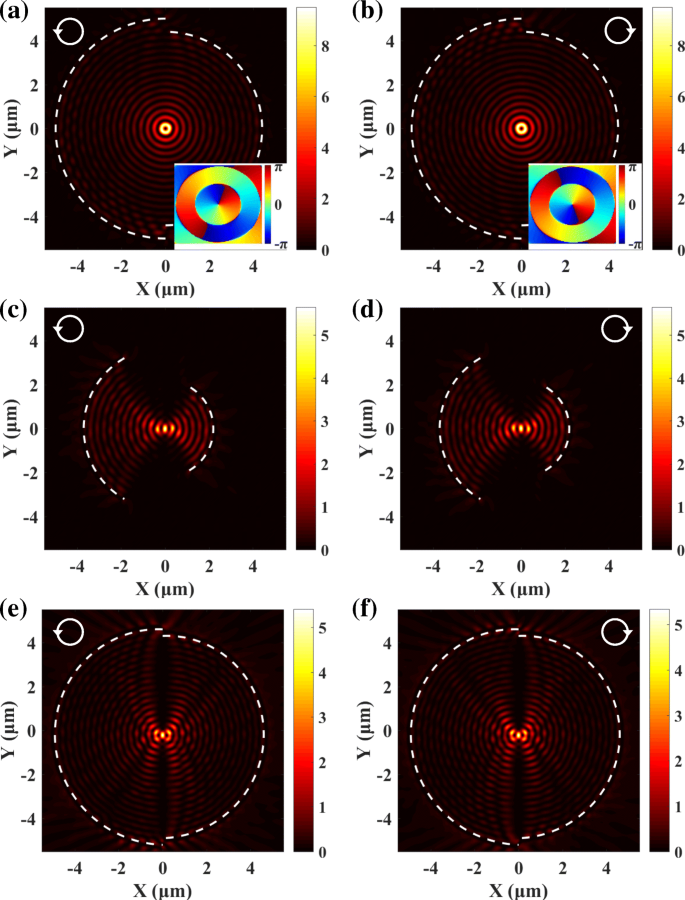
Voor halfronde spleten met Δr = λ _sp , SPP-vortexen opgewekt door LCP (a ) en RCP (b ) vertonen tegengestelde topologische ladingen. De verandering van de straal en de centrale hoek heeft geen invloed op de spin-onafhankelijke SPP-focussering (c , d ). De voorgestelde aanpak is ook geschikt voor spiraalvormige sleuven (e , v )

Spin-onafhankelijke SPP-focussering op basis van Pancharatnam-Berry Phase

In de bovenstaande discussies hebben we de halfronde spleet als geheel behandeld. Zoals weergegeven in figuur 5a, kan een halfronde spleet worden verdeeld in rechthoekige sleuven onder de golflengte. Op deze manier wordt de geometrie Pancharatnam-Berry (PB) fase bepaald door de oriëntatiehoek van de spleet ingebracht [37, 38], die kan worden uitgedrukt als φ _PB = σ _m α . De fase van SPP's gegenereerd door elke subgolflengtespleet is dus:

$$ {\Phi}_{\mathrm{sp}}\left(\theta \right)={\sigma}_{\pm}\theta +{\varphi}_{\mathrm{PB}}. $$ (7)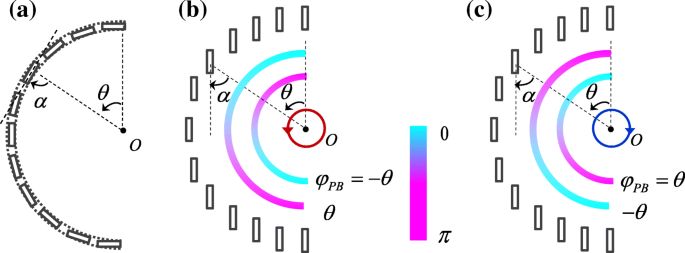

Een halfronde spleet kan worden onderverdeeld in rechthoekige sleuven onder de golflengte (a ). Wanneer de spleten verticaal zijn gerangschikt, kan de PB-fase die door elke spleet wordt gegenereerd, worden gebruikt om de spiraalvormige fasen die door het LCP worden gegenereerd, lokaal op te heffen (b ) en RCP-lampje (c )

De spiraalfase kan lokaal worden opgeheven door de PB-faseverdeling te sturen. In Fig. 5a is de PB-fase een constante φ _PB = π /2 en heeft geen effect op de spiraalfase. Wanneer de PB-fase voldoet aan φ _PB = σ _m θ , wordt de spiraalfase lokaal gecompenseerd en de fase van SPP's die door elke spleet worden gegenereerd, is Φ_sp (θ ) = 0. De subgolflengtespleten moeten dus in verticale richting worden uitgelijnd, zoals weergegeven in figuur 5b en c.

De intensiteitsverdelingen van SPP's gegenereerd door de spin-onafhankelijke plasmonische lens, bestaande uit verticale subgolflengtespleten, worden gegeven in Fig. 6a en b. De breedte en lengte van de sleuven zijn respectievelijk 50 nm en 200 nm. De longitudinale en transversale profielen van de SPP-focussen in Fig. 6c en d laten zien dat de positie, de FWHM en de intensiteit van de SPP-focussen gegenereerd door het LCP- en RCP-licht niet te onderscheiden zijn. Vergeleken met de SPP-verdelingen in figuur 3c en d, is de transversale FWHM van de focus ongeveer hetzelfde, terwijl de longitudinale FWHM meer dan drie keer groter is. Dat komt omdat SPP's gegenereerd door de tegenovergestelde halfronde spleet in Fig. 3c en d de transversale grootte van de SPP-focus effectief kunnen comprimeren. Figuur 6 e en f tonen uniforme hoekfaseverdelingen rond de focus en er wordt geen spiraalvormige fase waargenomen. Dat komt doordat de spiraalfase plaatselijk is opgeheven door de PB-fase. Dit is duidelijk anders dan de benadering met dubbele halfronde spleten, waarbij nog steeds de spiraalvormige fasen in Fig. 3e en f behouden blijven. De verandering van straal en centrale hoek heeft geen invloed op de scherpstellingseigenschap van de SPP-lens. Figuur 6 g en h tonen de spin-onafhankelijke SPP-verdelingen gegenereerd door spleten met een centrale hoek 2π /3 en straal r = 2 μm.

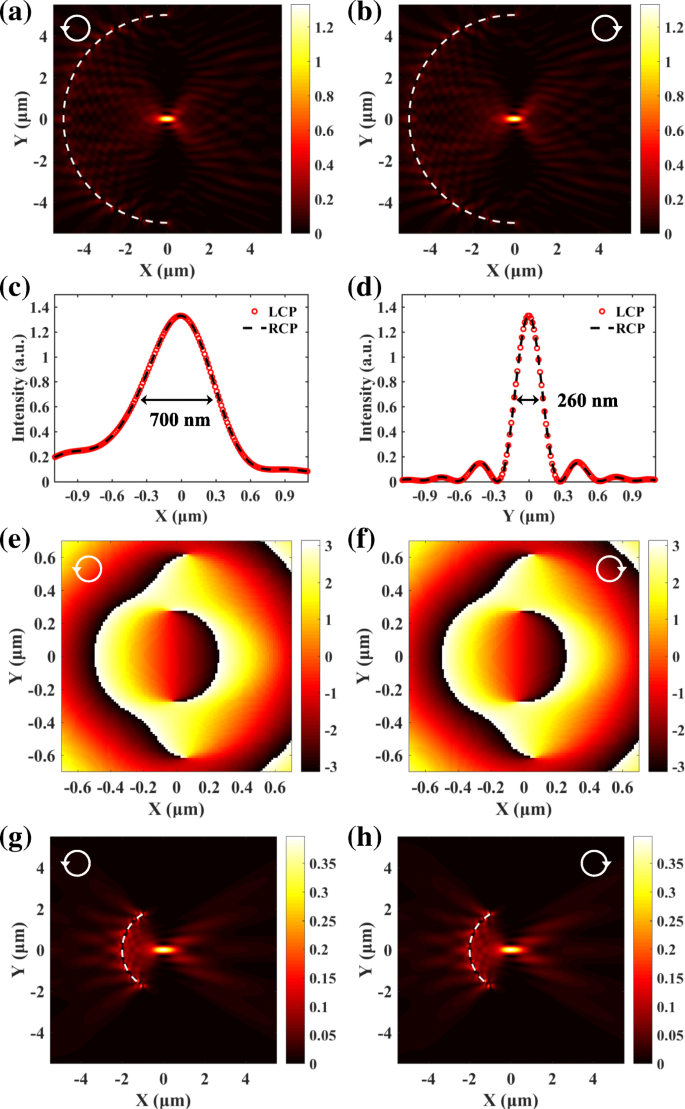
een , b De spin-onafhankelijke SPP-focussering voor de lens bestond uit subgolflengtespleten. c , d De transversale en longitudinale profielen van de SPP focus. e , v De bijbehorende faseverdelingen. g , u De spin-onafhankelijke SPP-focussering kan niet worden beïnvloed door de verandering van de straal en de middelpuntshoek

Conclusies

Concluderend, het tegenwicht bieden aan de spin-afhankelijke spiraalfase door een andere spiraalfase of Pancharatnam-Berry-fase te introduceren, is het fundamentele principe van spin-onafhankelijke SPP-focussering. De posities en profielen van SPP-focussen gegenereerd door LCP- en RCP-licht zijn precies hetzelfde met de spin-onafhankelijke plasmonische lens. Deze studie laat verder zien dat de spiraalfase een beslissende factor is bij het bepalen van de focusseringseigenschap van de halfronde plasmonische lens. Bovendien kunnen de voorgestelde methoden worden gebruikt om polarisatie-onafhankelijke apparaten in andere frequentiebanden [39, 40] te ontwerpen door de structuur te schalen.

Methoden

3D numerieke simulaties worden uitgevoerd met de commerciële software Lumerical FDTD Solutions. In de simulatie worden halfronde spleten met een breedte van 240 nm geëtst op de 150 nm dikke goudfilm en het substraat is SiO₂ met een brekingsindex van 1,46. De brekingsindex van de goudfilm kan worden verkregen uit het Johnson en Christy-model [36]. De mesh-nauwkeurigheid is ingesteld op 3 en de overeenkomstige grootte van elke mesh-cel is ongeveer 13 × 13 × 40 nm, wat een goede afweging kan maken tussen nauwkeurigheid, geheugenvereisten en simulatietijd. Perfect op elkaar afgestemde lagen (PML) met acht aantallen lagen in de x -, j -, en z -richtingen worden gebruikt als randvoorwaarden om de zich voortplantende SPP-velden op te vangen. Horizontaal gepolariseerd licht en verticaal gepolariseerd licht met een andere fase σ _± π /2 worden gebruikt om de LCP- en RCP-lichtbronnen te synthetiseren. En de lichtbron verlicht het monster vanaf de achterkant om zijn invloed op de opgewonden SPP's te vermijden. Om de profielen van SPP-focus te verkrijgen, wordt een 2D-veldmonitor 50 nm boven de goudfilm geplaatst, wat binnen de vervallengte van SPP's ligt.

Afkortingen

FDTD:: Eindig-ander tijddomein
FT:: Fourier-transformatie
FWHM:: Volledige breedte op halve maximum
LCP-lampje:: Links circulair gepolariseerd licht
PB-fase:: Pancharatnam-Berry-fase
RCP-lampje:: Rechts circulair gepolariseerd licht
ZIJ:: Spin Hall-effect
SPP's:: Oppervlakte plasmon polaritonen

Bidegradatiebeoordeling van poly (melkzuur) gevuld met gefunctionaliseerde Titania-nanodeeltjes (PLA/TiO2) onder compostomstandigheden Vervaardiging van NiO/NiCo2O4-mengsels als uitstekende microgolfabsorbers

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal