Plasmonische chirale metasurface-absorber gebaseerd op dubbellaagse viervoudig gedraaide halve cirkel nanostructuur met optische frequentie
Abstract
In dit artikel presenteren we een plasmonische chirale metasurface absorber (CMSA), die een hoge selectieve absorptie kan bereiken voor rechtshandige en linkshandige circulaire polarisatie (RCP, "+" en LCP, "−") lichten op optische frequentie. De CMSA is samengesteld uit een diëlektrisch substraat ingeklemd met een dubbellaagse viervoudig gedraaide halve cirkel metalen nanostructuur. De voorgestelde CMSA heeft een sterke selectieve absorptieband, waar absorptiepieken voor LCP- en RCP-lampen optreden bij verschillende resonantiefrequenties, wat het bestaan van een significant circulair dichroïsme (CD) effect weerspiegelt. Het is aangetoond dat de absorptie van de CMSA kan oplopen tot 93,2% voor LCP-licht en 91,6% voor RCP-licht, en de maximale CD-magnitude is maximaal 0,85 en 0,91 rond respectievelijk 288,5 THz en 404 THz. Het mechanisme van de sterke chiroptische respons van de CMSA wordt geïllustreerd door elektrische veldverdelingen van de eenheidscel-nanostructuur. Verder wordt de invloed van de geometrie van de voorgestelde CMSA op de circulaire polarisatie selectieve absorptiekarakterisering systematisch bestudeerd.
Inleiding
Chiraliteit, als een alomtegenwoordig fenomeen dat verwijst naar een geometrische eigenschap van een object zonder enige inversie of spiegelvlaksymmetrie, blijft altijd relevant voor wetenschap en technologie [1, 2]. Chirale media verschijnen meestal in twee enantiomere vormen die spiegelsymmetrisch zijn en niet op hun spiegelbeeld kunnen worden gesuperponeerd door eenvoudige translatie of rotatie, en ze vertonen altijd een verschillende respons op rechtshandige en linkshandige circulaire polarisatie (RCP, "+", en LCP, “−”) licht [1]. Circulair dichroïsme (CD) van circulair polarisatie (CP) licht afkomstig van chirale media is een van de meest unieke chiroptische eigenschappen. Het CD-effect verwijst naar een verschillende respons van de RCP- en LCP-lichten in chirale media die brede toepassingsmogelijkheden hebben in de biologie, medische wetenschap, chemie, evenals polarisatiegerelateerde opto-elektronische apparaten [3,4,5]. Het CD-effect van natuurlijke materialen is echter nogal zwak, wat de praktische toepassing ervan extreem belemmert. Meta-oppervlakken, als een subklasse van metamaterialen bestaande uit een monolaag of een paar lagen vlakke structuren, zijn veelbelovend voor willekeurige elektromagnetische (EM) golf- of lichtmanipulatie [6,7,8,9,10]. In het bijzonder kan chiraal metasurface (CMS) de chirale optische effecten met verschillende ordes van grootte versterken.
De CMS'en hebben enorme belangstelling gekregen omdat het exotische EM-eigenschappen zou kunnen vertonen, waaronder negatieve brekingsindex en optische activiteit [11, 12], asymmetrische transmissie [13, 14], gigantisch CD-effect [15,16,17], polarisatieconversie [18, 19], en golffrontmanipulatie [20, 21] enz. Sindsdien zijn verschillende CMS-structuren (zoals split-ring, spiraaldraad, gammadion, L-vormig enzovoort) achtereenvolgens voorgesteld om zeer efficiënte chirale selectieve veldverbetering voor LCP- of RCP-licht [22,23,24,25,26,27,28,29,30,31,32,33]. De meeste eerdere ontwerpen van die CMS zijn echter gericht op de prestaties van chiraliteit bij transmissie, terwijl er veel minder aandacht is besteed aan de reflectie / absorptie voor CP-lampen, die even belangrijk zijn in technische toepassingen. Het is algemeen bekend dat de meeste studies van eerdere absorbers worden toegepast op lineair polarisatielicht, terwijl dergelijke ontwerpen voor CP-lampen zelden worden bestudeerd. In feite zouden de CMS'en ook kunnen worden gebruikt om nieuwe absorbers voor CP-lampen te construeren [25, 26, 29,30,31,32,33]. Bijvoorbeeld, Li et al. [25] stelde een ultradunne absorber voor op basis van de L-vormige draden, die de LCP-golf alleen in het microgolfgebied kan verzwakken. Wang et al. [29] toonde aan dat een chirale metamirror bijna al het LCP-licht kan reflecteren, terwijl het RCP-licht in het infraroodgebied volledig wordt geabsorbeerd. Tang et al. [30] stelde een absorber voor met ŋ-vormige resonatoren, die selectieve absorptie voor verschillende CP-lichten in zichtbaar kan bereiken. Vervolgens zijn nabij-infrarood chirale absorptiemiddelen met plasmonisch meta-oppervlak voorgesteld en aangetoond dat ze selectief LCP- of RCP-licht absorberen. De absorptie van de meeste CMS'en is echter minder dan 90%. Een effectief ontwerp van de chirale metasurface absorber (CMSA) met de hoge selectieve absorptie is dus zeer wenselijk.
In dit werk presenteren we een soort zeer efficiënte CMSA op basis van een dubbellaagse viervoudig gedraaide halve cirkel nanostructuur die werkt in nabij-infrarood en zichtbaar gebied. Een dergelijke CMSA zou selectief meer dan 90% absorptie kunnen bereiken voor CP-lampen met verschillende handen bij verschillende resonantiefrequenties. Door de sterke selectieve absorptie van de voorgestelde CMSA kan dienovereenkomstig een hoge CD-waarde van ongeveer 0,9 worden gerealiseerd. Het fysieke mechanisme dat ten grondslag ligt aan selectieve absorptie voor verschillende CP-lampen is in detail geanalyseerd door elektrische veldverdelingen. Bovendien zijn de invloeden van geometrische eenheidscelparameters op selectieve absorptie ook systematisch bestudeerd. Er kan redelijkerwijs worden aangenomen dat de resultaten in dit werk als leidraad kunnen dienen voor het ontwerp van CMSA met sterke absorptie en CD-effect voor veel praktische toepassingen, zoals thermische absorptiemiddelen, optische communicatieapparatuur, fotodetector, optische filters, beeldvorming en hologrammen.
Eenheidcelontwerp
Figuur 1 geeft het schematische diagram weer van de voorgestelde CMSA, die is gemaakt van een periodieke array met een gedraaide halve cirkel nanostructuur. De viervoudig gedraaide halve cirkel nanostructuur aan elke kant van het diëlektrische substraat is zo gepositioneerd dat elk met 90 ° is geroteerd ten opzichte van zijn buur, en aan de onderkant wordt elke halfronde nanostructuur ook 90 ° gedraaid ten opzichte van de bovenste, zoals weergegeven in afb. 1b. Net als bij het vorige ontwerp [32] zijn de bovenste vier halfronde nanostructuren verbonden met de onderste door koperen cilinders, en de straal van de koperen cilinder is hetzelfde als de halve cirkeldraadbreedte, wat de geleidende koppeling kan vergroten. De nanostructuur met gedraaide halve cirkels kan worden gezien als een gekoppeld resonatorsysteem, waarbij de sterke chirale reacties voortkomen uit de elektrische en magnetische inductieve koppeling tussen de twee gedraaide verbonden halve cirkels [34, 35]. Deze eenvoudige gedraaide halve cirkel-nanostructuur met spiegelsymmetrieën is ontworpen in de bovenste en onderste lagen, waardoor de voorgestelde CMSA de chiraliteit kan verbeteren.
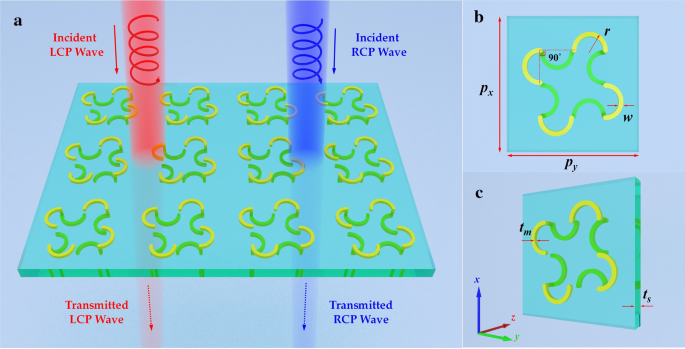
Schema van de ontworpen CMSA:a periodieke reeks, b , c de voor- en perspectivische weergave van de nanostructuur van de eenheidscel. De periodieke lengtes langs x - en y- asrichtingen zijn beide 600 nm, en de normale invallende CP-lichten planten zich voort langs de z -as richting
De totale eenheidscel van de voorgestelde CMSA vertoont een viervoudige rotatie (C4 ) symmetrie voor de voortplantingsrichting van het licht. Het diëlektrische substraat in de middelste laag is gemaakt van een verliesvrij diëlektrisch MgF2 met een relatieve permittiviteit van 1,9. De chirale metalen nanostructuren werden geselecteerd als goud en de materiaalparameter kan worden beschreven door het Drude-model [36]. De geoptimaliseerde structuurparameters van de eenheidscel worden gegeven als:p x = p j = 600 nm, r = 70 nm, w = 40 nm, t s = 120 nm, t m = 30 nm. De eenheidscel van de CMSA is periodiek langs de x- en y -asrichtingen met de perioden van 600 nm om diffractie te vermijden wanneer de lichtfrequentie van de inval tot 500 THz komt. Om de efficiëntie van de voorgestelde CMSA te verifiëren, werden de full-wave hoogfrequente EM-simulaties uitgevoerd op basis van de eindige-elementenmethode (FEM) met behulp van de frequentiedomeinoplosser in CST Microwave Studio. Zodra de CMSA-eenheidscel-nanostructuur, de juiste randvoorwaarden, maaswijdte en frequentiebereik redelijk zijn ingesteld, kan de simulatie van het frequentiedomein worden gestart.
Resultaten en discussies
De gesimuleerde co-polarisatie transmissiecoëfficiënten (t ++ (ω), t − − (ω)) en reflectiecoëfficiënten (r ++ (ω), r − − (ω)) voor normaal invallend LCP- en RCP-licht worden weergegeven in Fig. 2. Twee chirale plasmonische resonantiemodi (modus 1 en modus 2) konden duidelijk worden waargenomen bij frequenties van f 1 = 288.5 THz en f 2 = 404 THz, respectievelijk. Opgemerkt kan worden dat de co-polarisatie reflectiecoëfficiënt r ++ (ω) voor RCP en r − − (ω) voor LCP-lampen zijn gelijk; en beide zijn minder dan 0,4 in het hele geïnteresseerde frequentiebereik. Bovendien zijn de magnitudes van r ++ (ω) en r − − (ω) afname tot ongeveer 0,15 bij resonanties, wat de impedantie-overeenkomst aangeeft tussen de CMSA en de vrije ruimte voor zowel RCP- als LCP-lampen. Het is ook te zien dat de co-polarisatie transmissiecoëfficiënten t ++ (ω) voor RCP en t − − (ω) voor LCP-lampen zijn significant verschillend bij resonanties vanwege de chirale aard van de voorgestelde CMSA. Rond het lagere frequentiepunt f 1 , de grootte van t ++ (ω) voor het RCP-licht is ongeveer 0,93, wat veel hoger is dan t − − (ω) voor het LCP-licht dat ongeveer slechts 0,075 is. Rond het hogere frequentiepunt f 2 , de grootte van t ++ (ω) voor het RCP-licht neemt af tot een minimale waarde van 0,018, terwijl t − − (ω) voor de LCP is tot de maximale waarde van ongeveer 0,92. Dit betekent dat alleen het invallende RCP-licht kan worden geselecteerd om door de CMSA te gaan, terwijl het LCP-licht op de lagere frequentie verboden is. Zoals bij de hogere frequentie f 2 , alleen het invallende LCP-licht kan worden geselecteerd om door de CMSA te gaan, terwijl het RCP-licht uiterst verboden is. De chirale selectiefenomenen van de CMSA hierboven zouden bijgevolg resulteren in de verschillende absorptie voor de RCP- en LCP-lampen, wat het bestaan van een zeer efficiënte selectieve absorptie en een gigantisch CD-effect bij resonanties impliceert.
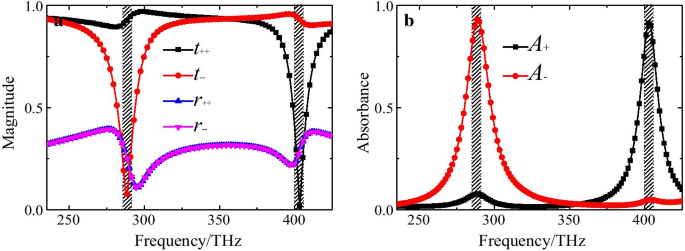
een Gesimuleerde co-polarisatie transmissiecoëfficiënten (t ++ (ω), t − − (ω)) en reflectiecoëfficiënten (r ++ (ω), r − − (ω)) van de voorgestelde CMSA voor de normale invallende LCP- en RCP-lichten, b de bijbehorende absorptie (A + (ω), A − (ω)) voor zowel LCP- als RCP-lampen
Figuur 2b toont de absorptiespectra (A + (ω), A − (ω)) voor zowel invallende LCP- als RCP-lichten. Er kan worden waargenomen dat de absorptie voor LCP- en RCP-lampen een maximale waarde heeft van ongeveer 93,2% en 91,6%, terwijl die voor RCP- en LCP-lampen is afgenomen tot slechts ongeveer 8,7% en 4,8% rond de bovenstaande twee resonanties, respectievelijk . Vanzelfsprekend kan worden geconcludeerd dat de voorgestelde CMSA een sterke absorptie van LCP-licht vertoont en een vrij hoog transmissieniveau voor het RCP-licht rond de lagere frequentie f 1 , terwijl de toestand volledig omkeert wanneer de frequentie de hogere resonantiefrequentie f . bereikt 2 . Het betekent dat de voorgestelde CMSA een selectieve absorptie vertoont voor twee CP-lampen met een bijzondere handigheid, terwijl de andere met verschillende resonanties wordt gereflecteerd. Bovendien is het ook de moeite waard om te benadrukken dat de CMSA de twee sterke absorptiefrequentiebanden heeft die slechts één chirale nanostructuur van één grootte gebruiken, en redelijk superieur is in vergelijking met de vorige chirale absorbers met één geïsoleerde absorptieband waarvan de aanpassing voor ander CP-licht sterk afhankelijk is van verschillende geometriegrootte [25, 26, 29, 31,32,33]. De ontworpen chirale nanostructuur kan dus dienen als een perfecte LCP-lichtabsorbeerder bij de lagere frequentie en een perfecte RCP-lichtabsorbeerder bij de hogere frequentie. Opgemerkt moet worden dat de selectieve absorptieprestatie van de voorgestelde CMSA zal verslechteren met de toename van de invalshoek (schuine inval), vanwege de multipolaire plasmonresonantie van hogere orde (niet getoond). Verder kan worden afgeleid dat de hoge chiraal-selectieve absorptie voor CP-lampen zal resulteren in een gigantisch CD-effect in voorgestelde CMSA.
Het verschil in absorptie of transmissie tussen de LCP- en RCP-lampen kan worden gekarakteriseerd door de CD-parameter Δ . Figuur 3a geeft het CD-spectrum van de CMSA weer, waarbij de belangrijkste pieken van de CD-parameter respectievelijk ongeveer 0,85 en 0,91 zijn bij twee resonantiefrequenties; wat veel groter is dan de gerapporteerde chirale nanostructuren [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32, 37,38,39,40, 41,42]. Het gigantische CD-effect wordt veroorzaakt door de sterke chiraliteit van de CMSA en kan daarom worden toegepast als een transparante circulaire polarisator. Om de CP-zuiverheid van de CMSA toegepast als circulaire polarisator verder te onderzoeken, geven we de ellipticiteitshoek η en polarisatie azimut rotatiehoek θ zoals getoond in Fig. 3b. Het kan worden gevonden dat de waarde van η is ongeveer 40,4° en − 43,9°, terwijl de waarde van θ is ongeveer 0° bij respectievelijk de lagere en hogere frequenties. Het betekent dat de doorgelaten lichten prominente RCP- en LCP-kenmerken vertonen nadat ze door de CMSA-plaat zijn gegaan bij de twee resonantiefrequenties. Opgemerkt moet worden dat deze op CMSA gebaseerde circulaire polarisator met de hogere CP-zuiverheid geldig is voor willekeurig gepolariseerde lichten vanwege de hoge C4 symmetrie van de eenheidscel. Er kan dus redelijkerwijs worden aangenomen dat de homogene circulaire polarisator wordt gerealiseerd met onze ontworpen chirale nanostructuur.
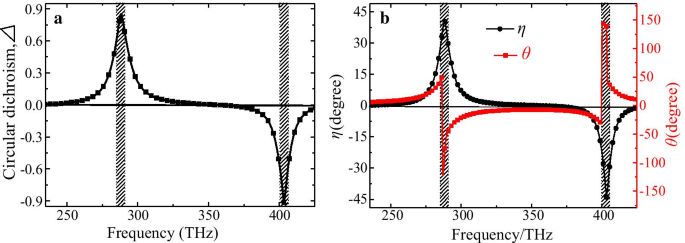
De berekende relatieve optische parameters van de voorgestelde CMSA voor de normale invallende LCP- en RCP-lichten, a de CD-parameter Δ , b ellipticiteitshoek η en polarisatie azimut rotatiehoek θ
Om de selectieve absorptie en het gigantische CD-effect van de CMSA volledig te begrijpen, hebben we de brekingsindex Re(n ), Re(n − ), Re(n + ) en chirale parameter Re(κ ) met behulp van een standaard ophaalprocedure van de transmissie- en reflectiecoëfficiënten van CP-lampen [43, 44], zoals getoond in Fig. 4a, b. Het is duidelijk dat twee resonanties gerelateerd aan de sterke chiraliteit naar voren komen in de ontworpen CMSA. De resonantie van de lagere frequentie vindt plaats rond 288,5 THz, terwijl de hogere resonantie zich bij 404 THz bevindt, wat consistent is met de karakteristieke frequenties van selectieve absorptie en CD-pieken. Zoals getoond in Fig. 4a, is de Re(n ) is negatief met maximale magnitudes van -2,3 en -1,1, en de Re(κ ) is tot maximale magnitudes van 6,4 en -5,1 rond de twee resonantiefrequenties hierboven. Het is duidelijk dat de chirale parameter κ draagt ook bij aan de negatieve breking van RCP- en LCP-lampen. Door de sterke chiraliteit kan de brekingsindex van het RCP/LCP-licht gemakkelijk negatief worden bij resonanties vanwege de relatie van n ± = n ± κ . Dus, zoals getoond in Fig. 4b, de Re(n − ) voor LCP-licht en Re(n + ) voor RCP-licht is negatief van respectievelijk 286,2 THz tot 291 THz en 400,2 THz tot 404 THz. Bovendien is de Re(n − ) en Re(n + ) zijn tot de maximale negatieve waarden van -8,6 en -6,3 bij respectievelijk twee resonanties hierboven. Het onthult dat de hoge selectieve absorptie en het gigantische CD-effect van de voorgestelde CMSA geassocieerd zijn met de negatieve brekingseigenschap van de LCP- en RCP-lampen.
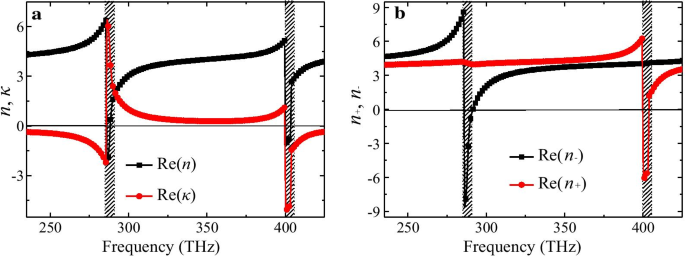
De opgehaalde relatieve chirale parameters van de voorgestelde CMSA:a reële delen van de gemiddelde brekingsindex Re(n ) en chirale parameter Re(κ ), b brekingsindex Re(n − ), Re(n + ) voor LCP- en RCP-lampen
Om de oorsprong van de selectieve absorptie in verband met het gigantische CD-effect van de voorgestelde CMSA verder te onthullen, wordt het elektrische veld (E z ) distributies van de eenheidscel aangedreven door RCP- en LCP-lampen bij 288,5 THz en 404 THz zijn bestudeerd. Het is bekend dat de excitatie van oppervlakteplasmonresonantie oscillerende dipoolvelden zal produceren, aangezien de halfronde nanostructuur kleine diameters vertoont in vergelijking met de invallende golflengte van de verschillende CP-lampen [45,46,47,48]. Wanneer RCP- of LCP-licht op de halfronde nanostructuur schijnt, kan redelijkerwijs worden aangenomen dat de selectieve absorptie en het gigantische CD-effect zullen optreden in de voorgestelde CMSA en bijgevolg resulteren in de verschillende distributie van het elektrische veld en magnetische veldcomponenten in elke laag [48] ,49.50.51.52.533].
Figuur 5 toont het elektrische veld (E z ) distributies van de voorgestelde CMSA aangedreven door RCP- en LCP-lampen bij verschillende resonantiefrequenties. De detailgrafieken van het elektrische veld (E z ) distributies op de halve cirkel nanostructuren tonen duidelijk de aard van elke sruface plasmonics-modus [54]. Het rode en blauwe gebied op de halfronde nanostructuur van de bovenste en onderste lagen presenteert de positieve en negatieve ladingsaccumulaties onder RCP- en LCP-lichtexcitatie. De positieve en negatieve ladingen zijn gescheiden en voornamelijk geaccumuleerd in de hoeken van de nanostructuur van elke halve cirkel, en werken als een elektrische dipooloscillatie. Het kan worden waargenomen dat het elektrische dipoolvermogen veel sterker is dan het magnetische in de ontworpen halve cirkel-nanostructuur, wat het overwicht van elektrische dipooloscillaties onthult. De selectieve absorptie en het gigantische CD-effect dat wordt gegenereerd bij resonanties is te wijten aan het duidelijke dipoolvermogen dat verschilt onder LCP- en RCP-excitatie. Hier is een vereenvoudigde methode met equivalente elektrische dipoolmomenten toegepast, die de ladingstrillingen van vier halfcirkelvormige nanostructuren in elke laag als één dipooltrilling beschouwt [48,49,50]. Volgens de Born-Kuhn-theorie [47, 48] wordt de modus die wordt gehybridiseerd uit twee dipolen met dezelfde elektrische veldrichting de bindingsmodus genoemd, terwijl de andere modus die wordt gehybridiseerd uit twee dipolen met 90 ° of dwarsrichting wordt aangeduid als antibonding-modus. Zoals getoond in Fig. 5a1, b1, onder RCP-lichtverlichting met een resonantiefrequentie van f 1 = 288.5 THz, de elektrische dipoolvelden in de bovenste en onderste lagen tonen de dwarsrichtingen en vormen een antibonding-modus, wat resulteert in de hoge transmissie van RCP-licht volgens het Born-Kuhn-model. Zoals getoond in Fig. 5c1, d1, onder LCP-lichtverlichting, kan worden gezien dat de elektrische veldverdeling van CMSA kan worden beschouwd als een hybride van de bindingsmodus tussen de bovenste en onderste lagen, die is samengesteld uit twee equivalente elektrische dipoolmomenten met dezelfde richting, wat resulteert in een hoog absorptieniveau van LCP-licht. De bindings- en antibindingsmodi veroorzaken dus verschillende resonantie-energie en verschillende transmissie en absorptie van chirale nanostructuren bij de lagere frequentie onder LCP- en RCP-lichtverlichting (zie figuur 2). Zoals getoond in Fig. 5a2, b2, c2, d2, onder RCP en LCP lichten verlichting op resonantiefrequentie van f 2 = 404 THz, de elektrische dipoolvelden in de bovenste en onderste lagen vertonen respectievelijk dezelfde richtingen (bonding-modus) en dwarsrichtingen (antibonding-modus), wat resulteert in een hoog absorptieniveau voor RCP-licht en een hoge transmissie voor LCP-licht. Daarom kan worden gezien dat de selectieve absorptie en het CD-effect bij twee verschillende frequenties voornamelijk worden toegeschreven aan de bindings- en antibonding-modi, die worden veroorzaakt door hybride koppeling van de elektrische dipoolmomenten van de bovenste en onderste laag.
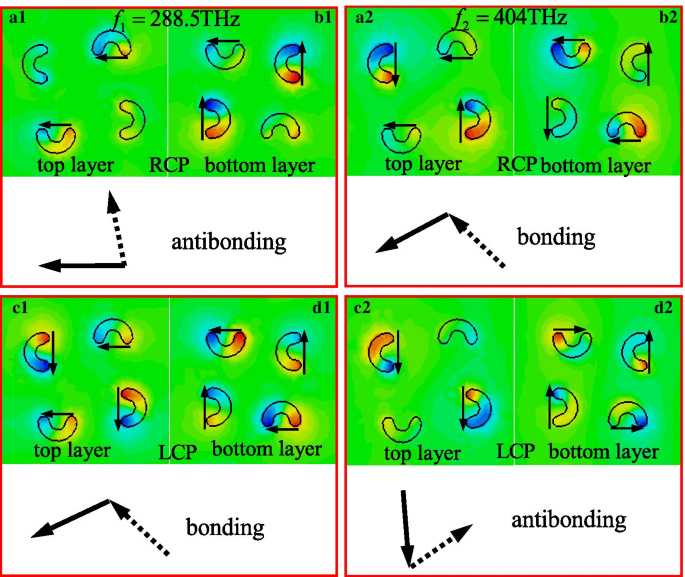
Het elektrische veld (E z ) verdelingen van eenheidscellen van de voorgestelde CMSA geïnduceerd door de (a1 , b1 , a2 , b2 ) RCP en (c1 , d1 , c2 , d2 ) LCP licht op bij verschillende resonantiefrequenties:(a1 –d1 ) f 1 = 288.5 THz, (a2 –d2 ) f 2 = 404 THz. De zwarte ononderbroken lijn (stippellijn) pijlen geven de equivalente elektrische dipoolmomenten aan op de bovenste (onderste) laag van de voorgestelde chirale nanostructuur
In het volgende onderzoeken we de invloeden van de geometrische parameters van de eenheidscel op de absorptie-eigenschappen van de voorgestelde CMSA. Afbeelding 6 toont de gesimuleerde absorptiespectra voor LCP- en RCP-lampen en resonantiefrequenties (f − , f + ) met verschillende geometrische parameters (r , w , t m , en t s ) van de eenheidscel. Voor de ontworpen nanostructuur kon een interessante spectrale variatie van parameterafhankelijke selectieve absorptie-eigenschappen worden waargenomen, die duidelijk multi-factoren competitief en complex is. In deze studie zijn de geometrische parameters van de controlegroep r = 70 nm, w = 40 nm, t m = 30 nm, en t s = 120 nm, en één parameter tegelijk wijzigen.
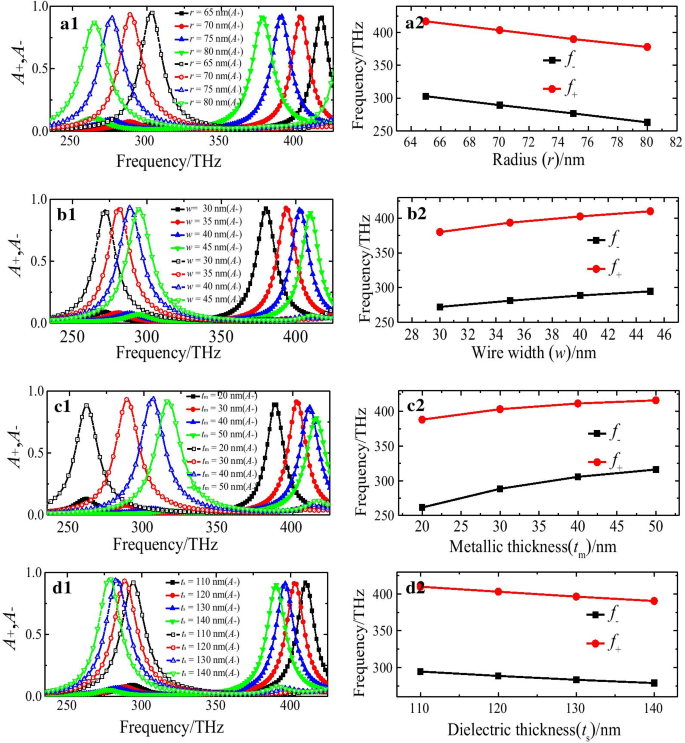
De gesimuleerde (a1 –d1 ) absorptiespectra en (a2 –d2 ) resonantiefrequenties (f − , f + ) van de LCP- en RCP-lampen van de voorgestelde CMSA met verschillende geometrische parameters:(a1 , a2 ) straal (r ), (b1 , b2 ) draadbreedte (w ), en (c1 , c2 ) dikte (t m ) van halve cirkel nanostructuur, (d1 , d2 ) dikte van diëlektrisch substraat (t s )
De halve cirkel nanostructuur met de verschillende r (r = 65 nm, 70 nm, 75 nm en 80 nm) werden eerst berekend, terwijl de andere parameters zijn vastgesteld zoals weergegeven in Fig. 6a1, a2. Wanneer verhoogt r , de resonantiefrequenties f − voor LCP en f + voor RCP-lichten nemen geleidelijk af, wat kan worden geïnterpreteerd door de equivalente LC resonantiekringtheorie [55, 56]. De resonantiefrequenties (f − , f + ) voor zowel LCP- als RCP-lampen kan de verlichting worden uitgedrukt als \(f_{ \mp } =\frac{1}{{2\pi \sqrt {LC} }}\), waarbij equivalente capaciteit C en inductie L worden voornamelijk bepaald door de geometrische parameters van de voorgestelde CMSA. De L zal toenemen met de toename van de r , waardoor de resonantiefrequenties afnemen (f − , f + ). Bovendien, zoals getoond in Fig. 6a1, wanneer verhogingen r , zal de absorptie van het LCP-licht geleidelijk afnemen, terwijl dat van het RCP-licht vrijwel ongewijzigd zal blijven. Afbeelding 6b1, b2 toont de absorptiespectra van de LCP- en RCP-lampen bij het wijzigen van de w van 30 tot 45 nm met een stap van 5 nm, terwijl de andere parameters ongewijzigd blijven. Het is te zien dat de resonantiefrequenties (f − , f + ) voor zowel LCP als RCP lichten zal geleidelijk toenemen met de toename van de w . Het is duidelijk dat de toename van de resonantiefrequenties (f − , f + ) is voornamelijk te wijten aan de daling van de C . De absorptie van het LCP-licht zal eerst toenemen en daarna iets afnemen, terwijl dat van het RCP-licht geleidelijk zal afnemen bij toenemende w , zoals getoond in Fig. 6b2. Zoals getoond in Fig. 6c1, c2, presenteren we de absorptiespectra en resonantiefrequenties (f − , f + ) van de LCP- en RCP-lampen met variërende t m van 20 tot 50 nm door een stap van 10 nm en andere parameters vast. Er zijn vergelijkbare gevallen als de wijziging van w , wanneer verhoogt t m , de resonantiefrequentie (f − ) voor LCP-licht aanzienlijk toenemen, en die voor RCP-licht iets toenemen. In dit geval is de L zal afnemen met het toenemen van de t m , wat resulteert in een toename van de resonantiefrequenties (f − , f + ). Bovendien zal de absorptie van zowel LCP- als RCP-lampen eerst toenemen en vervolgens afnemen bij toenemende t m , zoals getoond in Fig. 6c2. Ten slotte illustreerden we de absorptiespectra en resonantiefrequenties (f − , f + ) voor zowel LCP- als RCP-lampen met verschillende t s (t s = 110 nm, 120 nm, 130 nm en 140 nm), terwijl andere parameters ongewijzigd blijven, zoals weergegeven in Fig. 6d1, d2. Het kan worden opgemerkt dat wanneer verhogingen t s , zal de absorptie van het LCP geleidelijk toenemen, terwijl die van het RCP-licht iets zal afnemen, zoals weergegeven in Fig. 6d1. Bovendien kunnen de resonantiefrequenties (f − , f + ) voor zowel LCP als RCP nemen de lichten geleidelijk af wanneer ze toenemen t s , zoals weergegeven in Fig. 6d2. In dit geval is de C zal toenemen wanneer t . toeneemt s , waardoor de resonantiefrequenties afnemen (f − , f + ). Geconcludeerd kan worden dat de resonantiefrequenties (f − , f + ) en absorptieniveau voor zowel RCP- als LCP-lampen zijn gevoelig voor de geometrische parameters van de eenheidscel van de ontworpen chirale nanostructuur. De selectieve absorptie-eigenschappen van de voorgestelde CMSA kunnen dus dynamisch worden aangepast door structuurparameters te variëren.
Conclusie
Concluderend is een CMSA voorgesteld op basis van een tweelagige viervoudig gedraaide halve cirkel nanostructuur om bijna perfecte chiraal-selectieve absorptie voor RCP- en LCP-lampen te bereiken, evenals een gigantisch CD-effect in zowel nabij-infrarood als zichtbare gebieden. De simulatieresultaten laten zien dat de chiraal-selectieve absorptie voor zowel RCP- als LCP-lampen meer dan 90% is, en dat de CD-magnitude 0,91 kan bereiken. Volgens de teruggevonden effectieve EM-parameters kan worden vastgesteld dat de lagere frequentieabsorptie en het CD-effect beide geassocieerd zijn met de negatieve brekingseigenschappen van het LCP-licht, terwijl het geval van hogere frequentie betrekking heeft op het RCP-licht. De elektrische veldverdelingen geven aan dat de chiraal-selectieve absorptie-eigenschappen en het gigantische CD-effect van de CMSA voornamelijk afkomstig zijn van de bindings- en antibindingsmodi die worden geïnduceerd door hybride koppeling van de elektrische dipoolmomenten van de bovenste en onderste laag. Bovendien kunnen de resonantiefrequenties en het chiraal-selectieve absorptieniveau van de CMSA worden afgestemd door de geometrische parameters van de eenheidscel te wijzigen. Daarom kan redelijkerwijs worden geconcludeerd dat het ontwerp van de CMSA veelbelovend is voor toekomstige toepassingen in optische filters, chirale beeldvorming, circulaire polarisator, detectie en optische communicatie.
Numerieke methode-sectie
FEM-simulaties:Er zijn volledige golf EM-simulaties uitgevoerd op basis van een eindige elementenmethode (FEM). In simulatie worden de elektrische eigenschappen van het goud beschreven door het Drude-model als [36]:
$$\varepsilon_{{{\text{Au}}}} ={1} - \omega_{p}^{{2}} /\omega \left( {\omega + i\gamma } \right)$$ (1)waar ω p = 1.37 × 10 16 rad/s is de plasmafrequentie en γ = 8.04 × 10 13 rad/s is de botsingsfrequentie van het goud in het optische frequentiebereik. In simulatie werd de eenheidscelgrensvoorwaarde toegepast langs x - en y -asrichting en de twee CP eigen lichten werden direct gebruikt. Breedband CP-lampen worden gebruikt als excitatiebronnen en zijn normaal gesproken via de eenheidscel van de ontworpen chirale nanostructuur van de − z naar + z richting. Vervolgens kunnen reflectie- en transmissiecoëfficiënten van zowel LCP- als RCP-lampen worden verkregen. Over het algemeen wordt de absorptie aangeduid als A − (ω)/A + (ω) voor de LCP/RCP-lampen kan worden uitgedrukt als [17, 32]:A − (ω) = 1 − R − − (ω) − T − − (ω) = 1 − |r − − (ω)| 2 − |t − − (ω)| 2 , A + (ω) = 1 − R ++ (ω) − T ++ (ω) = 1 − |r ++ (ω)| 2 − |t ++ (ω)| 2 , respectievelijk. De co-polarisatie transmissiecoëfficiënten t − − (ω) zijn voor de LCP en t ++ (ω) voor de RCP-lampjes, terwijl r − − (ω) en r ++ (ω) zijn respectievelijk de co-polarisatie reflectiecoëfficiënten. Opgemerkt moet worden dat de cross-polarisatie transmissiecoëfficiënten (t +− (ω), t −+ (ω)) en reflectiecoëfficiënten (r +− (ω), r −+ (ω)) voor LCP- en RCP-lampen zijn klein genoeg om te worden verwaarloosd (< 0.01) vanwege de hoge C 4 symmetrie van de eenheidscel van de ontworpen chirale nanostructuur. Bovendien wordt het CD-effect veroorzaakt door de selectieve absorptie van twee CP-lampen, wat kan worden uitgedrukt als:△ =|t ++ (ω)| − |t − − (ω)| [14, 29]. The ellipticity and optical activity are important parameters to evaluate the chirality of the designed chiral nanostructure. The ellipticity characterizes the polarization state of transmitted lights of the chiral nanostructure, which is described by ellipticity angle η = arctan[(|t ++ (ω)| − |t − − (ω)|) / (|t ++ (ω)| +|t − − (ω)|)]. While the optical activity represents the rotation property of polarization plane of a transmitted linear polarization light respect to the incident one, which is described by the polarization azimuth rotation angle θ = [arg(t ++ (ω)) − arg(t − − (ω))]/2.
Availability of data and materials
The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.
Afkortingen
- CMS:
-
Chiral metasurface
- CMSA:
-
Chiral metasurface absorber
- RCP:
-
Right-handed circular polarization
- LCP:
-
Left-handed circular polarization
- CD:
-
Circular dichroism
- EM:
-
Electromagnetic
- CP:
-
Circular polarization
Nanomaterialen
- Optische datacommunicatie
- Optische vezel
- Polarisatie-afhankelijke quasi-ver-veld superfocusstrategie van op nanoring gebaseerde plasmonische lenzen
- Heldere enkelvoudige fotonbron op 1,3 μm gebaseerd op InAs Bilayer Quantum Dot in Micropillar
- Verbeterd niet-lineair optisch effect in hybride vloeibaar-kristalcellen op basis van fotonisch kristal
- Ultra-smalle band Perfect Absorber en zijn toepassing als plasmonische sensor in het zichtbare gebied
- Effecten van dubbellaagse dikte op de morfologische, optische en elektrische eigenschappen van Al2O3/ZnO-nanolaminaten
- Plasmonische sensor op basis van diëlektrische nanoprisma's
- Polarisatieconverter met regelbare dubbele breking op basis van hybride volledig diëlektrisch grafeenmetasurface
- Optisch actieve plasmonische metasurfaces gebaseerd op de hybridisatie van in-plane koppeling en out-of-plane koppeling
- Gemultiplexte optische antennes



