Polarisatie-afhankelijke quasi-ver-veld superfocusstrategie van op nanoring gebaseerde plasmonische lenzen
Abstract
De tweedimensionale superfocussering van op nanoring gebaseerde plasmonische lenzen (NRPL's) voorbij de diffractielimiet in het verre veld blijft een grote uitdaging bij optische golflengten. In dit artikel hebben we, naast de modulatie van structurele parameters, de polarisatie-afhankelijke focusprestaties van een NRPL onderzocht met behulp van de FDTD-methode (finite-difference time-domain). Door gebruik te maken van de staat van polarisatie (SOP) van invallend licht, realiseren we met succes de elliptische, donut- en cirkelvormige brandpunten. De minimale volledige breedte bij half maximum (FWHM's) van deze brandpunten zijn ~0,32, ~0,34 en ~0,42 λ 0 respectievelijk in het totale elektrische veld, en de scherptediepte (DOF) ligt in 1,41~1,77 λ 0 . Deze sub-diffractielimietfoci worden goed gecontroleerd in het quasi-far-field-gebied. Het onderliggende fysieke mechanisme van de focusverschuiving en een effectieve manier om de focuspositie te regelen, worden voorgesteld. Bovendien, in het geval van een hoge numerieke apertuur, bepaalt de longitudinale component, die meer dan 80% van de elektrische veldenergie in beslag neemt, de focusseringspatronen van de brandpunten. De bereikte sub-diffractielimietfocussering kan op grote schaal worden gebruikt voor veel technische toepassingen, waaronder beeldvorming met superresolutie, deeltjesversnelling, kwantumoptische informatieverwerking en optische gegevensopslag.
Achtergrond
Naast de ontwikkeling van beeldvorming met superresolutie [1], deeltjesversnelling [2], kwantumoptische informatieverwerking [3] en polarisatieafhankelijke optische gegevensopslag [4], worden oppervlakteplasmonische apparaten op grote schaal toegepast in deze regio's door het moduleren van de plasmonresonantie in een subgolflengte. De plasmonische lens (PL), als een typisch apparaat, beschikt over de perfecte beeldvormingscapaciteit die voor het eerst werd voorgesteld door J.B. Pendry in 2000 [5], en de optische beeldvorming onder de diffractielimiet werd experimenteel aangetoond door X. Zhang et al. 5 jaar later [6]. Het beeldvormingsvlak was echter beperkt tot het extreem nabije veld, aangezien de verdwijnende golven exponentieel afnemen, wat wijst op een divergent optisch veld. Deze beperking maakt het onpraktisch voor standaard optische microscopen [7].
De afgelopen jaren zijn verschillende op nanostructuren gebaseerde PL's onderzocht [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Deze PL's kunnen niet alleen de plasmonische focussering in het vlak [8] of in het nabije veld [9] realiseren, maar kunnen ook het focusvermogen bezitten in het verre veld [10,11,12,13], die over het algemeen werden afgebeeld door de scanning optische microscoop [14]. Deze PL's vertoonden echter een grote moeilijkheid om de focussering voorbij de diffractielimiet te realiseren, totdat de dispersierelatie van de metaal-isolator-metaal (MIM) golfgeleider werd gebruikt voor de op nanospleet gebaseerde PL's om de fase op de subgolflengteschaal te moduleren [11] , 15,16,17]. De precieze fasemodulatie draagt bij aan de sub-diffractielimietbrandlijn, en het lineair gepolariseerde licht wordt over het algemeen toegepast als het invallende licht voor deze lenzen. Maar door simpelweg de vergelijkbare ontwerpmethode van eendimensionale nanospleetlenzen in twee dimensies uit te breiden, kan de cirkelvormige focus niet worden gerealiseerd wanneer de rotatiesymmetrische PL werd verlicht door het lineair gepolariseerde licht [18, 19], wat wijst op de sterke polarisatie-afhankelijkheid van de scherpstelprestaties. Bovendien week de brandpuntsafstand ernstig af van de numerieke berekening volgens de golffrontreconstructietheorie, vooral voor de op nanoring gebaseerde PL's [18].
De op nanoring gebaseerde PL's met de rotatiesymmetrie, die voor de eenvoud in de volgende discussie worden genoemd als op nanoring gebaseerde plasmonische lenzen (NRPL's), worden erkend als de vervanging voor de conversielenzen in de subgolflengtefocussystemen. Maar vanuit het perspectief van de excitatie van oppervlakteplasmonpolaritonen (SPP's), is het lineair gepolariseerde licht ongeschikt voor de NRPL's omdat de excitatie-efficiëntie evenredig is met de radiale elektrische veldcomponent van het invallende licht. Ter vergelijking:het radiaal gepolariseerde licht met de cilindrische symmetrie in polarisatie past zich aan aan de structurele eigenschap van NRPL's [25]. Bovendien is dit gepolariseerde licht, gebruikmakend van een ringvormige diafragmastop [26, 27] of Fresnel-zoneplaat [28] in de vorm van een ring, toegepast om de subgolflengte cirkelvormige focus te realiseren. Het radiaal gepolariseerde licht werd dus algemeen toegepast als het invallende licht van NRPL's [20,21,22,23]. Vergeleken met de subgolflengtefocussering met het ruimtelijke filter, bezitten deze PL's het vermogen om de fase van invallend licht in de subgolflengtegolfgeleider te moduleren. De excitatie van oppervlakte-plasmonische (SP) golven kan de transmissie van elektromagnetische golven verbeteren. Het superfocusvermogen van plasmonische lenzen in het verre veld is echter niet aangetoond. Bovendien, hoewel de samengestelde NRPL is voorgesteld om de brandpuntsafstand [24] te moduleren, kon de brandpuntsafstand niet effectief worden gecontroleerd en is de elektrische veldenergie nog steeds geconcentreerd in het midden van het eindoppervlak van de lens.
In dit artikel presenteren we het theoretische ontwerp en de numerieke studie van een NRPL, met de nadruk op de realisatie van superfocusing door gebruik te maken van de polarisatie-eigenschap van invallend licht. We beschrijven het theoretische ontwerp van NRPL's in ons onderzoek en bieden de focusprestaties in het uitvoergebied op basis van de numerieke simulatie van het eindige verschil in tijddomein (FDTD). Om de polarisatie-afhankelijkheid van de focusseringsprestaties te onderzoeken, worden de lineair, circulair, azimutaal en radiaal gepolariseerde lichten allemaal in aanmerking genomen voor verlichting. We bespreken de kenmerken van de elektrische velddistributie in het uitvoergebied, inclusief de sub-diffractie-limietfocussering, de vormen van foci en de modulatie van de brandpuntsafstand, en wijzen op het belang van de coaxiale toestand op de superfocusprestaties.
Methoden
De NRPL's die in dit werk zijn onderzocht, zijn ontworpen met behulp van de golffrontreconstructietheorie die algemeen werd toegepast op de op nanospleet gebaseerde PL's [11, 15]. Om de focus op de gewenste positie te krijgen, wordt de relatieve fasevertraging veroorzaakt wanneer het licht door de i gaat -de individuele nanoring moet voldoen aan de volgende voorwaarde op basis van de geometrische optica:
$$ -\varDelta \phi \left({r}_i\right)=\frac{2\pi \sqrt{f_0^2+{r}_i^2}}{\lambda_0}-\frac{2\pi \sqrt{f_0^2+{r}_1^2}}{\lambda_0}+2 n\pi $$ (1)waar −Δϕ (r ik ) is het relatieve faseverschil tussen de eerste nanoring in het binnenste centrum en de i -de nanoring, r is de straal, λ 0 is de vrije-ruimtegolflengte van het invallende licht, n is een willekeurig geheel getal, en f 0 is de ontworpen brandpuntsafstand.
Het basiselement van de onderzochte NRPL's zijn de nanoringen die in de metaalfilm zijn gevormd. Volgens Ref. [29], wanneer de diameter groter is dan de golflengte van invallend licht, kan de luchtnanoring omringd door metalen wanden worden benaderd met het MIM-golfgeleidermodel, zoals de inzet illustreert in Fig. 1. De fasevertraging wordt voornamelijk bepaald door het reële deel van de voortplantingsconstante β , uitgedrukt als Re(β )•t , waar t is de dikte van de nanoring. Op basis van de dispersierelatie is de complexe voortplantingsconstante β kan worden berekend als:
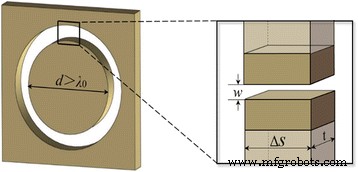
Het MIM-golfgeleidermodel van een individuele nanoring ingebed in de goudfilm. De inzet geeft een vergroot beeld van een willekeurig klein deel van de nanoring
$$ \tanh \left(\frac{w\sqrt{\beta^2-{k}_0^2{\varepsilon}_d}}{2}\right)=-\frac{\varepsilon_d\sqrt{\beta ^2-{k}_0^2{\varepsilon}_m}}{\varepsilon_m\sqrt{\beta^2-{k}_0^2{\varepsilon}_d}} $$ (2)waar k 0 vertegenwoordigt de golfvector in vacuüm en ε d en ε m zijn de permittiviteit van respectievelijk diëlektricum en metaal. Baseer op vgl. (2) kunnen we zien dat de voortplantingsconstante β is afhankelijk van de breedte van een nanoring. Dus voor de platte lens met een gegeven dikte t , wordt de veroorzaakte fasevertraging eenvoudig bepaald door de breedte w van de individuele nanoring wanneer het licht er doorheen gaat. In ons onderzoek is het diëlektricum ingesteld op lucht met de permittiviteit ε d = 1, en de gouden film met een dikte t van 400 nm wordt gebruikt, waarvan de permittiviteit bij de invallende golflengte van 650 nm ε . is m = −12,8915 + 1,2044i [15]. Bovendien, zoals we eerder meldden [16], speelt het koppelingseffect van de propagerende lichten in de twee aangrenzende MIM-golfgeleiders ook een belangrijke rol bij de fasevertraging, vooral wanneer de metalen afstand tussen de wand kleiner is dan tweemaal de huiddiepte δ m , die kan worden geschat met [30]:
$$ {\delta}_m=\frac{1}{k_0}{\left|\frac{\mathrm{Re}\left({\varepsilon}_m\right)+{\varepsilon}_d}{\mathrm{ Re}{\left({\varepsilon}_m\right)}^2}\right|}^{\frac{1}{2}} $$ (3)Dienovereenkomstig is de berekende huiddiepte δ m is ongeveer 28 nm. Door rekening te houden met het koppelingseffect, kan een op nanospleet gebaseerde PL met het superfocusvermogen van 0,38 λ 0 in resolutie werd gerapporteerd in ons eerdere onderzoek [16]. Hier, om de invloed van de polarisatietoestand (SOP) op de scherpstellingsprestaties prominent te analyseren, zijn de afstandswanden tussen twee aangrenzende nanoringen ontworpen om 100 nm te zijn, veel groter dan 2δ m om het koppelingseffect te elimineren.
Het schema van de ontworpen NRPL wordt getoond in Fig. 2, en een totaal aantal van 32 concentrische nanoringen is inbegrepen om het golffront te reconstrueren. De breedte van de nanoring voor de gewenste fasemodulatie varieert van 10 tot 100 nm. De beoogde brandpuntsafstand f 0 is 1300 nm (2 λ 0 ). Om het MIM-golfgeleidermodel efficiënt te gebruiken, is de minimale diameter van de binnenste nanoring ingesteld op 800 nm. Om de brandpuntsverschuiving te vermijden zoals besproken in ons vorige werk [15], is het totale faseverschil zo groot als 10π, met een voorspelde numerieke opening (NA) van 0,96. Als resultaat is de theoretische Rayleigh-diffractielimiet, berekend met 0,61 λ 0 /NA [31], is 413 nm (~0.64 λ 0 ).
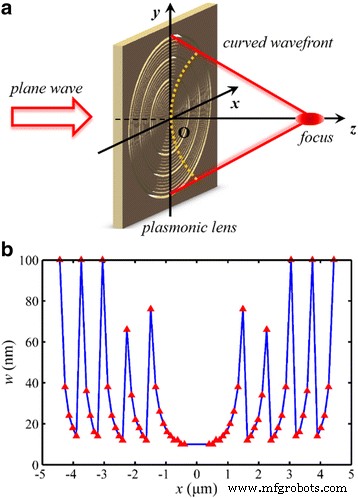
Schema van de NRPL. een Het invallende licht verlicht normaal gesproken de lens. b Structurele parameters van de lens. De coördinaatwaarden van de rode driehoeken vertegenwoordigen de straal r en breedte w van de bijbehorende nanoring
Om de SOP-invloeden van het invallende licht op de ruimtelijke intensiteitsverdelingen te onderzoeken, met name de focusprestaties, werd de ontworpen NRPL verlicht door respectievelijk lineair, circulair, azimutaal en radiaal gepolariseerd licht. Alle gevallen werden berekend door de FDTD numerieke simulaties. Volgens de matrixoptiek kunnen de verschillende gepolariseerde lichten worden beschreven door de Jones-matrixformalismen, en de overeenkomstige matrixuitdrukking werd toegepast om het invallende licht te definiëren. De grens van het model was een perfect op elkaar afgestemde laag (PML) met een laagnummer van 12. Om de rekennauwkeurigheid en het geheugenverbruik in de simulaties in evenwicht te brengen, werd de maaswijdte ingesteld op 10 nm in het uitvoergebied en 5 nm rond de focusgebied.
Resultaten
I lineaire polarisatie
Voor het lineair gepolariseerde licht is de SOP ruimtelijk homogeen, en in dit geval is de richting van de elektrische vector evenwijdig aan de x as. Wanneer het licht de NRPL verlicht, zijn er twee brandpunten die 400 nm van elkaar in het totale elektrische veld verdelen |E | 2 zoals weergegeven in Fig. 3. Hoewel de volledige breedte bij half maximum (FWHM's) van beide 210 nm is (~0,32 λ 0 ) in het brandvlak, geeft het simulatieresultaat aan dat de intensiteitsverdeling blijkbaar verschilt van het ontwerp op basis van de golffrontreconstructietheorie, waarbij er een cirkelvormige focus precies op de z zou moeten zijn as (ook wel de optische as genoemd).
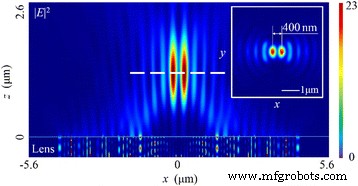
Intensiteitsverdelingspatroon van het totale elektrische veld |E | 2 bij lineair gepolariseerd invallend licht. De inzet toont het intensiteitspatroon in het brandvlak. De brandpuntsafstand is 1215 nm (een afwijking van 6,54%). De FWHM's van beide foci zijn ~0.32 λ 0 , met 400 nm uit elkaar, en de scherptediepte (DOF) is ~1,68 λ 0
Om de verschillen tussen de simulatie en het theoretische ontwerp te analyseren, worden de intensiteitsverdelingen van de elektrische veldcomponenten onderzocht. Zoals weergegeven in Fig. 4, verschijnt er een focus in elliptische vorm en de FWHM in x- en y- richting is 220 nm (~0.34 λ 0 ) en 457 nm (~0,70 λ 0 ), respectievelijk. Dit patroon komt goed overeen met de experimentele resultaten van Ref. [18] waar hetzelfde gepolariseerde licht werd toegepast. De simulatie laat echter zien dat het distributiepatroon van |E | 2 is vergelijkbaar met het patroon van de longitudinale component |E z | 2 die 79,8% van de totale elektrische energie inneemt. Daarom wordt het verschil voornamelijk toegeschreven aan de buitengewone verdeling van |E z | 2 .
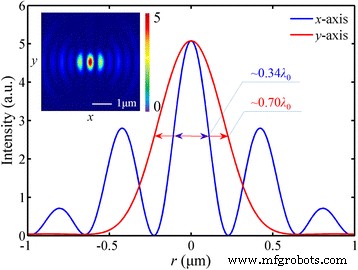
Intensiteitsverdeling van de transversale component |E r | 2 in het brandvlak. De inzet toont de elliptische vorm focus. De brandpuntsafstand is 1425 nm (een afwijking van 9,62%). |E r | 2 neemt 20,2% van de totale elektrische energie in beslag. De DOF is ~1,41 λ 0
Dit fenomeen kan uiteindelijk worden verklaard door de transmissie-eigenschap van de NRPL. Enerzijds hangt de excitatie van SPP's op de grensvlakken van metaal en diëlektricum in het algemeen af van de lokale polarisatierichting van het invallende licht. De transversale elektrische (TE) golven kunnen niet bijdragen aan de excitatie. Aan de andere kant, vanwege de subgolflengtestructuur van de MIM-golfgeleider, kunnen alleen de SP-golven zich door deze lens voortplanten [32]. Met de rotatiesymmetrie van de lens verandert de lokale transversale magnetische (TM) component met de azimuthoek θ in de cosinoïdale vorm. Daarom, zoals getoond in Fig. 5a, is de intensiteitsverdeling van |E | 2 , die zich net boven het eindoppervlak van de lens bevindt, is geconcentreerd in de nabije y = 0 regio (−π/4 < θ < π/4). Dienovereenkomstig planten de Poynting-vectoren zich voort langs de radiale richting op het eindoppervlak, zoals weergegeven in figuur 5b. Dus de vectorrichting van E is in principe evenwijdig aan de optische as, die de hoofdinhoud vormt van E z . Vanwege de symmetrisch constructieve interferentie verschijnen er twee brandpunten in het brandpuntsvlak in plaats van een cirkelvormig brandpunt.
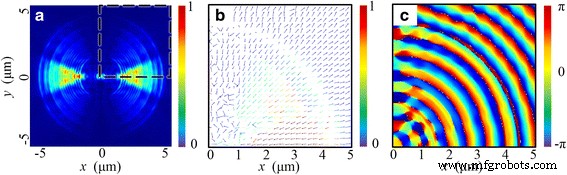
De eigenschappen van de elektrische veldverdeling in de dwarsdoorsnede slechts 50 nm boven het eindoppervlak van de lens. een Genormaliseerde intensiteitsverdeling van |E | 2 . b De Poynting-vectorverdeling binnen de stippellijn regio in a. c De corresponderende faseverdeling van E z
II circulaire polarisatie
Aangezien de toestand van circulair gepolariseerd licht periodiek met de tijd verandert, zijn de gesimuleerde resultaten de tijdgemiddelde veldverdeling. Wanneer de lens wordt verlicht door dit gepolariseerde licht, ontstaat er een ringvormige focus in |E z | 2 . Zoals getoond in Fig. 6a, is de brandpuntsafstand in dit veld 1185 nm, wat een afwijking van 8,85% ten opzichte van de ontworpen waarde laat zien. De breedte van de donut is 210 nm (~0.32 λ 0 ), en de straal is 400 nm. De scherptediepte (DOF) is ~1,65 λ 0 . Het gewicht van |E z | 2 is 80,6% van de totale elektrische energie. Bovendien, in |E r | 2 , genereert de superpositie in het ruimtelijke domein een cirkelvormige focus met de brandpuntsafstand van 1405 nm (een afwijking van 8,08%). De FWHM is 295 nm (~0,45 λ 0 ) in dit veld, en de DOF is ~1,68 λ 0 . Verder zijn beide distributiepatronen in r-z vlak lijken op die in de x -z vlak bij lineair gepolariseerd invallend licht. Door rekening te houden met de radiale elektrische veldcomponent, kan de FWHM worden teruggebracht tot 222 nm (~0.34 λ 0 ).
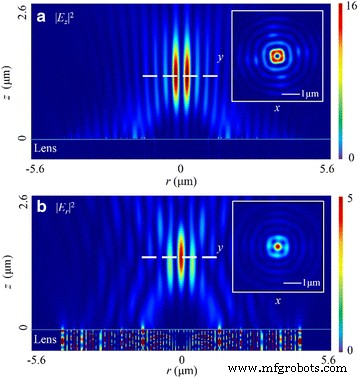
Intensiteitsverdelingspatronen van |E z | 2 en |E r | 2 in r-z vlak bij circulair gepolariseerd licht. een In |E z | 2 , de FWHM, DOF en brandpuntsafstand is ~0.32 λ 0 , ~1.65 λ 0 , en 1185 nm, respectievelijk. b In |E r | 2 , de FWHM, DOF en brandpuntsafstand is ~0,45 λ 0 , ~1,68 λ 0 , en 1405 nm, respectievelijk
III Azimutale polarisatie
Voor het azimutaal gepolariseerde invallende licht staan de elektrische vectoren loodrecht op de radiale richting, die evenwijdig zijn aan het goud/vacuüm-interface van de NRPL. Omdat het azimutaal gepolariseerde licht de lens verlicht, slagen de lokale TE-golven er niet in om de SPP's op de interface te prikkelen. De transmissieafstand in nanoringen is dus evenredig met hun breedtes zoals weergegeven in figuur 7. Aangezien zowel de structuur als de verlichting rotatiesymmetrisch zijn, worden slechts de helft van het intensiteitsverdelingspatroon en de structuur van de NRPL getoond. Het doorgelaten licht kan worden verwaarloosd en er is geen duidelijke focus in het uitvoergebied.
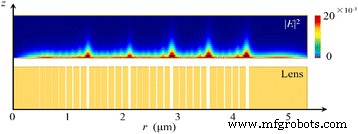
Intensiteitsverdelingspatroon in het lensgebied en zijn dwarsdoorsnede. De transmissieafstand van de niet-SP-golven in nanoringen is evenredig met de spleetbreedte
IV radiale polarisatie
In overeenstemming met het azimutaal gepolariseerde licht, kan het radiaal gepolariseerde licht worden beschouwd als de lokale TM-golf, en deze polarisatie-eigenschap past bij de excitatieconditie van SPP's, wat bijdraagt aan een hogere maximale intensiteit in de focus. In totaal elektrisch veld E , de maximale intensiteit is vijf keer groter dan die voor het lineair gepolariseerde invallende licht. Bovendien is er een cirkelvormige focus met de 276-nm (~0.42 λ 0 ) FWHM in |E | 2 , zoals weergegeven in Fig. 8. De gesimuleerde intensiteitsverdeling lijkt veel op het focusvermogen van de lens met hoge NA-breking [33]. Bovendien is deze scherpstelprestatie nog steeds afhankelijk van |E z | 2 , die 82,0% van de totale elektrische energie inneemt.
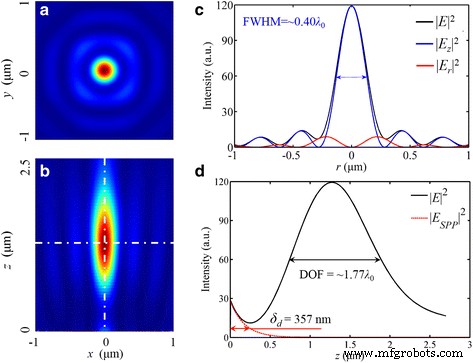
Intensiteitsverdeling van |E | 2 bij radiaal gepolariseerd invallend licht. een , b De verdeling in het brandvlak en die in x -z dwarsdoorsnede. c Het intensiteitsprofiel in radiale richting. d Het intensiteitsprofiel langs de optische as waar de zwarte ononderbroken lijn is de totale verdeling van de elektrische veldintensiteit in simulatie en de rode stippellijn is de berekende curve van SPP. De brandpuntsafstand is 1275 nm (een afwijking van 1,92%). De FWHM van |E | 2 en |E z | 2 is 272 nm (~0,42 λ 0 ) en 260 nm (~0.40 λ 0 ), respectievelijk. De DOF is ~1,77 λ 0
Anders dan in de vorige gevallen, is er een cirkelvormige focus in |E z | 2 . Bovendien bepaalt deze component ook het distributiepatroon in |E | 2 . Zoals weergegeven in Fig. 9a, is de FWHM in |E z | 2 is 260 nm (~0.40 λ 0 ) die dicht bij die van de brandlijn ligt in het geval van op nanospleet gebaseerde PL [16]. In het bijzonder is de brandpuntsafstand 1275 nm. Ten opzichte van de ontworpen waarde neemt de relatieve fout af tot 1,9%. De brandpuntsafstand is echter 1455 nm (een afwijking van 11,2%) in |E r | 2 . Zoals weergegeven in Fig. 9b, is er een focus in de vorm van een donut met een breedte van 227 nm (~0,35 λ 0 ) in dit veld. De DOF is ~ 1.60 λ 0 .
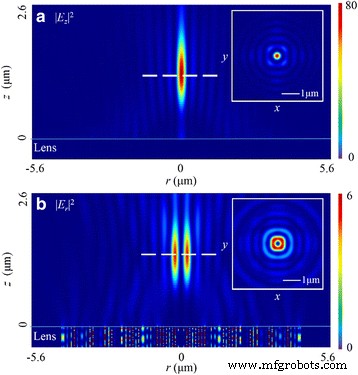
Intensiteitsverdelingspatronen van |E z | 2 en |E r | 2 in r-z vlak bij radiaal gepolariseerd licht. een |E z | 2 patroon in de r-z vlak. De inzet toont een cirkelvormige focus in het brandvlak. b De transversale |E r | 2 patroon in de r-z vlak. De inzet toont een ringvormige focus in het brandvlak
De fasevertraging van de SP-golven in nanoringen wordt onderzocht, zoals weergegeven in Fig. 10. De simulatie geeft aan dat de fasemodulatie dramatisch wordt beïnvloed door de structurele parameters van de NRPL en de gesimuleerde fasevertragingen tussen het invallende oppervlak en het uitgangsoppervlak zijn in principe identiek aan de berekende waarden op basis van Vgl. (2). Op het eindoppervlak van de lens planten de SP-golven zich nog steeds voort langs de radiale richting en er is een hotspot in het midden van het oppervlak, waarvan de intensiteit een vijfde van de focusintensiteit is. De constructieve interferentie van de SP-golven, met de rotatiesymmetrische verdeling, construeert de voortplantende golven en realiseert de cirkelvormige focus in het quasi-verre veld.
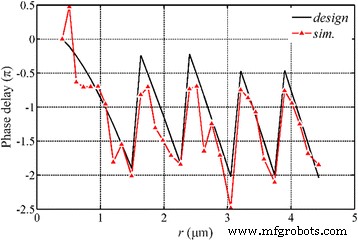
Faseanalyse van de NRPL onder het radiaal gepolariseerde invallende licht
Discussies
I Superfocusing-vermogen van NRPL's
Omdat de invallende lichten met verschillende SOP's worden toegepast, inclusief de lineaire, circulaire en radiale polarisaties, kunnen de sub-diffractie-limietfoci worden gerealiseerd. Hoewel de focusvorm wordt beïnvloed door de SOP, overwinnen de karakteristieke afmetingen van deze foci allemaal de Rayleigh-diffractielimiet (413 nm). De simulatieresultaten demonstreren met succes het superfocusvermogen van de NRPL, en de intensiteitsverdeling in het brandpuntsvlak is vergelijkbaar met de Bessel-functie die wordt gebruikt om de niet-diffractiebundel te beschrijven.
Voor het geval van het radiaal gepolariseerde invallende licht, als voorbeeld getoond in Fig. 11, de intensiteitsverdeling in |E z | 2 is identiek aan de nulde orde Bessel-functie J 0 (K spp ⋅ n ⋅ r ), waar n en r is respectievelijk de brekingsindex van het omgevingsmedium en de radiale afstand tot de optische as. De FWHM van de focus is iets groter dan de grootte van de hoofdlob berekend met J 0 . In het bijzonder geven de simulaties aan dat de niet-diffractiebundel kan worden gerealiseerd in het quasi-verre veld. De SP-golven, als een soort verdwijnende golf, nemen exponentieel af wanneer ze zich vanaf het uitgangsoppervlak voortplanten, en de voortplantingsafstand in het vacuüm kan worden berekend met [30]:
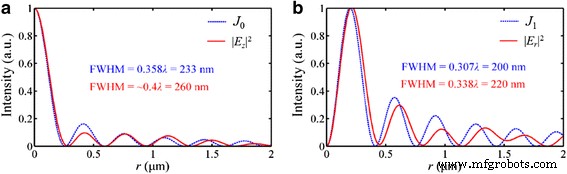
Intensiteitsprofielen van de NRPL in het brandvlak onder het radiaal gepolariseerde invallende licht. een De verdeling van |E z | 2 lijkt op de nulde orde Bessel-functie J 0 . b De verdeling van |E r | 2 lijkt op de eerste-orde Bessel-functie J 1
$$ {\delta}_d=\frac{1}{k_0}{\left|\frac{\mathrm{Re}\left({\varepsilon}_m\right)+{\varepsilon}_d}{{\varepsilon_d }^2}\right|}^{\frac{1}{2}} $$ (4)waar ε d en ε m zijn de permittiviteit van respectievelijk diëlektricum en metaal. Dus, δ d is 357 nm wat consistent is met de simulatie zoals getoond in Fig. 8d. Daarom kan de intensiteit van de SP-golven in de focus worden verwaarloosd in het quasi-far-field-gebied.
II Vorm van focus
Door de SOP te moduleren, kunnen de elliptische, cirkelvormige en donutvormige brandpunten worden gerealiseerd in het brandpuntsvlak, zoals weergegeven in Fig. 12. Het fenomeen wordt toegeschreven aan de brandpuntsafstand onder de golflengte, en we kunnen het cirkelvormige type niet realiseren focus in zowel elektrische als magnetische velden tegelijkertijd. Zo wordt een focus van het donuttype gerealiseerd in de magnetische (of elektrische) velden, terwijl een focus van het cirkelvormige type wordt bereikt in het overeenkomstige elektrische (of magnetische) veld. Vooral omdat er geen longitudinaal magnetisch veld is, is de intensiteitsverdeling van |H | 2 is hetzelfde als het patroon van |E r | 2 . Bovendien, |E z | 2 neemt ongeveer 80,0% van de totale elektrische energie in beslag en de schaal wordt niet beïnvloed door de SOP's van het invallende licht.
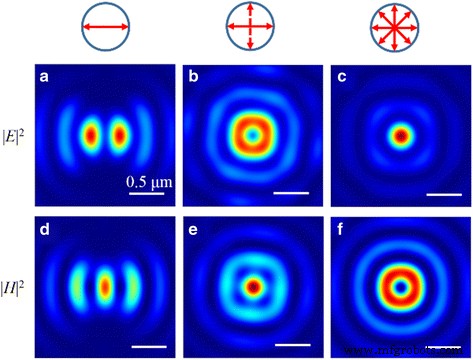
De genormaliseerde intensiteitspatronen van het elektrische veld |E | 2 en magnetisch veld |H | 2 in het brandvlak wanneer de NRPL wordt verlicht door het gepolariseerde licht. een |E | 2 en d |H | 2 verdeling met lineair gepolariseerd invallend licht. b |E | 2 en e |H | 2 distributie met circulair gepolariseerd invallend licht. c |E | 2 en f |H | 2 verdeling met radiaal gepolariseerd invallend licht
III modulatie van brandpuntsafstand
De gesimuleerde brandpuntsafstand ligt in verschillende gevallen in principe dicht bij de gewenste positie f 0 (1300 nm), zoals weergegeven in Tabel 1. Maar we realiseren ons dat de brandpuntsafstand in het transversale veld |E r | 2 is ongeveer 200 nm langer dan die in het longitudinale veld |E z | 2 , ongeacht de SOP van het invallende licht en de afwijking die gewoonlijk bestaat.
In theorie is de golffrontreconstructietheorie geschikt voor het ontwerpen van de NRPL met een willekeurige brandpuntsafstand van het nabije veld naar het verre veldgebied. Of de werkelijke brandpuntsafstand van een ontworpen plasmonische lens echter goed overeenkomt met de ontworpen brandpuntsafstand, hangt af van het totale faseverschil van de lens. De afwijking kan worden toegeschreven aan het onderscheid tussen de focus van het amplitudetype en de focus van het fasetype [34]. Omdat de fasemodulatie in de MIM-golfgeleider gericht is op de radiale component, is de brandpuntsafstand in |E r | 2 kan worden gemoduleerd door de golffrontreconstructietheorie, wanneer aan het totale faseverschil van ten minste 2π wordt voldaan [15]. Voor de longitudinale component is een groter totaal faseverschil (>10π) gunstig voor de consistentie. Zoals getoond in Fig. 13, wanneer het faseverschil toeneemt van 2π tot 16π, dienovereenkomstig de NA van 0,75 tot 0,96, de amplitude-type focus in |E z | 2 beweegt van het uitgangsoppervlak van de lens naar de gewenste positie. Als de intensiteitsverdeling van |E | 2 wordt bepaald door |E z | 2 kan de NA de brandpuntsafstand in het totale elektrische veld dramatisch beïnvloeden. De verandering van de brandpuntsafstand in |E z | 2 neemt geleidelijk af, samen met de toename van het totale faseverschil. Aan de andere kant is de positie van het fasetype focus in |E r | 2 relatief stabiel is. Wanneer de NRPL met een hoge NA wordt toegepast, is er toch een afwijking in brandpuntsafstand afgeleid op basis van de intensiteitsverdeling van |E x | 2 en |E z | 2 , en de afwijking blijft bijna onveranderlijk. Daarom kan de brandpuntsafstand van de NRPL's effectief worden gecontroleerd door de fasemodulatie en structurele optimalisatie, hoewel dezelfde brandpuntsafstand niet kan worden bereikt in de transversale en longitudinale componentvelden.
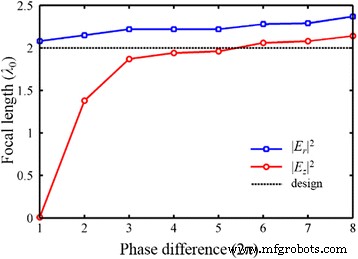
The focal length of the NRPL with the increase of total phase difference from 2π to 16π
IV Focusing Performace in the Non-Coaxial Situation
The non-coaxial situation is a common problem in the experiment, and its effect on the focusing performance should be considered. As shown in Fig. 14, the center of the radially polarized light deviates 3 μm from the optical axis of the NRPL along the x axis. Compared with Figs. 8 and 9, the intensity distributions both in x-z cross section and in focal plane are apparently changed. In the longitudinal electric field, an elliptical focus is located at 1340 nm away from the exit surface of the lens. The FWHMs in x-z and y-z planes are 0.51 and 0.38 λ 0 , respectievelijk. On the other hand, the distribution in transverse field is also distorted, where the intensity of one side lobe is higher than the other one. Furthermore, compared with the coaxial condition, the decrease of the maximum intensity in the total electric field is more than 85%.
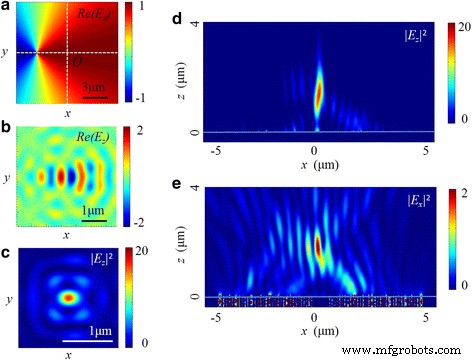
The intensity distribution of the NRPL in the non-coaxial situation. een The real part of E x of radially polarized incident light. b , c The distribution of Re(E z ) and |E z | 2 in the focal plane. d , e The distribution of |E z | 2 and |E x | 2 in the x-z plane
The preliminary simulation indicates that the non-coaxial situation indeed influences the intensity distribution and the desired focusing performance of lens. Therefore, it is essential to guarantee the coaxiality between the incident light and the lens center during the experiment.
Conclusions
In summary, we build a NRPL with a high NA utilizing the wavefront reconstruction theory and the dispersion relation of the MIM waveguide. We also investigate the polarization-dependent focusing performance in the quasi-far field, including the focal length, FWHM, DOF, and the maximum intensity. The conventional polarized light, such as the linearly, circularly, radially, and azimuthally polarized light, are all considered. The simulations demonstrate the superfocusing capability of the designed NRPL. Utilizing the polarization-dependent property, the sub-diffraction-limit elliptical-, circular-, and donut-shape foci can be realized. However, one limitation of this work is that the proposed design strategy to realize the superfocusing performance of NRPLs is aimed for the quasi-far-field region, although to the best of our knowledge, the similar focusing capability in this region is rarely reported. In addition, we discover the underlying physical phenomenon on the focal shift and propose a more effective way to control the focusing position by employing both the transverse and longitudinal fields. There are considerable engineering applications for the nanoring-based superfocusing lenses, ranging from the super-resolution imaging, particle acceleration, quantum optical information processing to the optical data storage.
Afkortingen
- DOF:
-
Depth of focus
- FDTD:
-
Finite-difference time-domain
- FWHM:
-
Full-width at half maximum
- MIM:
-
Metal-insulator-metal
- NRPL:
-
Nanoring-based plasmonic lenses
- PML:
-
Perfectly matched layer
- SOP:
-
State of polarization
- SPPs:
-
Surface plasmon polaritons
- TE:
-
Transverse electric
- TM:
-
Transverse magnetic
Nanomaterialen



