Plasmonresonantie bij fotoabsorptie van colloïdale sterk gedoteerde ZnO-nanokristallen

Achtergrond

De optische eigenschappen van nanodeeltjes worden voor een groot deel bepaald door de aanwezigheid van gelokaliseerde oppervlakteplasmonresonanties (LSPR) in hun excitatiespectra [1-8]. Kriegel et al. [2] publiceerde een vrij gedetailleerd overzicht van opkomende colloïdale nanokristallen (NC's), waaronder met onzuiverheden gedoteerde metaaloxide-NC's, koperchalcogenide-NC's en gedegenereerd gedoteerde halfgeleider-NC's, en besprak uitgebreid hun optische eigenschappen en toepassingen voor sensing, near-field verbetering van spectroscopie, afstembare opto-elektronische apparaten of biomedische toepassingen. Al deze nieuwe materialen zijn een alternatief voor NC's van edelmetalen die de afgelopen decennia uitgebreid zijn bestudeerd; voor een uitgebreid overzicht, zie ook Ref. [9]. Het is aangetoond dat het mogelijk is om de optische respons van zwaar gedoteerde halfgeleider nanokristallen (NC's) af te stemmen op het IR-bereik [10-15], door in te werken op verschillende controleparameters [11, 13, 16-20], waardoor nieuwe perspectieven voor nanofotonica. Het belangrijkste voordeel van halfgeleider-NC's is dat de draaggolfdichtheid over een breed interval kan worden afgestemd. Terwijl een metalen geleider een vaste elektronendichtheid heeft, kan een halfgeleider worden gedoteerd om willekeurige dragerdichtheden te bereiken in een bereik van 10 ¹⁶ ÷10 ²² cm ⁻³ [10, 13, 21, 22]. Dragerdoping geeft toegang tot afstembare LSPR in een breed frequentiebereik van de THz tot IR en het zichtbare gebied [13]. Een dergelijke afstembaarheid van de draaggolfdichtheid is een unieke eigenschap van halfgeleidernanodeeltjes en kan niet worden bereikt met metalen druppeltjes [23-25]. Doping kan worden gedaan door verschillende soorten onzuiverheden in het kristalrooster op te nemen [7, 10, 18], en de plasmonresonantiefrequentie kan worden afgestemd of geschakeld door actieve controle van dragers [13, 16-18, 21, 22]. Bovendien hangen de plasmonfrequentie en de lijnvorm niet alleen af ​​van de dragerdichtheid van de NC, maar ook van het type doping, dat "bulkachtig" of "oppervlakteachtig" kan zijn [15, 22]. In het eerste geval wordt de lading van vrije dragers geneutraliseerd door de lading van dopingonzuiverheden over het hele NC-volume, terwijl in het laatste geval de vrije dragers in het NC-volume worden geïnjecteerd door donoren/acceptors van de omringende media die zich aan de NC-interface.

Theoretische studies van de optische respons van halfgeleider nanodeeltjes hebben significante verschillen aangetoond tussen kwantummechanische en klassieke beschrijvingen [5, 22, 24, 26]. Naarmate de nanodeeltjes kleiner worden, verschuift de plasmonresonantie naar hogere energieën met zichtbare afwijking van klassieke voorspellingen [5, 21, 22]. Bovendien ondergaan de dynamische eigenschappen van sterk gedoteerde NC's een overgang van het groottekwantisatieregime naar het klassieke regime van plasmonoscillaties [22]. Het kan worden waargenomen door het aantal dragers of de NC-grootte te variëren.

In dit werk presenteren we een theoretische analyse van de optische respons van gefotodopeerde ZnO NC's zoals experimenteel onderzocht in Ref. [21, 27]. In deze experimentele studies werden de fotoabsorptiedwarsdoorsneden van colloïdaal ZnO NC met vaste afmetingen en dragerdichtheden gemeten. De foto-elektronen van de geleidingsband werden gegenereerd in ZnO NC door middel van fotodoping, terwijl de gaten werden opgesloten door de gatenvangende centra in omringend tolueen. De gemiddelde geleidende elektronenconcentratie n _e in bijna bolvormige fotogedoteerde nanokristallen met verschillende stralen (van 1,75 tot 6 nm) bleek een bovengrens van (1,4±0,4)×10 ²⁰ te worden bereikt cm ⁻³ [21, 27]. De intraband-absorptie werd gemeten in het bereik van 0,2 tot 1,0 eV en er werden significante verschillen waargenomen met de klassieke voorspelling van het Drude-model. De auteurs toonden aan dat een kwantummechanische benadering gebaseerd op overgangen van één deeltje de experimentele grootte-afhankelijkheid van de resonantiefrequentie alleen kwalitatief opleverde [21].

Het doel van dit artikel is om de theoretische benadering van plasmonresonanties in gefotodoteerde ZnO NC's opnieuw te bekijken door verder te gaan dan de niet-interagerende benadering van één deeltje [21, 27]. Het is gebaseerd op de zelfconsistente kwantummechanische behandeling van geleidingselektronen met veel lichamen binnen de random phase approximation (RPA) met lokale uitwisseling [28]. Er werd aangetoond dat vrije ladingsdragers in halfgeleider nanodeeltjes atomaire schillen vormen [29, 30]. We lossen de lokale dichtheidsbenadering (LDA) Kohn-Sham-vergelijkingen op om de elektronenschilstructuur te beschrijven. Binnen de RPA wordt rekening gehouden met de elektronencorrelaties die verantwoordelijk zijn voor de collectieve plasmonexcitaties. We laten zien dat de plasmonresonantie in ZnO NC aanzienlijk verschilt van de bekende Mie-resonantie in metalen druppeltjes. In tegenstelling tot bulkachtige gedoteerde NC's, is er geen herstellende positieve lading in oppervlakteachtige gedoteerde ZnO NC. Bijgevolg duwt de Coulomb-afstoting tussen vrije elektronen ze dicht bij het NC-oppervlak. Deze specifieke elektronische configuratie leidt op zijn beurt tot een dipoolmodus, waarbij alleen de hoekgraden van vrijheid worden geëxciteerd, terwijl de elektronische radiale beweging niet is betrokken. In tegenstelling tot het gewone Mie-oppervlakte-dipoolplasmon, waar elektronen pure translatie-oscillaties ondergaan, ondergaan elektronen in sterk gedoteerde ZnO NC's tangentiële trillingen in de vrij dunne elektronische schil op een manier die vergelijkbaar is met de plasmon-oscillaties in fullereen-moleculen [31]. We laten ook zien dat de overgang van deze plasmonmodus van het klassieke naar kwantumopsluitingsregime wordt bepaald door de verhouding van de NC-grootte tot de effectieve Bohr-straal en niet afhankelijk is van het aantal vrije elektronen. De kwantumeffecten in plasmonoscillaties resulteren in een blauwe verschuiving van de dipoolresonantiefrequentie die mooi overeenkomt met de experimenteel waargenomen LSPR-grootteafhankelijkheid [21].

Methoden

Het doel van de studie is de theoretische analyse van optische eigenschappen van gefotodoteerde ZnO-nanokristallen. De configuraties van de grondtoestand van de systemen met variërende aantallen deeltjes werden berekend binnen de lokale dichtheidsbenadering. De golffuncties van de grondtoestand zijn energieën van één deeltje die werden verkregen door zelfconsistente numerieke oplossing van de reeks Kohn-Sham-vergelijkingen [32]. De volledige basis van de toestanden van één deeltje werd gegenereerd met behulp van de B-spline-methode [33] door de basisfuncties uit te breiden in een holte met een grote straal over een eindig aantal B-splines. De straal van de spouw werd gelijk gekozen aan de NC-straal. De gewenste nauwkeurigheid van de berekeningen met het gebruik van de B-spline discrete basis werd bereikt door de juiste keuze van het aantal en de volgorde van de B-splines die in de berekening werden gebruikt. We hebben 50 B-splines van de orde 7 gebruikt om voldoende nauwkeurigheid te bereiken (10 ⁻⁵ ) van de resultaten. De standaard subroutine RG uit het eigensysteem-subroutinepakket (EISPACK) is gebruikt voor het verkrijgen van de eigenwaarden en de eigenvectoren van de RPA-matrixvergelijking [28], welke oplossing ons de set van dipool-excitatie-energieën en bijbehorende oscillatorsterkten verschaft. Het fotoabsorptiespectrum is verkregen door de verbreding van de berekende oscillatiesterkteverdeling door Lorentz-profielen met de vaste vouwbreedte.

Resultaten en discussie

Grondstaatstructuur

We beschouwen het systeem van N geleidingsbandelektronen gelokaliseerd binnen de ZnO NC met straal R . Na [21] nemen we aan dat het aantal elektronen varieert met de NC-grootte als N =4π n _e R ³ /3, waarbij de vaste gemiddelde elektronenconcentratie, n _e =1.4×10 ²⁰ cm ⁻³ , wordt bepaald door het hoogst haalbare niveau in het fotodopingproces. De straal van de beschouwde NC's varieert van 2,4 tot 6 nm; dienovereenkomstig, het aantal geleidingselektronen, N , variëren van 8 tot 128.

We gebruiken de benadering van de envelopfunctie om de elektronenbeweging te beschrijven, ervan uitgaande dat R veel groter is dan de roosterconstante. Het is bekend dat de elektronische bandstructuur van bulk ZnO wordt gekenmerkt door een niet-isotroop en niet-parabolisch energiespectrum [34]. Voor het huidige probleem van de collectieve dynamiek van N gedelokaliseerde elektronen, zullen we deze kleine effecten van het energiespectrum verwaarlozen en een isotrope parabolische energiedispersie beschouwen met effectieve massa \(m_{e}^{*}=0.3~m_{e}\) [34]. Om dezelfde reden beschouwen we de ZnO NC's als bolvormige systemen.

Omdat de elektronen sterk gelokaliseerd zijn binnen het ZnO NC-volume vanwege de hoge geleidingsbandoffset aan de NC-interface [6], dwingen we alle elektronengolffuncties te verdwijnen aan de NC-grens r =R . Dus beschouwen we N interagerende elektronen gelokaliseerd in een oneindige bolvormige put waarvan de algehele ladingsneutraliteit wordt verzekerd door een positieve verdeling van het ladingsoppervlak die geen enkel veld binnen de NC creëert. De effectieve Hamiltoniaan van het beschouwde systeem is eenvoudig:

$$ \hat{H} =\sum\limits_{a} \frac{\hat{\mathbf{p}}^{2}_{a}}{2 m_{e}^{*}}+ \frac {1}{2}\sum\limits_{a,b}V\left(\mathbf{r}_{a},\mathbf{r}_{b} \right), $$ (1)

waar V (r _een ,r _b ) staat voor het paar-elektron Coulomb-interactie. De expliciete uitdrukking ervan, rekening houdend met de polarisatie van ZnO-materiaal en de omringende media, wordt geschreven als een multipooluitbreiding [3],

$$ \begin{aligned} &V\left(\mathbf{r}_{a},\mathbf{r}_{b} \right) =\sum\limits_{L,M} \frac{4\pi V_ {L}}{2L+1} Y_{LM}(\mathbf{n}_{a})Y^{*}_{LM}(\mathbf{n}_{b}), \\ &V_{L } =\frac{e^{2}}{\varepsilon_{i}}\left(\frac{r^{L}_<}{ r^{L+1}_>}+ \frac{\left( \varepsilon_{i}-\varepsilon_{m}\right)\left(L+1\right)\left(r_{a} r_{b}\right)^{L}}{\left(L\varepsilon_{ i}+(L+1)\varepsilon_{m}\right) R^{2L+1}} \right), \end{aligned} $$ (2)

waar r _< en r _> zijn respectievelijk de kleinste en grootste van de twee radiale posities. Aan de diëlektrische constanten van ZnO en tolueen wordt hun bulkwaarde toegekend ε _ik =3.7 en ε _m =2,25 [21], respectievelijk. Met deze parameters is de effectieve Bohr-straal \(a_{0}=\hbar ^{2} \varepsilon _{i}/m_{e}^{*} e^{2} =0,65\) nm kleiner dan de NC-straal.

De elektronenenergieën van één deeltje, ε _ik , en envelopgolffuncties ψ _ik voldoen aan de reeks LDA Kohn-Sham-vergelijkingen,

$$ \left[\frac {\hat{\mathbf{p}}^{2}}{2 m_{e}^{*}}+ V_{mf}(\mathbf{r})\right]~ \ psi_{i}(\mathbf{r}) =\epsilon_{i} \psi_{i}(\mathbf{r}), $$ (3)

waarbij de gemiddelde veldpotentiaal V _mf wordt gegeven door de som van direct, V _D (r ), en ruil, V _x (r ), onderdelen,

$$ \begin{aligned} &V_{mf}(\mathbf{r}) =V_{D}(\mathbf{r}) +V_{x}(\mathbf{r}), \\ &V_{D}( \mathbf{r}) =\int V(\mathbf{r},\mathbf{r}^{\prime})\rho(\mathbf{r}^{\prime})d\mathbf{r}^{ \prime}, \quad V_{x}(\mathbf{r}) =-\frac{e^{2}}{\varepsilon_{i}}\left(\frac{3\rho(\mathbf{r} )}{\pi}\right)^{1/3}, \end{uitgelijnd} $$ (4)

waarbij \(\rho =\sum _{i} |\psi _{i}|^{2}\) de elektronendichtheid is. Merk op dat we de lokale dichtheidsafhankelijke uitwisselingsterm in zijn Dirac-vorm kunnen vervangen door een meer realistische lokale dichtheidsafhankelijke uitwisselingscorrelatieterm, zoals gewoonlijk wordt gedaan. We doen het niet omdat de theoretische constructie van aangeslagen toestanden die automatisch zal volgen een groot deel van de grondtoestandcorrelaties van RPA-aard verklaart.

Voor de eenvoud beschouwen we sferisch symmetrische elektronenconfiguraties met gesloten elektronische schillen. In dit geval worden de golffuncties van één deeltje gegeven als de producten van radiale, hoekige en spincomponenten [35]. Bijgevolg is de index i =(n ,ik ), waar n is het radiale kwantumgetal en l het impulsmoment. De numerieke oplossing van Vgl. (3) voor elektronengetal N <130 toonde aan dat de elektronenconfiguratie van de grondtoestand was gemaakt van bezette elektronische toestanden met de laagste radiale kwantumgetallen n =1. Deze elektronische toestanden hebben knooppuntloze radiale golffuncties en verschillen door de waarden van hoekmoment l . Dus, rekening houdend met de spindegeneratie, zijn de "magische" aantallen elektronen voor dergelijke symmetrische configuraties N =2(l _max +1) ² , waar l _max is het maximale impulsmoment van de hoogst bezette elektronische toestand. In Fig. 1 tonen we de dichtheidsverdelingen ρ (r ) voor de NC met N =18, 50, 128 elektronen. Men kan zien dat de radiale dichtheidsverdeling steeds smaller wordt en naar het NC-interface verschuift naarmate de grootte groter wordt. Het inzetstuk van Fig. 1 toont de grootte-afhankelijkheid van de gemiddelde elektronische waarde van de elektronische radiale verdeling 〈r 〉 op de NC-straal R en de verhouding δ r /R , van zijn verspreiding \(\delta r =\sqrt {\langle r^{2} \rangle - {\langle r\rangle }^{2}}\) (die kan worden beschouwd als de effectieve breedte van de elektronische schaal) naar de NC-straal. Deze verhouding die slechts ∼ 0,15 bedraagt ​​voor de kleinste NC met N =8 elektronen nemen snel af voor de grotere systemen. Numeriek, de breedte van de elektronische schaal δ r is ongeveer twee derde van de effectieve Bohr-straal a ₀ terwijl de piek van de elektronische schaal wordt verschoven van de NC-interface vanwege de kwantumreflectie met ongeveer R −〈r 〉≃2a ₀ . Dit kenmerk van het elektronische systeem volgt uit de sterke Coulomb-afstoting die de elektronen naar de NC-grens duwt en een holle bolvormige ladingsverdeling vormt. Als de NC-straal groot genoeg is, zal de Coulomb-afstotingskracht bij de NC-grens e ² N /ε _ik R ² wordt veel sterker dan de middelpuntvliedende kracht \(\hbar ^{2}l(l+1)/m_{e}^{*}{\langle r \rangle }^{3}\) zelfs voor de hoogste bezette toestand met \(l=l_{max}=\sqrt {N/2}-1\). Men kan zien dat hun verhouding a . bedraagt ₀ /2R . Dat is de reden waarom de radiale en hoekige elektronenbewegingen scheiden als R ≫een ₀ . In dit geval is het elektronische systeem vergelijkbaar met een kwantumrotator, bijvoorbeeld het energiespectrum van bezette toestanden van één deeltje ε _ik van Verg. (3) wordt goed benaderd door de formule,

$$ \epsilon_{1,l} - \epsilon_{1,0} =\frac{\hbar^{2}l(l+1)}{2m_{e}^{*} {\langle r\rangle} ^{2}}. $$ (5)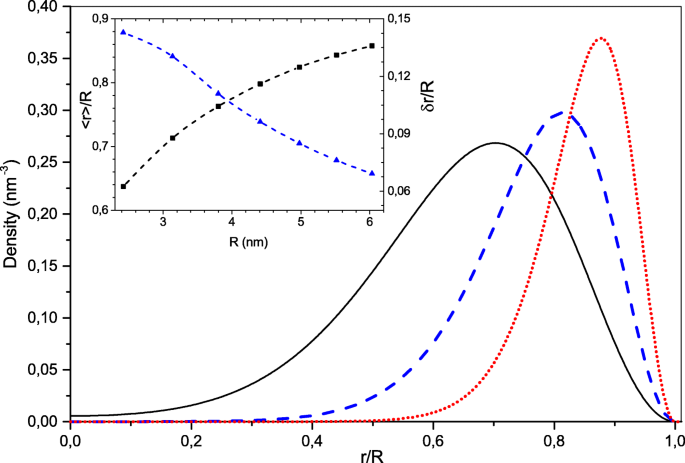

Radiale dichtheidsverdelingen voor NC's met verschillende aantallen gedelokaliseerde elektronen, N =18 (effen zwart zoals), 50 (blauwe stippellijn), 128 (rode stippellijn). In de inzet wordt de gereduceerde gemiddelde straal (zwart) en de spreiding (blauw) weergegeven als een functie van de NC-straal

Optische respons

In de lineaire responsbenadering induceert een extern harmonisch elektrisch veld tijdsafhankelijke zelfconsistente velden van dezelfde frequentie. De kennis van de bijbehorende trillingen met kleine amplitude geeft informatie over de aangeslagen toestanden van de dipool en over de overgangswaarschijnlijkheden tussen grondtoestand en aangeslagen toestanden. Voor een systeem waarvan de grondtoestand een Slater-determinant is |Φ ₀>, de gecorreleerde veel-lichaams-dipool-aangeslagen toestanden binnen de RPA-benadering zijn geconstrueerd als een lineaire superpositie van een deeltje-gat-excitatie [36]:

$$ |\Phi_{\nu}>=\sum_{i>F,j. $$ (6)

De indexen i ,m , (j ,n ) verwijzen naar de toestanden van één deeltje boven (onder) het Fermi-niveau F; \(\hat {a}^{+}\) en \(\hat {a}\) zijn respectievelijk de operators voor het maken en vernietigen van één deeltje.

De voorwaartse, \(X_{ij}^{\nu }\), en de achterwaartse, \(Y_{ij}^{\nu }\), amplitudes kunnen worden verkregen door het oplossen van de matrix RPA-vergelijking [ 28]:

$$ \left(\begin{array}{ll} \mathbf{A} &\mathbf{B} \\ \mathbf{B}^{\star} &\mathbf{A}^{\star} \end{ array} \right) \left(\begin{array}{l} \mathbf{X}^{\nu} \\ \mathbf{Y}^{\nu} \end{array} \right) =\omega_{ \nu} \left(\begin{array}{l} \mathbf{X}^{\nu} \\ -\mathbf{Y}^{\nu} \end{array} \right), $$ (7 )

waarbij de eigenwaarden ω _ν zijn de excitatie-energieën. De matrices A en B worden als volgt gedefinieerd

$$ {\begin{aligned} A_{ij,mn}&\,=\,\delta_{im}\delta_{jn}\left(\varepsilon_{i}-\varepsilon_{j}\right) \,+ \, \links\langle in\links| \hat{v}\rechts| jm\right\rangle, \quad B_{ij,mn}&\,=\,\left\langle im\left| \hat{v}\rechts| jn\right\rangle \\ \hat{v}(\mathbf{r},\mathbf{r}^{\prime}) &=V(\mathbf{r},\mathbf{r}^{\prime} )+ \delta\left(\mathbf{r}- \mathbf{r}^{\prime}\right)\delta V_{x}/\delta \rho. \end{uitgelijnd}} $$ (8)

Merk terloops op dat de achterwaartse amplituden, \(Y_{ij}^{\nu }\), de bijdrage van de elektron-gat grondtoestandcorrelaties meten \(\hat {a}_{j}^{+}\hat { a}_{i}|\Phi _{0}>\), respectievelijk, tot de excitatie van de aangeslagen toestand |Φ _ν > van frequentie ω _ν .

De overeenkomstige sterkten van de dipooloscillator f _ν worden uitgedrukt in termen van de RPA-amplitudes X ^ν en J ^ν ,

$$ f_{\nu} =\frac{2 m_{e}^{*} D^{2}_{\nu}\omega_{\nu}}{\hbar^{2}}, \quad D_{ \nu} =\sum_{ij} \left(X^{(\nu)}_{ij} d_{ij} + Y^{(\nu)}_{ij} d_{ji} \right), $ $ (9)

waar d _ij =〈ik |z |j 〉 zijn de dipoolmatrixelementen van één deeltje.

De doorsneden van de fotoabsorptie zijn verkregen door de berekende verdeling van de oscillatorsterkte door Lorentz-profielen te verbreden met een vouwbreedte van 0,2 ω . Fotoabsorptiespectra samen met oscillatorsterkteverdelingen voor NC's met N =8 (a), 32 (b), 50 (c) en 128 (d) elektronen worden getoond in Fig. 2. In Fig. 2d vergelijken we de berekende fotoabsorptiedwarsdoorsnede met de experimentele gegevens van Ref. [21] voor ZnO NC met R 6 nm. Men kan zien dat in alle beschouwde NC's de spectra worden gedomineerd door een enkele resonantielijn, welke positie feitelijk het maximum van de fotoabsorptiedwarsdoorsnede bepaalt. Het is inderdaad te verwachten omdat het elektronische spectrum van één deeltje vergelijkbaar is met een kwantumrotator. De sterkste overgangen gebeuren voor een maximale golffunctie die overlapt, d.w.z. met een gelijk radiaal kwantumgetal n . In ons geval is er maar één zo'n optische overgang van de hoogste bezette toestand j =(1,l _max ) naar de laagste leegstand i =(1,l _max +1). De corresponderende dipool-excitatie verschilt echter sterk van de niet-interagerende overgang van één deeltje wanneer een sterke Coulomb-afstoting elektronencorrelaties belangrijk en overweldigend maakt. Dit is het geval wanneer R ≫een ₀ . Namelijk de energie van collectieve opwinding, ω _ν , overtreft de energie van de overgang van één deeltje

$$ \Delta =\left(\epsilon_{1, l_{max}+1} -\epsilon_{1, l_{max}}\right)=\frac{\hbar^{2} (l_{max}+ 1)}{m_{e}^{*}{\langle r \rangle}^{2}}. $$ (10)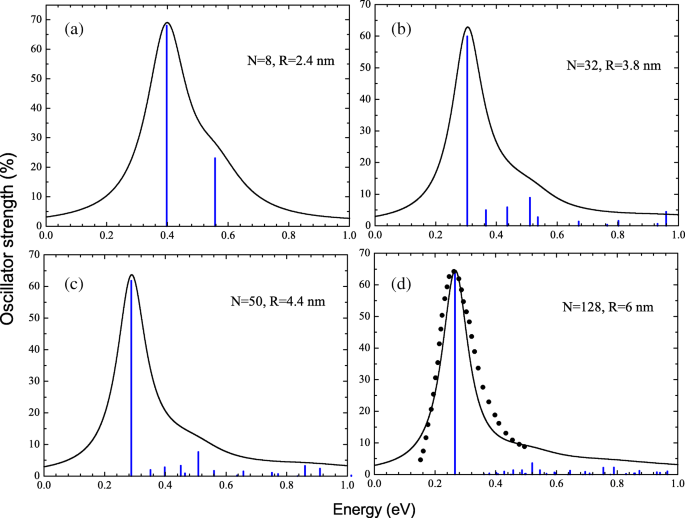

Oscillatorsterkteverdelingen en bijbehorende fotoabsorptiepiekprofielen berekend binnen de RPAE-benadering voor NC's met N =8 (een ), 32 (b ), 50 (c ), en 128 (d ) geleidingsband elektronen. Vergelijking van experimentele [21] (zwarte vierkantjes) en berekende (ononderbroken lijn) resonantiepiekprofielen voor NC met R ≈6 nm (d )

In Fig. 3 vergelijken we de posities van de fotoabsorptiemaxima, ω _res , hier berekend (blauwe cirkels) met experimentele resultaten van [21] (rode sterren). Men neemt een opmerkelijke overeenkomst waar tussen experimentele gegevens en onze theoretische resultaten. Ter vergelijking plotten we hier ook de energieën Δ overgang van één deeltje (groene vierkantjes). Elektronencorrelaties verhogen de collectieve excitatie-energie aanzienlijk in vergelijking met Δ . Een eenvoudige analyse van RPA Eq. (7) verklaart deze waarneming. Als we alleen de belangrijkste optische overgang van j . beschouwen =(1,l _max ) tot j =(1,l _max +1) stelt, de RPA Eq. (7) reduceert tot een 2×2 matrixvergelijking, welke eigenwaarde ω is gewoon:

$$ \omega^{2}=\Delta^{2} +2V\Delta, $$ (11)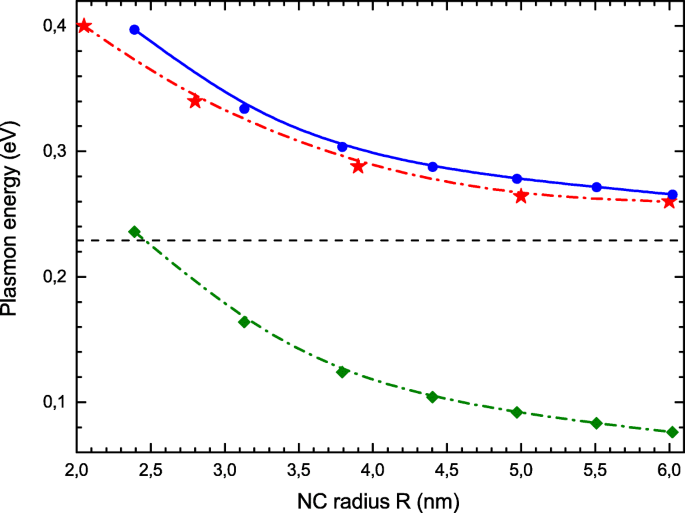

Grootte-afhankelijkheid van LSPR-energie. Experimentele waarden [21] (rode sterren), RPA met lokale uitwisseling (blauwe cirkels), energieën van overgang van één deeltje (groene diamanten in onderste curve). Klassieke waarde (13) wordt weergegeven door de horizontale stippellijn

waarbij \(V=\links \langle ij\left | \hat {v}\right | ij\right \rangle \) het RPA Coulomb-matrixelement aangeeft. De eerste term in de r.h.s. van Verg. (11) geeft de bijdrage van één deeltje, terwijl de tweede term het resultaat is van interacties tussen deeltjes en gaten. Hun verhouding kan worden geschat door de radiale coördinaat van het elektron aan het oppervlak te nemen, r =R in het RPA-matrixelement V , en het verwaarlozen van de ruiltermijn. Deze schatting levert

$$ \frac{2V}{\Delta} \simeq \frac{4R\varepsilon_{i}}{a_{0}(\varepsilon_{i}+2\varepsilon_{m})} \simeq \frac{2R} {a_{0}}. $$ (12)

De bijdrage van elektronencorrelaties domineert dus als R ≫een ₀ . In de limiet van grote NC's is de verdeling van de elektronendichtheid geconcentreerd op het NC-oppervlak; daarom, volgens Vgl. (12), de resonantie-energie in Vgl. (11) heeft de neiging om

$$ \omega =\sqrt{\frac{2\hbar^{2}e^{2}N}{m_{e}^{*}(\varepsilon_{i}+2\varepsilon_{m})R^ {3}}}, $$ (13)

die precies samenvalt met de klassieke dipoolplasmonfrequentie in dunne bolvormige schil [37]. Deze plasmonmodus komt overeen met een tangentiële elektronentrilling. Op deze manier is het vergelijkbaar met de oppervlakteplasmonresonantie in C ₆₀ moleculen, waarbij de resonantiefrequentie goed wordt beschreven door de vergelijking analoog aan Vgl. (13) [38]. Merk op dat, net als het geval van fullereen [39], deze plasmonmodus tweederde van de totale oscillatiesterkte verzamelt (zie figuur 2). Het gebeurt omdat deze oscillatie alleen de hoekgraden van vrijheid omvat, waardoor de radiale beweging onverstoord blijft.

In tegenstelling tot de bekende dipooloppervlakplasmonmodus in homogene sferen, die puur translationeel is, is de huidige overwegingsmodus compressief. De geïnduceerde dichtheid produceert een elektrisch veld evenwijdig aan het oppervlak dat de rol speelt van het herstellen van kracht voor deze plasmonmodus. Bovendien draagt ​​de puur kwantumvariatie van het lokale Fermi-niveau als gevolg van geïnduceerde dichtheidsoscillaties bij aan de herstelkracht. De corresponderende kwantumdrukbijdrage aan de resonantiefrequentie wordt gegeven door de Δ termijn in vgl. (11). Het is kleiner dan de Coulomb-bijdrage in alle beschouwde NC's vanwege de kleinheid van de effectieve Bohr-straal a ₀ in ZnO. In NC's met een grotere waarde van a ₀ , kon men de overgang van klassieke dipoolplasmonresonantie naar kwantumopsluitingsregime waarnemen bij R ∼een ₀ . Het is vermeldenswaard dat in het geval van gedoteerde NC's de parameter a ₀ /R die het klassieke/kwantumkarakter van de dipoolresonantie regelt, hangt alleen af ​​van de NC-grootte en is niet afhankelijk van het aantal vrije dragers N .

In Fig. 3 verwijst de horizontale lijn naar de klassieke plasmonresonantie-energie (13). De blauwe verschuiving van de resonantiefrequentie ten opzichte van zijn klassieke waarde wordt veroorzaakt door twee kwantumeffecten, de hierboven besproken kwantumdrukbijdrage en de afname van de gemiddelde elektronenstraal. Dit laatste gebeurt omdat elektronen in het NC-volume worden geduwd als gevolg van kwantumreflectie vanaf de grens, zodat 〈r 〉≃R −2a ₀ . Dit effect verhoogt het matrixelement V wat op zijn beurt de resonantiefrequentie verhoogt. Dit effect kan ruwweg worden gereproduceerd door de NC-straal R . te vervangen in de noemer van Vgl. (13) door 〈r . Volgens verg. (11)–(13), beide effecten zorgen voor de blauwe frequentieverschuiving evenredig met de inverse NC-straal ∝1/R . In numeriek opzicht is de bijdrage van de laatste echter het grootst.

Conclusies

Om deze brief af te sluiten, hebben we een theorie uitgewerkt die de sterke dipoolresonantie die wordt waargenomen in sterk n-gedoteerde colloïdale ZnO NC's mooi voorspelt. Het nieuwe type oppervlakte-dipoolplasmon-excitaties is theoretisch bestudeerd met behulp van een kwantumbenadering met veel lichamen. We hebben aangetoond dat de sterke Coulomb-afstoting in fotogedoteerde ZnO-nanokristallen leidt tot een specifieke elektronendistributie in de grondtoestand, gelokaliseerd in een dunne oppervlaktelaag dicht bij het binnenoppervlak. Wanneer de dipool wordt geëxciteerd, ondersteunt deze elektronische distributie een collectieve plasmonoscillatie die in wezen wordt gevormd door hoekbeweging. Overgang van deze oppervlakteplasmonmodus van het klassieke naar kwantumopsluitingsregime wordt bepaald door een enkele parameter die gelijk is aan de verhouding van nanokristalgrootte tot effectieve Bohr-straal. Elektronenreflectie van de NC-interface vermindert de straal van de elektronische schaal. Bovendien levert de variatie van het lokale Fermi-niveau een extra bijdrage aan de herstelkracht van de plasmonoscillator. Deze kwantumeffecten leiden tot de grootte-afhankelijkheid van de resonantieplasmonfrequentie, wat een opmerkelijke overeenkomst is met experimentele waarnemingen. In de limiet van een grote NC-straal neigt de resonantielijn soepel naar de klassieke plasmonfrequentie van een geladen schil met een oneindig kleine breedte.

Afkortingen

LDA:

Lokale dichtheidsbenadering

LSPR:

Gelokaliseerde oppervlakteplasmonresonantie

NC:

Nanokristal

RPA:

Willekeurige fasebenadering