Magnetisatiedynamiek gemoduleerd door Dzyaloshinskii-Moriya-interactie in de dubbele interface Spin-Transfer Torque Magnetic Tunnel Junction

Abstract

Momenteel zijn magnetische tunnelovergangen met dubbele interface (MTJ's) ontwikkeld voor het verbeteren van de thermische stabiliteitsbarrière op het technologieknooppunt op nanoschaal. Dzyaloshinskii-Moriya-interactie (DMI) bestaat onvermijdelijk in dergelijke apparaten vanwege het gebruik van de zware metalen / ferromagneetstructuren. Eerdere studies hebben het nadelige effect van DMI op de conventionele single-interface spin-transfer torque (STT) MTJ's aangetoond. Hier, in dit werk, zullen we bewijzen dat het nadelige effect van DMI bijna zou kunnen worden geëlimineerd in de STT-MTJ met dubbele interface. Deze conclusie wordt toegeschreven aan het onderdrukkende effect van Ruderman-Kittel-Kasuya-Yosida (RKKY) interactie op de DMI. Gedetailleerde mechanismen worden geanalyseerd op basis van de theoretische modellen en micromagnetische simulatieresultaten. Ons werk benadrukt het belang van een juiste beheersing van de DMI in de composietvrije laag van de STT-MTJ met dubbele interface.

Inleiding

Magnetic Random Access Memory (MRAM) is een van de meest veelbelovende kandidaten voor het niet-vluchtige geheugen van de volgende generatie dankzij het lage stroomverbruik, de hoge dichtheid, de hoge toegangssnelheid, het bijna oneindige uithoudingsvermogen en de goede compatibiliteit met CMOS-technologie [1, 2]. Het elementaire apparaat van de MRAM is de magnetische tunnelovergang (MTJ), die is samengesteld uit een tunnelbarrière die is ingeklemd tussen twee ferromagnetische lagen (genaamd vastgezette laag en vrije laag). Profiteren van de vooruitgang in de loodrechte anisotropie, is de kenmerkgrootte van de MTJ geschaald onder 40 nm of zelfs 1 × nm [3,4,5]. Een uitdaging voor de sub-40 nm MTJ is echter om de adequate thermische stabiliteitsbarrière E te behouden. = μ ₀ M _s H _k V /2. (met μ ₀ de vacuüm magnetische permeabiliteit, M _s de verzadigingsmagnetisatie, H _k het anisotropieveld, V het volume van de vrije laag). Zoals aangegeven door deze vergelijking, E neemt af met de schaal van de MTJ, wat resulteert in een vermindering van de bewaartijd van gegevens. Om deze uitdaging te overwinnen, werden MTJ's met dubbele interface voorgesteld voor het behalen van voldoende hoge E op het sub-40 nm technologieknooppunt [6,7,8,9,10]. Door twee gekoppelde ferromagnetische lagen te gebruiken als de vrije composietlaag, wordt het equivalente volume (V ) in de dubbele interface MTJ wordt verhoogd om de thermische stabiliteitsbarrière te verbeteren. Ondertussen wordt de dempingsconstante verlaagd om een lage schakelstroom te behouden.

In de MTJ's met dubbele interface speelt de ferromagneet/heavy-metal (FM/HM) structuur een belangrijke rol bij het optimaliseren van de prestaties. Aan de ene kant verhoogt de FM/HM-structuur de spin-orbit-koppeling (SOC) om de loodrechte anisotropie te induceren. Aan de andere kant werkt het zware metaal als een afstandhouder tussen twee ferromagnetische lagen van de vrije composietlaag om de Ruderman-Kittel-Kasuya-Yosida (RKKY) interactie [11] te verschaffen, die de magnetisaties van de twee ferromagnetische lagen in zodat ze zich als een identieke laag gedragen. Bovendien tonen recente werken aan dat de sterke SOC van het zware metaal in combinatie met de atomaire spins van de ferromagneet een antisymmetrische uitwisselingskoppeling zou kunnen vormen, genaamd Dzyaloshinskii-Moriya-interactie (DMI) [12, 13]. Daarom wordt de DMI op natuurlijke wijze geïnduceerd in de MTJ met dubbele interface met FM/HM-structuren. DMI geeft de voorkeur aan de chirale magnetische texturen (bijv. Spin spiralen, skyrmionen en Neel-type domeinwanden) en heeft een dramatische invloed op de magnetisatiedynamiek, zoals gevalideerd door de recente studies [14,15,16,17,18,19,20,21 ,22,23,24,25]. Het is belangrijk om te vermelden dat de rol van DMI gecompliceerder zal worden in de MTJ met dubbele interface, aangezien twee FM/HM-interfaces moeten worden beschouwd samen met een extra RKKY-interactie. Daarom is het van belang om het effect van DMI op de MTJ met dubbele interface te onthullen.

In deze brief bestuderen we voor het eerst het schakelproces van de MTJ's met dubbele interface onder de acties van DMI en RKKY-interactie. De MTJ met dubbele interface wordt geschakeld door het spin-transfer koppel (STT), wat een gangbare benadering is voor het schrijven van gegevens van de MRAM. Onlangs werd gemeld dat de DMI een nadelig effect heeft op de STT-switching [21, 22]. Hier laten onze resultaten zien dat in MTJ's met dubbele interface het nadelige effect van DMI kan worden onderdrukt door RKKY-interactie, wat resulteert in een snelle schakeling en meer uniforme dynamiek. Ons werk bewijst de robuustheid van de STT-MTJ met dubbele interface tegen het negatieve grensvlak-effect.

Methoden

Het apparaat dat in dit werk wordt bestudeerd, wordt geïllustreerd in figuur 1a, met een FM / HM / FM-structuur als de samengestelde vrije laag. De dikte van de HM-laag wordt aangepast aan een geschikte waarde zodat de geïnduceerde RKKY-interactie twee FM-lagen ferromagnetisch koppelt. Een van de FM-lagen is magnetisch zachter, wat wordt aangeduid als FL1 (vrije laag 1), terwijl de andere magnetisch harder is en wordt aangeduid als FL2 (vrije laag 2). Om de magnetisatie van de vrije composietlaag om te schakelen, wordt een stroom toegepast op de MTJ met dubbele interface en genereert deze de STT. In dit werk beschouwen we alleen de verzonden STT van referentielaag naar FL1, terwijl de andere koppels tussen FL1 en FL2 worden verwaarloosd. Dit vereenvoudigde model is consistent met de eerder gerapporteerde werken [26,27,28]. De DMI's worden geïnduceerd in zowel FM/HM- als HM/FM-interfaces en hebben de tegenovergestelde tekens vanwege de verschillende chiraliteit [29].

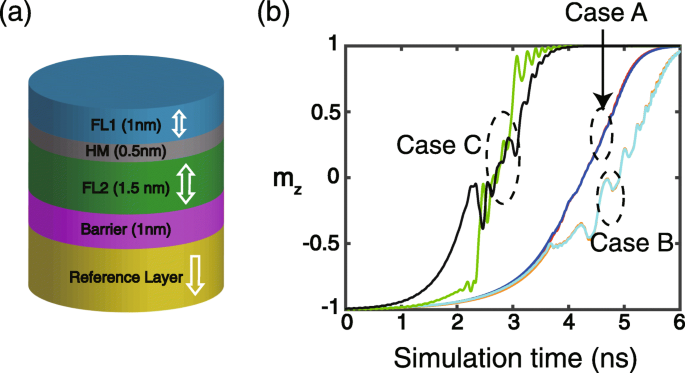
een Schematische structuur van het in dit werk bestudeerde apparaat. De andere lagen zijn voor de duidelijkheid niet getoond. b Typische resultaten van de tijdsafhankelijke m _z (loodrecht-component van de eenheidsmagnetisatie). Geval A:σ = 1 × 10⁻³ J/m² , D ₁ =D ₂ = 0 (rood voor FL1, blauw voor FL2). Geval B:σ = 1 × 10⁻³ J/m² , D ₁ = 1 mJ/m² , D ₂ =−1 mJ/m² (oranje voor FL1, cyaan voor FL2). Geval C:σ = 1 × 10⁻⁴ J/m² , D ₁ =D ₂ = 0 (groen voor FL1, zwart voor FL2)

De magnetisatiedynamiek van de FL1 en FL2 in de MTJ met dubbele interface wordt bestudeerd door micromagnetische simulatie. De tijdsevolutie van de eenheidsmagnetisatievector wordt bepaald door de volgende Landau-Lifshitz-Gilbert (LLG) vergelijking. We kiezen voor het OOMMF-pakket, een open-source micromagnetische simulatietool [30], om de apparaatstructuur te modelleren en de LLG-vergelijking op te lossen voor het analyseren van de magnetisatiedynamiek.

$$ \frac{\partial \mathbf{m}}{\partial t}=-\gamma \mathbf{m}\times {\mathbf{H}}_{eff}+\alpha \mathbf{m}\times \frac{\partial \mathbf{m}}{\partial t}+\gamma \frac{\mathrm{\hslash}}{2e}\frac{\eta }{M_s{t}_F}J\mathbf{m }\times \left(\mathbf{m}\times \mathbf{z}\right) $$

waar γ is de gyromagnetische verhouding, m is de eenheidsvector langs de magnetisatie, z is de eenheidsvector langs de dikterichting, H _eff is het effectieve veld inclusief uniaxiale loodrechte anisotropie, 6-buren uitwisselingsenergie, DMI-veld, RKKY-interactie, demagnetisatieveld, dipolaire interactie en STT. Andere parameters en hun standaardwaarden staan vermeld in Tabel 1, tenzij anders vermeld. Deze parameterwaarden zijn in overeenstemming met de modernste technologieën. Wat betreft de DMI-magnitude beschouwen we een CoFeB/W/CoFeB-composietvrije laag in de MTJ met dubbele interface [10, 31,32,33]. De gerapporteerde experimentele DMI-resultaten van W/CoFeB variëren van 0,12 mJ/m² tot 0,73 mJ/m² [34,35,36]. In onze simulatie breiden we het bereik van de DMI-magnitude uit tot ±2 mJ/m² voor een algemene studie.

De RKKY-energie tussen een paar magnetische momenten m _ik en m _j is gedefinieerd als E _ij = σ [1 − m _ik ∙ m _j ]/∆ _ij , waar m _ik en m _j zijn magnetische momenten van respectievelijk FL1 en FL2. σ is de bilineaire oppervlakte-uitwisselingscoëfficiënt tussen twee oppervlakken. ∆ _ij is de discretie celgrootte in de richting van cel i richting cel j . In dit werk zijn FL1 en FL2 ferromagnetisch gekoppeld, dan σ> 0 wat betekent dat de RKKY-interactie de neiging heeft om m . te maken _ik parallel aan m _j . De DMI werkt in op de naburige atoomspins S ₁ en S ₂ door een derde atoom met een grote SOC. Overeenkomstige DMI Hamiltoniaan wordt uitgedrukt als H _DM = − D ₁₂ ∙ (S ₁ × S ₂ ), waar D ₁₂ is de DMI-vector [37]. Daarom verslechtert de DMI de uniformiteit tussen S ₁ en S ₂ , die concurreert met de RKKY-interactie.

Resultaten en discussie

Allereerst typische simulatieresultaten van de tijdafhankelijke m _z (loodrechte component van de eenheidsmagnetisatie) worden getoond in Fig. 1b. Als de RKKY-interactie voldoende sterk is (bijv. σ = 1 × 10⁻³ J/m ² in geval A en geval B), zijn FL1 en FL2 aan elkaar gekoppeld en dus is hun magnetisatiedynamiek bijna identiek, ongeacht of de DMI wordt overwogen of niet. Er wordt ook gezien dat de introductie van DMI het proces van de magnetisatieomschakeling verstoort (zie geval B), wat in overeenstemming is met de gerapporteerde resultaten [21,22,23] en kan worden toegeschreven aan de antisymmetrische uitwisseling van DMI. Zodra de RKKY-interactie niet sterk genoeg is, kan de magnetisatiedynamiek van FL1 en FL2 niet ideaal worden gekoppeld, zodat er een significant verschil tussen beide wordt waargenomen (zie geval C). Hieronder worden de simulatieresultaten verkregen onder een voldoende sterke RKKY-interactie, tenzij anders vermeld.

Daarna bestuderen we de schakelsnelheid onder de verschillende RKKY-interacties. De schakelsnelheid wordt weergegeven door een tijdstip waarop m _z bereikt 0 (gedefinieerd als de schakeltijd). De D ₁ en D ₂ zijn ingesteld op respectievelijk positieve en negatieve waarden [29]. De overeenkomstige resultaten worden getoond in Fig. 2. Bij afwezigheid van DMI neemt de schakeltijd toe met de verbeterde RKKY-interactie, in overeenstemming met de andere gerapporteerde resultaten [26,27,28, 38]. De reden is dat de sterkere RKKY-interactie de magnetisatiedynamiek van FL1 en FL2 coherenter maakt, wat op equivalente wijze de anisotropie van de vrije composietlaag verhoogt. De afhankelijkheid van de schakeltijd van de RKKY-sterkte wordt echter chaotischer in aanwezigheid van DMI. Deze chaos wordt voornamelijk toegeschreven aan de inconsistentie van de anisotropie tussen FL1 en FL2. Meer uitleg volgt later. Deze resultaten bewijzen het niet te verwaarlozen effect van DMI op het schakelgedrag van de MTJ met dubbele interface.

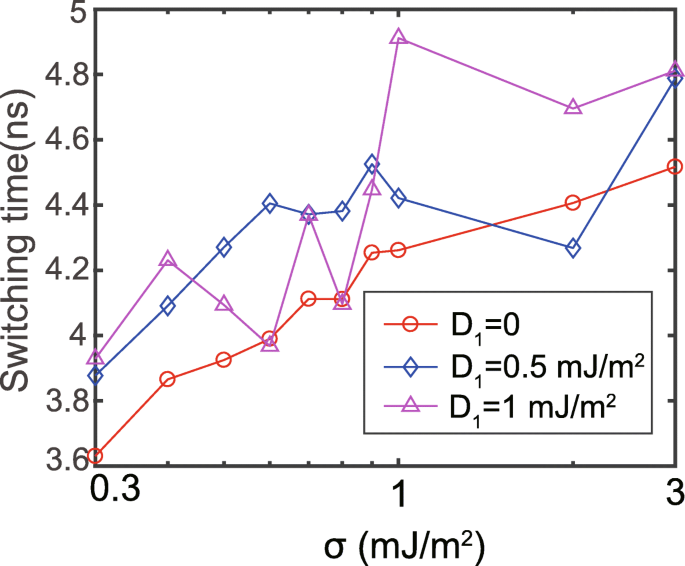
Schakeltijd als functie van RKKY-sterkte, met σ op de logaritmeschaal. D ₁ en D ₂ zijn ingesteld op dezelfde waarden, maar met de tegenovergestelde tekens

Vervolgens bestuderen we het effect van DMI in meer detail. Figuur 3 toont de schakeltijd als functie van de DMI-sterkte. Het is belangrijk om te vermelden dat D ₁ en D ₂ zijn opzettelijk ingesteld op dezelfde positieve waarden in figuur 3a, hoewel ze in werkelijkheid de tegenovergestelde tekens hebben. Met andere woorden, figuur 3a komt overeen met een virtueel geval, dat we bestuderen om het simulatiemodel te verifiëren. Vanuit het gezichtspunt van de fysische theorie worden de nadelige effecten van twee positieve DMI's gecumuleerd onder de werking van ferromagnetisch gekoppelde RKKY-interactie. Daarom wordt verwacht dat de schakeltijd zal toenemen met de toenemende D ₁ en D ₂ , zoals gerapporteerd in de vorige werken [21, 22]. Deze analyse komt goed overeen met de resultaten getoond in figuur 3a. Zo wordt de rationaliteit van het simulatiemodel gevalideerd. In tegenstelling tot figuur 3a zouden de nadelige effecten van DMI kunnen worden verzacht als D ₁ en D ₂ hebben de tegenovergestelde tekens, zoals weergegeven in figuur 3b, waar de variatie van de schakeltijd veel kleiner is in vergelijking met figuur 3a. Merk op dat in figuur 3b de curve niet bepaald eentonig is, de lokale fluctuatie zal later worden uitgelegd. Opmerkelijk is dat de effecten van DMI's op twee interfaces teniet kunnen worden gedaan door de magnitudes van D op de juiste manier af te stemmen. ₁ en D ₂ , zoals getoond in Fig. 3c. Deze resultaten kunnen als volgt worden verklaard in termen van chiraliteitstheorieën.

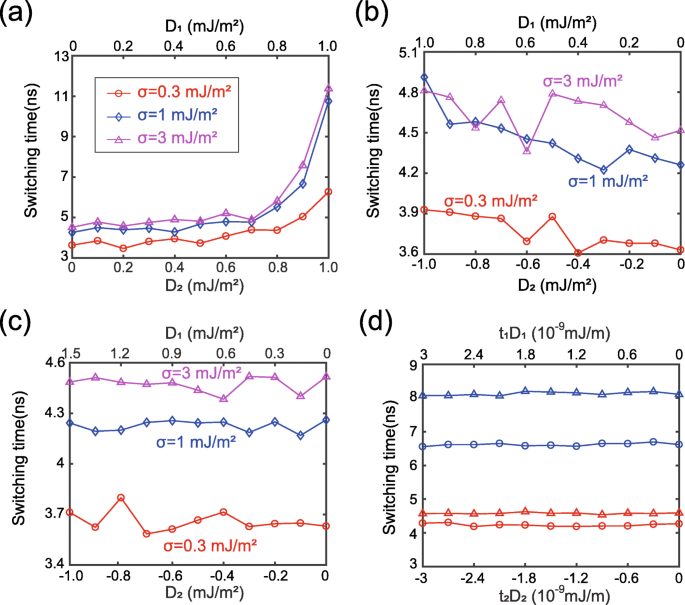
Schakeltijd als functie van DMI-sterkte. een D ₁ en D ₂ worden op dezelfde positieve waarde ingesteld. b D ₁ en D ₂ zijn ingesteld op dezelfde waarde, maar met de tegenovergestelde tekens. c D ₁ en D ₂ zijn geconfigureerd om te voldoen aan t ₁ D ₁ + t ₂ D ₂ = 0. d Aanvullende resultaten terwijl de dikte of anisotropie constant wordt gewijzigd, terwijl t . behouden blijft ₁ D ₁ + t ₂ D ₂ = 0. blauwe lijn:t ₁ wordt gewijzigd in 2 nm; rode lijn:t ₁ wordt gewijzigd in 1,5 nm. Driehoeksgegevens:σ = 3 × 10⁻³ J/m² . Cirkelgegevens:σ = 1 × 10⁻³ J/m²

De DMI-energie wordt uitgedrukt als E _DM = t ∬ D [m _x (∂m _z /∂x ) − m _z (∂m _x /∂x ) + m _j (∂m _z /∂y ) − m _z (∂m _j /∂y )]d ² r = tDε _DM [39], waar D is de continue DMI-constante, t is de dikte van de ferromagnetische laag. Zoals hierboven vermeld, is de magnetisatiedynamiek van FL1 en FL2 bijna identiek onder een voldoende sterke RKKY-interactie. In dit geval dezelfde ε _DM wordt verkregen in FL1 en FL2. Dan kan de totale DMI-energie van FL1 en FL2 worden berekend met E _tot = (t ₁ D ₁ + t ₂ D ₂ )ε _DM . Daarom, door D . in te stellen ₁ /D ₂ = − t ₂ /t ₁ , zouden de DMI-effecten van FL1 en FL2 volledig kunnen worden gecompenseerd in het geval van een voldoende grote σ, in overeenstemming met figuur 3c. Deze conclusie wordt verder bevestigd door de aanvullende resultaten die worden getoond in Fig. 3d, waar de andere parameters opzettelijk worden gevarieerd terwijl D behouden blijft. ₁ /D ₂ = − t ₂ /t ₁ .

De equivalente DMI-magnitude (D _eq ) van de vrije composietlaag kan worden uitgedrukt als D _eq = (t ₁ D ₁ + t ₂ D ₂ )/(t ₁ + t ₂ ), die zou kunnen worden gebruikt voor het kwantitatief analyseren van het effect van DMI op de MTJ met dubbele interface. Om de effectiviteit van deze vergelijking te valideren, tonen we twee groepen simulatieresultaten in Fig. 4a, waar twee curven werden verkregen onder dezelfde D _eq maar met twee paar verschillende {D ₁ ,D ₂ } waarden, respectievelijk. Hoewel er een klein verschil is tussen de twee curven, zijn hun algemene trends vergelijkbaar en valideren ze het nadelige effect van DMI op de STT-omschakeling. Hier zou het verschil tussen twee curven als volgt kunnen worden verklaard. FL1 en FL2 hebben verschillende anisotropieconstanten, wat leidt tot de lokale onzekere oscillatie van de magnetisatiedynamiek, zoals weergegeven in figuur 4c. Hetzelfde fenomeen wordt ook waargenomen in Fig. 2 en Fig. 3b. In plaats daarvan wordt een ideaal geval getoond in Fig. 4b, d, waar de anisotropieconstanten van FL1 en FL2 op dezelfde waarden zijn ingesteld. Het is duidelijk dat er een goede overeenkomst tussen de twee curven wordt gezien, wat aangeeft dat de bovenstaande uitdrukking van D _eq zou het equivalente DMI-effect van de MTJ met dubbele interface goed kunnen beschrijven.

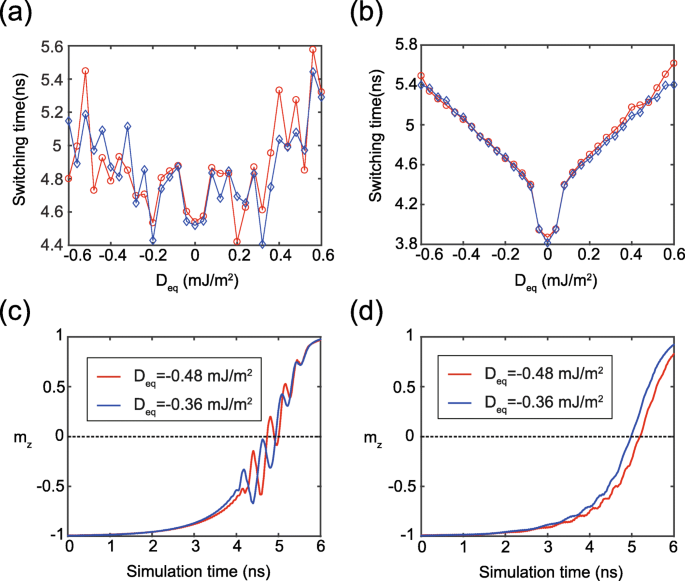
een , b Schakeltijd als functie van D _eq . Elke D _eq wordt verkregen met twee paar verschillende {D ₁ ,D ₂ } waarden volgens D _eq = (t ₁ D ₁ + t ₂ D ₂ )/(t ₁ + t ₂ ). Rode curve:D ₁ is ondertussen gevarieerd D ₂ is vastgesteld op 1 mJ/m² . Blauwe curve:D ₁ en D ₂ worden altijd op dezelfde waarde ingesteld. Hier σ = 1 × 10⁻² J/m² . In een , zijn de andere parameters geconfigureerd als Tabel 1. In b , K _{u 1} = K _{u 2} = 0,7 mJ/m³ voor een ideaal geval. c , d Typische resultaten van tijdsafhankelijke m _z overeenkomend met a en b , respectievelijk

Ten slotte analyseren we de tijdsevolutie van de magnetisatiedynamiek in meer detail. Figuur 5 toont de tijdsafhankelijke energie tijdens het schakelen van magnetisatie. De DMI-energieën van de FL1 en FL2 worden verzameld of geannuleerd, afhankelijk van de tekens en groottes van D ₁ en D ₂ . Deze trend komt goed overeen met de bovenstaande theoretische modellen. Bovendien worden de RKKY-energieën op lage waarden gehouden, wat bevestigt dat de magnetische momenten van FL1 en FL2 synchroon worden aangedreven. De verdelingen van RKKY- en DMI-velden worden getoond in Fig. 6, waar RKKY-veld in verschillende gevallen verschillende rollen speelt. Ten eerste, in het geval van een niet-nul DMI (zie geval 2 en geval 3), is het RKKY-veld veel sterker in vergelijking met het geval van nul DMI (zie geval 1). Het zou duidelijk kunnen zijn dat het RKKY-veld de extra niet-uniformiteit van de magnetische texturen in aanwezigheid van DMI moet overwinnen. Ten tweede, als D ₁ en D ₂ van de tegenovergestelde tekens zijn, weerstaat het RKKY-veld de DMI-velden in zowel FL1 als FL2 (zie geval 2). Als gevolg hiervan wordt de DMI verzwakt, zodat de magnetisatiedynamiek uniformer wordt. In tegenstelling, eenmaal D ₁ en D ₂ hetzelfde teken hebben, weerstaat het RKKY-veld het DMI-veld in de ene ferromagnetische laag, maar helpt het in de andere ferromagnetische laag (zie geval 3). Het totale DMI-veld heeft dus nog steeds een bepaald effect op de magnetisatiedynamiek, wat bevestigt dat de DMI niet kan worden opgeheven als D ₁ en D ₂ zijn van hetzelfde teken.

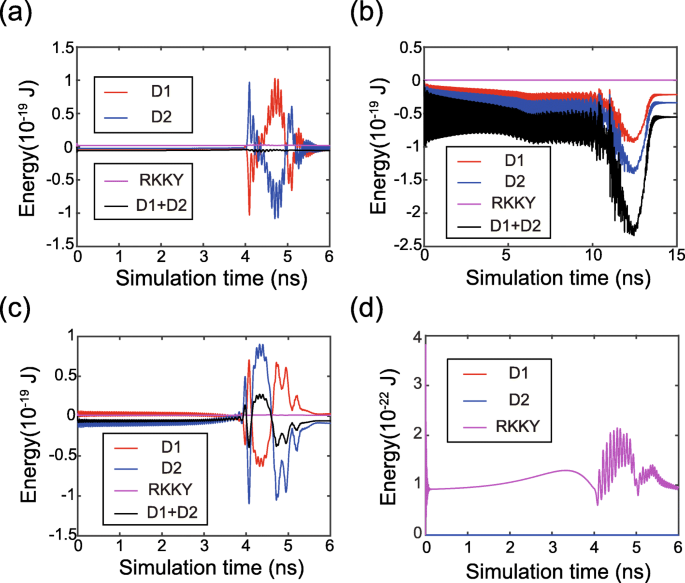
Tijdsevolutie van de DMI- en RKKY-energieën. een D ₁ = 1,5 mJ/m² , D ₂ = − 1 mJ/m² , d.w.z. het DMI-effect wordt opgeheven. b D ₁ = D ₂ = 1 mJ/m² , d.w.z. het DMI-effect wordt geaccumuleerd. c D ₁ = 1 mJ/m² , D ₂ = − 1 mJ/m² , d.w.z. het DMI-effect wordt verzacht maar niet tenietgedaan. d D ₁ = D ₂ = 0

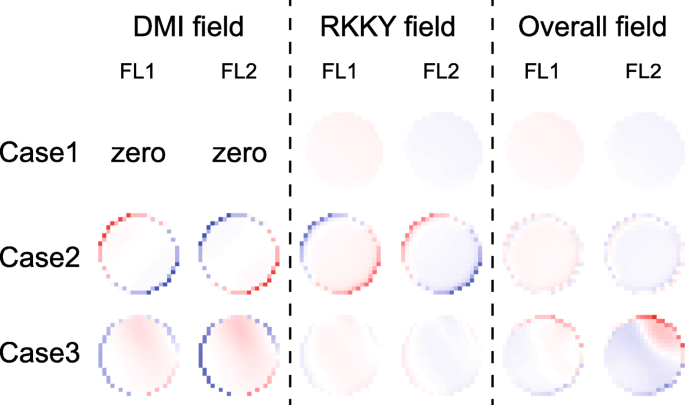
Ruimtelijke verdelingen van de DMI- en RKKY-velden. Hier wordt voor elk geval een typisch resultaat op een bepaald moment getoond. Op de andere tijdstippen blijft de conclusie ongewijzigd. Geval 1:D ₁ = D ₂ = 0. Geval 2:D ₁ = 1,5 mJ/m² , D ₂ = − 1 mJ/m² , d.w.z. het DMI-effect wordt opgeheven. Geval 3:D ₁ = D ₂ = 1 mJ/m² , d.w.z. het DMI-effect wordt geaccumuleerd

Figuur 7 toont de micromagnetische configuraties van de FL1 en FL2 tijdens de magnetisatieschakeling. Hoewel de domeinmuur in alle gevallen verschijnt, kunnen op sommige momenten verschillende kenmerken worden waargenomen. Het is algemeen bekend dat de DMI de voorkeur geeft aan niet-uniforme magnetische texturen. Niettemin wordt in Fig. 7 nog steeds uniforme magnetisatie gevormd, zelfs in de aanwezigheid van DMI (zie de tijd waarop m _z = − 0,5 in geval 2), zolang het DMI-effect wordt opgeheven. Nogmaals, dit resultaat valideert het bovenstaande theoretische model. Bovendien wordt ook gezien dat de magnetisatiedynamiek meer niet-uniform is als D ₁ en D ₂ zijn van hetzelfde teken (zie geval 3 waar de domeinmuur altijd verschijnt), consistent met de bovenstaande analyse. We laten ook enkele resultaten zien die zijn gesimuleerd met kleinere MTJ (zie de laatste twee rijen in Fig. 7). Het verschil in micromagnetische configuraties tussen geval 2 (DMI wordt opgeheven) en geval 3 (DMI wordt niet opgeheven) is opvallender.

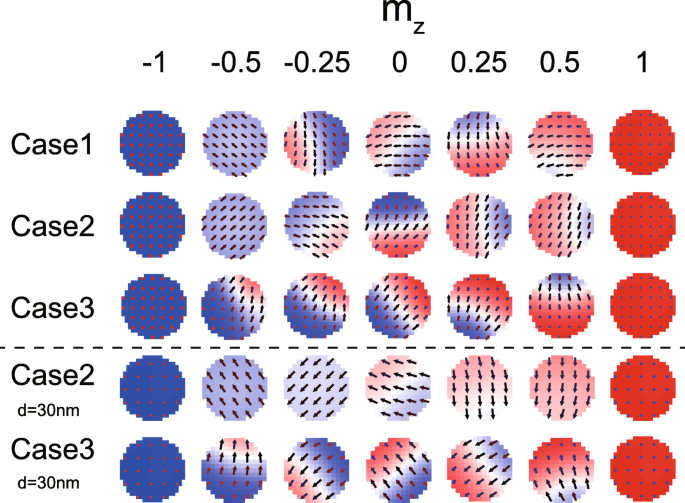
Micromagnetische configuraties tijdens de magnetisatieschakeling. Hier worden gevallen 1~3 geconfigureerd met dezelfde parameters als in Fig. 6

Conclusie

We hebben het effect van DMI op de STT-MTJ met dubbele interface uitgebreid bestudeerd. Zoals bekend is de MTJ met dubbele interface ontwikkeld om de thermische stabiliteitsbarrière te verbeteren. In dit werk bewijzen onze resultaten een ander voordeel van MTJ met dubbele interface, dat wil zeggen, het onderdrukken van het nadelige effect van DMI. De DMI's in twee ferromagnetische lagen kunnen worden onderdrukt of zelfs teniet worden gedaan als ze worden geconfigureerd met de juiste waarden en tegengestelde tekens, waaraan natuurlijk wordt voldaan door de STT-MTJ-structuur met dubbele interface. Theoretische modellen werden voorgesteld om de conclusie te verklaren. Micromagnetische simulatieresultaten werden besproken om de rol van DMI in de magnetisatiedynamiek te onthullen. Ons werk biedt een haalbare benadering om de DMI in de STT-MTJ met dubbele interface te minimaliseren.

Beschikbaarheid van gegevens en materialen

Alle gegevens zijn onbeperkt beschikbaar.

Afkortingen

DMI:: Dzyaloshinskii-Moriya interactie
FL:: Gratis laag
FM/HM:: Ferromagneet/zware metalen
MRAM:: Magnetisch willekeurig toegankelijk geheugen
MTJ:: Magnetische tunnelverbinding
RKKY:: Ruderman–Kittel–Kasuya–Yosida
SOC:: Spin-baan koppeling
STT:: Spin-overdracht koppel

Protoporfyrine IX-geladen laminarine-nanodeeltjes voor de behandeling van kanker, hun cellulaire gedrag, ROS-detectie en dierstudies Synergetisch verbeterde remmende effecten van door pullulan nanodeeltjes gemedieerde co-afgifte van lovastatine en doxorubicine aan triple-negatieve borstkankercellen

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal