Evolutie van het contactgebied met normale belasting voor ruwe oppervlakken:van atomaire naar macroscopische schalen

Methoden

Rough Fractal Surface Generation

Om het contactgedrag van het ruwe oppervlak te bestuderen, moeten we het oppervlak voor het numerieke model genereren. Er zijn verschillende algoritmen gebruikt voor fractale oppervlakken [24]. In dit werk gebruiken we de Fourier-transformatiemethode om fractale ruwe oppervlakken te genereren, zoals te zien is in Fig. 1. Er zijn vier parameters vereist om de fractale ruwe oppervlaktegeometrie te bepalen. Dit zijn de maximale frequentie (w _H ), de minimale frequentie (w _L ), de Hurst-exponent (H ), en de standaarddeviatie van de amplitude (P ). De statistische basisparameters van het oppervlak, zoals RMS (root mean square) hoogte \( \left(\sqrt{M_0}\right) \), RMS slope \( \left(\sqrt{M_2}\right) \) _, en RMS-kromming \( \left(\sqrt{M_4}\right) \), zijn de belangrijkste parameters voor het gedrag van de interface, waarbij M _ik is de i e radiale moment van het oppervlaktespectrum [19, 20]. Het is vermeldenswaard dat de statistische oppervlakteparameter M _ik is gerelateerd aan de statistische profielparameters m _ik door de volgende vergelijking:\( {M}_0={m}_0,{M}_2=2{m}_2,{M}_4=\frac{4}{3}{m}_4 \). Het is algemeen bekend dat de aperiteitsdichtheid n (oppervlaktetoppen of -dalen) kan worden bepaald door de volgende vergelijking:

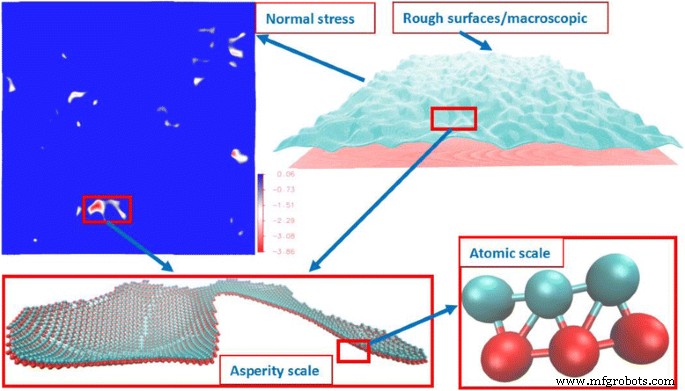
Het GFMD-model op verschillende schalen, van atomaire schaal tot macroscopische schaal (in σ )

Bovendien is het oppervlaktetotaal van de top/vallei N wordt uitgedrukt door

waar A ₀ is het schijnbare oppervlak. Voor het zelf-affiene fractale oppervlak zijn de statistische oppervlakteparameters gerelateerd aan de invoerparameters (w , H , P ) door de volgende vergelijking:

waar B is de oppervlakteruwheidsconstante, die gerelateerd is aan P . De vergelijkingen (3) en (2) geven aan dat het fractale oppervlak van de top/vallei afhankelijk is van de golflengte en de Hurst-exponent. Gedetailleerde besprekingen van de statistische eigenschappen van het fractale oppervlak zijn te vinden in de literatuur [25, 26].

In het Fourier-transformatiealgoritme stellen we als typisch voorbeeld de Hurst-component in op H = 0.5, de maximale frequentie moet w . zijn _L = 1/(24σ ), moet de minimale frequentie w . zijn _H = 1/(256σ ), de standaarddeviatie van de frequentie-amplitude moet P . zijn = 0,69, en de systeemgrootte moet 512 × 512 atomen zijn (met een beginafstand gelijk aan 1,12σ ). Deze invoerparameters genereren vervolgens het oppervlak met de volgende statistische parameters:oppervlak RMS helling \( \sqrt{M_2}=0.077 \) en RMS kromming \( \sqrt{M_4}=0.0077 \) . Het totale aantal oppervlaktetoppen/dalen is 150 gebaseerd op Vgl. (2), terwijl door het getal numeriek te tellen, het topnummer aan de oppervlakte 158 is en het dalnummer 159. De fout is binnen 5%, wat suggereert dat de systeemomvang in statistische zin acceptabel is. In feite, wanneer we de systeemgrootte vergroten tot 2048 × 2048 atomen (met een beginafstand gelijk aan 1,12σ ), komen de resultaten voor de statistische parameters overeen met die van het kleinere systeem.

GFMD-model

Interdeeltjesinteractie is erg moeilijk experimenteel vast te leggen [6, 27]. Onlangs is moleculaire dynamica gebruikt om interactie tussen deeltjes te simuleren, met als doel de moleculaire oorsprong van het contact-/wrijvingsmechanisme te onderzoeken. De rekenkosten zijn echter aanzienlijk hoog voor grootschalige simulaties van moleculaire dynamica. Daarom wordt GFMD geïntroduceerd om het oppervlak te simuleren vanwege zijn hoge efficiëntie. GFMD gebruikt moleculaire dynamica om de interactie van de atomen van de interface te simuleren (twee lagen hier), terwijl de niet-interfacelaag, die meestal elastisch gedrag vertoont, wordt gesimuleerd door de functie van Green. Het reduceert dus het grote atomaire systeem tot tweelaagse atomen aan het grensvlak (zoals te zien in figuur 1), wat de rekenkosten drastisch vermindert. Gedetailleerde besprekingen van GFMD zijn te vinden in de literatuur [21,22,23, 28]. In het GFMD-model wordt de Lennard-Jones (LJ) potentiaal gebruikt om de interactie tussen de deeltjes te simuleren. De vergelijking wordt geschreven als

waar ε is de diepte van de potentiële bron, σ is de eindige afstand waarop de potentiaal tussen de deeltjes nul is, en r is de afstand tussen de deeltjes. We nemen ε , σ , en ε /σ als respectievelijk de eenheid voor energie, afstand en kracht. Volgens het LJ-potentieel weten we dat wanneer r = 2 ^1/6 σ ≈ 1.12σ , de kracht tussen de deeltjes is nul. Wanneer r> 1.12σ , de kracht tussen de deeltjes is aantrekkelijk; wanneer r < 1.12σ , de kracht tussen de deeltjes is afstotend. Aangezien we in dit werk geen rekening houden met adhesie, is de afsnijafstand ingesteld op 1,12σ . De kristalstructuur die voor de atomaire laag wordt gebruikt, is face-centered cubic (FCC). Vanwege de symmetrie nemen we alleen de laag van de interface om de oppervlaktegeometrie te vormen zoals weergegeven in Fig. 1 en het elastische blok onder het platte oppervlak wordt gesimuleerd door de functie van Green.

Contact opnemen met clusterherkenningsmethode

Er zijn drie schalen waargenomen in de interface zoals te zien in figuur 1:(1) atomaire schaal, die wordt gesimuleerd door LJ-potentiaal; (2) scherptediepte, wat het groepseffect is van contactatomen; en (3) macroscopische schaal, wat het groepseffect is van contactclusters. De grootte, vorm, locatie en verdeling van de contactclusters vormen de cruciale brug tussen moleculair gedrag en interface-eigenschappen. Op nanoschaal is het atomaire contactgebied moeilijk te definiëren [6]. We definiëren hier een contactatoom door zijn normaalcomponent kracht fz >  0. Vervolgens worden de verbonden contacterende atomen gedefinieerd als een contacterend cluster. De labeltechniek [29, 30] wordt gebruikt om het contactcluster te doorzoeken. Hier gebruiken we een aangepast algoritme voor versnelling, dat het recursieve zoekproces vermijdt. Het stroomschema van het algoritme wordt getoond in figuur 2, waar atomaire krachtgegevens worden geëxtraheerd uit de moleculaire dynamica-simulatie van de functie van Green. Het algoritme is als volgt onderverdeeld in acht belangrijke stappen.

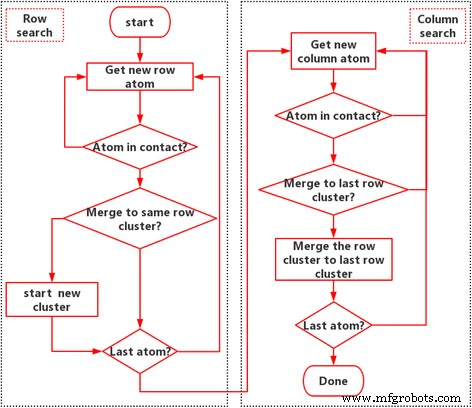
Algoritme voor het detecteren van contactclusters:de labeltechniek

Stap 1. Start het zoeken naar rijen en verkrijg de nieuwe atoomgegevens, dat wil zeggen, doorzoek de atomen van rij tot rij.

Stap 2. Bepaal of het atoom in contact is. Als er geen contact is, ga dan terug naar stap 1. Als het contact maakt, ga dan naar de volgende stap.

Stap 3. Vergelijk het huidige atoom met het vorige atoom in dezelfde rij. Als het vorige atoom ook in contact is, voeg je het atoom samen in de cluster waartoe het vorige atoom behoort en label je het atoom met hetzelfde nummer als het vorige atoom. Als het vorige atoom geen contact maakt, label het atoom dan met een nieuw nummer dat het vorige nummer plus één is.

Stap 4. Bepaal of het het laatste atoom is; zo niet, ga dan terug naar stap 1 of ga naar het zoekproces voor kolommen.

Stap 5. Start de kolomzoekopdracht en verkrijg de nieuwe atoomgegevens, dat wil zeggen, zoek de atomen van kolom tot kolom.

Stap 6. Bepaal of het atoom in contact is. Als er geen contact is, ga dan terug naar stap 5. Als er contact is, ga dan naar de volgende stap.

Stap 7. Vergelijk het huidige atoom met het vorige atoom in dezelfde kolom. Als het vorige atoom ook contact maakt en tot een ander cluster behoort, voeg dan het huidige cluster samen met het cluster waartoe het vorige atoom behoort, label de atomen met hetzelfde nummer en sla ze op. Als het vorige atoom geen contact heeft of tot hetzelfde cluster behoort, ga dan naar de volgende stap.

Stap 8. Bepaal of het huidige atoom het laatste atoom is; zo niet, ga dan terug naar stap 5, of het zoekproces is voltooid.

Numeriek experimenteel ontwerp

Het is algemeen bekend dat het probleem van contact met twee ruwe oppervlakken kan worden vereenvoudigd als een probleem met één samengesteld stijf ruw oppervlak en een plat elastisch oppervlak door de equivalente elastische modulus E* in te voeren. , die is geschreven als

waar E ₁ en E ₂ zijn respectievelijk de elasticiteitsmodulus van het bovenoppervlak en het onderoppervlak. Voor de eenvoud beschouwen we een stijf ruw oppervlak dat in contact komt met een elastisch glad oppervlak en bestuderen vervolgens de vorming en ontwikkeling van het contact makende cluster en zijn kracht-gebiedsgedrag. In de volgende bespreking zullen we het hierboven gegenereerde oppervlak gebruiken (het bovenoppervlak is stijf en ruw (E ₁ = ∞), en het onderoppervlak is glad en elastisch (E ₂ = 3ε /σ ³ )) om het contactgedrag te bestuderen, waarbij beide v ₁ en v ₂ zijn ingesteld op 0,5. Onze systeemgrootte is 512 × 512 atomen (met een beginafstand gelijk aan 1,12σ ), en periodieke randvoorwaarden worden gebruikt in de x -j vlak. De elastische blokdiepte is ingesteld op 1024 atomaire lagen (met een beginafstand gelijk aan 1,12σ ). In een reguliere moleculaire dynamica-simulatie zal het systeem uit 268.697.600 atomen bestaan; het GFMD-model reduceert het aantal tot 524.288 (twee lagen atomen), zoals te zien is in figuur 1. We duwen het ruwe oppervlak (aan de bovenkant) geleidelijk in het platte elastische oppervlak. De belasting van het stijve oppervlak wordt geregeld door de verplaatsing. Elke verplaatsingslaadstap is ingesteld op 0,01σ , en het GFMD-algoritme zal de positie van elk atoom bijwerken totdat de atoomkracht voldoet aan de convergentiecriteria L ¹ -norm = 0.01ε/σ. Het maximale aantal herhalingen is ingesteld op 50.000 om een ​​eindeloze lus te voorkomen.

Resultaten en discussie

Contact opnemen met de distributie en ontwikkeling van clusters

Het oneffenheidsmodel beschouwt de ruwheid als bolvormig of elliptisch en houdt geen rekening met de interactie tussen de contactoneffenheden. In dit werk worden de oneffenheden die in het asperity-model worden gebruikt, geëxtraheerd uit het hierboven gegenereerde oppervlak. In het oneffenheidsmodel kunnen de potentiële contactoneffenheden vooraf worden bepaald door de oppervlaktegeometrie op basis van hun hoogte; dat wil zeggen, de toppen/dalen aan het oppervlak zullen zich, afhankelijk van hun hoogte, als contactclusters vormen. In werkelijkheid heeft de oneffenheid echter een onregelmatige vorm en gewoonlijk kunnen verschillende aangrenzende oneffenheden samenvloeien tot een grote, zoals weergegeven in figuur 2. Er wordt waargenomen dat er in het begin zes onafhankelijke oneffenheden zijn, en als contactkracht neemt toe, versmelten ze uiteindelijk tot een groot contactcluster (Fig. 3). Dit suggereert dat de veronderstelling dat de inter-asperity-afstand ver genoeg is om ongelijkheden elkaar niet te laten beïnvloeden, tot onnauwkeurige resultaten kan leiden.

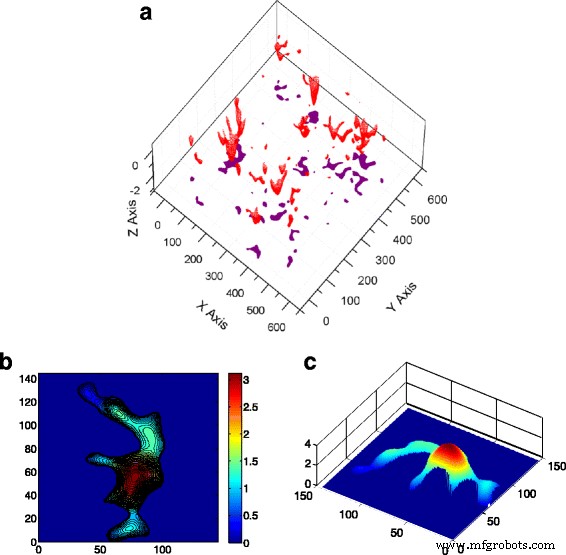
De vorm van de clusters en het samensmeltend effect. een De 3D-weergave van contactclusters en de projectie ervan op de x -j vlak (in σ ). b Een typisch contactcluster bestaande uit zes onafhankelijke ongelijkheden. c De 3D-weergave van de geometrie van het contactcluster (in σ )

Afbeelding 4 laat zien dat het clusternummer eerst toeneemt en vervolgens afneemt naarmate het contactoppervlak groter wordt, terwijl de oneffenheid van het oppervlak altijd toeneemt naarmate het contactoppervlak groter wordt. Dit komt door het samenvoegingseffect dat wordt uitgelegd in Afb. 3.

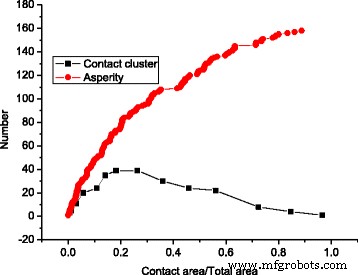
Oppervlaktevalleien en clusternummer onder verschillende contactgebieden

Het samenvoegingseffect van contactclusters is waargenomen in zowel het asperity-model als het GFMD-model. Met hetzelfde contactgebied is het aantal contactclusters in het GFMD-model echter veel groter dan dat van het asperity-model, zoals te zien is in figuur 5. Het is waargenomen dat het aantal contactclusters in het GFMD-model bijna twee keer zo groot is als dat van in het asperity-model, zoals weergegeven in figuur 5. De belangrijkste reden hiervoor is dat het asperity-model geen rekening houdt met de inter-asperity-interactie. In het GFMD-model beïnvloeden de contactclusters elkaar echter. De verplaatsingsvelden die door de contactclusters worden gegenereerd, zijn continu over het hele oppervlak. De verplaatsing van het grote ensemble van clusters resulteert in een nieuwe geometrie op het elastische oppervlak, wat de vorming van nieuwe contactclusters beïnvloedt. Daarom is de vorming van het contactcluster niet alleen gebaseerd op de hoogte van het stijve ruwe oppervlak, maar kan ook worden beïnvloed door vervormingen in het gladde elastische oppervlak. Dit kan ook worden waargenomen in figuur 6, die de distributie van contactclusters op verschillende gebieden voor respectievelijk het asperity-model en het GFMD-model laat zien. Zoals weergegeven in Fig. 6, bij een contactoppervlak van 5%, zijn de contactclusternummers respectievelijk 17 en 34 voor het asperity-model en het GFMD-model, terwijl bij een contactoppervlak van 10% hun contactclusternummers 24 en 52 worden , respectievelijk. Dit suggereert dat de contactclusters in het GFMD-model discreter zijn dan die in het asperity-model. In het GFMD-model is de gemiddelde clustergrootte kleiner, maar de meeste clusters zullen samenvallen met de toppen/dalen, zoals te zien is in figuur 7. Bovendien beschouwt het asperity-model ofwel de valleien ofwel de toppen als potentiële oneffenheden ( afhankelijk van welke kant in contact is). In figuur 8 ontdekten we echter dat naarmate het contactoppervlak groter wordt, zowel de toppen als de valleien met elkaar in contact kunnen komen. In figuur 8 zijn de meeste oneffenheden in contact de oppervlaktedalen wanneer het contactoppervlak klein is. Wanneer het contactoppervlak echter groter is dan 10% van het oppervlak, kunnen zich ook steeds meer toppen vormen als contactclusters.

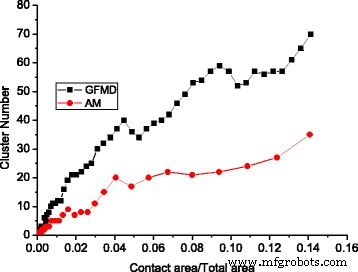
De clusterontwikkeling voor verschillende modellen

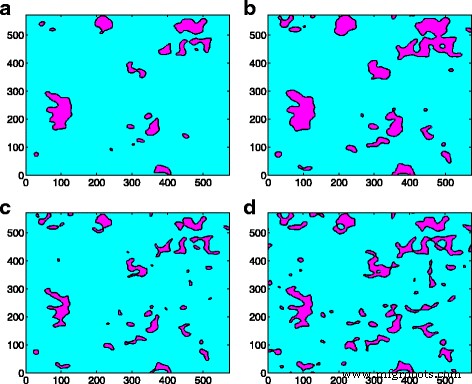
De clusterdistributiecontour (in σ ) op verschillende contactgebieden voor respectievelijk het asperity-model en het GFMD-model. een Asperity-model met 5% contactoppervlak. b Asperity-model met 10% contactoppervlak. c GFMD-model met 5% contactoppervlak. d GFMD-model met 10% contactoppervlak

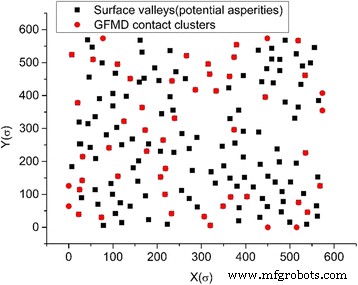
De locaties van de contactclusters en de oppervlaktedalen op 10% contactoppervlak

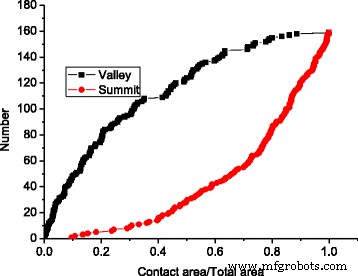
Het aantal valleien en de top aan de oppervlakte groeit in verschillende gebieden

Contactgebied-belastingsrelatie

De kracht-oppervlakverhouding onder normale belasting is essentieel voor het contactgedrag. In de eerdere modellen worden oneffenheden meestal als bolvormig en elliptisch beschouwd. Echte contactclusters zijn echter veel gecompliceerder. In deze sectie hebben we de relatie tussen contactkracht en oppervlakte van drie modellen vergeleken:(1) het GFMD-model; (2) het oneffenheidsmodel (gemarkeerd als AM), waarbij de ruwheid direct van het oppervlak wordt gehaald voordat we GFMD gebruiken om die oneffenheden in het platte elastische oppervlak te duwen (dit zorgt ervoor dat er geen onverwachte contactclustervorming is tijdens het contact); en (3) het model van Greenwood en Williamson (gemarkeerd als G-W), waarin de scherpte wordt omgezet in de equivalente bol. De bolstraal wordt verkregen door

$$ \frac{1}{R}=\frac{8}{3}{\left(\frac{m_4}{\pi}\right)}^{1/2} $$ (6)

Voor het GFMD-model en het asperity-model met oneffenheden die exact van het oppervlak zijn geëxtraheerd, kunnen de totale krachten in de interface worden verkregen door de krachten van elk contactcluster op te tellen die zijn geëxtraheerd uit GFMD. Voor het Greenwood- en Williamson-model gebruiken we de Hertz-theorie voor elke asperity-kracht (met dezelfde materiaaleigenschap die wordt gebruikt in het GFMD-model), wat betekent dat de totale kracht F kan worden uitgedrukt als

$$ F=\sum \limits_{i=1}^n{f}_i=\sum \limits_{i=1}^{\mathrm{N}}\frac{4}{3}{E}^{ \ast }{R}^{1/2}{\left(d-{z}_i\right)}^{3/2} $$ (7)

waar Z _ik is de oneffenheidshoogte, d is de verplaatsing toegepast op het stijve oppervlak, en f is de contactkracht op basis van de Hertz-contacttheorie.

In Fig. 9 vergeleken we de kracht-gebiedrelaties van de drie modellen, die lineaire relaties vertonen. Er wordt waargenomen dat de totale kracht in GFMD veel kleiner is dan die van het asperity-model en het G-W-model. F in het asperity-model is 1,80 keer dan voorspeld door GFMD, en F in het G-W-model is 1,54 keer dan voorspeld door GFMD. Dit kan worden verklaard door de RMS-helling van de contactclusters. Het is bekend dat de normale belasting evenredig is met de RMS-helling, dat wil zeggen \( L\propto \sqrt{M_2} \). In het GFMD-model bestaat het contactgebied uit een groter aantal clusters, waarvan de penetraties ondieper zijn dan die van het asperity-model. Omdat de helling van de asperity-tip kleiner is, is de RMS-helling voor het contactcluster in het GFMD-model ook kleiner. Afbeelding 10 toont de RMS-hellingen van het contactcluster voor de drie modellen. Het is te zien dat de RMS-helling van de contactclusters in GFMD kleiner is dan die van de RMS-helling van het oppervlak van 0,077, terwijl de RMS-hellingen van de beide andere twee modellen groter zijn dan die van de RMS-helling aan het oppervlak.

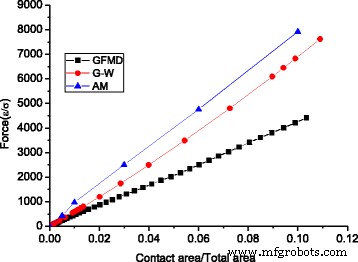
Relatie van het contactoppervlak en de belasting voor verschillende modellen

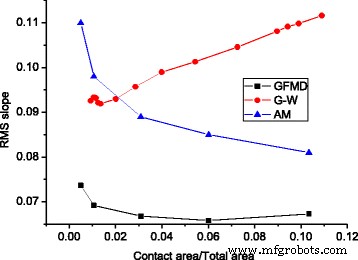
De RMS-helling van de contactclusters met verschillende contactgebieden voor verschillende modellen, waarbij de RMS-helling van het oppervlak 0,077 is

Conclusies

Om de evolutie van het contactgebied van atomaire schaal naar macroscopische schaal te vinden, is het ruwe fractale oppervlakcontactprobleem bestudeerd met behulp van het GFMD-model. We definieerden het atomaire contact door het bestaan ​​van een kracht groter dan nul en bestudeerden drie verschillende lengteschalen in hetzelfde systeem. Het blijkt dat de inter-asperity-interactie essentieel is voor de vorming van een contactcluster. Sommige clusters zijn zo dichtbij dat ze kunnen samensmelten tot een grote. Het werkelijke contactgebied is veel gecompliceerder dan voorspeld door de oppervlaktegeometrie als gevolg van elastische vervorming in het elastische gladde oppervlak. De meeste contactclusterlocaties vallen samen met de toppen/dalen aan de oppervlakte. De grootte van het cluster is echter kleiner en de vorming ervan wordt niet bepaald door de oneffenheden van het oppervlak. Naarmate het contactoppervlak groter wordt, kunnen zowel toppen als dalen zich als contactclusters vormen. In het GFMD-model is de kracht veel kleiner dan die van het asperity-model, terwijl het contactclusternummer in het GFMD-model veel groter is. De RMS-helling van de contactclusters in het GFMD-model is kleiner dan die van het asperity-model, wat verklaart waarom het asperity-model tot hogere druk leidt. Onze bevindingen suggereren dat het werkelijke contactoppervlak niet eenvoudig kan worden voorspeld door de oppervlaktegeometrie. Het daadwerkelijke contactoppervlak met de normale belasting is van belang voor het volgende onderzoek naar wrijving.