Interactie-effecten bij de assemblage van magnetische nanodeeltjes

Numerieke simulatie

Niet-interagerende nanodeeltjes

Het is leerzaam om eerst te herinneren aan het gedrag van een verzameling niet-interagerende superparamagnetische nanodeeltjes in een wisselend magnetisch veld. Het maakt het mogelijk om duidelijk de invloed van de magneto-dipoolinteractie op de assemblage-eigenschappen te zien. Gebaseerd op de Fokker-Planck-vergelijking afgeleid door W.F. Brown [39], kan men een benaderende kinetische vergelijking [10] krijgen voor de populatieaantallen n ₁ (t ) en n ₂ (t ) van twee potentiële bronnen van uniaxiale superparamagnetische nanodeeltjes

Hier, τ ₁ (T ) en τ ₂ (T ) zijn de corresponderende relaxatietijden bij een gegeven temperatuur T voor respectievelijk de eerste en tweede potentiële putten. De ontspanningstijden τ ₁ (T ) en τ ₂ (T ) hangen in wezen af ​​van de amplitude en richting van het aangelegde magnetische veld met betrekking tot de gemakkelijke anisotropie-as van de deeltjes (zie bijlage in ref. [10]). De iteratieprocedure kan worden gebruikt om het aantal putpopulaties n . te berekenen ₁ (t ) en n ₂ (t ) gedurende meerdere perioden van het wisselende magnetische veld. Het is voldoende om een ​​stationaire hysteresislus van een deeltje in een wisselend magnetisch veld te verkrijgen. Om dit te doen, kan men een benaderende relatie gebruiken voor de component van de verminderde deeltjesmagnetisatie langs de magnetische veldrichting

Hier, θ ₀ is de hoek van het externe magnetische veld ten opzichte van de as van de gemakkelijke anisotropie van het deeltje, θ _min,1 en θ _min,2 zijn de locaties van de potentiaalputminima als de functies van het verminderde aangelegde magnetische veld, h _e (t ) = H ₀ sin(ωt )/H _een , waar ω = 2πf is de hoekfrequentie, H _een zijnde het deeltje anisotropie veld. Om een ​​hysteresislus te krijgen van een verzameling willekeurig georiënteerde onafhankelijke nanodeeltjes, is het noodzakelijk om de verminderde magnetisatie m te middelen _h (t ) over de magnetische veldrichtingen. Het is vermeldenswaard dat de nauwkeurigheid van een benaderende analytische oplossing, Vgl. (1), (2) van de Fokker-Planck-vergelijking is gevalideerd [10] door middel van directe vergelijking met de numerieke oplossingen van de stochastische Landau-Lifshitz-vergelijking voor niet-interagerende magnetische nanodeeltjes.

Nanodeeltjesclusters

Om het effect van magneto-dipoolinteractie op de specifieke absorptiesnelheid van een assemblage van op elkaar inwerkende magnetische nanodeeltjes in een wisselend magnetisch veld te onderzoeken, bestuderen we in dit artikel het gedrag van een verdunde assemblage van gebruikelijke 3D-clusters van superparamagnetische nanodeeltjes en dat van fractale clusters [8, 9] die meestal ontstaan ​​in biologische media die zijn geladen met fijne magnetische nanodeeltjes.

Een quasi-bolvormige 3D-cluster van nanodeeltjes schematisch weergegeven in Fig. 1a kan worden gekenmerkt door zijn straal R _cl , en het aantal nanodeeltjes, N _p >> 1, binnen zijn volume. Aangenomen wordt dat de nanodeeltjes bijna dezelfde diameter hebben D , en hun centra, {r _ik }, ik = 1, 2,.. N _p , zijn willekeurig verdeeld in het clustervolume. We nemen ook aan dat de deeltjes zijn bedekt met dunne niet-magnetische schillen, zodat de uitwisselingsinteractie tussen de naburige nanodeeltjes van het cluster afwezig is. Zoals we hierboven vermeldden, wordt een dergelijke 3D-cluster gekenmerkt door de pakkingsdichtheid van nanodeeltjes η = N _p V /V _cl . Dit is een totaal volume van het magnetische materiaal dat is verdeeld in het volume van het cluster. Men kan de gemiddelde afstand tussen de nanodeeltjes van het cluster bepalen door middel van de relatie D _av = (6V _cl /πN _p ) ^1/3 . Vervolgens wordt de pakkingsdichtheid van nanodeeltjes gegeven door η = (D /D _av ) ³ .

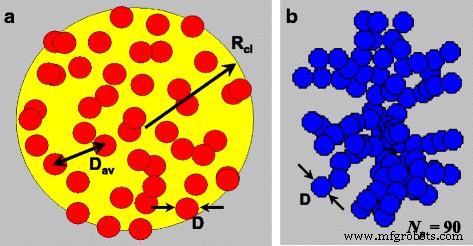
Geometrie van quasi-sferische willekeurige 3D-cluster van nanodeeltjes met één domein (a ) en fractal cluster (b ) met fractale descriptoren D _f = 2.1 en k _f = 1.3

Voor een assemblage van volledig willekeurige 3D-clusters, de oriëntaties van de gemakkelijke anisotropie-assen van nanodeeltjes {e _ik }, ik = 1, 2, .. N _p , worden willekeurig en onafhankelijk gekozen op de eenheidsbol. Als alternatief kan men aannemen dat tijdens de vorming van clusters in een oplossing onder invloed van magneto-statische interactie, er een zekere correlatie optreedt in de verdeling van de gemakkelijke anisotropie-asrichtingen van nanodeeltjes. Een mogelijkheid om dergelijke gedeeltelijk geordende clusters te beschrijven is om aan te nemen dat de gemakkelijke anisotropie-assen van de nanodeeltjes uniform zijn verdeeld in een ruimtehoek, θ < θ _max , in de bolcoördinaten.

Willekeurige 3D-clusters met een bepaald aantal deeltjes N _p van diameter D zijn in dit onderzoek als volgt gemaakt. Ten eerste hebben we een voldoende dichte en ongeveer uniforme set van N . gegenereerd willekeurige punten {ρ _ik } binnen een bolvormig volume van de straal R _cl , zodat |ρ _ik | ≤ R _cl voor alle gegenereerde punten, i = 1, 2... N , N>> N _p . Het centrum van het eerste nanodeeltje werd geplaatst in het eerste willekeurige punt, r ₁ = ρ ₁ . Dan, alle willekeurige punten met coördinaten |ρ _ik –r ₁ | ≤ D werden verwijderd uit de eerste reeks willekeurige punten. Na deze bewerking kan elk punt in de resterende reeks willekeurige punten worden gebruikt als middelpunt van het tweede nanodeeltje. Men kan bijvoorbeeld eenvoudig r . zetten ₂ = ρ ₂ . Bij de volgende stap verwijdert men alle willekeurige punten waarvan de coördinaten voldoen aan de ongelijkheid |ρ _ik –r ₂ | ≤ D . Deze procedure wordt herhaald totdat alle N _p nanodeeltjescentra worden binnen het clustervolume geplaatst. Als gevolg hiervan liggen alle willekeurige nanodeeltjescentra binnen een bol met straal R _cl , zodat |r _ik | ≤ R _cl , ik = 1, 2,... N _p . Bovendien staat geen van de nanodeeltjes in direct contact met de naburige nanodeeltjes. Dit algoritme maakt het mogelijk om willekeurige quasi-sferische 3D-clusters van magnetische nanodeeltjes te construeren voor gematigde waarden van de volumefractie van nanodeeltjes η < 0.5.

Voor een bepaalde set initiële parameters, d.w.z. D , R _cl , en N _p , verschillende willekeurige 3D-clusters verschillen door de sets van de coördinaten van de nanodeeltjescentra {r _ik } en oriëntaties {e _ik } van de eenvoudige anisotropie-assen van het deeltje. De berekeningen laten echter zien dat in de limiet N _p >> 1, de hysteresislussen die zijn verkregen voor verschillende realisaties van willekeurige variabelen {r _ik } en {e _ik } verschillen slechts in geringe mate van elkaar. Om het gedrag van een verdunde assemblage van willekeurige nanodeeltjesclusters te karakteriseren, is het noodzakelijk om de assemblagehysteresislus te berekenen die gemiddeld is over een voldoende groot aantal willekeurige clusterrealisaties. Het blijkt dat in de limiet N _p >> 1, de gemiddelde hysteresislus van clusterassemblage heeft een vrij kleine spreiding, zelfs als deze wordt gemiddeld over 20-30 onafhankelijke realisaties van willekeurige clusters met de vaste waarden van de initiële parameters D , R _cl , en N _p .

De geometrie van fractale clusters van nanodeeltjes met een enkel domein wordt gekenmerkt [42, 43] door de fractale descriptoren D _f en k _f . Per definitie is het totale aantal nanodeeltjes N _p in het fractal cluster wordt gegeven door de relatie \( {N}_p={k}_f{\left(2{R}_g/D\right)}^{D_f} \), waarbij D _f is de fractale dimensie, k _f is de fractale prefactor, en R _g zijnde de omloopstraal. Het wordt gedefinieerd [43] via het gemiddelde kwadraat van de afstanden tussen de deeltjescentra en het geometrische zwaartepunt van het aggregaat. In dit artikel werden de fractalclusters met verschillende fractaldescriptoren gemaakt met behulp van het bekende Filippov et al.'s algoritme [43]. Als voorbeeld toont Fig. 1b de geometrische structuur van fractal cluster met fractal descriptors D _f = 2.1 en k _f = 1.3 bestaande uit N _p = 90 nanodeeltjes met één domein. Geometrisch gezien lijkt het belangrijkste verschil tussen 3D- en fractale clusters te zijn dat in het laatste geval elk nanodeeltje ten minste één buur heeft die zich op de kortst mogelijke afstand tussen de nanodeeltjescentra bevindt die gelijk is aan de nanodeeltjesdiameter D .

Dynamiek van eenheidsmagnetisatievector \( {\overrightarrow{\alpha}}_i \) van i -de enkel-domein nanodeeltje van de cluster wordt bepaald door de stochastische Landau-Lifshitz (LL) vergelijking

waar γ is de gyromagnetische verhouding, κ is een fenomenologische dempingsparameter, γ ₁ = γ /(1+κ ² ), \( {\overrightarrow{H}}_{ef,i} \) is het effectieve magnetische veld en \( {\overrightarrow{H}}_{th,i} \) is het thermische veld. Het effectieve magnetische veld dat inwerkt op een afzonderlijk nanodeeltje kan worden berekend als een afgeleide van de totale clusterenergie

De totale magnetische energie van het cluster W = W _een + W _Z + W _m is een som van de magnetokristallijne anisotropie-energie W _een , Zeeman energie W _Z van de deeltjes in het aangelegde magnetische veld \( {\overrightarrow{H}}_0\sin \left(\omega t\right) \), en de energie van de onderlinge magneto-dipoolinteractie van de deeltjes W _m .

Voor nanodeeltjes met een bijna bolvorm met een uniaxiaal type magnetische anisotropie wordt de magnetokristallijne anisotropie-energie gegeven door

waar e _ik is de oriëntatie van de gemakkelijke anisotropie-as van i -de deeltje van het cluster. Zeeman energie W _Z van het cluster in aangelegd magnetisch veld wordt gegeven door

Vervolgens kan voor sferische uniform gemagnetiseerde nanodeeltjes de magnetostatische energie van het cluster worden weergegeven als de energie van de puntinteragerende dipolen die zich in de deeltjescentra r bevinden _ik binnen het cluster. Dan is de magneto-dipool-interagerende energie

waar n _ij is de eenheidsvector langs de lijn die de middelpunten van i . verbindt -th en j -de deeltjes, respectievelijk.

Dus het effectieve magnetische veld dat inwerkt op de i -de nanodeeltje van het cluster wordt gegeven door

waar H _een = 2 K /M _s. is het deeltjesanisotropieveld.

De thermische velden, \( {\overrightarrow{H}}_{th,i} \), i = 1, 2...N _p , die inwerken op verschillende nanodeeltjes van het cluster zijn statistisch onafhankelijk, met de volgende statistische eigenschappen [39] van hun componenten voor elk nanodeeltje

Hier, k _B is de Boltzmann-constante, δ _αβ is het Kroneker-symbool, en δ (t ) is de delta-functie.

De procedure voor het oplossen van stochastische differentiële vergelijkingen. (3), (8) en (9) worden in detail beschreven in Refs. [13, 40, 41].

Resultaten en discussie

Niet-interagerende ijzeroxide-nanodeeltjes

Beschouw een verdunde samenstelling van superparamagnetische nanodeeltjes met een gemiddelde diameter D . De deeltjes worden verondersteld dicht opeengepakt te zijn in een omringend medium, en hun gemakkelijke anisotropie-assen zijn willekeurig in de ruimte georiënteerd. De hysteresislus van een dergelijk samenstel in een wisselend magnetisch veld H = H ₀ sin(ωt ) kan worden berekend [10] met Vgl. (1) en (2). Deze benadering maakt het vanwege zijn eenvoud mogelijk om gedetailleerde berekeningen uit te voeren van de hysteresislussen van de assemblage voor verschillende deeltjesgroottes, afhankelijk van de frequentie en amplitude van het wisselende magnetische veld. In de uitgevoerde berekeningen, in overeenstemming met de experimentele gegevens [2,3,4,5,6], wordt aangenomen dat de verzadigingsmagnetisatie van ijzeroxide nanodeeltjes M is _s. = 70 Am ² /kg, waarbij de magnetische anisotropieconstante K . is = 10 ⁴ J/m ³ . De montagetemperatuur is T = 300 K, en de diameters van nanodeeltjes liggen in het bereik D =10–30 nm. Deze parameters lijken typerend voor experimenten met nanodeeltjes van ijzeroxide.

Figuur 2 toont de SAR van niet-interagerende assemblages van ijzeroxide nanodeeltjes bij verschillende frequenties bij een vaste amplitude van wisselend magnetisch veld, H ₀ = 8 kA/m. Zoals te zien is, geldt voor het frequentiebereik dat kenmerkend is voor magnetische hyperthermie f = 200-500 kHz, SAR heeft een maximum voor de assemblage van ijzeroxide-nanodeeltjes met een diameter van D =20-21 nm. Het is opmerkelijk dat zelfs bij een relatief matige amplitude van een wisselend magnetisch veld, de SAR van de assemblage voldoende hoge waarden bereikt, 350-450 kW/kg, als de diameters van nanodeeltjes correct worden gekozen.

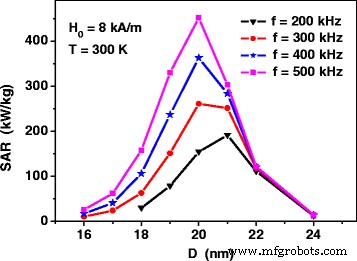
De specifieke absorptiesnelheid van niet-interagerende assemblage van nanodeeltjes van ijzeroxide, verkregen door middel van Vgl. (1) en (2), als functie van de gemiddelde deeltjesdiameter bij verschillende frequenties van het wisselende magnetische veld

De experimenteel gemeten SAR-waarden voor samenstellingen van nanodeeltjes van ijzeroxide liggen echter in de regel aanzienlijk lager [18,19,20,21] deze theoretische waarden. Zoals we in de volgende paragraaf zullen zien, kan dit feit worden verklaard [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] door de invloed van sterke magneto-dipoolinteractie in dichte samenstellingen van magnetische nanodeeltjes.

Montage van 3D-clusters

Beschouw nu de hysteresislussen van een verdunde verzameling van willekeurige 3D-clusters met gemakkelijke anisotropie-assen van individuele nanodeeltjes die willekeurig in de ruimte zijn georiënteerd. Zoals figuur 2 laat zien, komt voor de assemblage van niet-interagerende ijzeroxide-nanodeeltjes de piek van de energieabsorptie in een wisselend magnetisch veld overeen met deeltjes met een diameter D = 20 nm. Daarom hebben we eerst de hysteresislussen berekend van een verzameling 3D-clusters met deeltjesdiameter D = 20 nm.

Figuur 3a toont de evolutie van de hysteresislussen van de assemblage, afhankelijk van de gemiddelde afstand tussen de nanodeeltjescentra D _av op de vaste waarde van de deeltjesdiameter D . De frequentie en amplitude van het wisselende magnetische veld zijn vastgesteld op f = 400 kHz en H ₀ =8 kA/m, respectievelijk. Het aantal deeltjes in de clusters is gelijk aan N _p = 40. De berekeningen worden uitgevoerd op T = 300 K, en de magnetische dempingsconstante wordt aangenomen als κ = 0.5.

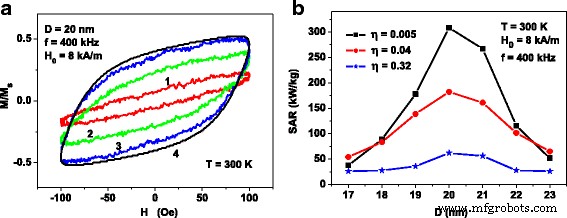
(een ) Evolutie van de hysteresislussen van verdunde assemblage van clusters van ijzeroxide-nanodeeltjes met een diameter D = 20 nm voor verschillende verhoudingen D _av /D :(1 ) D _av /D =1.46; (2 ) D _av /D =2,92; (3 ) D _av /D = 5.84. Hysteresislus 4 komt overeen met assemblage van niet-interagerende nanodeeltjes van dezelfde diameter. Het wordt berekend door middel van Vgl. (1) en (2). (b ) SAR als functie van de gemiddelde nanodeeltjesdiameter D voor verdunde samenstellingen van clusters van nanodeeltjes met verschillende pakkingsdichtheid η

Het is duidelijk dat de afname van de gemiddelde afstand tussen de nanodeeltjes van het cluster leidt tot een toename van de intensiteit van de magneto-dipoolinteractie binnen het cluster. Merk op dat voor N _p = 40, de verhoudingen D _av /D gespecificeerd in Fig. 3a komen overeen met de clusterpakkingsdichtheden η =0,005, 0,04 en 0,32 dienovereenkomstig. In Fig. 3a kan men zien dat het hysteresislusoppervlak snel afneemt als functie van de parameter η . Ter vergelijking toont Fig. 3a ook de hysteresislus 4, berekend voor een samenstel van niet-interagerende deeltjes, d.w.z. in de limiet D _av /D → ∞, N _p = const, met behulp van vergelijkingen. (1) en (2).

Men kan zien dat de hysteresislus 3 (η =0,005) in Fig. 3a blijkt dicht bij de hysteresislus van de assemblage van niet-interagerende nanodeeltjes te zijn. Daarom, in het geval η ≤ 0,005 de magneto-dipoolinteractie van de nanodeeltjes in het cluster kan worden verwaarloosd. Echter, voor η ≥ 0,04 de magneto-dipoolinteractie heeft een significante invloed op de eigenschappen van een verzameling willekeurige 3D-clusters. Een gelijkaardige evolutie van de hysteresislussen van de assemblage werd ook verkregen voor de frequenties f =respectievelijk 300 en 500 kHz.

De hysteresislussen getoond in Fig. 3a worden berekend voor verschillende verhoudingen D _av /D , maar voor het vaste aantal nanodeeltjes in de cluster N _p =40. De gedetailleerde computersimulaties laten echter zien dat de vorm van de hysteresislus van een verdunde verzameling willekeurige 3D-clusters praktisch onveranderd is, als het aantal deeltjes, N _p >> 1, en de straal van het cluster R _cl zijn gewijzigd zodat de pakkingsdichtheid van nanodeeltjes η blijft constant. Daarom hangt de hysteresislus van verdunde assemblage van willekeurige 3D-clusters voornamelijk af van de clusterpakkingsdichtheid η .

Figuur 3b toont de SAR van assemblages van willekeurige clusters van ijzeroxide-nanodeeltjes voor verschillende η waarden. De SAR van de assembly wordt berekend [10] als SAR = M _s fA /ρ , waar A is het hysteresislusgebied in de variabelen (M /M _s. , H ), ρ zijnde de dichtheid van ijzeroxide nanodeeltjes waarvan wordt aangenomen dat het ρ . is = 5 × 10 ³ kg/m ³ . Zoals figuur 3b laat zien, neemt de SAR af als functie van η als gevolg van een toename van de intensiteit van de magneto-dipoolinteractie binnen de clusters. Tegelijkertijd blijft de afhankelijkheid van de assemblage SAR van de gemiddelde deeltjesdiameter bestaan, hoewel deze minder uitgesproken wordt.

Voor kleine waarden van η ≤ 0,005, de SAR van willekeurige assemblage van 3D-clusters valt eigenlijk samen met die voor een assemblage van niet-interagerende nanodeeltjes, weergegeven in Fig. 2. Aan de andere kant daalt SAR ongeveer zes keer wanneer de clusterpakkingsdichtheid toeneemt tot η = 0.32. Dan komt het in de buurt van typische SAR-waarden ~ 50-100 kW/kg, die zijn verkregen in een aantal experimenten [5, 18,19,20,21] met ijzeroxide-nanodeeltjes.

Assemblage van fractalclusters

Soortgelijke berekeningen werden uitgevoerd voor verdunde samenstellingen van fractale clusters van nanodeeltjes met verschillende fractale descriptoren. Zoals figuur 4 laat zien, neemt voor fractale clusters van nanodeeltjes ook de SAR als functie van de deeltjesdiameter aanzienlijk af ten opzichte van die van de assemblage van niet-interagerende nanodeeltjes. In tegenstelling tot de assemblage van 3D-clusters worden de piekwaarden van SAR echter systematisch verschoven naar kleinere deeltjesdiameters, behalve in het geval van fractale dimensie D _f = 2.7, wat dicht in de buurt komt van het geval van 3D-clusters met D _f = 3.0. Het is ook interessant om op te merken dat voor niet-optimale nanodeeltjesdiameters, bijvoorbeeld voor nanodeeltjes met diameters D ≤ 17 nm, de invloed van magneto-dipoolinteractie leidt tot verhoging van de SAR ten opzichte van het geval van assemblage van niet-interagerende nanodeeltjes, aangezien de SAR van de assemblage van niet-interagerende nanodeeltjes erg klein is voor nanodeeltjes met diameters D ≤ 17 nm.

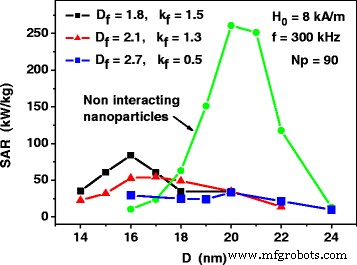
SAR als functie van de gemiddelde nanodeeltjesdiameter D voor verdunde assemblages van fractale clusters van nanodeeltjes met verschillende fractale descriptoren. De SAR van de assemblage van niet-interagerende nanodeeltjes wordt berekend door middel van Vgl. (1) en (2)

De berekeningen getoond in Fig. 4 werden uitgevoerd in de veronderstelling dat er dunne niet-magnetische schillen met een dikte t bestaan. _Sh =1 nm aan het oppervlak van magnetische nanodeeltjes. Dit voorkomt dat de nanodeeltjes van het fractale cluster een directe uitwisselingsinteractie hebben. Het is duidelijk dat de toename van de niet-magnetische schaaldikte de intensiteit van de magneto-dipoolinteractie van de dichtstbijzijnde nanodeeltjes vermindert, naarmate de gemiddelde afstand tussen de magnetische kernen op de nanodeeltjes toeneemt. Figuur 5 laat zien dat de toename van de niet-magnetische schaaldikte een goede manier is om de SAR van de assemblage van fractale clusters van nanodeeltjes te verhogen. Namely, for sufficiently large thickness of non-magnetic shells the dependence of the SAR on the particle diameter resembles that for weakly interacting magnetic nanoparticles. This fact may be important for the application of magnetic nanoparticle assemblies in magnetic hyperthermia.

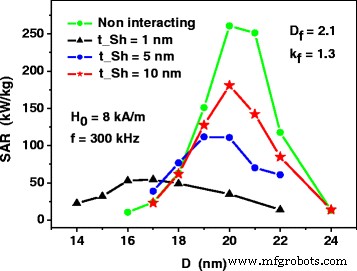
The dependence of the SAR of dilute assembly of fractal clusters on the thickness t _Sh of the non-magnetic shells at the surface of the nanoparticles. The SAR of the assembly of non-interacting nanoparticles is calculated by means of Eqs. (1) and (2)

Conclusies

The main conclusion of this study is that the SAR of a dilute assembly of clusters of magnetic nanoparticles in alternating magnetic field is significantly reduced with increasing of the intensity of magneto-dipole interaction in the clusters. For usual 3D clusters of nanoparticles, the intensity of the magneto-dipole interaction can be characterized by dimensionless packing density, η  = N _p V /V _cl  = (D /D _av ) ³ . The latter determines the average distance between the nanoparticles of the cluster. The calculations show that for the assembly of random 3D clusters, the energy absorption peak, which for iron oxide nanoparticles corresponds to particles with average diameter D  = 20 nm, is reduced about six times when the packing density increases from η  = 0.005 up to η  = 0.32. The dependence of the assembly SAR on the mean nanoparticle diameter is retained with increase of η , but becomes less pronounced.

For dilute assemblies of fractal clusters of magnetic nanoparticles, the SAR values also decrease several times irrespective on the fractal descriptors of the assembly. In addition, the peak values of SAR are shifted systematically to smaller particle diameters, as a rule. It is important to note, however, that the increase of the non-magnetic shell thickness at the nanoparticle surfaces restores the SAR values close to that of the assembly of weakly interacting nanoparticles. This fact can be important for various biomedical applications of magnetic nanoparticle assemblies.

The model considered in this paper takes into account the geometrical structure of nanoparticle assemblies observed experimentally in biological media [4, 8, 9] (in particular in tumors), i.e., the agglomeration of nanoparticles in a sufficiently dense fractal clusters of different sizes, with different numbers of nanoparticles in the clusters. The stochastic LL Eq. (3) accurately describes the real dynamics of the magnetic moments of nanoparticles taking into account both the magneto-dipole interaction between the particles and the effect of thermal fluctuations. The cluster model studied allows obvious generalization that can make it more practical. First, it is necessary to take into account the size distribution of magnetic nanoparticles in the assembly. Second, in some cases exchange interaction may exist between neighboring nanoparticles of the cluster if they are in direct atomic contact.

The theoretical results obtained in this study seem to be in a satisfactory agreement with recent experimental data [35] for iron oxide nanoparticles of optimal diameters. Indeed, according to Ref. [35], the SAR of the iron oxide nanoparticles increases with the average diameter of the nanoparticles and peaks for nanoparticles with mean diameter D  = 20–21 nm. In addition, the SAR decreases [35] with a decrease in the average distance between the nanoparticles due to increasing intensity of the magneto-dipole interaction.

Unfortunately, in some experimental studies [5, 21] carried out to optimize the properties of magnetic nanoparticles for use in magnetic hyperthermia, often do not take into account the theoretical predictions [10, 11] about significant dependence of the assembly SAR on the characteristic size of the magnetic nanoparticles. As shown in this paper, this dependence can be substantial even for rather dense nanoparticle assemblies. From a theoretical point of view, it is obvious [10] that the assembly of iron oxide nanoparticles with very small, D  ≤ 10 nm, or too big, D  ≥ 30 nm diameters can hardly provide a sufficiently high SAR values for typical for magnetic hyperthermia frequencies, f  = 200–600 kHz, and magnetic field amplitudes H ₀  ~ 8 kA/m. The creation of mono-crystalline iron oxide nanoparticles with sharp size distribution near the optimal diameter has to be promising for application in magnetic hyperthermia.