Effecten van grootte en aggregatie/agglomeratie van nanodeeltjes op de grensvlak-/interfase-eigenschappen en treksterkte van polymeernanocomposieten

Abstract

In deze studie worden verschillende eenvoudige vergelijkingen voorgesteld om de effecten van grootte en dichtheid op het aantal, het oppervlak, de verstijvingsefficiëntie en het specifieke oppervlak van nanodeeltjes in polymeer nanocomposieten te onderzoeken. Bovendien worden de rollen van nanodeeltjesgrootte en interfasedikte in de grensvlak-/interfase-eigenschappen en treksterkte van nanocomposieten verklaard door verschillende vergelijkingen. De aggregaten/agglomeraten van nanodeeltjes worden ook aangenomen als grote deeltjes in nanocomposieten, en hun invloeden op de eigenschappen van nanodeeltjes, interface/interfase-eigenschappen en treksterkte worden besproken. De kleine omvang heeft een gunstige invloed op het aantal, het oppervlak, de verstijvingsefficiëntie en het specifieke oppervlak van nanodeeltjes. Slechts 2 g geïsoleerde en goed verspreide nanodeeltjes met een straal van 10 nm (R = 10 nm) en een dichtheid van 2 g/cm³ produceer het aanzienlijke grensvlak van 250 m² met polymeermatrix. Bovendien kan alleen een dikke interfase geen hoge grensvlak-/interfaseparameters en significante mechanische eigenschappen in nanocomposieten produceren, omdat de vulstofgrootte en aggregaten/agglomeraten deze termen ook beheersen. Het blijkt dat een dikke interfase (t = 25 nm) rond de grote nanodeeltjes (R = 50 nm) verbetert alleen de B interfase-parameter tot ongeveer 4, terwijl B = 13 wordt verkregen door de kleinste nanodeeltjes en de dikste interfase.

Achtergrond

De nanocomposieten vertonen substantiële eigenschappen door slechts een klein gehalte aan nanovulstof [1,2,3,4,5]. De belangrijke eigenschappen van polymere nanocomposieten zorgen voor een breed scala aan toepassingen in verschillende technologieën, zoals geavanceerde materialen en goederen, medicijnen, energieapparaten en sensoren [6]. De onderzoeken naar verschillende soorten polymere nanocomposieten zijn gericht op het verkrijgen van hoogwaardige producten door een eenvoudig fabricageproces en lage kosten.

De aanzienlijke eigenschappen van polymere nanocomposieten worden toegeschreven aan goede grensvlakeigenschappen tussen polymeermatrix en nanodeeltjes zoals grensvlak en interactie/adhesie aan grensvlak [7,8,9,10,11,12,13]. De hoge niveaus van grensvlakeigenschappen leiden tot de vorming van een andere fase als interfase rond de nanodeeltjes die verschilt van zowel de polymeermatrix als nanodeeltjes, wat het voordeel van nanocomposieten ten opzichte van conventionele microcomposieten laat zien [14,15,16,17,18]. Veel theoretische onderzoeken naar grensvlak-/interfase-eigenschappen hebben een grote hoeveelheid informatie opgeleverd om de gewenste eigenschappen te verkrijgen. Het grote oppervlak van nanodeeltjes en de sterke aantrekkelijke interactie tussen deeltjes resulteren echter in de aggregatie/agglomeratie [19, 20]. De sterke en dichte collectieven van nanodeeltjes duiden de aggregatie aan, maar de losjes verbonden deeltjes tonen de agglomeratie die kan worden verbroken door mechanische spanning [21].

De aggregatie / agglomeratie van nanodeeltjes vermindert de potentiële verbetering van mechanische eigenschappen in nanocomposieten, vanwege de beperking van het grensvlakgebied [22, 23]. Daarom is de belangrijkste uitdaging bij de productie van nanocomposieten het bereiken van kleine nanodeeltjes en een goede dispersie van nanodeeltjes. Het is van vitaal belang om de aantrekkingskracht tussen nanodeeltjes die de aggregatie/agglomeratie veroorzaken te overwinnen, in plaats van de structuur van nanodeeltjes te verstoren. Verrassend genoeg hebben Dorigato et al. [24] suggereerde een model dat aantoont dat de primaire vulstofaggregatie de polymere nanocomposieten versterkt, terwijl de geagglomereerde nanodeeltjes gewoonlijk negatieve effecten hebben op de mechanische prestaties van polymere nanocomposieten [21, 25]. Dienovereenkomstig is het onderzoek naar aggregatie/agglomeratie van nanodeeltjes nodig om de werkelijke effecten op de eigenschappen van nanocomposieten te onthullen. Hoewel de nanodeeltjesgrootte wordt aangenomen als een aantrekkelijk voordeel in polymere nanocomposieten, zijn de effecten van isolatie of aggregatie/agglomeratie op de belangrijkste eigenschappen van nanodeeltjes zoals aantal, oppervlakte en specifiek oppervlak niet bestudeerd in de literatuur. Bovendien is de aggregatie/agglomeratie van nanodeeltjes aangenomen als een algemene term die het gedrag van nanocomposieten kwalitatief verandert. Ook zijn de mogelijke rollen van nanodeeltjes en interfasedimensies op de grensvlak-/interfase-eigenschappen niet beschreven in eerdere studies.

Methoden

In dit artikel worden de effecten van vulstofgrootte en dichtheid op het aantal, het oppervlak, de verstijvingsefficiëntie en het specifieke oppervlak van nanodeeltjes in polymeer nanocomposieten verklaard door de juiste vergelijkingen. Ook wordt aangenomen dat de aggregatie/agglomeratie van nanodeeltjes grote deeltjes zijn en dat hun invloeden op verschillende termen worden onthuld. Evenzo worden de mogelijke rollen van nanodeeltjes en interfasegroottes in de grensvlak-/interfaseparameters en treksterkte van nanocomposieten besproken. De belangrijkste focus van dit artikel ligt op de sferische nanodeeltjes, maar andere geometrieën van nanodeeltjes kunnen worden bestudeerd door de voorgestelde vergelijkingen te ontwikkelen.

Het aantal bolvormige geïsoleerde nanodeeltjes in een nanocomposiet kan worden berekend door het gewicht van nanodeeltjes (W _f ) als:

$$ N=\frac{W_f}{d_f\frac{4}{3}\pi {R}^3}. $$ (1)

waar d _f en R zijn respectievelijk de dichtheid en straal van nanodeeltjes. In deze toestand wordt het totale oppervlak van gedispergeerde nanodeeltjes gegeven door:

$$ A=N\links(4\pi {R}^2\rechts). $$ (2)

A kan worden beschouwd als het grensvlak tussen polymeermatrix en nanodeeltjes. Vervanging van N van vgl. 1 in Verg. 2 leidt naar:

$$ A=\frac{3{W}_f}{d_fR}. $$ (3)

die correleert met de A met W _f , d _f , en R .

Elk nanodeeltje introduceert een verstijvend effect in de polymeermatrix door mechanische betrokkenheid van polymeerketens. De mate van spanningsdeling tussen polymeermatrix en nanodeeltjes hangt af van het grensvlak en de stijfheid van nanodeeltjes. Als resultaat kan een nieuwe parameter als de verstijvingsefficiëntie van nanodeeltjes worden gedefinieerd als:

$$ SE={AE}_f=\frac{3{W}_f}{d_fR}{E}_f. $$ (4)

waar E _f is de Young's modulus van nanodeeltjes. De verstijvingsefficiëntie als functie van de eigenschappen van nanodeeltjes drukt het vermogen van nanodeeltjes voor de verstijving van nanocomposieten uit. Bovendien wordt het specifieke oppervlak van deeltjes uitgedrukt als:

$$ {A}_c=\frac{A}{m}=\frac{A}{d_fv}=\frac{4\pi {R}^2}{d_f\frac{4}{3}\pi { R}^3}=\frac{3}{d_fR}. $$ (5)

waar m en v zijn respectievelijk de totale massa en het volume van nanodeeltjes. Deze parameter drukt de oppervlakte van 1 g deeltjes uit en is dus niet afhankelijk van de concentratie van nanodeeltjes in nanocomposiet.

Nu worden de treksterkte en grensvlak-/interfase-eigenschappen gegeven door eenvoudige vergelijkingen. Pukanszky [26] suggereerde een model voor de treksterkte van composieten als functie van vulstofgehalte en grensvlak-/interfase-eigenschappen als:

$$ \sigma ={\sigma}_m\frac{1-{\varphi}_f}{1+2.5{\varphi}_f}\exp \left(B{\varphi}_f\right). $$ (6)

waar σ _m toont de treksterkte van polymeermatrix en φ _f is de volumefractie van nanofiller. Dit model werd oorspronkelijk voorgesteld voor composieten, maar dit model laat goede overeenkomsten zien met de experimentele resultaten van verschillende polymere nanocomposieten. Er wordt een goede overeenkomst verkregen tussen de experimentele gegevens van treksterkte en de voorspellingen van de Pukanszky-vergelijking in veel monsters zoals PP/SiO₂ [27], PEEK/SiO₂ [28], PVC/CaCO₃ [29], PP/CaCO₃ [30] en PVC/SiO₂ [31] de B . berekenen parameter als respectievelijk 4.12, 3.15, 3.07, 2.5 en 2.1. Deze voorbeelden valideren de toepassing van het Pukanszky-model voor de treksterkte van polymere nanocomposieten.

B is een grensvlakparameter die het niveau van grensvlakadhesie aangeeft door:

$$ B=\left(1+{A}_c{d}_ft\right)\ln \left(\frac{\sigma_i}{\sigma_m}\right). $$ (7)

waar t en σ _ik zijn respectievelijk de dikte en sterkte van de interfase.

Vervanging van A _c van vgl. 5 in de laatste vergelijking presenteert:

$$ B=\left(1+3\frac{t}{R}\right)\ln \left(\frac{\sigma_i}{\sigma_m}\right). $$ (8)

Het toepassen van de bovenstaande vergelijking in het Pukanszky-model levert de relatieve sterkte op (σ /σ _m ) als:

$$ {\sigma}_R=\frac{1-{\varphi}_f}{1+2.5{\varphi}_f}\exp \left[\left(1+3\frac{t}{R}\right )\ln \left(\frac{\sigma_i}{\sigma_m}\right){\varphi}_f\right]. $$ (9)

die de treksterkte expliciet koppelt aan vul- en interfase-eigenschappen. We moeten ook de grootte-effecten aangeven, die ongetwijfeld bestaan bij het modelleren van breuk [32,33,34].

De volumefractie van interfase (φ _ik ) voor nanocomposieten die bolvormige nanodeeltjes bevatten, kan worden overwogen [35] door:

$$ {\varphi}_i=\left[{\left(\frac{R+t}{R}\right)}^3-1\right]{\varphi}_f. $$ (10)

waarin t = 0 resulteert in φ _ik = 0 geeft de afwezigheid van interfase in nanocomposiet aan. De analytische modellen in deze studie kunnen van toepassing zijn waar andere modellen, zoals de cohesieve zone, de interfasegebieden beschrijven. Sommige eerdere studies hebben de interfase door sommige modellen overwogen, zoals 2D eindige elementen [36, 37].

In ons vorige werk [38], a interfaseparameter voor polymere nanocomposieten versterkt met sferische nanodeeltjes werd gedefinieerd als:

$$ a=10\left(\frac{t}{R}\right)\left(\frac{10{E}_i}{E_f}-1\right). $$ (11)

waar E _ik is de modulus van interfase. Deze vergelijking correleert de a aan verschillende effectieve parameters van nanofiller en interfase. een werd berekend voor sommige nanocomposieten variërend van 0,8 tot 19 [38]. Er werd gemeld dat een hoger niveau van a introduceert een betere modulus in nanocomposiet.

Resultaten en discussie

In het eerste deel van deze sectie worden de effecten van grootte en dichtheid op verschillende eigenschappen van nanodeeltjes uitgezet door contourplots en worden de resultaten besproken om de invloed van aggregatie/agglomeratie te verduidelijken. In de volgende stap worden de rollen van de straal van nanodeeltjes (inclusief de aggregatie/agglomeratie) en interfasedikte in de grensvlak-/interfase-eigenschappen en nanocomposietprestaties bestudeerd.

Figuur 1 illustreert de aggregatie/agglomeratie van nanodeeltjes in een nanocomposiet. Wanneer de geïsoleerde en verspreide nanodeeltjes zich ophopen, kan worden aangenomen dat er een groot nanodeeltje wordt gevormd. Volgens Fig. 1 indien geïsoleerde nanodeeltjes met R straalaggregaat/agglomeraat, wordt een groot deeltje geproduceerd met een hoge straal. Hierdoor kan de aggregatie/agglomeratie van nanodeeltjes fysiek worden aangenomen door groei van de deeltjesgrootte in nanocomposieten. Dit voorval beïnvloedt de kenmerken van nanodeeltjes en interfase die uiteindelijk het gedrag van nanocomposieten veranderen.

Schematische illustratie van aggregatie/agglomeratie van nanodeeltjes in polymeer nanocomposieten. Wanneer meerdere nanodeeltjes met straal R worden geaggregeerd/geagglomereerd, wordt een groot deeltje gevormd

Afbeelding 2 toont de rollen van R en d _f in ln (N) en A niveaus bij constant W _f = 2 g. Volgens figuur 2a, lage N wordt waargenomen door de hoge waarden van R en d _f , maar N neemt toe wanneer R en d _f verminderen. Dus de dichtheid en grootte van nanodeeltjes hebben een omgekeerd effect op het aantal deeltjes in polymeer nanocomposieten bij een constante vulstofconcentratie. De kleine nanodeeltjes met een lage dichtheid produceren een groot aantal nanodeeltjes in nanocomposieten, terwijl de grote en dichte nanodeeltjes weinig deeltjes maken. Dienovereenkomstig verminderen de aggregaten/agglomeraten het aantal nanodeeltjes in nanocomposieten aanzienlijk bij een constante vulstofconcentratie.

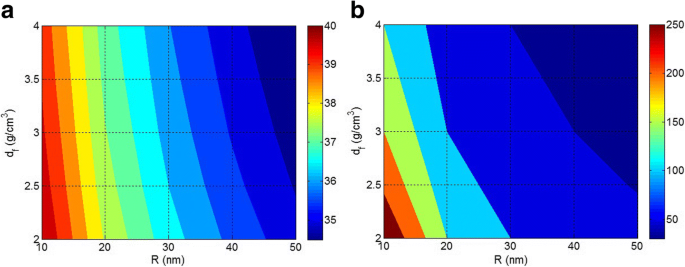
Contourplots om de rollen van R . weer te geven en d _f parameters in a ln (N ) en b A (m² ) bij W _f = 2 g

Afbeelding 2b illustreert de effecten van R en d _f parameters op het totale oppervlak van nanodeeltjes (A in m ² ) bij W _f = 2 g. Het oppervlak van nanodeeltjes wordt aangenomen als het grensvlak tussen polymeer en nanodeeltjes die de spanning overdragen van matrix naar nanodeeltjes. De spanning kan efficiënt worden getransporteerd van polymeer naar nanodeeltjes om de mechanische eigenschappen te verbeteren, wanneer het grensvlak groot genoeg is [39, 40]. Zoals te zien is in figuur 2b, wordt het grootste grensvlak bereikt door de kleinste bereiken van R en d _f . Het is ook interessant dat slechts 2 g geïsoleerde en goed verspreide nanodeeltjes met R = 10 nm en d _f = 2 g/cm³ produceer ongeveer 250 m² grensvlak met polymeermatrix. Het grensvlak wordt echter kleiner door de grootte en dichtheid van nanodeeltjes te vergroten en A onder 50 m² wordt verkregen bij R> 40 nm en d _f> 3 g/cm³ . Het significante verschil tussen de grensvlakken bij verschillende deeltjesgroottes geeft aan dat de nanodeeltjesgrootte een belangrijke parameter is in nanocomposieten. De grote nanodeeltjes veroorzaken een klein grensvlak dat het significante voordeel van nanodeeltjes in nanocomposieten verslechtert. Opgemerkt moet worden dat de vulstofconcentratie in nanocomposieten misschien niet te hoog is in vergelijking met microcomposieten, maar het buitengewone oppervlak van nanodeeltjes resulteert gewoonlijk in de interactie tussen deeltjes en aggregatie/agglomeratie. Als gevolg hiervan, hoewel de hoge gehalten aan nanodeeltjes in nanocomposieten de accumulatie versterken, vindt de aggregatie/agglomeratie van nanodeeltjes in het algemeen plaats in polymere nanocomposieten bij verschillende vulstofconcentraties die het grensvlak verkleinen en de prestaties verzwakken.

Afbeelding 3a toont de contourgrafieken van ln (SE) als functie van R en d _f bij W _f = 2 g en E _f = 100 GPa. De verstijvingsefficiëntie van nanodeeltjes neemt toe wanneer kleine nanodeeltjes met een lage dichtheid worden opgenomen in de polymeermatrix, wat aantoont dat de nanodeeltjesgrootte een effectieve rol speelt bij de verstijving van nanodeeltjes in polymeer nanocomposieten. Aan de andere kant verslechteren de geaggregeerde / geagglomereerde nanodeeltjes de prestaties van polymere nanocomposieten door de efficiëntie van nanodeeltjes te verminderen. De kleine nanodeeltjes met een lage dichtheid verhogen op significante wijze de stijfheid van nanocomposieten door de grote mate van spanningsoverdracht tussen polymeerketens en nanodeeltjes. Een eerdere studie op dit gebied heeft de fysica van de invloed van vulradius op de spanningsoverdracht van polymeermatrix naar vezel verklaard met behulp van de moleculaire dynamica-simulaties [41]. De grote en dichte deeltjes kunnen echter niet de hoge stijfheid van nanodeeltjes in de polymeermatrix introduceren, wat een composiet met een slechte stijfheid suggereert. Daarom bepalen de kenmerken van nanodeeltjes aanzienlijk de eigenschappen van nanocomposieten.

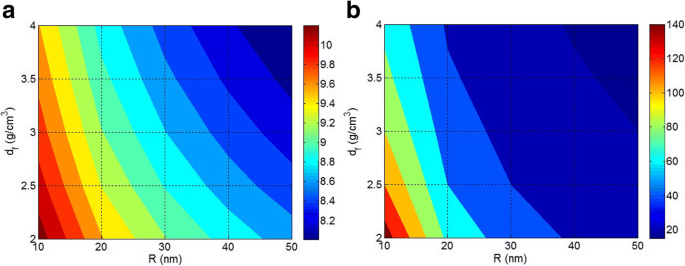
De effecten van R en d _f op een ln (SE) met ln (m² GPa) eenheid en b A _c (m² /g) bij W _f = 2 g en E _f = 100 GPa

Afbeelding 3b toont ook de niveaus van A _c parameter op verschillende R en d _f waarden bij W _f = 2 g en E _f = 100 GPa. Opgemerkt wordt dat de beste A _c wordt verkregen door kleine nanodeeltjes met een lage dichtheid, terwijl de slechtste wordt geproduceerd door grote en dichte deeltjes. De A _c waarde van ongeveer 140 m² /g wordt bereikt door R = 10 nm en d _f = 2 g/cm³ , terwijl A _c niveau van minder dan 20 m² /g wordt weergegeven door een grote deeltjesgrootte en een hoge dichtheid. Als gevolg hiervan, R en d _f parameters tonen negatieve effecten op A _c in polymeer nanocomposieten. Er wordt geconcludeerd dat A _c parameter die het grensvlak van 1 g geïsoleerde nanodeeltjes uitdrukt, geeft de beste niveaus door kleine nanodeeltjes. Als gevolg hiervan kunnen de grote nanodeeltjes of aggregaten/agglomeraten geen aanzienlijke A produceren _c die de efficiëntie van nanodeeltjes in polymeer nanocomposieten vermindert. Het is bekend dat de prestaties van nanocomposieten zoals mechanische eigenschappen, vlamvertraging en barrière-eigenschappen direct verband houden met het grensvlak tussen polymeer en nanodeeltjes [10, 42]. Een grote A _c kan acceptabele niveaus voor nanocomposieteigenschappen produceren door een kleine hoeveelheid nanodeeltjes, vanwege het grote grensvlak tussen polymeermatrix en nanodeeltjes. Dienovereenkomstig is het beheersen van de grootte en dichtheid van nanodeeltjes een uitdaging in nanocomposieten om de beste eigenschappen te creëren.

Nu worden de effecten van nanodeeltjes en interfase-afmetingen op de grensvlak-/interfase-eigenschappen en treksterkte van nanocomposieten verklaard door de voorgestelde vergelijkingen. Afbeelding 4 illustreert de effecten van R en t op B grensvlakparameter en treksterkte door Pukanszky-model (Vgl. 6) bij σ _ik /σ _m = 5 en φ _f = 0,02. Gebaseerd op Fig. 4a, de B niveau van 13 wordt verkregen door de kleinste nanodeeltjes en de dikste interfase. Ook B neemt af tot minder dan 3 wanneer de grootte van nanodeeltjes groeit tot ongeveer 40 nm en de interfasedikte afneemt tot minder dan 10 nm. Daarom spelen de afmetingen van nanodeeltjes en interfase een verschillende rol in B parameter. Ook moet worden opgemerkt dat de kleine nanodeeltjes zonder vorming van een sterke interfase geen hoge B kunnen geven in polymeer nanocomposieten. Aan de andere kant, een dikke interfase (t = 25 nm) rond de grote nanodeeltjes (R = 50 nm) verbetert alleen de B parameter tot ongeveer 4. Dientengevolge zijn zowel nanodeeltjes- als interfasedimensies belangrijk om een hoog niveau van B te verkrijgen in nanocomposieten. Bij een constant niveau van interfasedikte neemt de groei van de nanodeeltjesgrootte door aggregatie/agglomeratie echter af B parameter die de negatieve effecten van aggregaten/agglomeraten op de grensvlak-/interfase-eigenschappen aantoont.

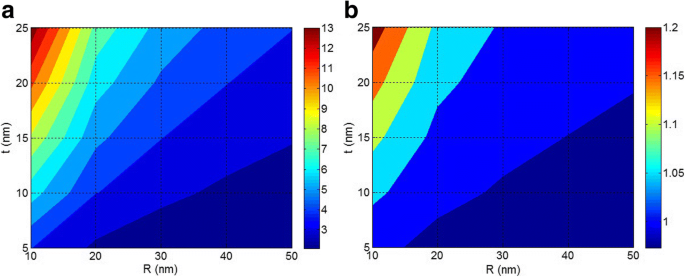
een B grensvlakparameter en b relatieve treksterkte door Pukanszky-model bij verschillende bereiken van R en d _f en constante σ _ik /σ _m = 5 en ϕ _f = 0,02

Afbeelding 4b toont ook de effecten van R en t parameters op de treksterkte van nanocomposieten door het Pukanszky-model. Er wordt waargenomen dat kleine nanodeeltjes en dikke interfase de sterkte van nanocomposieten verbeteren. Een slechte sterkte wordt echter waargenomen door grote deeltjes en dunne interfase. Daarom zijn beide R en t parameters beïnvloeden de treksterkte van nanocomposieten. Bovendien blijkt dat de sterkte van nanocomposieten afneemt als nanodeeltjes groter worden, door aggregatie/agglomeratie. Dienovereenkomstig is het essentieel om de nanodeeltjes in polymeermatrix op kleine schaal te isoleren en te dispergeren om de beste prestaties te bereiken. Aangezien nanodeeltjes van nature de neiging hebben tot aggregatie/agglomeratie, kan modificatie van hun oppervlak of functionalisering van polymeerketens de accumulatie voorkomen [19, 43, 44].

Afbeelding 5 toont de afhankelijkheden van de interfase-volumefractie (φ _ik ) en a interfase-parameter op R en t parameters bij φ _f = 0.02, E _f = 100 GPa en E _ik = 50 GPa. Volgens figuur 5a geven de kleinste nanodeeltjes en de dikste interfase het hoogste niveau van φ _ik als 0,8 wat het nanocomposiet aanzienlijk versterkt. Dit niveau van φ _ik is meer dan φ _f demonstreren van de effectieve rol van R en t parameters in de prestaties van nanocomposieten. Verder, φ _ik neemt af tot ongeveer 0 bij R> 30 nm, d.w.z. een dikke interfase (t = 25 nm) kan geen hoge φ . maken _ik in polymeer nanocomposieten wanneer grote nanodeeltjes worden opgenomen in de polymeermatrix. Dit voorval toont de belangrijke rol van de grootte van nanodeeltjes bij de vorming van interfasegebieden. Dus de grootte van nanodeeltjes verandert de interfase-eigenschappen aanzienlijk, wat onthult dat de aggregatie/agglomeratie van nanodeeltjes meestal de interfaseconcentratie verlaagt, wat een slechte modulus en sterkte in nanocomposieten veroorzaakt [5, 45]. Er moet worden vermeld dat de interfasegebieden elkaar kunnen overlappen in de systemen met een hoge vulstofconcentratie. Daarom is de uitgedrukte vergelijking voor φ _ik (Vgl. 10) is redelijk voor normale nanocomposieten met een laag vulstofgehalte.

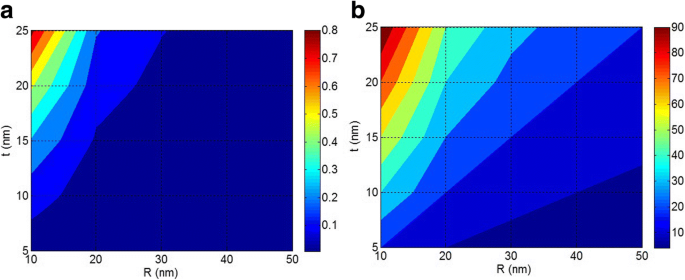
De correlatie van a ϕ _ik en b een interfase parameter naar R en t parameters bij ϕ _f = 0.02, E _f = 100 GPa en E _ik = 50 GPa

Afbeelding 5b toont ook de effecten van R en t niveaus op a interfase parameter. een neemt toe met kleine nanodeeltjes en dikke interfase, terwijl het minder waarden geeft (minder dan 10) bij R> 40 nm en t < 10 nm. Dit bewijs laat zien dat een hangt af van beide R en t parameters. Sinds een hoge a parameter verbetert de Young's modulus van nanocomposieten [38], kleine nanodeeltjes en dikke interfase zijn wenselijk voor nanocomposietenprestaties. Volgens figuur 5b zijn de aggregaten/agglomeraten van nanodeeltjes (hoge R ) produceren een lichte a gebeurtenis door dikke interfase. Dit voorval geeft aan dat een sterke interfase geen geweldige a . kan geven of hoge modulus wanneer de nanodeeltjes worden geaggregeerd/geagglomereerd in nanocomposieten. Hierdoor veroorzaken de aggregaten/agglomeraten van nanodeeltjes negatieve effecten op de eigenschappen van polymere nanocomposieten. Op basis van de genoemde opmerkingen verzwakt de aggregatie/agglomeratie de voordelen van nanodeeltjes en eigenschappen van interface/interfase; daarom kunnen de nanodeeltjes geen sterke versterking bieden in polymeer nanocomposieten.

Conclusies

De effecten van vulstofgrootte en -dichtheid, evenals interfasedikte op de kenmerken van nanodeeltjes en de interface/interfase-eigenschappen werden bestudeerd door eenvoudige vergelijkingen. Ook werden de aggregaten/agglomeraten van nanodeeltjes aangenomen als grote deeltjes en werden hun invloeden op de interfaseparameters en de treksterkte van nanocomposieten besproken. De kleine omvang en lage dichtheid veroorzaken significante niveaus voor het aantal, het oppervlak, de verstijvingsefficiëntie en het specifieke oppervlak van nanodeeltjes. Slechts 2 g kleine en goed verspreide nanodeeltjes (R = 10 nm) met d _f = 2 g/cm³ kan ongeveer 250 m² . produceren grensvlak met polymeermatrix. Aan de andere kant verzwakken grote afmetingen en aggregaten/agglomeraten de positieve eigenschappen van nanodeeltjes in nanocomposieten. Kleine nanodeeltjes en dikke interfase presenteren de hoge niveaus voor B parameter, treksterkte, interfase volumefractie en a interfase parameter. B neemt af tot minder dan 3 wanneer de grootte van nanodeeltjes groeit tot ongeveer 40 nm en de interfasedikte afneemt tot minder dan 10 nm. Echter, B = 13 wordt verkregen door de kleinste nanodeeltjes (R = 10 nm) en de dikste interfase (t = 25 nm). Dit voorval bevestigt dat de eigenschappen van het grensvlak/interfase afhankelijk zijn van de grootte van de nanodeeltjes naast de interactie/adhesie van het grensvlak. Bovendien produceren grote nanodeeltjes lage grensvlak-/interfase-eigenschappen en een slechte treksterkte, zelfs bij een hoge interfasedikte, wat de hoofdrol van de deeltjesgrootte onthult. De kleinste nanodeeltjes en de dikste interfase geven het hoogste niveau van φ _ik , terwijl φ _ik neemt af tot ongeveer 0 bij R> 30 nm. Dit bewijs toont aan dat alleen een dikke interfase (t = 25 nm) kan geen hoge φ . maken _ik wanneer grote nanodeeltjes of aggregaten/agglomeraten aanwezig zijn in nanocomposieten. Dienovereenkomstig hebben de geaggregeerde/geagglomereerde nanodeeltjes een negatief effect op de grensvlak-/interfase-eigenschappen en treksterkte van polymere nanocomposieten.

De anionische oppervlakteactieve stof/ionische vloeistoffen geïntercaleerd gereduceerd grafeenoxide voor krachtige supercondensatoren Een onderzoek naar de variabiliteit in contactresistief willekeurig toegankelijk geheugen door stochastisch vacaturemodel

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal