Percolatiemagnetisme in ferro-elektrische nanodeeltjes

Achtergrond

Fabricage en intensieve studies van nanodeeltjes van diëlektrische oxiden, die niet-magnetisch zijn in een bulk, onthulden het ferromagnetisme daarin, bijvoorbeeld in HfO₂ [1], TiO₂ [2,3,4], ZnO [5,6,7], SnO₂ [7, 8], KTaO₃ [9], en KNbO₃ [10]. Verschillende oorzaken van de verschijnselen werden overwogen, zoals metalen clusters, secundaire fasen, gebonden magnetische polarons, ladingsdragers en zuurstofvacatures [2, 3, 5, 8,9,10,11,12,13]. De laatste worden gehybridiseerd in de buurt van het oppervlak van nanodeeltjes, waardoor ze magnetische eigenschappen krijgen [12, 13]. Momenteel zijn de verklaringen nog steeds controversieel en bestaat er geen consensus over de bron van ferromagnetisme. Daarom gaat de onderzoeksactiviteit verder in de richting.

Onder ferro-elektriciteit, recentelijk, in nanokristallen (gemiddelde deeltjesgrootte is 80 nm) van kaliumtantalaat en kaliumniobaat, geproduceerd door de nieuwe technologie van de metaal (Ta of Nb) oxygenatie in gesmolten kaliumnitraat [14], magnetische resonantie en statische magnetisatiemethoden experimenteel het uiterlijk van een ferromagnetisch subsysteem vastgesteld samen met een paramagnetisch subsysteem [10, 15, 16]. Dit effect is afwezig in grotere kristallen (met afmetingen> 200 nm) van de verbindingen die met dezelfde technologie zijn verkregen. De verbindingen zijn in de bulk niet-magnetisch. De opzettelijke doping van kaliumtantalaat (KNbO₃ ) en kaliumniobaat (KTaO₃ ) nanokristallen door ijzer en mangaan afzonderlijk resulteerden in de toename van de paramagnetische component, terwijl het ferromagnetische subsysteem onveranderd bleef [15, 16]. Er is gesuggereerd dat de reden voor het verschijnen van de magnetische eigenschappen van ongerepte ferro-elektrische nanokristallen magnetische defecten zijn, die zowel ijzeronzuiverheidsatomen kunnen zijn, die metalen clusters vormen op het oppervlak van de nanodeeltjes, als zuurstofvacatures [9]. Naast de bovengenoemde experimentele methoden was deze veronderstelling gebaseerd op de gegevens van elementanalyse en theoretische schattingen.

Om het microscopische mechanisme van het waargenomen fenomeen te bepalen, analyseren we in dit werk de situatie met behulp van een percolatietheorie. Percolatietheorie beschreef vrij goed een aantal effecten in ongeordende magnetische systemen, eerder in ferrodiëlektrica [17], later in verdunde magnetische halfgeleiders (bijv. [18,19,20,21]). Magnetisch subsysteem wordt behandeld als een gebonden magnetisch polaron in verdunde halfgeleiders. Dit model werd eerst voorgesteld door de auteurs van [22] en vervolgens ontwikkeld door de auteurs van Refs. [11, 23].

Uitgaande van de dominante rol van zuurstofvacatures, gebruiken we het model van gebonden magnetische polaronen en vinden we de percolatiestraal waarbij de uitwisselingsinteracties tussen elektronen gevangen in zuurstofvacatures gemedieerd door magnetische onzuiverheidionen een ferromagnetische oppervlakteordening induceren in ferro-elektrische KTaO₃ en KNbO₃ nanodeeltjes.

Experimentele gegevens en model van ferromagnetische bestelling

Om het voorgestelde model van ferromagnetische ordening te rechtvaardigen, beschrijven we eerst de experimentele gegevens die zijn verkregen over de ferro-elektrische nanodeeltjes КTaO₃ (KTO) en KNbO₃ (KNO).

De onderzochte ferro-elektrische nanodeeltjes zijn nominaal zuiver, d.w.z. er zijn geen doteermiddelen speciaal ingebouwd. Elementaire analyse uitgevoerd met een Shimadzu ICPE-9000 inductief gekoppeld plasma-atomaire emissiespectrometer (ICP-AES) toont echter aan dat Fe in beide materialen aanwezig is als onvermijdelijke onzuiverheid in de hoeveelheid van 0,06 mol.% in КTaO₃ en 0,008 mol.% in KNbO₃ . Het is ook bekend dat de zuurstofvacatures altijd bestaan ​​in oxide-ferro-elektriciteit, zoals het perovskiet-type (algemene formule ABO₃ ), wat resulteert in een zekere mate van niet-stoichiometrie in deze verbindingen. Experimenteel is aangetoond dat twee magnetische subsystemen (paramagnetisch en ferromagnetisch) aanwezig zijn in nanokristallen KTaO₃ en KNbO₃ [9, 10, 15]. Paramagnetisch subsysteem bestaat uit afzonderlijke niet-interagerende magnetische Fe ³⁺ ionen in KTaO₃ , en Fe ³⁺ en Mn ²⁺ ionen in KNbO₃ . Bovendien bevat de structuur van het paramagnetische centrum, zoals bepaald uit elektronenparamagnetische resonantie (EPR)-metingen, een zuurstofvacature V(O), die de centrumsymmetrie verlaagt [9, 15]. Ter illustratie:twee soorten paramagnetische centra, van axiale en rhombische symmetrie, waarbij Fe ³⁺ ion vervangt Ta ⁵⁺ (of Nb ⁵⁺ ) ion, worden getoond in Fig. 1. Om de ladingscompensatie te bereiken, worden één (axiaal centrum) of twee (ruitvormig centrum) zuurstofvacatures V(O) gevormd in de structuur van deze centra.

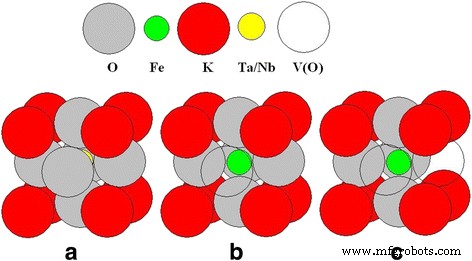
Modellen van laagsymmetrische paramagnetische centra van Fe ³⁺ in KTaO₃ en KNbO₃ nanokristallen. een Eenheidscel zonder defecten, b axiaal Fe ³⁺ -V(O) midden, en c ruitvormige Fe ³⁺ -2 V(O) centrum

Zoals gesuggereerd in de artikelen [9, 15], is een ferromagnetisch subsysteem een ​​(een) oppervlaktecluster(s) bestaande uit ijzeratomen en zuurstofvacatures. Thermisch gloeien in een zuurstofatmosfeer, uitgevoerd in het artikel [9], laat zien dat zuurstofvacatures zeker bijdragen aan de vorming van ferromagnetisme in deze verbindingen. Aan de ene kant hybridiseren de vacatures en worden magnetisch dicht bij het oppervlak van nanodeeltjes [13]. Aan de andere kant worden elektronen die inherent ontstaan ​​in niet-stoichiometrische oxiden vaak gevangen door zuurstofvacatures. In beide gevallen heeft de zuurstofvacature spin S = ½ en draagt ​​bijbehorend magnetisch moment.

De aanwezigheid van oppervlakte-ferromagnetisme is experimenteel bevestigd door atoomkrachtmicroscopie (AFM) in een magnetische veldgradiëntmodus. Fig. 2 toont bijvoorbeeld de oppervlaktebeelden die zijn verkregen voor het monster van nanokristallijn KTaO₃ . Magnetische krachtmicroscopie (MFM) metingen werden uitgevoerd door Dimension 3000 NanoScope IIIa scanning probe microscoop voor het in kaart brengen van de ruimtelijke variatie van de magnetisatiestructuur van de out-of-plane component van het magnetische strooiveld van de KTaO₃ monster oppervlak. Magnetische krachtgradiënten werden gemeten met behulp van een tweetrapstechniek (liftmodus) waarbij topografie werd gescand bij de eerste passage in de tikmodus en vervolgens werden de magnetische veldgradiënten in kaart gebracht bij de tweede met behulp van oscillatiefrequentieverschuiving van de sonde die over het oppervlak beweegt (lift hoogte was 300 nm). De met kobalt gecoate Veeco magnetische krachtsondes (MESP) met een coërciviteit van ~400 Oe, magnetisch moment van de 1 · 10 ⁻¹³ emu en 25 nm nominale punt apex radius werden gebruikt. Vóór de metingen werd de sonde gemagnetiseerd met behulp van een sterke permanente magneet waarbij het veld langs de verticale as van de punt was uitgelijnd.

Oppervlaktebeelden met gemagnetiseerde gebieden in de KTaO₃ nanokristallen. een Toewijzing van magnetische veldgradiënten en b oppervlaktereliëf afbeelding

Ook zijn de statische magnetisatielussen experimenteel verkregen bij twee temperaturen voor elke verbinding, bij 290 en 150 K voor KTaO₃ en op 290 en 110 K voor KNbO₃ . De experimentele magnetisatiecurven worden beschreven door de formule:

Hier, M _S is de verzadigingsmagnetisatie, H is een statisch magnetisch veld, en V ₀ is het volume van oneindige (in feite gesloten over een nanodeeltjesoppervlak) magnetische cluster. Verzadigingsmagnetisatie werd gedefinieerd volgens de formule (7) uit [20]:

waar S ₁ en S ₂ zijn V(O) en Fe ³⁺ magnetische momenten (spins van V(O) en Fe ³⁺ zijn respectievelijk 1/2 en 5/2), N ₁ en N ₂ zijn de getallen van respectievelijk V(O) en Fe. Gegeven waarden N ₂ komen overeen met de concentraties 0,06 mol.% voor KTO en 0,008 mol.% voor KNO verkregen uit elementanalyse, waarden N ₁ werden dienovereenkomstig bepaald. De aanpasresultaten worden getoond in Fig. 3. Voor een beschrijving van de hysteresislussen bij lage magnetische velden, gebruikten we de verschuiving van formule (2) op de waarde van het coërcitiefveld, H _c . Parameters voor elke curve worden gegeven in Tabel 1.

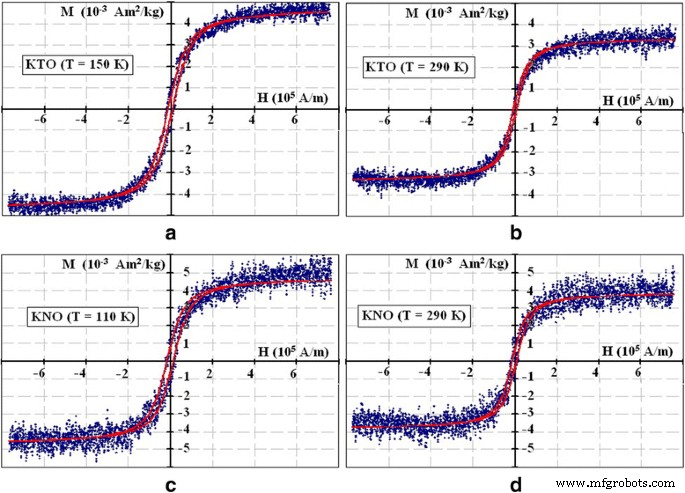
Statische magnetisatiecurven. Magnetisatiecurven in KTaO₃ (een , b ) en KNbO₃ (c , d ) nanodeeltjes bij T = 150, 290, 110 en 290 K. Aanpassingsparameters staan ​​vermeld in Tabel 1

Volgens het aantal magnetische spins geschat op basis van de EPR-gegevens [10, 15], is de procentuele verhouding tussen de paramagnetische en ferromagnetische subsystemen 14/86 in het kaliumtantalaat in nanogrootte, en het is 40/60 voor kaliumniobaat. Het grotere aantal paramagnetische centra in kaliumniobaat wordt veroorzaakt door de aanwezigheid van ongecontroleerde mangaanverontreiniging naast de ijzerverontreiniging. Merk op dat het aantal magnetische spins dat een ferromagnetisch subsysteem vormt, verkregen uit eerdere experimenten, niet voldoende is om de magnetische orde op lange afstand in het gehele volume van de nanodeeltjes vast te stellen. Daarom nemen we aan dat de belangrijkste bijdrage aan het ferromagnetisme magnetische spins zijn, die zich dichtbij het oppervlak van de deeltjes bevinden, namelijk in de ondergrondse laag verrijkt met defecten. Zoals vermeld in [24] is de oppervlaktelaag verrijkt met polaire defecten ongeveer 10 roosterconstante dik. Aan de andere kant, de auteurs van Ref. [25] suggereren dat de laag verrijkt met magnetische defecten in semi-oneindig kristal 1 roosterconstante dik is. Aangezien de complexen Fe ³⁺ -V(O) zowel polaire als magnetische defecten zijn, veronderstellen we dat de defectlaag nabij het oppervlak 5 roosterconstanten heeft in onze berekeningen. In KTaO₃ en KNbO₃ , komt de laag overeen met 2 nm. Om de percolatiecondities afgeleid in het artikel [17] te gebruiken, nemen we aan dat de verdeling van defecten uniform is in de nabije oppervlaktelaag. Volgens transmissie-elektronenmicroscopie (TEM) gegevens (Fig. 4, zie ook Fig. 1 in Ref. [9] en Fig. 2 in Ref. [26]), de vorm van КTaO₃ en KNbO₃ nanodeeltjes kunnen worden gemodelleerd door een kubus. De grootteverdeling van kristallieten in elke verbinding verkregen uit de TEM-gegevens wordt weergegeven in Fig. 5.

TEM-afbeelding van de KTaO₃ nanodeeltjes

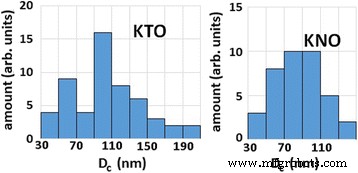
De grootteverdeling van kristallieten in KTaO₃ en KNbO₃

Op basis van experimenteel verkregen magnetisatiecurven, met name rekening houdend met de gegeven aantallen V(O) en Fe (zie tabel 1), zien we de dominante rol van de zuurstofvacatures bij magnetisatie. Bij deze aanname kan een uitwisselingsinteractie worden geïnitieerd door elektronen die zijn opgesloten in zuurstofvacatures en worden gemedieerd door magnetische onzuivere Fe-ionen. Een dergelijke interactie is overwogen in het model van gebonden magnetische polarons. Dit model werd voor het eerst voorgesteld door de auteurs van [22] om het optreden van ferromagnetisme in verdunde magnetische halfgeleiders te beschrijven. Schematisch wordt ons model weergegeven in Fig. 6.

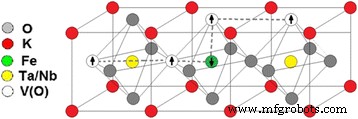
Model van magnetische ordening op lange afstand tussen elektronen gevangen in zuurstofvacatures in de niet-stoichiometrische KTaO₃ /KNbO₃ verbinding

Theoretische modellering binnen percolatiebenadering

Om de kritische concentratie van totale defecten te bepalen, die kunnen leiden tot de vorming van magnetische polarons, gebruiken we een percolatiebenadering. Met behulp van de criteria van de percolatietheorie werd in het werk [17] getoond hoe de percolatiedrempel van de magnetische orde op lange afstand wiskundig wordt vastgesteld. Het weglaten van de details van de benaderingen en principes uit Ref. [17], we zullen ons concentreren op de kenmerken die in onze berekeningen worden gebruikt en het algemene verloop van de berekening beschrijven.

In overeenstemming met de TEM-gegevens (zie Fig. 4), beschouwd als KTaO₃ en KNbO₃ nanodeeltjes kunnen worden gemodelleerd door een kubus. Het kubische rooster met een roosterconstante van 0,4 nm werd gebruikt. In de nabije oppervlaktelaag van 2 nm dikte (dat is 5 eenheidscellen) (achtergrond is hierboven gegeven, zie ook Refs. [24] en [25]) met willekeurig verdeelde defecten, Fe-atomen en zuurstofvacatures V(O), rekening houdend met het feit dat de verdeling van ijzeratomen uniform is. Volgens de modellen van axiale en rhombische centra (zie Fig. 1), de aanwezigheid van Fe-atoom in het centrum van de eenheidscel (wanneer het Nb- of Ta-atomen in de KTaO₃ vervangt of KNbO₃ rooster) gaat gepaard met het verschijnen van V(O) op de rand(en) van de cel. Met enige waarschijnlijkheid kan één zuurstoftekort V(O) of twee lege plekken 2 V(O) optreden. De kans is in ons geval 50% wat overeenkomt met de experimenteel bepaalde verhouding van de axiale (Fe-V(O)) en rhombische (Fe-2 V(O)) centra in KTaO₃ en KNbO₃ [9, 10, 15]. De defecten werden gemodelleerd door bollen in onze berekeningen, waarbij de stralen van ijzerionen en zuurstofleegte r zijn (Fe ³⁺ ) = 0.064 nm en r (V(O)) = 0,132 nm, respectievelijk. De afstand d tussen de defecten werd gedefinieerd als de afstand tussen het oppervlak van de bollen en niet tussen hun middelpunten. Als we de coördinaten van willekeurige defecten kennen, namelijk Fe-atomen en V(O)-vacatures, berekenen we de afstand d tussen hen. Het resultaat van de verdeling van defecten wordt schematisch weergegeven in Fig. 7.

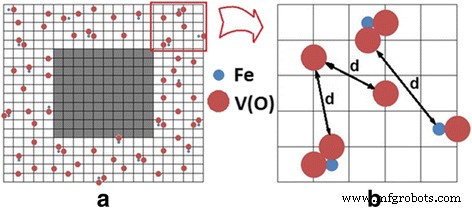
Verdeling van defecten in de oppervlaktelaag. een Licht gebied geeft de onderliggende defectlaag weer. Grijs gebied weerspiegelt de diepte van nanodeeltjes, waar defecten bijna afwezig zijn in vergelijking met de ondergrondse laag. De evenredigheid tussen de grootte van het ondergrondse defectgebied en de defectvrije binnenkern is in deze figuur gebroken voor een duidelijkere weergave van de defectenverdeling in de ondergrondse laag. Fe-atomen zijn gelijkmatig verdeeld in de diepte van de defecte laag, de zuurstofvacatures V(O) bevinden zich in de buurt van Fe-atomen. b Zoom van de defecte laag (a ); d is de afstand tussen defecten

Volgens de percolatietheorie treedt de magnetische orde op lange afstand in het systeem op zodra de oneindige cluster zich vormt (zie bijv. p.235 in Ref. [17]). De afstand tussen de defecten, die een oneindig cluster vormen en daarom voldoen aan de percolatievoorwaarde ("percolatiedrempel"), wordt gedefinieerd als een percolatiestraal, R _perc . Om de percolatiestraal te bepalen, is de berekening uitgevoerd voor de nanodeeltjes van verschillende groottes, om ervoor te zorgen dat daadwerkelijk aan de percolatievoorwaarde wordt voldaan. Voor dit geval blijft de verhouding tussen het aantal magnetische defecten in de oneindige cluster en het totale aantal magnetische defecten in het systeem onveranderd in deeltjes van verschillende groottes. De grootte van de nanodeeltjes is D × D × D eenheidscellen, waarbij D = 20, 30, 40. Om de afhankelijkheid van de percolatiestraal van de concentratie van magnetische defecten te bepalen, werden de berekeningen uitgevoerd voor de concentraties in tabel 2. Hier, n ₁ definieert de concentratie van zuurstofvacatures die zich niet in de buurt van Fe-atomen bevinden, n ₂ is de concentratie van Fe-atomen, en n is een totale concentratie van defecten. Merk op dat we berekeningen uitvoeren voor twee gevallen. Voor geval I, n ₁ /n ₂ = const en n varieert. Voor geval II, n ₂ = const en n ₁ varieert.

Om de percolatiestraal R . te bepalen _perc , gebruiken we de volgende procedure. Voor elke concentratie stellen we een bepaalde waarde in R dat werd gevarieerd van 0,1 tot 5,9 nm met een toename van 0,2 nm. De afstand d tussen de defecten werd vergeleken met de waarde R (voor elke R waarde). Alle magnetische defecten zijn dus verdeeld in twee groepen. Als de afstand d _ij tussen de dichtstbijzijnde i th en j het defect is kleiner dan of gelijk aan de R , d.w.z. d _ij ≤ R , classificeren we deze defecten in een groep, waarin er een magnetische koppeling is tussen de defecten; anders, als d _ij > R , verwijzen we dergelijke defecten naar de andere groep, waar de koppeling tussen defecten afwezig is (d.w.z. verbroken). Als resultaat van de berekening krijgen we de matrix van m × m , welke elementen Booleaanse waarden 1/0 zijn (aan-/afwezigheid van koppeling tussen de i th en j de gebreken). Hier, m is het aantal defecten in de ondergrond in het deeltje van een bepaalde grootte. Vervolgens vinden we, gebruikmakend van het principe van Markov-ketens, de magnetische clusters (d.w.z. aggregaten van punten {Fe, V (O)}), die indirect interageren. Voor dit doel hebben we de eerder genoemde m × m matrix tot de macht m en krijg een nieuwe matrix m × m , welke elementen Booleaanse waarden 1/0 zijn (aan-/afwezigheid van gemedieerde interactie tussen de i th en j de gebreken). De maximale som van de matrixlijn komt overeen met de grootte van de grootste cluster voor een gegeven deeltjesgrootte. Soortgelijke berekeningen werden uitgevoerd voor elke waarde van R en de grootte van de nanodeeltjes. Verkregen resultaten voor een van de concentraties n = 0.6117 nm ⁻³ worden weergegeven in Tabel 3. Het cursieve gedeelte in de tabel komt overeen met de R = R _perc waarde die de percolatiestraal is R _perc = 1.7 nm. Percolatiestraal R _perc werd gevonden in overeenstemming met de hierboven beschreven percolatiedrempel.

Figuur 8 toont schematisch de vorming van de oneindige cluster in de deeltjes van verschillende groottes.

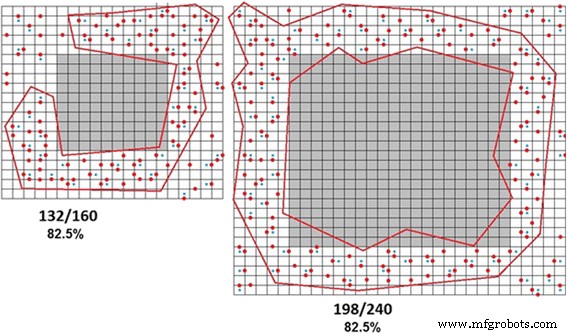
Oneindige clustervorming in de deeltjes van verschillende grootte. De percolatiedrempel is 82,5%, gedefinieerd als de procentuele verhouding van defecten in het cluster is niet afhankelijk van de deeltjesgrootte, zoals verwacht

Resultaten en discussie

Afbeelding 9a toont de afhankelijkheid van de percolatiestraal R _perc over de concentratie van defecten voor het geval I, d.w.z. wanneer n ₁ /n ₂ = const en n varieert. De ononderbroken curven worden uitgezet met behulp van de formule

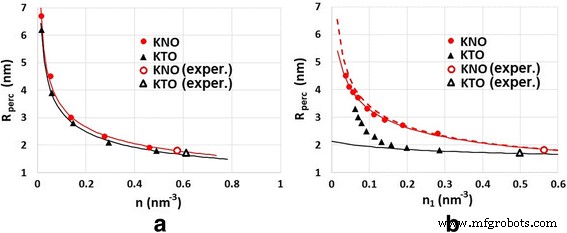
Percolatiestraal versus de concentratie van defecten voor twee gevallen:a n ₁ /n ₂ = const, n varieert en b n ₂ = const, n ₁ varieert. Punten worden numeriek berekend in het kader van ons model, vaste curven zijn gebaseerd op de formule (1). Punten gemarkeerd met labels komen overeen met de bestudeerde materialen (KTaO₃ en KNbO₃ )

$$ {R}_{\mathrm{perc}}=\frac{a}{\sqrt[3]{n}}- b $$ (3)

met parameters a = 1.6 en 1.7 voor respectievelijk KTO en KNO, en b = 0,25 nm voor zowel KTO als KNO. De eerste term in de formule (3) is consistent met de vergelijking (4) in Ref. [20] voor een percolatiestraal, \( {R}_{\mathrm{perc}}=\frac{a}{\sqrt[3]{n}}. \)

De waarde van R _perc is een bepaalde kritische waarde, voor R> R _perc , zal het oneindige cluster worden gevormd, wat binnen de noodzakelijke voorwaarde is van het verschijnen van de magnetische orde op lange afstand in het kader van de percolatietheorie. We namen aan dat de straal R _perc is hetzelfde voor de paren Fe-Fe, V(O)-V(O) en V(O)-Fe. Op basis van de berekende resultaten en experimentele feiten kunnen we echter stellen dat de straal R _perc mag niet kleiner zijn dan 1,6 nm voor KTaO₃ en 1,7 nm voor KNbO₃ .

Laten we de formule (3) in meer detail bekijken. Fysieke betekenis van de uitdrukking \( 1/\sqrt[3]{n} \) is de afstand tussen defecten die deelnemen aan de magnetische uitwisseling voor het verschijnen van ordening op lange afstand. De waarde a kan zowel kleiner als groter zijn dan 1. Wanneer de straal R _perc komt overeen met de gemiddelde afstand tussen defecten, de waarde a = 1, en dus \( {R}_{\mathrm{perc}}=1/\sqrt[3]{n} \). Wanneer het aantal willekeurige magnetische koppelingen, dat wordt gevormd door de interactie tussen defecten op een afstand kleiner dan het gemiddelde, voldoende is voor de vorming van een oneindige cluster, waarde a is kleiner dan 1. Bijvoorbeeld a = 0,86 in het werk [17]. Het blijkt dat de R _perc is 1,6-1,7 keer hoger dan de gemiddelde afstand tussen defecten in ons geval. Dit kan als volgt worden uitgelegd.

De waarde van de gemiddelde afstand tussen defecten is zinvol voor een uniforme verdeling van defecten in de ondergrond. De verdeling van Fe-atomen wordt als quasi-uniform beschouwd, maar rekening houdend met het feit dat de Fe-atomen in het midden van de cel zijn geplaatst, zijn hun posities discrete ruimtelijke coördinaten, wat ook van invloed is op de waarde a in de vergelijking 3, en de locatie van zuurstofvacatures V(O) is niet uniform omdat ze zich altijd in de buurt van Fe-atomen bevinden (zie figuur 6). De afstand tussen Fe-atomen is dus veel groter dan de afstand tussen het Fe-atoom en de zuurstofvacature V(O). Daarom is de straal R _perc hangt eigenlijk niet af van de gemiddelde afstand tussen alle defecten, maar hangt af van de gemiddelde afstand tussen defecten in verschillende eenheidscellen (dit kan de afstand zijn tussen de Fe-Fe, V(O)-V(O), V(O) )-Fe). De aanwezigheid van zuurstofvacatures in de buurt van de Fe-atomen verkleint de afstand tussen de defecte cellen enigszins vanwege de kleinheid van de V(O)-Fe-afstand in vergelijking met de Fe-Fe-afstand. Dat betekent dat we in dit geval eigenlijk te maken hebben met de gemiddelde afstand tussen Fe-atomen.

Aftrekken van de tweede component b = 0,25 nm in vergelijking (3) kan als volgt worden uitgelegd. Doorgaans wordt de afstand tussen defecten in deze vergelijking gedefinieerd als de afstand tussen de middelpunten van defecten, als een defect wordt gesimuleerd als een punt. In onze berekeningen, R _perc wordt gedefinieerd als de afstand tussen de oppervlakken van de bol waarin we het (de) defect(en) hebben geplaatst. Dus de waarde R_perc , geschat als de afstand tussen de oppervlakken van de bollen, verschilt van de R _perc geschat als de afstand tussen de centra ten minste op de som van twee stralen van op elkaar inwerkende defecten. De som kan variëren van 0,128 nm voor Fe-Fe-interactie (figuur 10a) tot 0,264 nm voor V(O)-V(O)-interactie (figuur 10c). Bovendien, aangezien de afstand tussen het Fe-atoom en de dichtstbijzijnde vacature V(O) veel kleiner is dan de berekende, die nodig is om een ​​koppeling tussen defecten tot stand te brengen, zal in bepaalde gevallen R _perc kan worden gedefinieerd als de afstand V(O)-Fe of V(O)-V(O) van verschillende cellen (zie figuur 10b, c). Wanneer het aantal V(O) toeneemt, neemt ook het aantal gevallen in Fig. 10b, c respectievelijk toe. Dienovereenkomstig is de berekende waarde van b = 0,25 nm geeft aan dat er voornamelijk een uitwisselingsinteractie plaatsvindt tussen de elektronen die zijn opgesloten in zuurstofvacatures.

Vermindering van R _perc voor interactie tussen verschillende defecten (a -c ) in vergelijking met een uniforme verdeling van Fe (blauw ) atomen wordt veroorzaakt door de aanwezigheid van zuurstofvacatures V(O) (rood )

Afbeelding 9b toont de afhankelijkheid van de percolatiestraal R _perc over de concentratie van defecten voor geval II, d.w.z. wanneer n ₂ = const en n ₁ varieert. Hier wordt de invloed van Fe-atomen groter als n ₁ neemt af. Dit is meer uitgesproken voor KTO (zwarte ononderbroken curve in Fig. 9b). Desalniettemin hebben we geprobeerd de berekende gegevens te passen met behulp van de formule (3) met parameters a = 0.66 en b = 0,15 nm. De waarde van b geeft aan dat de relatieve hoeveelheid directe V(O)-V(O)-interacties afneemt, terwijl de hoeveelheid indirecte interacties via Fe-atomen toeneemt.

Conclusies

We beschouwen microscopisch mechanisme dat leidt tot het ontstaan ​​van ferromagnetische ordening in ferro-elektrische KTaO₃ en KNbO₃ nanodeeltjes. Onze aanpak is gebaseerd op de magnetische percolatietheorie. Het beschrijft de vorming van magnetische oppervlaktepolarons waarin een uitwisselingsinteractie tussen ladingsdragers, d.w.z. elektronen, gevangen in zuurstofvacatures, direct of indirect plaatsvindt via magnetische Fe-atomen.

De afhankelijkheid van straal R _perc op de totale concentratie n van defecten bij constante n ₁ /n ₂ verhouding (n ₁ is de concentratie van zuurstofvacatures en n ₂ is de concentratie van Fe-atomen) wordt bepaald in het kader van de percolatietheorie. Bleek dat de afhankelijkheid goed wordt beschreven door de formule \( {R}_{\mathrm{perc}}=\frac{a}{\sqrt[3]{n}}- b \), waarbij de waarden van de parameters a = 1.6 en 1.7 voor respectievelijk KTO en KNO, en b = 0,25 nm voor zowel KTO als KNO. Het is gebleken dat de werkelijke magnetische percolatiestraal niet kleiner kan zijn dan 1,6 nm voor KTaO₃ en 1,7 nm voor KNbO₃ .

Met behulp van de berekende kritische concentratie van magnetische defecten worden experimenteel gemeten magnetische hysteresislussen goed beschreven door twee verschoven Langeven-type formules. Magnetisatieverzadigingswaarde M _S hangt af van de magnetische momenten van zuurstofvacatures V(O) en Fe ³⁺ ionen en hun hoeveelheden N ₁ en N ₂ , respectievelijk in de oneindige cluster als M _S = |S ₁ N ₁ − S ₂ N ₂ |, dat is in een volledige overeenkomst met Ref. [20].

Theoretische berekeningen beschrijven adequaat de experimentele resultaten die zijn verkregen in ferro-elektrische KTaO₃ en KNbO₃ nanodeeltjes gesynthetiseerd door oxidatie van metallisch tantaal in gesmolten kaliumnitraat met toevoeging van kaliumhydroxide, die een zwak ferromagnetisme vertonen, terwijl deze verbindingen in bulk niet-magnetisch zijn.

Afkortingen

AFM:

Atoomkrachtmicroscopie

MESP:

Met kobalt gecoate magnetische krachtsondes

MFM:

Magnetische krachtmicroscopie

TEM:

Transmissie-elektronenmicroscopie