home Productietechnologie Fabricage-apparatuur
Industriële fabricage
Industrieel internet der dingen | Industriële materialen | Onderhoud en reparatie van apparatuur | Industriële programmering |
home  MfgRobots >> Industriële fabricage >  >> Industrial materials >> Nanomaterialen

Elektrisch gestuurde vallei pseudomagnetische weerstand in grafeen met Y-vormige Kekulé-roostervervorming

Abstract

We stellen een nieuwe methode voor voor het reguleren van de pseudomagnetoweerstand van de vallei in op ballistische grafeen gebaseerde vallei-veldeffecttransistoren door rekening te houden met de Y-vormige Kekulé-roostervervorming en elektrische barrière. Het apparaat omvat dalinjectie en daldetectie door bron en afvoer van ferromagnetische spanning. De manipulatie van de vallei in het kanaal wordt bereikt via de Y-vormige Kekulé-roostervervorming en elektrische barrière. Het centrale mechanisme van deze apparaten ligt op Y-vormige Kekulé-roostervervorming in grafeen die een dalprecessie kan veroorzaken, waardoor de daloriëntatie van kanaalelektronen en dus de stroom die bij de afvoer wordt verzameld, wordt gecontroleerd. We ontdekten dat de externe afstemspanning ervoor zorgt dat de pseudo-magneetweerstand van het dal oscilleert tussen positieve en negatieve waarden en dat een kolossale pseudo-magneetweerstand van het tunneldal van meer dan 30.000% kan worden bereikt. Onze resultaten suggereren dat de synergie van valleytronics en digitale logica nieuwe paradigma's kan bieden voor op valleytronic gebaseerde informatieverwerking en omkeerbaar computergebruik.

Inleiding

Grafeen, dat een tweedimensionale laag koolstofatomen is, die een uitstekende draaggolfmobiliteit heeft en het dunst mogelijke kanaal biedt voor gebruik bij het ontwerpen van metaaloxide-halfgeleider-veldeffecttransistoren [1]. Semenov heeft een spin-veldeffecttransistor voorgesteld door een grafeenlaag als kanaal [2] te gebruiken, wat spin-injectie en spindetectie door ferromagnetische bron en afvoer omvat, en de spinmanipulatie in het kanaal wordt bereikt via elektrische besturing van de elektronenuitwisseling interactie met een ferromagnetische poort. Bovendien is de spin-baaninteractie van Rashba een ander veelbelovend hulpmiddel voor de spincontrole in grafeen [3]. De spin-baan interactie van Rashba kan een spin-precessie induceren, waardoor de spin-oriëntatie van kanaalelektronen wordt gecontroleerd. De spin-veldeffecttransistors inspireerden ook veel belangrijke onderzoeksideeën, zoals gigantische magnetoweerstand en tunnelmagnetoweerstand [3, 4]. De gigantische magnetoweerstand en tunnelmagnetoweerstand kunnen worden toegepast in digitale opslag- en magnetische sensortechnologieën.

Aan de andere kant hebben Dirac-elektronen in grafeen een extra dalvrijheidsgraad naast de conventionele ladings- en spin-tegenhangers. Vanwege het grote momentumverschil tussen de twee valleien en de onderdrukking van de intervalverstrooiing in schone grafeenmonsters [5-7], wordt aangenomen dat de vrijheidsgraad van de vallei hetzelfde effect uitoefent als de elektronenspin bij het dragen en manipuleren van informatie, wat leidt tot een nieuwe discipline die opkomt als valleytronics. Analoog aan de spin-veldeffecttransistor, wordt de vallei-veldeffecttransistor ook theoretisch voorgesteld in grafeen [8], dat bestaat uit een kwantumkanaal met één dimensie van grafeen met gaten dat is ingeklemd tussen twee grafeen-nanoribbons van fauteuils (bron en afvoer); vervolgens wordt het elektrische veld van de zijpoort op het kanaal aangelegd en moduleert het de dalpolarisatie van dragers als gevolg van de dal-baaninteractie, waardoor de hoeveelheid stroom die bij de afvoer wordt verzameld, wordt geregeld. Vanwege het feit dat de vallei-koppeling in grafeen lange tijd geen fysieke realiteit is geworden, zijn er echter weinig verdere onderzoeken op basis van de vallei-veldeffecttransistoren van grafeen en aanverwante studies. Recente experimenten van Gutierrez et al. [9] hebben een ongebruikelijke Y-vormige Kekulé (Kek-Y) bindingstextuur onthuld in het honingraatrooster op een grafeen-koper superrooster, waar een van de zes koolstofatomen in elke superroostereenheidscel geen koperatomen eronder heeft en een kortere naaste buur band. Verder heeft Gamayun aangetoond dat de textuur van de Kek-Y-binding een manier biedt voor een momentum-gecontroleerde vallei-precessie [10]. Beenakker et al. [11] toonde aan dat het Kek-systeem een ​​vallei-flip-effect kan veroorzaken via de Andreev-achtige reflectie. Recent Wang et al. [12] ontdekte dat de CC-bindingslengtemodulatie van het Kekulé-rooster dat de inversiesymmetrie van het systeem behoudt, kan worden gebruikt om de vrijheidsgraad van het dal te manipuleren op een vergelijkbare manier als het uitwisselingsveld voorafgaand aan de spin. Dit maakt het mogelijk om een ​​nieuw type vallei-veldeffecttransistor in grafeen te ontwerpen. Bovendien is er geen rapport over de gecombineerde effecten van de Kek-Y-roostervervorming op de pseudomagnetoweerstand van de vallei in grafeen. Valley pseudomagnetoweerstand [13, 14] is analoog aan de magnetoweerstand in magnetische tunnelovergang [15] waar de grootte van de spinstroom afhangt van de magnetische oriëntatie van de elektroden [4].

Methoden

In dit werk stellen we een nieuw type vallei-veldeffecttransistors (VFET's) voor voor op grafeen gebaseerde elektronen. Het ontwerp van het apparaat gaat uit van een ferromagnetische spanning (FM-S) source / drain voor gepolariseerde injectie / detectie in de vallei, die lijkt op conventionele spintransistor (zie figuur 1a). Valleirotatie in het grafeenkanaal is afhankelijk van Kek-Y-grafeensuperrooster [10-12], wat kan worden bereikt door een superrooster van grafeen dat epitaxiaal op Cu(111) groeit, waarbij de koperatomen in register zijn met de koolstofatomen [9]. Onder sommige koolstofatomen ontbreken echter koperatomen, wat resulteert in enkele periodieke koperatoomvacatures onder grafeen. Een dergelijke leegstand van substraatatomen leidt tot het aangaan van drie aangrenzende bindingen. Hier gebruiken we δ t om de energiewijziging van het springen van het elektron weer te geven dat overeenkomt met deze drie bindingen. We nemen aan dat het ferromagnetische grafeen is gemaakt van dezelfde FM-metalen streep. De twee magnetisaties van de source en drain zijn gericht langs de stroomrichting (de x as), die in de parallelle (P) of antiparallelle (AP) uitlijning kan zijn, met behulp van een extern in-plane magnetisch veld. In de Landau-meter heeft de magnetische vectorpotentiaal die voortkomt uit het randveld de vorm [16, 17] \(A(r)=A_{y}(x)\overrightarrow {y}\) met A j (x )=A j [Θ (−x )±Θ (x −L )], waarbij het plus(min)-teken overeenkomt met de P(AP)-configuratie van magnetisaties, Θ (x ) is de Heaviside-stapfunctie. Aan de andere kant nemen we aan dat dezelfde spanning wordt uitgeoefend op source en drain van de VFET's, wat kan worden veroorzaakt door een spanning op het substraat van het grafeen [18]. De elastische vervorming kan worden behandeld als een verstoring van de sprongamplitudes en fungeert als een ijkpotentiaal A S (r ). De spanning wordt ingesteld langs de x richting, in dit geval A S (r ) uniform langs de y as [16]. Voor de zekerheid nemen we een typisch glad profiel van zijn y component als A Sy (x )=A S [Θ (−x )+Θ (x −L )], waarbij A S is de amplitude. Bovendien wordt er ook een elektrische barrière toegepast in het Kek-Y-roostergebied, die kan worden afgestemd door externe voorspanning.

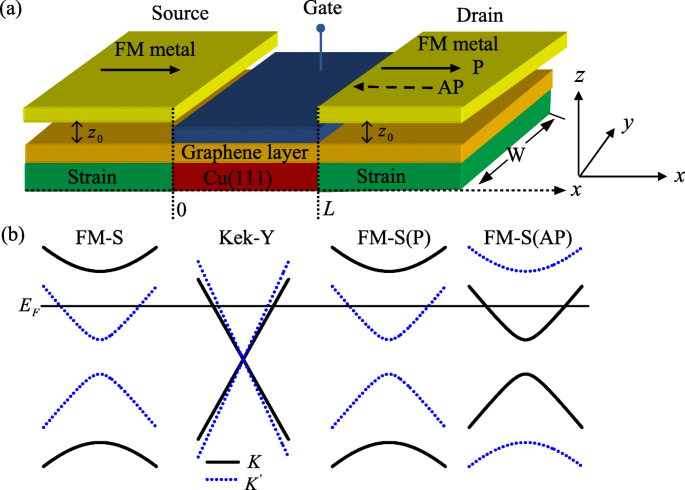
een Schematische illustratie van de VFET met behulp van een grafeenkanaal met Kek-Y-roostervervorming en een poortbias, die de daloriëntatie van kanaalelektronen regelt. De bron en afvoer zijn FM-S-grafeen, dat elektronen in een specifieke polarisatie injecteert en detecteert. Waar z 0 is de afstand tussen de grafeenlaag en de FM-streep. L is de kanaallengte, W is de breedte van het grafeenmonster in de y richting, en W ≫L . b Bandstructuur in de buurt van Dirac-punten. De horizontale lijn geeft de Fermi-energie aan (kleur online)

De voortplanting van quasideeltjes met lage energie-excitatie in de VFET's met Kek-Y grafeen superroosters kan worden beschreven door de volgende Hamiltoniaan met één deeltje [10-12]

$$ \begin{array} [c]{ll} H=&v_{F}(\mathbf{P}\cdot\sigma)+v_{\tau}(\mathbf{P}\cdot\tau)\Theta \left(x\right) \Theta\left(Lx\right) +\\ &U\sigma_{0}\tau_{0}\Theta\left(x\right) \Theta\left(Lx\right) + A_{M}(x)\sigma_{y}+\tau_{z}A_{S}(x)\sigma_{y}. \end{array} $$ (1)

Hier, σ en τ zijn de Pauli-matrices voor respectievelijk het subrooster en de vallei. P =(p x ,p j ) is het momentum van massaloze Dirac-elektronen, τ z =±1 voor K en \(K^{^{\prime }}\) valleien, v F =10 6 m/s is de snelheid van Dirac-elektronen in het ongerepte grafeen, en v τ ≃v F δ t /3t is de snelheidsmodificatieterm van het bindingscontractie-effect in het Kek-Y-rooster [12], waarbij t is de springenergie tussen de dichtstbijzijnde naburige citaten voor ongerept grafeen. U is de gate-afstembare potentiële barrière. A M (x )=e v F A j (x ) [19]. De eigenwaarden van de Hamiltoniaan in het grafeen met Kek-Y roostervervorming en elektrische barrière worden gegeven door

$$ E_{\alpha,\beta}=U+\alpha(\hbar v_{F}+\beta\hbar v_{\tau})\sqrt{k_{x\beta} ^{2}+k_{y} ^{2}}. $$ (2)

Hier, α =+1(−1) specificeert de geleidingsband (valentieband). β =± 1 geeft de twee dal-gesplitste subbanden van de geleidings- en valentiebanden aan. Vanwege de translationele invariantie in de y richting, de transversale golfvector k j wordt geconserveerd. De eigentoestanden in het grafeen met de homogene Kek-Y roostervervorming worden gekenmerkt door \(\Psi _{\beta }^{\pm }(k_{x\beta },k_{y})=\frac {1}{ N_{\beta }}\left (1,P_{\beta }^{\pm },Q_{\beta } ^{\pm },R_{\beta }^{\pm }\right)^{T} \), waarbij N β is de normalisatieconstante \(N_{\beta }=\left (1+P_{\beta }^{2}+Q_{\beta }^{2}+R_{\beta }^{2}\right)^ {\frac {1}{2}}\) en \(P_{\beta }^{\pm }, Q_{\beta }^{\pm }\), en \(R_{\beta }^{\ pm }\) zijn functies die als volgt zijn gedefinieerd:

$$ \begin{array} [c]{cc} P_{\beta}^{\pm}=&\frac{(EU)^{2}+\left(\hbar^{2}v_{F}^ {2}-\hbar^{2}v_{\tau} ^{2}\right)\left(k_{x\beta}^{2}+k_{y}^{2}\right)}{2 (EU)\hbar v_{F}(\pm k_{x\beta}-{ik}_{y})},\\ Q_{\beta}^{\pm}=&\frac{(EU)^ {2}-\left(\hbar^{2}v_{F}^{2}-\hbar^{2}v_{\tau} ^{2}\right)\left(k_{x\beta}^ {2}+k_{y}^{2}\right)}{2(EU)\hbar v_{\tau}(\pm k_{x\beta}-{ik}_{y})},\\ R_{\beta}^{\pm}=&\frac{(EU)^{2}-\left(\hbar^{2}v_{F}^{2}+\hbar^{2}v_{\ tau} ^{2}\right)\left(k_{x\beta}^{2}+k_{y}^{2}\right)}{2\hbar^{2}v_{F}v_{\ tau}(\pm k_{x\beta} -{ik}_{y})^{2}}. \end{array} $$ (3)

De transmissiekans van \(K^{^{\priem }}\) dal naar \(K(K^{^{\priem }})\) dal \(T_{K^{^{\prime }}, K(K^{^{\prime }})}\) kan worden berekend met behulp van de transfermatrixtechniek [20]. Volgens de Laudauer-Btittiker-formule wordt de vallei-afhankelijke conductantie gegeven door [21]:

$$ G_{K^{^{\prime}},K(K^{^{\prime}})}=G_{0} {\int_{-\frac{\pi}{2}}^{\ frac{\pi}{2}}} T_{K^{^{\prime}},K(K^{^{\prime}})}\cos(\phi_{0})d\phi_{0} . $$ (4)

Hier \(G_{0}=2e^{2}W/\left (v_{F}\pi ^{2}\hbar ^{2}\right)\left \vert E\right \vert \), W is de breedte van het grafeenmonster in de y richting, en ϕ 0 is de invalshoek ten opzichte van de x richting.

Voordat we verder gaan met de berekeningen, bespreken we de bandstructuur met k j =0, zoals weergegeven in figuur 1b. In het FM-S-brongebied wordt de energieband van grafeen geschreven als \(E=\alpha \sqrt {(\hbar v_{F}k_{x})^{2} +(A_{M}+\tau _{z}A_{S})^{2}}\). Men kan zien dat de vallei degenereert is lift en dat er verschillende gaten ontstaan ​​bij de K en \(K^{^{\prime }}\) punten omdat de totale vectorpotentiaal A M +A S handelend op K elektronen is hoger dan de totale vectorpotentiaal |A M −A S | inwerkend voor \(K^{^{\prime }}\) elektronen [19]. Dit geeft aan dat alleen \(K^{^{\prime }}\) elektronen door het FM-S-brongebied kunnen gaan wanneer de invallende energie zich in |A bevindt M −A S |<E <A M +A S [22, 23]. Evenzo kan in het FM-S-afvoergebied de energieband van grafeen worden geschreven als \(E=\alpha \sqrt {(\hbar v_{F}k_{x})^{2}+(\pm A_{ M}+\tau _{z}A_{S})^{2}}\), waarbij het ± teken overeenkomt met de P- en AP-configuratie van magnetisaties. Dus alleen \(K^{^{\prime }}\) elektronen worden gedetecteerd in de P-structuur en alleen K elektronen worden gedetecteerd in de AP-structuur wanneer de Fermi-energie zich in het bereik van [|A bevindt M −A S |,A M +A S ]. In het grafeenkanaal is het dal degenereren ook lift, maar er is een belangrijk verschil. In tegenstelling tot het hoofdgeval, waar de fasen van K en \(K^{^{\prime }}\) componenten evolueren met dezelfde golfvector [dwz, \(k=E/\hbar v_{F}\)], nu evolueren ze afzonderlijk met verschillende golfvectoren ( \(k_{+}=(EU)/(\hbar v_{F}+\hbar v_{\tau })\) en \(k_{-}=(EU)/(\hbar v_{F}-\ hbar v_{\tau })\)) vanwege de Kek-Y grafeen superroosters die de vallei vermengen (zie vergelijking 2). Dit leidt tot de dalprecessie van kanaalelektronen in de dalruimte [12]. De vallei-precessie in grafeen is de basis voor de vallei-veldeffecttransistor [8]. En de vallei-precessie kan ook worden gekenmerkt door een vallei-pseudomagnetoweerstand (VPMR) in de FM-S/Kek-Y/FM-S-overgangen, analoog aan de magnetoweerstand in op grafeen gebaseerde kwantumtunneling-overgangen met de spin-baaninteractie [4] , die is gedefinieerd als \(VPMR=\frac {G_{P}-G_{AP}}{G_{P}}\), waarbij G P en G AP vertegenwoordigen de conductantie in respectievelijk P- en AP-configuraties, en \(G_{P}=G_{K^{^{\prime }},K^{^{\prime }}}, G_{AP}=G_{K ^{^{\prime }},K}\). De grootte van de dalstroom hangt af van de magnetische oriëntatie van de source en drain in ons beschouwde apparaat.

Numerieke resultaten en discussies

Hieronder presenteren we de numerieke resultaten voor de FM-S/Kek-Y/FM-S-junctie in grafeen. Door de hele krant heen stellen we de kanaallengte L . in =207nm, en beperk de Fermi-energie 20 meV<E <140meV, aangenomen dat het voldoet aan |A M −A S |<E <A M +A S . Figuur 2a en b tonen de berekende resultaten van tunnelgeleiding en VPMR als functie van v t met Fermi-energie E =80meV en rechthoekige potentiaalbarrière U =−10meV. We kunnen vinden dat G P en G AP hebben dezelfde oscillatieperioden maar de inverse fasen. Daarom oscilleert de VPMR met een toename van v t en de negatieve waarde VPMR kan verschijnen. Die verschijnselen zijn vergelijkbaar met het geval van de magnetoweerstand in op ballistische grafeen gebaseerde kwantumtunneling-overgangen met de spin-baaninteractie [4]. De oscillatiekarakters van de conductantie van G P en G AP kan worden verklaard door het faseverschil tussen de twee valleicomponenten. Wanneer de invalshoek ϕ 0 =0, de faseverschuiving wordt gegeven door:\(\Delta \theta =(k_{x+}-k_{x-})L=-\frac {2(EU)v_{\tau }}{\hbar (v_ {F}^{2}-v_{\tau }^{2})}L\). Δ θ bepaalt de oriëntatie van de dalpolarisatie voordat het elektron de afvoer binnengaat, ten opzichte van die van de afvoertoestand [8]. Voor Δ θ =±2n π ,n =1,2,3⋯, de twee polarisaties zijn uitgelijnd, wat leidt tot de conductantie G P maximum en VPMR een hoge positieve waarde (zoals te zien in v τ =0,022, 0,033). Aan de andere kant, voor Δ θ =±(2n +1)π ,n =0,1,2⋯, ze staan ​​loodrecht op elkaar, wat leidt tot de conductantie G AP minimum en VPMR-negatief (zoals te zien in v τ =0,0167, 0,027, 0,038).

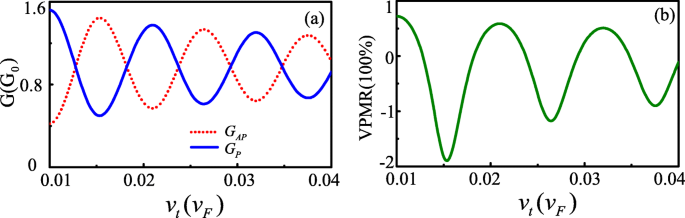
Geleiding G P ,A P en VPMR versus v t bij L =207nm,E =80meV en U =−10meV (kleur online)

De conductantie en VPMR zijn niet alleen oscillatiefuncties van de hopping-energiemodificatie, ze oscilleren ook met Fermi-energie en het effectieve barrièrepotentieel sinds Δ θ schalen zijn ook lineair met de Fermi-energie en de potentiële barrière U . Figuur 3a en b tonen respectievelijk de conductantie als functie van Fermi-energie en het effectieve barrièrepotentieel. De overeenkomstige VPMR worden gegeven in Fig. 3c en d. Ze vertonen allemaal oscillatiekarakteristieken die variëren met E en U waarde, zelfs wanneer het effectieve barrièrepotentieel U is groter dan Fermi-energie E . De fysieke oorsprong van een dergelijk fenomeen is gerelateerd aan de Klein tunneling [12]. Hoewel er vergelijkbare oscillatieverschijnselen van geleiding en VPMR zijn voor verhoogde E en U , zijn er ook enkele verschillen te vinden. Als E toeneemt, wordt het verschil tussen G P en G AP geleiding wordt kleiner en kleiner, wat ertoe leidt dat de oscillatie-amplitude van VPMR afneemt met de toename van Fermi-energie. Terwijl onder de voorwaarde Δ θ =±n π is voldaan, het verschil tussen G P en G AP is groter naarmate U . toeneemt , vooral op sommige plaatsen, de G P en G AP geleidbaarheid presenteert schakelkarakteristieken. De karakters zijn meer wenselijk voor de toepassing van VPMR. Opmerkelijk is dat de waargenomen maximale waarde van VPMR meer dan 30.000% is bij kleine E . Deze waarde is veel groter dan de MR van ~ 175% in de op ballistische grafeen gebaseerde kwantumtunneling-overgangen met de spin-baaninteractie [4] en de pseudomagnetoweerstand van ~ 100% in dubbellaags grafeen gecontroleerd door externe poorten [24], wat zelfs groter is dan de VPMR van ~ 10000% in een samenvoegend Dirac-kegelsysteem [13].

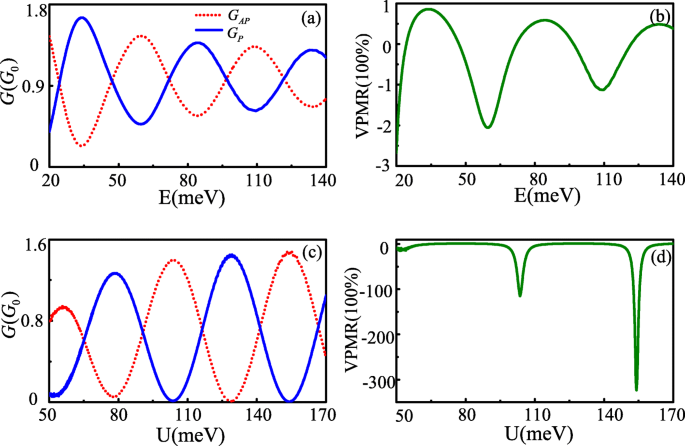
Geleiding G P ,A P (een , c ) en VPMR (b , d ) als functies van de Fermi-energie en de elektrische barrière bij L =207nm,v t =0.02v f . de andere parameters zijn U =−10meV voor a en c , E =80meV voor b en d (kleur online)

Conclusies

Concluderend hebben we een type vallei-veldeffecttransistors voor op grafeen gebaseerd elektron voorgesteld en de pseudomagnetoweerstand van de vallei erdoorheen bestudeerd. We hebben aangetoond dat de oscillatie-eigenschap van pseudomagnetoweerstand van de vallei niet alleen gerelateerd is aan de hopping-energiemodificatie en Fermi-energie, maar ook grotendeels kan worden afgestemd door het effectieve barrièrepotentieel. De vallei pseudomagnetoweerstand afgestemd door externe voorspanning komt de vallei-veldeffecttransistorinrichting ten goede, en we verwachten dat de elektrisch gestuurde valleikwantumapparaten die hier worden voorgesteld een rol kunnen spelen in kwantum- en kwantumklassieke hybride computers.

Verder onderzoek kan betrekking hebben op de verschillende spanning (uniaxiaal versus biaxiaal) die de valleiverstrooiing van elektronen en transport in onze voorgestelde op grafeen gebaseerde vallei-veldeffecttransistoren afstemt, aangezien de vlek nuttig is om de mate van intervalverstrooiing in Kekulé-patronen te regelen [25] . Dan, andere tweedimensionale materialen (MoS2 , WS2 , WSe2 , etc.) analogen in grafeen kunnen ook een interessant platform bieden voor andere tweedimensionale, op materiaal gebaseerde vallei-veldeffecttransistoren met Y-vormige Kekulé-roostervervorming.

Beschikbaarheid van gegevens en materialen

De datasets die de conclusies van dit artikel ondersteunen, zijn in het artikel opgenomen.

Afkortingen

AP:

Antiparallel

FM-S:

Ferromagnetische spanning

Kek-Y:

Y-vormige Kekulé

P:

Parallel

VFET's:

Valley-veldeffecttransistors

VPMR:

Vallei pseudomagnetoweerstand


Nanomaterialen

  • Metaal
  • Hars
  • vezel
  • Samengesteld materiaal
  • Nanomaterialen
  • Polymeer materialen
  • Biologie
  • kleurstof
  • Kruiden
    1. Lattice:MachX03D FPGA verbetert de beveiliging met hardware root-of-trust-mogelijkheden
    2. Grafeen zet nanomaterialen op hun plaats
    3. Grafeen in luidsprekers en oortelefoons
    4. Grafeen nanolint
    5. RGO en driedimensionale grafeennetwerken hebben TIM's samen gemodificeerd met hoge prestaties
    6. Evaluatie van grafeen/WO3 en grafeen/CeO x-structuren als elektroden voor supercondensatortoepassingen
    7. Grafeen/polyaniline-aerogel met superelasticiteit en hoge capaciteit als zeer compressietolerante supercondensatorelektrode
    8. Milieuvriendelijke en gemakkelijke synthese van Co3O4-nanodraden en hun veelbelovende toepassing met grafeen in lithium-ionbatterijen
    9. Op grafeenoxide gebaseerde nanocomposieten versierd met zilveren nanodeeltjes als antibacterieel middel
    10. Voorbereiding van ultrahoog moleculair gewicht polyethyleen/grafeen nanocomposiet in situ polymerisatie via sferische en sandwichstructuur grafeen/Sio2 ondersteuning
    11. Hoog-efficiënte plasmonische derde-harmonische generatie met grafeen op een siliciumdiffractief rooster in het midden-infraroodgebied