Door elektrisch veld gecontroleerde indirecte-direct-indirecte bandgap-overgang in monolaag InSe

Abstract

Elektronische structuren van monolaag InSe met een loodrecht elektrisch veld worden onderzocht. Indirect-direct-indirecte bandgap-overgang wordt gevonden in monolaag InSe omdat de elektrische veldsterkte continu wordt verhoogd. Ondertussen wordt de wereldwijde bandgap geleidelijk tot nul onderdrukt, wat aangeeft dat halfgeleider-metaaltransformatie plaatsvindt. De onderliggende mechanismen worden onthuld door zowel de orbitale bijdragen aan de energieband als de evolutie van bandranden te analyseren. Deze bevindingen vergemakkelijken niet alleen ons verder begrip van elektronische kenmerken van gelaagde groep III-VI halfgeleiders, maar bieden ook nuttige richtlijnen voor het ontwerpen van opto-elektronische apparaten.

Inleiding

Sinds het baanbrekende werk aan de experimentele realisatie van een enkellaags grafiet, namelijk grafeen [1, 2], is er veel aandacht besteed aan atomair dunne tweedimensionale (2D) materialen [3, 4]. Verschillende monolaag 2D-materialen zijn theoretisch voorspeld of experimenteel ontdekt, waaronder siliceen [5-7], germanaan [8], zwarte fosfor [9, 10], overgangsmetaal dichalcogeniden (TMD's) [11-13] en hexagonaal boornitride [14 –16]. Hoewel deze atomair dunne 2D-materialen dezelfde honingraatstructuur hebben, zijn hun elektronische structuren en geleidbaarheidseigenschappen behoorlijk verschillend, waaronder metaal [1, 2, 5-8], halfgeleider [9-13] en isolator [14-16]. Daarom kunnen deze enkellaagse 2D-materialen, volgens hun elektronische karakters, toepassingen vinden in het ontwerp van multifunctionele elektronische en optische apparaten [3, 4]. Bijvoorbeeld afstembare optische apparaten met een hoogwaardige factor op basis van Si-grafeen-metamaterialen [17], Cu-grafeen-metamaterialen [18] en MoS₂ -SiO₂ -Si golfgeleiderstructuren [19] worden voorgesteld. Perfecte vallei en/of spin polarisatie apparaten op basis van het ferromagnetische grafeen [20], gespannen grafeen met Rashba spin-orbit koppeling en magnetische barrière [21], en gespannen siliceen met een elektrisch veld worden gesuggereerd [22, 23]. Bovendien zijn de interactie-effecten tussen de ontledingscomponenten van SF₆ en verschillende materialen, waaronder N-gedoteerde enkelwandige koolstofnanobuizen [24], Pt₃ -TiO₂ (1 0 1) oppervlak [25], Ni-gedoteerde MoS₂ monolaag [26] en Pd (1 1 1) oppervlak [27] worden onderzocht met behulp van de dichtheidsfunctionaaltheorie (DFT).

Groep III-VI-verbindingen MX's (M =Ga, In en X =S, Se, Te) zijn een andere familie van gelaagde 2D-materialen. Vanwege hun unieke elektrische karakter hebben deze materialen de aandacht van veel onderzoekers getrokken [28]. DFT [29–33] en nauwsluitende modelberekeningen [34] laten zien dat de energiebandafstand van gelaagde MX's afhankelijk is van de dikte en toeneemt van 1,3 tot 3,0 eV naarmate het aantal lagen afneemt. Tegelijkertijd wordt een direct-indirecte bandgap-overgang waargenomen, die tegengesteld is aan het gedrag van gelaagde zwarte fosfor [9, 10] en TMD's [11–13]. Deze aanzienlijke energiebandgapmodulatie van gelaagde MX's kan worden gebruikt om opto-elektronische apparaten te ontwerpen [35, 36]. Daarnaast is de stabiliteit van InSe gedoteerd met zuurstofgebreken onderzocht en is gevonden dat het stabieler is dan zwarte fosfor in de lucht [37]. Het magnetisme van de InSe-monolaag kan worden afgesteld door As [38], C en F [39] te adsorberen. Een enorm spin-lading conversie-effect wordt gevonden in dubbellaags InSe vanwege de gebroken spiegelsymmetrie [40]. Bovendien zijn de elektronische structuur en de stroom-spanningskarakteristieken van monolaag InSe-nanoribbons sterk afhankelijk van de randtoestanden [41]. Aan de andere kant verifiëren experimentele onderzoeken de laagafhankelijke elektronische structuren van MX's en kunnen ze reageren op het licht dat de zichtbare en nabij-infrarode gebieden overspant [42–45]. Ook blijkt de draaggolfmobiliteit van MX's hoog te zijn, waardoor ze kunnen worden gebruikt om veldeffecttransistoren te ontwerpen. Voor bulk GaS en GaSe zijn de draaggolfmobiliteiten ongeveer 80 en 215 cm ² V ⁻¹ S ⁻¹ [46], respectievelijk. Voor de monolaag InSe is de mobiliteit van de drager zelfs tot bijna 10 ³ cm ² V ⁻¹ S ⁻¹ [47]. Bovendien kan de band gap van gelaagd InSe worden gemanipuleerd door uniaxiale trekspanning, die wordt geïdentificeerd door de fotoluminescentiespectra [48].

Vanuit het oogpunt van het ontwerp van opto-elektronische apparaten is de efficiëntie van de apparaten op basis van directe bandgap-halfgeleiders beter dan die op basis van indirecte bandgap-halfgeleiders. Daarom is het transformeren van indirecte bandgap-mx's met een paar lagen naar het directe bandgaptype een uitdaging voor de wetenschappelijke gemeenschap. Zeer recent zijn bandgapmanipulatie en indirect-directe bandgapovergang gevonden in monolaag InSe door uniaxiale rek [49]. Ook zijn directe band gap halfgeleiders verkregen door 2D n-InSe en p-GeSe(SnS) te stapelen. En de band gap-waarden en bandoffset van deze van der Waals-heterojuncties kunnen worden afgestemd door de tussenlaagkoppeling en het externe elektrische veld [50]. Daarnaast worden de mogelijke stapelconfiguraties van dubbellaags InSe en de invloed van het loodrechte elektrische veld op hun elektronische structuren bestudeerd. Indirecte bandgap dubbellaags InSe kan worden getransformeerd naar het metallische type door de elektrische veldsterkte te variëren [51]. Evenzo wordt in andere geknikte 2D-materialen zoals siliceen [52], germaneen [53], overgangsmetaaldichalcogeniden [54, 55] en zwarte fosfor [56] ook een loodrecht elektrisch veld voorgesteld om hun bandafstand en elektronische kenmerken af te stemmen. In het licht van deze eerdere studies kan een natuurlijke vraag worden gesteld wat de elektrische veldeffecten zijn op de elektronische structuren van de monolaag InSe.

In deze brief worden de effecten van een loodrecht elektrisch veld op de elektronische structuren van de monolaag InSe onderzocht met behulp van het nauw bindende model Hamiltoniaan. Indirecte-direct-indirecte bandgap-overgang kan worden bereikt in het beschouwde systeem met toenemende elektrische veldsterkte. Tegelijkertijd wordt de bandafstand van de monolaag InSe geleidelijk kleiner, waardoor deze uiteindelijk metaalachtig wordt. De onderliggende natuurkundige mechanismen van deze effecten worden ontrafeld door de orbitale decompositie voor de energieband en de elektrisch veld-gemoduleerde energiepositieverschuiving van de bandranden te analyseren. Onze studies kunnen er baat bij hebben om de elektronische eigenschappen van InSe met weinig lagen fundamenteel te begrijpen en om theoretische basis te bieden voor 2D opto-elektronische apparaten.

Methoden

Het bovenaanzicht van de InSe-monolaag is geschetst in figuur 1a, waar de grote paarse bollen indiumionen voorstellen, terwijl de kleine groene seleniumionen weergeven. Deze twee soorten ionen vormen een grafeenachtige hexagonale structuur in de xy vlak met roosterconstante a , de afstand tussen de dichtstbijzijnde In- of Se-ionen. Figuur 1b toont het schematische zijaanzicht van de InSe-monolaag. Verschillend van grafeen, twee sublagen met spiegelsymmetrie in de xz vliegtuig worden waargenomen. De verticale afstand tussen In (Se)-ionen van verschillende sublagen is ingesteld op d (D ). Daarom bestaat een eenheidscel van monolaag InSe uit vier ionen S e ₁ , ik n ₁ , S e ₂ , en ik n ₂ , zoals weergegeven door de rode ellips in Fig. 1b, waarbij nummer 1 (2) de sublaagindex aangeeft.

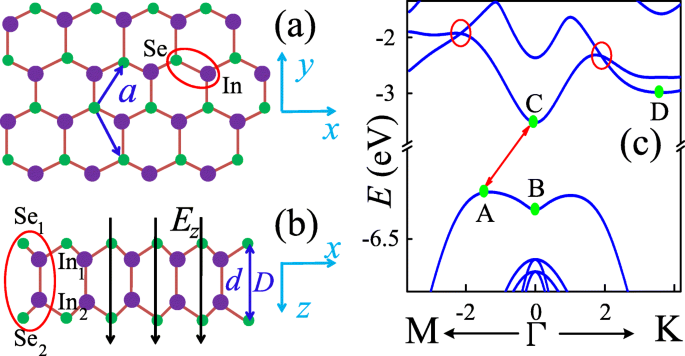
(Online kleuren) Boven (a ) en zijkant (b ) weergave van de monolaag InSe in de xy en xz vliegtuigen resp. De roosterconstante tussen de dichtstbijzijnde In- of Se-ionen in de xy vliegtuig is een , en de afstand tussen de dichtstbijzijnde In (Se) -ionen in verschillende sublagen is d (D ). Een loodrecht elektrisch veld langs z -as E _z wordt aangebracht op de monolaag InSe. c Energieband van monolaag InSe

De hechte Hamiltoniaan tot de op één na dichtstbijzijnde buurinteracties inclusief alle mogelijke sprongen tussen de s en p orbitalen van In en Se ionen leest [34]

$$ H=\sum\limits_{l} H_{0l}+H_{ll}+H_{ll'}, $$ (1)

waarbij de som loopt over de sublagen l =1 en 2, en l ^′ =2(1) als l =1(2). H _0l , H _zal , en $\phantom {\dot {i}\!}H_{ll^{\prime }}$ bestaan uit termen die afkomstig zijn van de on-site energieën, respectievelijk hoppende energieën binnen en tussen de twee sublagen. En de expliciete uitdrukkingen ervan worden gegeven als [34]

$$\begin{array}{@{}rcl@{}} H_{0l}=\sum\limits_{i}[\varepsilon_{\text{In}_{s}}a_{lis}^{\dag }a_{lis}+ \sum\limits_{\alpha}\varepsilon_{\text{In}_{p_{\alpha}}}a_{{lip}_{\alpha}}^{\dag}a_{{ lip}_{\alpha}}+ \\ \varepsilon_{\text{Se}_{s}}b_{lis}^{\dag}b_{lis}+ \sum\limits_{\alpha}\varepsilon_{\ text{Se}_{p_{\alpha}}}b_{{lip}_{\alpha}}^{\dag}b_{{lip}_{\alpha}}], \end{array} $$ ( 2)

waarbij de som loopt over alle eenheidscellen in sublaag l . $\phantom {\dot {i}\!}\varepsilon _{\mathrm {In(Se)}_{s}}$ is de on-site energie voor de s orbitaal van In (Se) ionen, terwijl $\phantom {\dot {i}\!}\varepsilon _{\mathrm {In(Se)}_{p_{\alpha }}}$ dat is voor orbitaal p _α (α =x ,j ,z ). $a_{lis}^{\dag }$ (a _lis ) is de creatie (annihilatie) operator voor een elektron in s orbitaal op In-ionen in eenheidscel i en sublaag l , maar $\phantom {\dot {i}\!}a_{{lip}_{\alpha }}^{\dag }$ ($\phantom {\dot {i}\!}a_{{ lip}_{\alpha }}$) voor een elektron in p _α orbitaal. Evenzo, b ^† (b ) is de creatie (annihilatie) operator voor een elektron in de relevante orbitaal op Se ionen.

$$\begin{array}{@{}rcl@{}} H_{ll}=H_{ll}^{(\text{In}-\text{Se})_{1}}+H_{ll} ^{\text{In}-\text{In}}+H_{ll}^{\text{Se}-\text{Se}}+H_{ll}^{(\text{In}-\text{ Se})_{2}}, \end{array} $$ (3)

waarin [34]

$$ {{}{\begin{aligned} H_{ll}^{(\text{In}-\text{Se})_{1}}=\sum\limits_{<\text{In}_{li },\text{Se}_{lj}>}\{T_{ss}^{(\text{In}-\text{Se})_{1}}b_{ljs}^{\dag} a_{ lis}+T_{sp}^{(\text{In}-\text{Se})_{1}}\sum\limits_{\alpha}R_{\alpha}^{\text{In}_{li }\text{Se}_{lj}} \\ b_{ljp_{\alpha}}^{\dag} a_{lis}+T_{ps}^{(\text{In}-\text{Se}) _{1}}\sum\limits_{\alpha}R_{\alpha}^{\text{In}_{li}\text{Se}_{lj}}b_{ljs}^{\dag} a_{ lip_{\alpha}}+\sum\limits_{\alpha,\beta}\{[\delta_{\alpha\beta}T_{\pi}^{(\text{In}-\text{Se})_ {1}}- \\ (T_{\pi}^{(\text{In}-\text{Se})_{1}}+T_{\sigma}^{(\text{In}-\text {Se})_{1}})R_{\alpha}^{\text{In}_{li}\text{Se}_{lj}} R_{\beta}^{\text{In}_{ li}\text{Se}_{lj}}]b_{ljp_{\beta}}^{\dag} a_{lip_{\alpha}}\}\}+\mathrm{Hc}, \end{aligned} }} $$ (4) $$ { \begin{aligned} H_{ll}^{\text{In}-\text{In}}=\sum\limits_{<\text{In}_{li}, \text{In}_{lj}>}\{T_{ss}^{\text{In}-\text{In}}a_{ljs}^{\dag} a_{lis}+T_{sp}^ {\text{In}-\text{In}}\sum\limits_{\alpha}R_{\alpha}^{\text{In}_{li}\text{In}_{lj}} a_{ljp_ {\een lpha}}^{\dag} a_{lis}+ \\ \sum\limits_{\alpha,\beta}\{[\delta_{\alpha\beta}T_{\pi}^{\text{In}- \text{In}}- (T_{\pi}^{\text{In}-\text{In}}+T_{\sigma}^{\text{In}-\text{In}})R_{ \alpha}^{\text{In}_{li}\text{In}_{lj}} R_{\beta}^{\text{In}_{li}\text{In}_{lj}} ]a_{ljp_{\beta}}^{\dag} a_{lip_{\alpha}}\}\} \\ +\mathrm{Hc}, \end{aligned}} $$ (5) $$ { \ begin{aligned} H_{ll}^{\text{Se}-\text{Se}}=\sum\limits_{<\text{Se}_{li},\text{Se}_{lj}>} \{T_{ss}^{\text{Se}-\text{Se}}b_{ljs}^{\dag} b_{lis}+T_{sp}^{\text{Se}-\text{Se }}\sum\limits_{\alpha}R_{\alpha}^{\text{Se}_{li}\text{Se}_{lj}} b_{ljp_{\alpha}}^{\dag} b_ {lis}+ \\ \sum\limits_{\alpha,\beta}\{[\delta_{\alpha\beta}T_{\pi}^{\text{Se}-\text{Se}}- (T_ {\pi}^{\text{Se}-\text{Se}}+T_{\sigma}^{\text{Se}-\text{Se}})R_{\alpha}^{\text{Se }_{li}\text{Se}_{lj}} R_{\beta}^{\text{Se}_{li}\text{Se}_{lj}}]b_{ljp_{\beta}} ^{\dag} b_{lip_{\alpha}}\}\} \\ +\mathrm{Hc}, \end{aligned}} $$ (6)

$$ { \begin{aligned} H_{ll}^{(\text{In}-\text{Se})_{2}}=\sum\limits_{<\text{In}_{li},\ text{Se}_{lj'}>}\{T_{ss}^{(\text{In}-\text{Se})_{2}}b_{lj's}^{\dag} a_{lis} +T_{sp}^{(\text{In}-\text{Se})_{2}}\sum\limits_{\alpha}R_{\alpha}^{\text{In}_{li}\ text{Se}_{lj'}} \\ b_{lj'p_{\alpha}}^{\dag} a_{lis}+T_{ps}^{(\text{In}-\text{Se} )_{2}}\sum\limits_{\alpha}R_{\alpha}^{\text{In}_{li}\text{Se}_{lj'}}b_{lj's}^{\dag} a_{lip_{\alpha}}+\sum\limits_{\alpha,\beta}\{[\delta_{\alpha\beta}T_{\pi}^{(\text{In}-\text{Se} )_{2}}- \\ (T_{\pi}^{(\text{In}-\text{Se})_{2}}+T_{\sigma}^{(\text{In}- \text{Se})_{2}})R_{\alpha}^{\text{In}_{li}\text{Se}_{lj'}} R_{\beta}^{\text{In }_{li}\text{Se}_{lj'}}]b_{lj'p_{\beta}}^{\dag} a_{lip_{\alpha}}\}\}+\mathrm{Hc} \end{uitgelijnd}} $$ (7)

de hopping-termen opnemen tussen de dichtstbijzijnde In-Se-, In-In-, Se-Se- en de volgende dichtstbijzijnde In-Se-paren binnen dezelfde sublaag l , respectievelijk. $T_{ss/sp/ps}^{\mathrm {X}}$ is de hopping-integraal voor de ss /sp /ps orbitalen tussen het corresponderende paar X, terwijl $T_{\pi (\sigma)}^{\mathrm {X}}$ dat is voor de parallelle p en p orbitalen loodrecht op (liggend langs) de huppelvector $R_{\alpha }^{\mathrm {X}}$ [57]. Bijvoorbeeld

$$\begin{array}{@{}rcl@{}} R_{\alpha}^{(\text{In}-\text{Se})_{1}}=\frac{\mathrm{\mathbf {R}}_{\text{Se}_{lj}}-\mathrm{\mathbf{R}}_{\text{In}_{li}}} {|\mathrm{\mathbf{R}} _{\text{Se}_{lj}}-\mathrm{\mathbf{R}}_{\text{In}_{li}}|}\cdot \hat{\alpha}, \end{array} $$ (8)

waarbij $\phantom {\dot {i}\!}\mathrm {\mathbf {R}}_{{\text {In}_{li}}/{\text {Se}_{lj}}}\ ) is de positievector voor In_li /Se_lj , \(\hat {\mathbf {\alpha }}$ is een eenheidsvector langs α .

$$\begin{array}{@{}rcl@{}} H_{ll'}=H_{ll'}^{(\text{In}-\text{In})_{1}}+H_{ ll'}^{\text{In}-\text{Se}}+H_{ll'}^{(\text{In}-\text{In})_{2}}, \end{array} $ $ (9)

waarin [34]

$$ { \begin{aligned} H_{ll'}^{({\text{In}-\text{In}})_{1}}=\sum\limits_{i}\{T_{ss}^ {({\text{In}-\text{In}})_{1}}a_{l'is}^{\dag} a_{lis}+T_{sp}^{({\text{In} -\text{In}})_{1}}\sum\limits_{\alpha}R_{\alpha}^{\text{In}_{li}\text{In}_{l'i}} a_ {l'ip_{\alpha}}^{\dag} a_{lis}+ \\ \sum\limits_{\alpha,\beta}\{[\delta_{\alpha\beta}T_{\pi}^{ ({\text{In}-\text{In}})_{1}}- (T_{\pi}^{({\text{In}-\text{In}})_{1}}+ T_{\sigma}^{({\text{In}-\text{In}})_{1}})R_{\alpha}^{\text{In}_{li}\text{In}_ {l'i}} R_{\beta}^{\text{In}_{li}\text{In}_{l'i}}] \\ a_{l'ip_{\beta}}^{\ dag} a_{lip_{\alpha}}\}\}+\mathrm{Hc}, \end{aligned}} $$ (10) $$ { \begin{aligned} H_{ll'}^{\text{ In}-\text{Se}}=\sum\limits_{<\text{In}_{li},\text{Se}_{l'j}>}\{T_{ss}^{\text{ In}-\text{Se}}b_{l'js}^{\dag} a_{lis}+T_{sp}^{\text{In}-\text{Se}}\sum\limits_{\alpha }R_{\alpha}^{\text{In}_{li}\text{Se}_{l'j}} \\ b_{l'jp_{\alpha}}^{\dag} a_{lis} +T_{ps}^{\text{In}-\text{Se}}\sum\limits_{\alpha}R_{\alpha}^{\text{In}_{li}\text{Se}_{ l'j}}b_{l'js}^{\dag} a_ {lip_{\alpha}}+\sum\limits_{\alpha,\beta}\{[\delta_{\alpha\beta}T_{\pi}^{\text{In}-\text{Se}}- \\ (T_{\pi}^{\text{In}-\text{Se}}+T_{\sigma}^{\text{In}-\text{Se}})R_{\alpha}^{ \text{In}_{li}\text{Se}_{l'j}} R_{\beta}^{\text{In}_{li}\text{Se}_{l'j}}] b_{l'jp_{\beta}}^{\dag} a_{lip_{\alpha}}\}\}+\mathrm{Hc}, \end{aligned}} $$ (11)

$$ { \begin{aligned} H_{ll'}^{({\text{In}-\text{In}})_{2}}=\sum\limits_{i}\{T_{ss}^ {({\text{In}-\text{In}})_{2}}a_{l'js}^{\dag} a_{lis}+T_{sp}^{({\text{In} -\text{In}})_{2}}\sum\limits_{\alpha}R_{\alpha}^{\text{In}_{li}\text{In}_{l'j}} a_ {l'jp_{\alpha}}^{\dag} a_{lis}+\\ \sum\limits_{\alpha,\beta}\{[\delta_{\alpha\beta}T_{\pi}^{ ({\text{In}-\text{In}})_{2}}- (T_{\pi}^{({\text{In}-\text{In}})_{2}}+ T_{\sigma}^{({\text{In}-\text{In}})_{2}})R_{\alpha}^{\text{In}_{li}\text{In}_ {l'j}} R_{\beta}^{\text{In}_{li}\text{In}_{l'j}}] \\ a_{l'jp_{\beta}}^{\ dag} a_{lip_{\alpha}}\}\}+\mathrm{Hc} \end{aligned}} $$ (12)

omvatten de hopping-termen tussen de dichtstbijzijnde In-In, In-Se en volgende dichtstbijzijnde In-In-paren tussen sublagen l en l ^′ , respectievelijk. Als een loodrecht elektrisch veld langs z -as wordt toegepast op de monolaag InSe, de effecten ervan kunnen worden geïntroduceerd door een wijziging van de on-site orbtiële energieën van In- en Se-ionen, dat wil zeggen

$$\begin{array}{@{}rcl@{}} \varepsilon'=\varepsilon+eE_{z}z, \end{array} $$ (13)

waar e is de elektronenlading en E _z is de sterkte van het loodrechte elektrische veld. Het loodrechte elektrische veld kan worden bereikt door boven- en onderpoorten toe te voegen aan de monolaag InSe. Bovendien zijn er twee isolerende lagen tussen de monolaag InSe en poorten geplaatst om de elektrische stroom langs z te elimineren -as. Als resultaat kan de elektrische veldsterkte worden afgestemd door de poortspanning te variëren.

Door de strak bindende Hamiltoniaan in Vgl. (1) in de k ruimte en vervolgens diagonaliseren, energiebanden E (k ) van monolaag InSe zonder of met een loodrecht elektrisch veld kan gemakkelijk worden verkregen, waarbij k is golfvector. Tegelijkertijd is de coëfficiënt van eigenvector C _{n k} (o ) bij band n , orbitaal o , en golfvector k kan ook worden bereikt.

Numerieke resultaten en discussies

De roosterparameters van monolaag InSe in Fig. 1a en b worden genomen als a =3.953 Å, d =2,741 Å, en D =5,298 Å, die worden verkregen door de lokale dichtheidsbenadering [30]. De on-site en hoppende energieën in de strak bindende Hamiltonian Eq. (1) worden gegeven in tabel 1, die zijn aangepast door de gegevens van de dichtheidsfunctionaaltheorie met schaarcorrectie [34]. Hoewel hier alleen de numerieke resultaten van de monolaag InSe worden gegeven, zijn kwalitatief vergelijkbare resultaten ook gevonden in de dubbellaagse InSe en de bulk InSe. Voor de beknoptheid worden ze in deze brief niet gepresenteerd.

Figuur 1c toont de energieband van de monolaag InSe. De geleidingsbanden rond punt Γ vertonen parabool-achtige energiedispersie, die vergelijkbaar is met die van andere normale halfgeleiders. De bandstructuur langs Γ−K is echter enigszins asymmetrisch met die langs Γ−M. En de onderste twee geleidingsbanden die elkaar kruisen in beide richtingen, zoals aangegeven door de rode cycli. In tegenstelling tot de geleidingsbanden, is de hoogste valentieband vlak maar enigszins omgekeerd rond punt Γ, wat een interessante Mexicaanse hoedachtige structuur vormt. Daarom is monolaag InSe een indirecte bandgap-halfgeleider, die behoorlijk verschilt van die van bulk-InSe, omdat het een directe bandgap-halfgeleider is. De energiekloof van monolaag InSe kan worden verkregen door $E_{\mathrm {g}}^{\text {id}}=E_{\mathrm {C}}-E_{\mathrm {A}}=2.715$ eV, die veel is vergroot door vergelijking met die van bulk InSe $E_{\mathrm {g}}^{\mathrm {d}}=1.27$ eV [34]. De andere valentiebanden vertonen echter een normale parabool-achtige energiespreiding.

Om de energieband van monolaag InSe weergegeven in Fig. 1c te begrijpen, de orbitale decompositie |C _{n k} (o )|² voor de energieband wordt gegeven in Fig. 2. Aangezien de twee sublagen van de monolaag InSe symmetrisch is langs z -as hebben de ionen in verschillende sublagen dezelfde orbitale bijdragen aan de energieband. Hier worden In- en Se-ionen in sublaag 2, zoals weergegeven in figuur 1b, als voorbeelden genomen. De bovenste panelen geven orbitale bijdragen van In-ionen aan, terwijl de onderste panelen die van Se-ionen vertegenwoordigen. De dikte van lijnen is evenredig met de genormaliseerde orbitale bijdrage. Het is te zien dat de laagste geleidingsband rond punt Γ eerst wordt bijgedragen door p _z orbitaal van Se ion en dan s orbitaal van In ion. De tweede geleidingsband rond K-punt is dominant afkomstig van p _x orbitaal van In ion en dan p _z orbitaal van Se ion. De hoogste valentieband wordt echter voornamelijk bijgedragen door p _z orbitaal van Se ion. De andere valentiebanden zijn het resultaat van beide p _x en p _j orbitalen van Se ion. Deze resultaten komen overeen met de resultaten die zijn verkregen door de DFT-berekeningen [34].

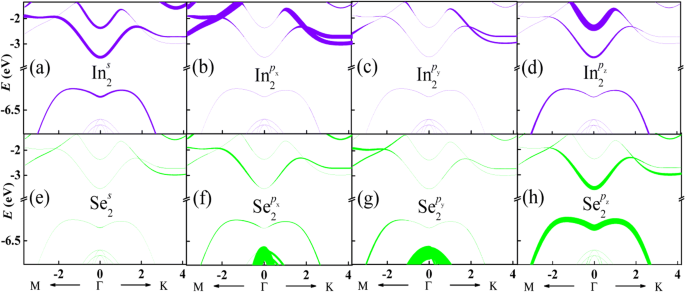
(Kleur online) Orbitale decomposities voor de energieband van monolaag InSe. Dikkere lijnen duiden op een meer dominante bijdrage. Alleen In- en Se-ionen in sublaag 2 worden als voorbeelden geselecteerd, aangezien de twee sublagen van de monolaag InSe met spiegelsymmetrie langs z -as (a –u )

Energieband van de monolaag InSe met een loodrecht elektrisch veld langs z -as wordt getoond in Fig. 3a. De elektrische veldsterkte wordt genomen als E _z =2,0 V/nm. Door te vergelijken met de energieband in figuur 1c, wordt elke geleidings- en valentieband opgeheven naar het hogere energiegebied als geheel. De energieverschuiving van elke band is echter anders omdat de orbitale decompositie van de p _z orbitaal van In en Se ionen is anders. De positie van de maximale waarde van de hoogste valentieband wordt gewijzigd in punt Γ, terwijl die van de minimumwaarde van de geleidingsband ongewijzigd blijft. Daarom wordt de monolaag InSe getransformeerd in een directe bandgap halfgeleider. En de energiekloof wordt verkleind tot $E_{\mathrm {g}}^{\mathrm {d}}=2.61$ eV. Verder worden de kruisingen langs zowel Γ−K- als Γ−M-richtingen geopend zodat energiekloven worden gegenereerd, zoals weergegeven door de rode cycli, aangezien de symmetrie langs z -as wordt onderbroken door het loodrechte elektrische veld. Wanneer de elektrische veldsterkte wordt verhoogd tot E _z =6,0 V/nm, wordt de energiekloof op punt Γ kleiner, maar die op de kruispunten wordt verder vergroot, zoals weergegeven in figuur 3b. Interessant is dat de positie van de minimale waarde van de geleidingsband verandert van punt Γ naar die rond punt K, terwijl die van de maximale waarde van de hoogste valentieband op punt blijft. Dit fenomeen betekent dat de monolaag InSe opnieuw wordt getransiteerd in indirecte bandgap halfgeleider en de indirecte energiekloof van de hele band $E_{\mathrm {g}}^{\text {id}}=1.30$ eV. Evenzo kan de band gap van monolaag InSe worden gecontroleerd door biaxiale spanning. De band gap varieert van 1.466 tot 1.040 eV wanneer de spanning wordt gevarieerd van 1 tot 4%. Bovendien wordt een indirecte-directe bandgapovergang ook waargenomen wanneer de monolaag InSe onder uniaxiale spanning staat [49]. Voor de dubbellaagse InSe met een loodrecht elektrisch veld, neemt de bandafstand af naarmate de elektrische veldsterkte toeneemt en wordt deze gesloten wanneer de elektrische veldsterkte wordt verhoogd tot 2,9 V/nm [51].

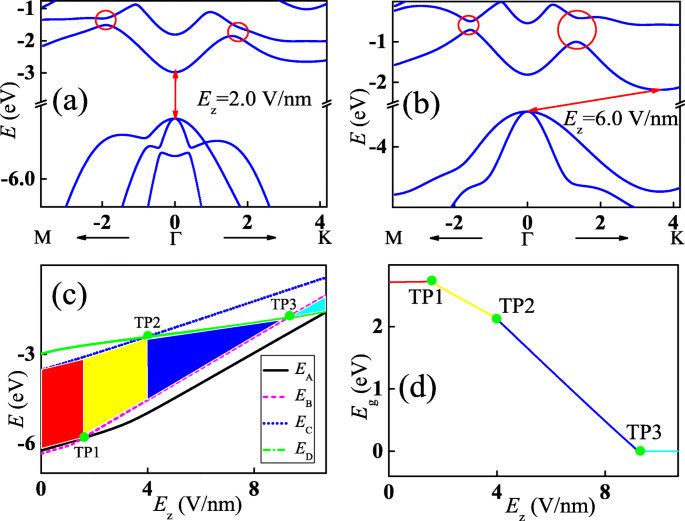
(Kleur online) Energiebanden van de loodrecht elektrisch veld-gemoduleerde monolaag InSe met verschillende sterktes E _z =2.0 V/nm(a ) en 6,0 V/nm (b ), respectievelijk. Rode cirkels in a en b betekent de geopende energiegaten rond de kruispunten getoond in Fig. 1c. c Energieën op de punten A (de zwarte ononderbroken lijn), B (de magenta stippellijn), C (de blauwe stippellijn) en D (de groene stippellijn) getoond in Fig. 1c als een functie van de elektrische veldsterkte . d Globale band gap als functie van de sterkte van het elektrische veld. De gele lijn betekent de directe band gap terwijl de rode en blauwe lijnen de indirecte band gaps aangeven

Om het veranderende proces van elektronische structuur van monolaag InSe in aanwezigheid van een loodrecht elektrisch veld duidelijker te begrijpen, energieën bij de golfvectoren die overeenkomen met punten A, B, C en D aan de bandranden getoond in Fig. 1c als functie van de sterkte van het elektrische veld zijn weergegeven in figuur 3c. Energieën met betrekking tot al deze punten bewegen naar boven als de elektrische veldsterkte toeneemt, wat de evolutie van de energiebanden in Fig. 3a en b bevestigt. Wanneer de elektrische veldsterkte E _z <1,6 V/nm, energie op punt A in de valentieband is hoger dan die van punt B, terwijl de onderkant van de geleidingsband zich op punt C bevindt. Daarom is de elektrisch veld-gemoduleerde monolaag InSe binnen dit sterktebereik een indirecte bandafstand halfgeleider, zoals weergegeven door het rode gebied. De energieën met betrekking tot de punten A en B zullen elkaar echter kruisen bij TP1, en dan zal de energie op punt B hoger zijn dan die van punt A naarmate de elektrische veldsterkte verder wordt vergroot. Tegelijkertijd blijft de onderkant van de geleidingsband ongewijzigd totdat de elektrische veldsterkte is verhoogd tot 4,0 V/nm. Als gevolg hiervan is het elektrisch veld-gemoduleerde monolaag InSe binnen dit sterktebereik een directe bandgap-halfgeleider, zoals weergegeven door het gele gebied. Net als de energie-crossover tussen de punten A en B in de valentieband, wordt het transitpunt ook waargenomen in de energieën op de punten C en D in de geleidingsbanden, zoals aangegeven door TP2. De energie op punt D is lager dan die van punt C, terwijl de bovenkant van de valentieband nog steeds op punt B blijft als alleen de elektrische veldsterkte kleiner is dan 9,23 V/nm. Dientengevolge wordt het elektrisch veld-gemoduleerde monolaag InSe weer omgezet in een indirecte bandgap-halfgeleider, zoals weergegeven door het blauwe gebied. Interessant is dat energieën op punt B in de hoogste valentieband en punt D in de laagste geleidingsband ook bij TP3 zullen kruisen, wat betekent dat de energiebandafstand gesloten is. Bovendien zal de energie op punt B hoger zijn dan die van punt D wanneer de elektrische veldsterkte groter is dan 9,23 V/nm. Daarom zullen de laagste geleidingsband en de hoogste valentieband elkaar overlappen, zodat het elektrisch veld-gemoduleerde monolaag InSe in dit geval een metaal wordt, zoals weergegeven door het cyaangebied. De globale bandafstand die overeenkomt met verschillende gekleurde gebieden in figuur 3c is uitgezet in figuur 3d. De bandafstand die overeenkomt met het rode gebied is bijna onafhankelijk van de gevarieerde elektrische veldsterkte, zoals weergegeven door de rode lijn. De bandafstand van het gele gebied neemt echter lineair af met toenemende elektrische veldsterkte. Vergelijkbaar bandgapgedrag wordt ook gevonden in het blauwe gebied, maar met een grotere helling. De band gap wordt teruggebracht tot nul zolang de elektrische veldsterkte groter is dan die op punt TP3, zoals weergegeven door de cyaan lijn. Het elektrisch veld-gemoduleerde bandgapgedrag geeft aan dat gelaagde III-VI halfgeleiders potentiële toepassingen hebben bij het ontwerpen van nieuwe optische detectoren en absorbers. Bovendien varieert de spectrale responsfrequentie van deze apparaten continu van het violette licht (ν ≈6.57×10¹⁴ Hz als E _z =1.6 V/nm) naar het infraroodlicht (ν <3.97×10¹⁴ Hz als E _z>5,18 V/nm).

Zoals bekend worden elektronische eigenschappen van materialen voornamelijk bepaald door energiebandranden. Volgens de orbitale decompositie voor de energieband in figuur 2 worden zowel de geleidings- als de valentiebandranden van monolaag InSe voornamelijk bijgedragen door p _z orbitaal van Se ion. Daarom alleen p _z orbitale ontledingen van Se ion in sublaag 2 voor energiebanden getoond in Fig. 3a en b worden weergegeven in Fig. 4a en b, respectievelijk. Door te vergelijken met Fig. 2h, p _z orbitale bijdrage aan de geleidingsbanden is enigszins veranderd. Daarom ondergaat de vorm van deze bandstructuren weinig affectie. Echter, de p _z De orbitale bijdrage aan de valentiebanden is sterk gewijzigd, wat resulteert in de vormverandering van deze bandstructuren. Bovendien, volgens de p _z orbitale ontleding voor de energieband van monolaag InSe met een loodrecht elektrisch veld, de relatieve positie van elke geleidingsband blijft ongewijzigd, hoewel openingen worden geopend bij bandkruisingen, zoals aangegeven door de rode cycli. Integendeel, de relatieve positie van elke valentieband is veranderd. De energieën van de lagere valentiebanden rond Γ punttoename en overtreft uiteindelijk die van de hoogste valentieband, wat leidt tot indirect-directe bandgapovergang.

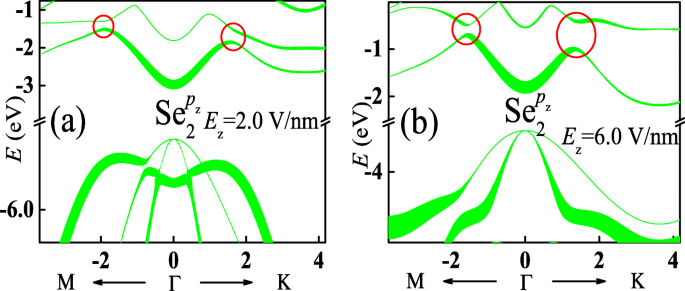
(Online kleuren) a en b toon p _z orbitale ontleding van het Se-ion in sublaag 2 voor de energiebanden van de monolaag InSe met een loodrecht elektrisch veld getoond in respectievelijk Fig. 3a en b. Dikkere lijnen vertegenwoordigen een belangrijkere bijdrage

Conclusies

Elektronische structuren van monolaag InSe onder de modulatie van een loodrecht elektrisch veld worden onderzocht. Indirect-direct-indirecte band gap-overgang wordt gevonden voor de monolaag InSe door de elektrische veldsterkte af te stemmen. Tegelijkertijd wordt de globale bandafstand van dit systeem monotoon tot nul verlaagd met toenemende elektrische veldsterkte, wat betekent dat de overgang van halfgeleider naar metaal wordt bereikt. De evolutie van de energieband van monolaag InSe in aanwezigheid van het loodrechte elektrische veld wordt verduidelijkt door de energieverandering van bandrand en orbitale decompositie voor energieband te analyseren. Deze resultaten kunnen nuttig zijn voor een beter begrip van de elektronische structuren van monolaag InSe en voor het ontwerpen van monolaag-InSe-gebaseerde foto-elektrische apparaten die reageren van violet tot ver-infrarood licht.

Beschikbaarheid van gegevens en materialen

De datasets die de conclusies van dit artikel ondersteunen, zijn in het artikel opgenomen.

Afkortingen

2D:: Tweedimensionaal
DFT:: Dichtheidsfunctionaaltheorie
TMD's:: Overgangsmetaal dichalcogeniden

Magnetisch veldversterkende fotokatalytische reactie in micro-optofluidic chipreactor Preparatie en farmacokinetisch onderzoek van lang-circulerende Daidzein-liposomen

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal