home Productietechnologie Fabricage-apparatuur
Industriële fabricage
Industrieel internet der dingen | Industriële materialen | Onderhoud en reparatie van apparatuur | Industriële programmering |
home  MfgRobots >> Industriële fabricage >  >> Industrial materials >> Nanomaterialen

Elektronische structuur en IV-kenmerken van InSe Nanoribbons

Abstract

We hebben de elektronische structuur en de stroom-spanning (I-V ) kenmerken van eendimensionale InSe-nanoribbons met behulp van de dichtheidsfunctionaaltheorie gecombineerd met de niet-evenwichtsfunctiemethode van Green. Er wordt rekening gehouden met nanolinten met kale of H-gepassiveerde randen van het type zigzag (Z), Klein (K) en fauteuil (A). Randtoestanden blijken een belangrijke rol te spelen bij het bepalen van hun elektronische eigenschappen. Randen Z en K zijn meestal metallisch in brede nanolinten en hun gehydrogeneerde tegenhangers. Overgang van halfgeleider naar metaal wordt waargenomen in gehydrogeneerde nanoribbons HZZH naarmate hun breedte toeneemt, vanwege de sterke breedte-afhankelijkheid van het energieverschil tussen de linker- en rechterrandtoestanden. Desalniettemin variëren elektronische structuren van andere nanolinten op zeer beperkte schaal met de breedte. De I-V kenmerken van kale nanoribbons ZZ en KK vertonen een sterke negatieve differentiële weerstand, als gevolg van ruimtelijke mismatch van golffuncties in energiebanden rond de Fermi-energie. Spinpolarisatie in deze nanoribbons wordt ook voorspeld. Daarentegen zijn kale nanolinten AA en hun gehydrogeneerde tegenhangers HAAH halfgeleiders. De band gaps van nanoribbons AA (HAAH) zijn smaller (breder) dan die van tweedimensionale InSe-monolaag en nemen toe (verlagen) met de nanoribbon-breedte.

Achtergrond

Atomair dunne tweedimensionale (2D) materialen hebben de afgelopen tien jaar veel belangstelling gewekt vanwege hun unieke elektronische eigenschappen en het veelbelovende toepassingspotentieel [1,2,3,4] dat voornamelijk voortkwam uit hun verminderde dimensionaliteit. Eendimensionale (1D) nanoribbons kunnen vervolgens worden gefabriceerd door de 2D-materialen [5] op maat te maken of atomen precies bottom-up te assembleren [6, 7]. In de nanoribbons worden de elektronische eigenschappen verder gemoduleerd door extra opsluiting en mogelijke edge-functionalisering [8, 9]. Hun energiekloof, een belangrijke parameter van halfgeleiders, kan bijvoorbeeld continu worden aangepast door hun breedte [10,11,12,13,14,15]. De bungelende bindingen van de randatomen kunnen worden gepassiveerd door H-atomen in de juiste omgeving, en de hydrogenering kan de randen stabiliseren door structurele reconstructie [16, 17].

Onlangs is een nieuw lid, de InSe monolayer, aan de 2D-materialen toegevoegd. Bulk InSe behoort tot de familie van gelaagde metalen chalcogenide halfgeleiders en is de laatste decennia intensief bestudeerd [18,19,20,21,22]. Elk van zijn viervoudige lagen heeft een hexagonaal rooster dat in feite bestaat uit vier covalent gebonden Se-In-In-Se atomaire vlakken. De viervoudige lagen worden op elkaar gestapeld door van der Waals-interacties op een tussenlaagafstand van ongeveer 0,8 nm. De stapelstijl definieert zijn polytypes zoals β, γ en ε, waaronder de β en γ die directe bandhiaten hebben. Desalniettemin werd de enkele viervoudige InSe-laag de afgelopen jaren alleen met succes vervaardigd door de mechanische exfoliatiemethode [23, 24]. Sindsdien hebben de waargenomen buitengewoon hoge elektronenmobiliteit en speciale fysieke eigenschappen van InSe-monolagen geleid tot uitgebreid onderzoek naar hun mogelijke toepassingen in opto-elektronische apparaten [24,25,26] en elektronische apparaten [27, 28]. Om nieuwe functionele eigenschappen te verkennen, kan theoretische studie ook een efficiënte benadering zijn. Numerieke simulaties van structurele, elektrische en magnetische eigenschappen van InSe-monolagen en hun modulatie door dotering, defecten en adsorptie zijn uitgevoerd [29,30,31,32,33,34,35,36,37,38]. De bandstructuren van mono- en paarlaags InSe zijn zorgvuldig bestudeerd door de dichtheidsfunctionaaltheorie [29]. De dominante intrinsieke defecten in InSe-monolaag zijn ontdekt [30], en de eigenschappen van natieve defecten en vervangende onzuiverheden in monolaag InSe zijn geschat door berekening van vormings- en ionisatie-energieën [31]. Bovendien is voorspeld dat substitutiedotering van As-atomen InSe-monolaag kan overbrengen van niet-magnetische halfgeleider naar magnetische halfgeleider/metaal of half-halfmetaal [32]. De thermische geleidbaarheid van InSe-monolagen kan sterk worden gemoduleerd door hun grootte [33]. Voor zover wij weten, zijn er tot nu toe echter weinig studies over elektronische eigenschappen van eendimensionale nanoribbons van InSe-monolaag.

In dit artikel voeren we eerste-principesimulaties uit op elektronische eigenschappen van 1D kale zigzag-, fauteuil- en Klein monolaag InSe-nanoribbons en hun waterstof-gepassiveerde tegenhangers. Onze studies wijzen op de overgang van halfgeleider naar metaal in waterstof-gepassiveerde InSe zigzag nanoribbons en de interessante verandering van de energiekloof in fauteuil nanoribbons. De stroom-spanningscurven tonen gediversifieerde elektrische eigenschappen voor nanolinten met verschillende randen.

Methoden

Er wordt rekening gehouden met de drie typische randpatronen van honingraatrooster, zigzag (Z), fauteuil (A) en Klein (K). Zoals geïllustreerd in Fig. 1 kan een nanoribbon worden geïdentificeerd door zijn breedtegetal n en de combinatie van de typen van de twee randen. Er zijn vijf klassen van kale nanolinten:n -ZZ, n -AA, n -KK, n -ZK, en n -KZ. Merk op dat n -ZK is anders dan n -KZ omdat we aannemen dat de linker (rechter) Z-rand eindigt op In (Se)-atomen. Als elk randatoom wordt gepassiveerd door één waterstofatoom, duiden we de gepassiveerde nanoribbons aan als n -HZZH, n -HAAH, n -HKKH, n -HZKH, en n -HKZH, respectievelijk. Een Se-In-In-Se viervoudige laag met roosterconstante 4,05 met Se-In laagafstand 0,055 en In-In laagafstand 0,186 Å wordt gebruikt om nanolinten te maken vóór optimalisatie van de geometrie [21].

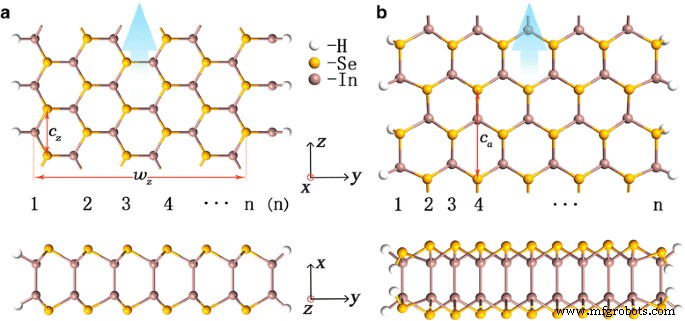
Boven- en zijaanzichten van 6-HZKH (a ) en 11-HAAH (b ) InSe nanolinten. Breedte van nanolint n , breedte w z , en roosterconstanten c z of c een zijn gemarkeerd

Alle berekeningen worden uitgevoerd met behulp van de Atomistix ToolKit (ATK) op basis van DFT met de pseudopotentiaaltechniek. De uitwisselingscorrelatie functioneel in de lokale spindichtheidsbenadering met de Perdew-Zunger-parameterisatie (LSDA-PZ) wordt aangenomen. De golffuncties worden uitgebreid op een basisset van dubbele orbitalen plus één polarisatieorbitaal (DZP). Een energie-uitschakeling van 3000 eV, a k -ruimtemaasraster van 1 × 1 × 100 en een elektronische temperatuur van 300 K worden gebruikt in de real-axis-integratie voor de niet-evenwichtsfuncties van Green. Een 15-Å dikke vacuümlaag in de supercellen wordt gebruikt om de nanoribbons te scheiden van hun naburige afbeeldingen in beide x en y richtingen en om de onderdrukking van de koppeling daartussen te verzekeren. Bandstructuren worden berekend na volledige relaxatie van de geometrie met een krachttolerantie van 0,02 eV/Å −1 .

Om de elektronische transporteigenschap van de nanoribbons te simuleren, verbinden we ze elk in een circuit met een links (rechts) chemisch potentieel μ L (μ R ) [40, 41]. Het nanolint kan dan worden verdeeld in drie gebieden, de linker (rechter) elektrode L (R) en het centrale gebied C. De spinafhankelijke stroom kan worden geschat met de Landauer-Büttiker-formule [42].

$$ {I}_{\sigma}\left({V}_b\right)=\frac{e}{h}{\int}_{-\infty}^{+\infty }{T}_{ \sigma}\left(E,{V}_b\right)\left[{f}_L\left(E-{\mu}_L\right)-{f}_R\left(E-{\mu}_R \right)\right] dE $$

met draai σ =  ↑ , ↓ en spanningsbias V b = (μ R − μ L )/e . Hier, \( {T}_{\sigma}\left(E,{V}_b\right)=Tr\left[{\Gamma}_L{G}_{\sigma }{\Gamma}_R{G} _{\sigma}^{\dagger}\right] \) is het transmissiespectrum met G σ de functie van de achterlijke Groen in regio C en Γ L (Γ R ) de koppelingsmatrix tussen C en L (R). f L (f R ) is de Fermi-verdelingsfunctie van elektronen in L (R).

Resultaten en discussie

In Fig. 1 schetsen we de boven- en zijaanzichten van (a) 6-HZKH en (b) 11-HAAH nanoribbons met roosterconstanten c z = 4.05 Å en c een = 7.01 Å, respectievelijk. Rand K is in de richting evenwijdig aan die van rand Z. De uitstrekkende richting z van het nanolint is gemarkeerd met blauwe pijlen. Anders dan bij grafeen nanoribbon [39], wordt er geen randreconstructie waargenomen voor de drie randstijlen in zowel kale als H-gepassiveerde InSe nanoribbons, en onze simulatie geeft aan dat ze allemaal energetisch stabiel zijn.

Bare n -ZZ nanoribbons zijn magnetisch metaal, behalve de 2-ZZ die een gereconstrueerde geometrie heeft en halfgeleider lijkt. Ze hebben vergelijkbare bandstructuren zoals geïllustreerd in figuur 2a. De p orbitalen van rand Se-atomen domineren de bijdrage aan de toestanden nabij de Fermi-energie, vergelijkbaar met het geval van InSe-monolaag [32], maar hier worden meer bijdragen van de In-atomen waargenomen. De twee gedeeltelijk bezette banden zijn respectievelijk van de linker- en rechterrandtoestanden, zoals blijkt uit de Г-punt Bloch-toestanden voor 4-ZZ nanoribbon. Een daarvan is spin-splitsing en een netto magnetisch moment, bijvoorbeeld 0,706 μB voor 4-ZZ nanoribbon, verschijnt in elke primitieve cel aan de linkerrand.

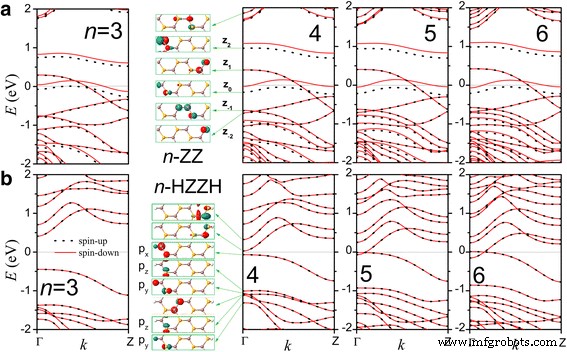
De bandstructuren van a 3-, 4-, 5- en 6-ZZ nanolinten en b 3-, 4-, 5- en 6-HZZH nanolinten. Г-punt Bloch-toestanden nabij de Fermi-energie worden getoond voor n =4. De banen van de toestanden onder de Fermi-energie zijn aangegeven voor 4-HZZH nanoribbon

Wanneer de randatomen worden gepassiveerd door H-atomen, n -HZZH nanoribbons worden niet-magnetische halfgeleider voor n = 3, 4 en metaal voor n> 4 zoals weergegeven in Fig. 2b. Merk op dat de structuur instabiel wordt voor n =  2. In 4-HZZH nanoribbon zijn de Bloch-toestanden bij Г in geleidingsbanden (valentie) nabij de Fermi-energie beperkt tot de rechter (linker) rand. Ze hebben componenten die vergelijkbaar zijn met die in 2D InSe-monolaag, behalve de H-atomaire orbitale delen. De hoogste vijf banden van de linkerrandtoestanden zijn samengesteld uit één p x , twee p j , en twee p z orbitalen van Se-randatomen. De energiebanden van de rechter (linker) randtoestanden zijn vergelijkbaar met de geleidingsbanden (valentie) in de Γ-K-richting van de 2D InSe-monolaag [32]. Hun scheiding in energie hangt sterk af van n hoewel hun verspreiding ongevoelig is voor n . We definiëren E d als het energieverschil tussen het minimum van de toestanden van de rechterrand en het maximum van de toestanden van de linkerrand.

In Fig. 3 plotten we E d versus n en w z en vond ongeveer een omgekeerde afhankelijkheid E d ≈ E 0 + een /(w z − w 0 ) met E 0 =  − 0.45eV, w 0 = 4Å, en a = 4eVÅ. Dit gedrag is vergelijkbaar met de breedte-afhankelijkheid van de energiekloof in zigzag-grafeen en BN-nanoribbons [12,13,14,15, 43,44,45,46,47] die de oorsprong hebben van elektron-elektron-interactie. Smalle HZZH InSe-nanoribbons zijn halfgeleiders en naarmate de breedte groter wordt, vindt een overgang van halfgeleider naar metaal plaats.

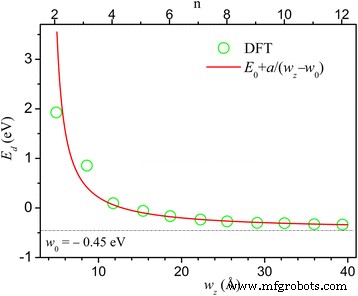
De minimale energieverschillen E d tussen de rechter- en linkerrandtoestanden nabij de Fermi-energie in n -HZZH nanoribbons worden getoond versus n en w z . De pasvormcurve is rood

De bandstructuren van n -KK en n -HKKH nanoribbons zijn niet gevoelig voor het breedtegetal n zoals geïllustreerd in respectievelijk Fig. 4a, b voor n =4. In vergelijking met de zigzagrand heeft de blote Klein-rand meer bungelende banden, wat resulteert in een significante verandering van de bandstructuur. Orbitalen van rand Se-atomen hebben meestal een lagere energie dan die van rand In-atomen, vergelijkbaar met ZZ-nanoribbon. In HKKH nanoribbons, de onderdrukking van de p orbitaal van rand In atomen en de p orbitaal van rand Se-atoom door de passivering van H-atomen is duidelijk. Toch is één H-atoom niet genoeg om alle bungelende bindingen van de randatomen te passiveren. Zowel KK- als HKKH-nanolinten zijn van metaal.

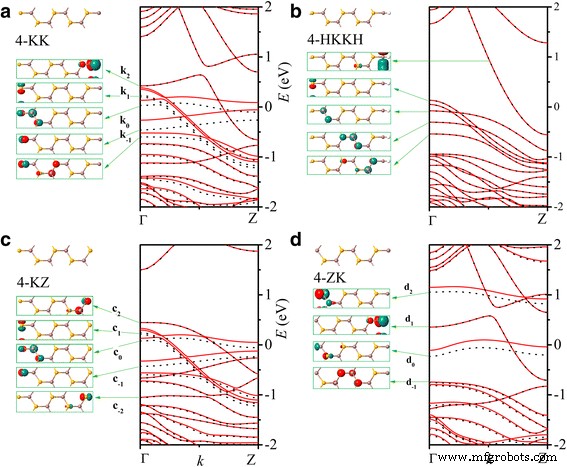
De bandstructuren en Γ-punts Bloch-toestanden van 4-KK (a ), 4-HKKH (b ), 4-KZ (c ), en 4-ZK (d ) nanolinten

In nanoribbons met een vermenging van zigzag- en Klein-randen, zien we een combinatie van energiebanden van de twee soorten randen in de buurt van de Fermi-energie. Zoals weergegeven in figuur 4c voor het 4-KZ nanolint, de dispersie en Γ-punt Bloch-toestanden van banden c1 , c0 , en c−1 zijn dezelfde als die van band k1 , k0 , en k−1 in 4-KK nanoribbon zoals uitgezet in Fig. 4a, terwijl banden c2 en c−2 zijn hetzelfde als band z1 en z−2 van 4-ZZ nanoribbons in figuur 2a. Evenzo is de bandstructuur van het 4-ZK-nanoribbon, zoals geïllustreerd in figuur 4d, samengesteld uit band d1 van rechts Klein rand en banden d2 , d0 , en d−1 vanaf de linker zigzagrand. Sinds n -ZK en n-KZ nanoribbons behouden een deel van de energiebanden van n -KK nanoribbons in de buurt van de Fermi-energie, ze zijn zowel metaal als de n -KK nanolinten. Om dezelfde reden zijn de H-gepassiveerde nanolinten die de randen Z en K mengen ook van metaal.

Zowel de AA- als de HAAH-nanoribbons zijn niet-magnetische halfgeleiders zoals weergegeven in figuur 5a, b, waar de bandstructuren zijn uitgezet voor n = 4, 5. De passivering van H-atomen kan de structurele stabiliteit energetisch verbeteren en de energiekloof vergroten. Interessant is dat de energiekloof een zigzag-afhankelijkheid heeft van de nanoribbonbreedte, en een oneven-even familieachtig gedrag vertoont zoals in grafeen en BN nanoribbons [10,11,12,13,14,15, 43,44,45,46, 47]. Zoals geïllustreerd in Fig. 5c, n -AA-nanolinten hebben een opening (olijfvierkant) die smaller is dan die van 2D InSe-monolaag (rood streepje). De opening neemt monotoon toe (verkleint) met de breedte voor oneven (even) n en convergeert naar een waarde van 1,15 eV bij de grote breedtelimiet wanneer de twee randen van elkaar worden ontkoppeld en hun energie stabiel is [13]. De Bloch-toestanden van valentiebandmaximum (VBM) op Г-punt en geleidingsbandminimum (CBM) op Z-punt worden ook getoond in figuur 5c. Het pariteitsgedrag wordt opnieuw waargenomen met de symmetrische (n = 5) of diagonaal (n = 4, 6) verdeling van de toestanden rond rand Se-atomen bij VBM en rond rand In-atomen bij CBM.

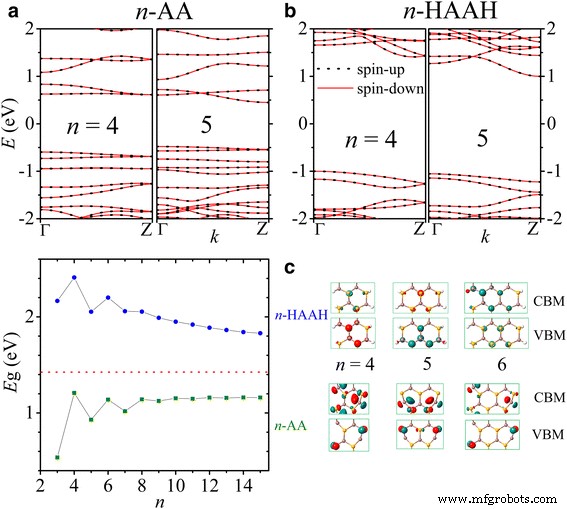
De bandstructuren van 4- en 5-AA nanoribbons worden getoond in a en die van 4- en 5-HAAH in b . De energiekloven E g van n -AA (groen) en n -HAAH (blauwe) nanoribbons zijn uitgezet tegen n in c met de opening van de InSe-monolaag (rood) gemarkeerd. De Bloch stelt bij CBM en VBM voor n = 4, 5 en 6 worden weergegeven in de rechterpanelen van c

Aan de andere kant, de hiaten van n -HAAH nanoribbons (blauwe cirkel) zijn breder dan hun 2D-tegenhanger en nemen af ​​met de breedte voor zowel oneven als even n . In gepassiveerde nanoribbons hebben de Bloch-staten bij VBM en CBM veel minder randcomponent. De corresponderende energiekloven zijn ongeveer 1 eV groter dan die van de naakte nanolinten, en het verschil wordt kleiner naarmate de breedte toeneemt [13].

In Fig. 6a tonen we de stroom-spanning (I -V ) kenmerk van bovenstaande metalen InSe nanoribbons 4-ZZ (vierkant), 4-KK (cirkel) en 4-HKKH (driehoek). Spin-up (spin-down) curves worden gemarkeerd door gevulde (lege) symbolen. De Landauer-Büttiker-formule is gebruikt om de spinafhankelijke stroom I . te berekenen σ wanneer een spanningsbias V b wordt aangebracht tussen elektroden L en R, met μ R = eV b /2 en μ L =  − eV b /2 verondersteld. Negatieve differentiële weerstand (NDR) en spinpolarisatie worden waargenomen in kale nanolinten van 4-ZZ en 4-KK onder een afwijking in het gebied tussen 0,5 en 1,2 V. De piek-tot-dalverhouding van NDR is groter dan 10 voor de 4- ZZ nanoribbon vanwege de transversale mismatch van golffuncties tussen energiebanden nabij de Fermi-energie zoals geïllustreerd in figuur 2a en uitgelegd in het volgende. Band z1 is het dominante transportkanaal onder V b <-1,2 V zoals aangegeven door de spin-up en spin-down transmissiespectra in respectievelijk Fig. 6b, c. De golffuncties van band z1 zijn orthogonaal op of zijn in de ruimte gescheiden van die van nabije banden z2 , z−1 , en z−2 . Dit leidt tot de mismatch tussen de toestanden z1 in één elektrode en die met dezelfde energie in de andere elektrode onder V b . De elektronen van band z1 in de ene elektrode hebben dan moeite om met energiebesparing naar de andere elektrode te transporteren. Het resultaat is dat de I-V curve van nanoribbon 4-ZZ toont een enkelbandskarakteristiek met sterke NDR. Verder is de spin-splitsing van band z0 leidt tot de spinpolarisatie in het lineaire regime. In het gepassiveerde 4-HKKH-nanoribbon verzadigt de stroom echter in het bovengenoemde NDR-biasgebied.

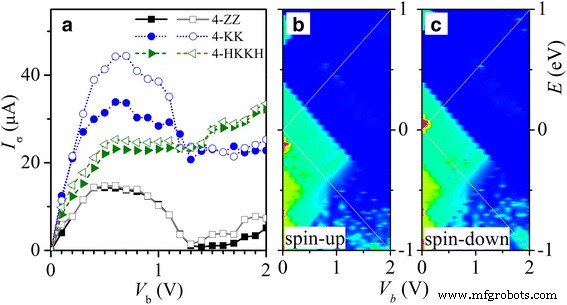
een De spin-up (gevuld) en spin-down (leeg) I -V kenmerken van 4-ZZ (vierkant), 4-KK (cirkel) en 4-HKKH (driehoek) InSe nanoribbons worden gepresenteerd. De bijbehorende transmissiespectra van spin-up (b ) en spin-down (c ) worden getoond voor het 4-ZZ nanoribbon. Het transportvenster tussen μ L en μ R wordt gemarkeerd door de witte lijnen

Conclusies

We hebben systematisch de elektronische eigenschappen onderzocht van InSe-nanoribbons met Z-, A- of K-randen. De randen spelen een sleutelrol bij het bepalen van de eigenschappen, aangezien elektronentoestanden in de buurt van de Fermi-energie een groot gewicht hebben aan randatomaire orbitalen. Kale Z- en K-randen zijn geleidend en magnetisch. Sterke edge-edge interactie kan leiden tot de overgang van n -HZZH nanoribbons van halfgeleider naar metaal als n neemt toe. Als gevolg hiervan zijn kale en H-gepassiveerde nanolinten met Z- en K-randen van metaal, behalve zeer smalle. n -AA en n -HAAH zijn niet-magnetische halfgeleiders met energiekloven die respectievelijk smaller en breder zijn dan die van InSe-monolaag. Hun gaten naderen elkaar op een zigzaggende manier als n neemt toe en vertoont een even oneven gedrag. De stroom-spanningscurven van ZZ- en KK-nanoribbons worden gekenmerkt door sterke enkelbands NDR en spinpolarisatie.

Afkortingen

1D:

Eendimensionaal

2D:

Tweedimensionaal

A:

Fauteuil

CBM:

Minimaal geleidingsband

K:

Klein

VBM:

Maximale valentieband

Z:

Zigzag


Nanomaterialen

  • Metaal
  • Hars
  • vezel
  • Samengesteld materiaal
  • Nanomaterialen
  • Polymeer materialen
  • Biologie
  • kleurstof
  • Kruiden
    1. Kenmerken en gebruik van W-Ag-legering
    2. Kenmerken en toepassingen van titanium
    3. Tantaalcondensatorkenmerken en toepassingen
    4. Hafniumoxide en zijn structuur en toepassingen
    5. Valentie en kristalstructuur
    6. C Structuur en functie
    7. Silicon Photomultiplier (SiPM) structuur, kenmerken en toepassingen
    8. Typen en kenmerken van glasvezeldoek
    9. Kenmerken en toepassingen van glasvezel plakband
    10. Aluminium eigenschappen en legeringskenmerken
    11. Verschil tussen structuur en unie