Invloed van water op de structuur en diëlektrische eigenschappen van microkristallijne en nano-cellulose

Resultaten en discussie

Thermogravimetrische onderzoeken

Onderzoeken van de hoeveelheid water in MCC werden uitgevoerd met behulp van derivatograph Q-1500D. In het onderzochte monster was de temperatuur (T ), massale verandering (m ), en snelheid van de massaverandering (dm/dT ) werden gelijktijdig gemeten en er werden differentiële en thermische analyses (DTA) uitgevoerd.

Temperatuurafhankelijkheden van de relatieve massaverandering Δm /m ₀ = (mam ₀ )/m ₀ , m ₀ ––initiële monstermassa (zie Fig. 1) en afgeleide van de massaverandering dm/dT (zie Fig. 2) werden verkregen.

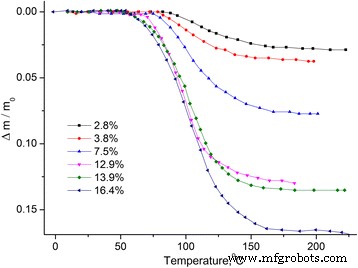
Temperatuurafhankelijkheid van de relatieve massaverandering van MCC. Temperatuurafhankelijkheid van de relatieve massaverandering Δm /m ₀ van MCC-monsters met verschillende waterinhoud

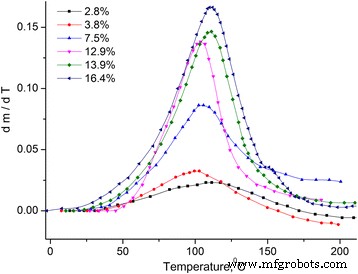
Temperatuurafhankelijkheid van de afgeleide van massaverandering van MCC. Temperatuurafhankelijkheid van de afgeleide van massaverandering dm /dT van MCC-monsters met verschillende waterinhoud

Men kan bedenken dat het massaverlies door het monster wordt veroorzaakt door de verdamping van water, dat zich in verschillende toestanden in het monster bevindt [12, 13]. Daarom is de dm /dT werd verdeeld over pieken met behulp van de Gauss-verdeling (zie Fig. 3).

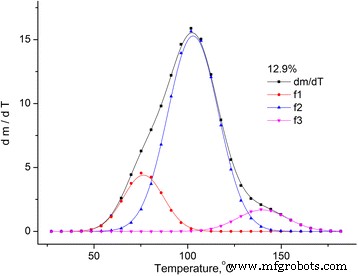
Benadering van de dm /dT afhankelijkheid voor MCC-monster met een vochtigheid van 12,9%. Benadering van de dm /dT afhankelijkheid voor MCC-monster met een vochtigheid van 12,9% met behulp van Gauss-verdeling met drie pieken

De afhankelijkheid van dm /dT voor elk van de onderzochte monsters kan worden beschreven door de superpositie van drie pieken. De eerste piek (f ₁ ) is verbonden met de verdamping van water van fysisch-mechanische binding met MCC, die zich in de microporiën van het monster bevindt, de tweede (f ₂ ) wordt veroorzaakt door het water van polymoleculaire en monomoleculaire hydraatlagen en de derde piek wordt veroorzaakt door de thermische oxidatieve afbraak van het monster.

In tabel 1 percentage S ₁ in het kwadraat van de algemene piek dm /dT en massapercentage w _ik = CS _ik /100% in algemene massa van verschillende soorten water en vernietiging voor de MCC-monsters met verschillende waterinhoud wordt getoond.

Het blijkt dat de hoeveelheid fysiek mechanisch gebonden water S ₁ neemt toe met de groei van het algemene watergehalte en de hoeveelheid water in hydraatschillen S ₂ neemt ook toe en bereikt zijn verzadiging bij een concentratie van het algemene water van 12,9%.

Laten we in meer detail kijken naar de tweede piek (f ₂ ), die wordt veroorzaakt door uitdroging van cellulosekristallen.

De methode voor het berekenen van kinetische parameters van het dehydratatieproces, zoals de activeringsenergie E en pre-exponentiële factor (k ₀ ) worden beschreven in [12]. Kinetische vergelijking van het desorptieproces kan worden weergegeven als:

Een mate van bedekking van cellulosekristallieten door de watermoleculen (Q ) verandert van 1 (voor het oorspronkelijke materiaal) in 0 (het hele water is uitgedroogd). Een volgorde van reactie (n ) is een geheel getal van 1 tot 3; er wordt vanuit gegaan dat het bekend is uit het experiment. De constante van de reactiesnelheid (k ) kan worden geschreven als:

waar R is een universele gasconstante. De waarde van E wordt in deze benadering als een constante genomen, wat een equivalentie betekent van alle hydratatiecentra van het MCC-kristallenoppervlak. De pre-exponentiële factor kan worden geschreven als k ₀ = ZP , waarbij Z is het theoretische aantal discontinuïteiten van waterstofbruggen tussen watermoleculen en cellulose (MCC) in een hydraatlaag per tijdseenheid, en P is een waarschijnlijkheidsfactor die rekening houdt met alle effecten die worden veroorzaakt door een afwijking van de idealiteit. De kans op het verbreken van de waterstofbinding tussen het watermolecuul en de cellulose is veel groter bij een hogere concentratie van watermoleculen in de gehydrateerde schil, dus het watermolecuul vormt na de bindingsbreuk geen nieuwe binding met de aangrenzende vrije knoop, maar vertaalt vanuit de hydraatlaag. Daarom is de pre-exponentiële factor van de reactiesnelheid klein bij de lage waterconcentraties en neemt toe met de groei van de waterconcentratie in de gehydrateerde schaal. Wanneer verzadiging van de gehydrateerde schaal is bereikt (alle knooppunten zijn bezet), dan k ₀ is niet afhankelijk van de concentratie van het vocht. Dit wordt waargenomen voor het MCC-watersysteem bij een concentratie van meer dan 12,9%.

Na vervanging van Vgl. 1 in verg. 2 en logaritme, krijgen we:

Onder beginvoorwaarden Q _{t= 0} = 1, Q _t=∞ = 0 en constante verwarmingssnelheid (β ), d.w.z. bij lineaire afhankelijkheid van de temperatuur op tijd

de volgende relaties zijn vervuld

waar S ₀ en S _T zijn de gebieden op het perceel f ₂ onder de hele piek en het deel van de piek van T naar

Als alle veronderstellingen die in deze methode zijn geplaatst correct zijn en de volgorde van reactie n juist is gekozen, dan is de afhankelijkheid \( \ln \left[\frac{-dQ/dt}{Q^n}\right] \) van de inverse temperatuur (Vgl. 3) lineair in het hele temperatuurbereik. Experimentele waarden van f . hebben ₃ en β , met behulp van uitdrukkingen Vgl. 5 en 6, kan men Q . verkrijgen en dQ /dt , en parameters van niet-isotherme kinetiek k ₀ en E worden berekend uit Vgl. 3.

Een voordeel van deze methode is het gebruik van de hele reeks experimentele gegevens, inclusief het hoge temperatuurgedeelte van het thermogram, wat vooral belangrijk is bij het bepalen van de orde n , bepaling van het reactiemechanisme en eerlijkheid van het model.

De afhankelijkheden van \( \ln \left[\frac{-dQ/dt}{Q^n}\right] \) van een omgekeerde temperatuur voor de onderzochte standaarden (Fig. 4) werden gebouwd. Deze afhankelijkheden worden benaderd door rechte lijnen met behulp van de kleinste-kwadratenmethode. Het is gebleken dat de hoogste coëfficiënt van Pearson wordt waargenomen bij n = 2.

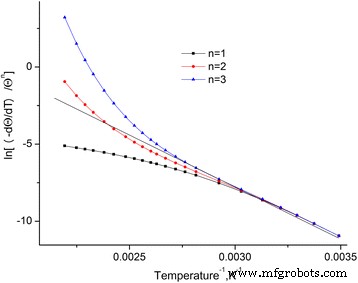
Afhankelijkheid van \( \ln \left[\frac{-dQ/dt}{Q^n}\right] \) van de omgekeerde temperatuur voor verschillende reactieordes. Afhankelijkheid van \( \ln \left[\frac{-dQ/dt}{Q^n}\right] \) van de omgekeerde temperatuur voor verschillende reactieorden

Berekende activeringsenergie (E ) en pre-exponentiële factor (k ₀ ) van de onderzochte MCC-monsters worden weergegeven in Tabel 2 (zie Fig. 5). Ervan uitgaande dat de activeringsenergie verband houdt met de opname van de waterstofbruggen, die 25 k omvatten J/mol [10], het is mogelijk om hun aantal N . te berekenen ₁ (zie Tabel 2).

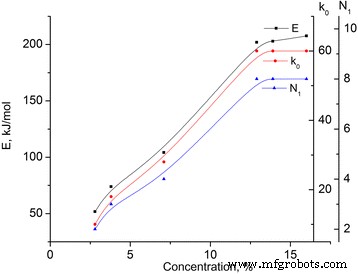
Afhankelijkheden van activeringsenergie (E ), pre-exponentiële factor (k ₀ ), en aantal waterstofbruggen N ₁ voor de monsters van MCC. Afhankelijkheden van activeringsenergie (E ), pre-exponentiële factor (k ₀ ), en aantal waterstofbruggen N ₁ voor de monsters van MCC met verschillende waterinhoud

Het is te zien dat met de groei van de concentratie van fysiek en chemisch gebonden water, de toename van activeringsenergie (E ) wordt waargenomen en bij een concentratie van 12,9% bereikt het zijn verzadiging. De waarde van activeringsenergie voor de verzadigde toestand komt overeen met acht waterstofbruggen.

Daarom kunnen we aannemen dat bij een waterconcentratie van 12,9% de continue hydraatschil van MCC-kristallen in het monster wordt gevormd.

Röntgendiffractieanalyse

De afhankelijkheden van afgebogen röntgenstralingsintensiteit voor microkristallijne cellulose met verschillende waterconcentraties op diffractiehoek I (2θ ) binnen het hoekenbereik [5 ÷ 45]° (zie Fig. 6) met de stap van hoekverandering van 0,1° werden verkregen.

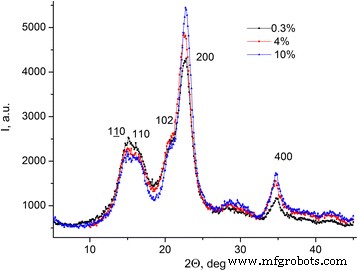
Afhankelijkheden van de intensiteit van afgebogen röntgenstraling voor MCC. Afhankelijkheden van de intensiteit van afgebogen röntgenstraling voor MCC met verschillende waterconcentraties op de diffractiehoek I (2θ )

Maxima, die overeenkomen met verschillende kristallografische vlakten, worden waargenomen op het MCC-röntgendiffractogram (zie Fig. 6).

De mate van kristalliniteit (C _k ) van MCC werd berekend door de integrale intensiteit van röntgenverstrooiing als een verhouding van structurele reflexen tot totale intensiteit van het diffractiepatroon exclusief achtergrond in het bereik 2θ [5 ÷ 45]° (zie Afb. 6). Gegevens van C _k voor MCC-monsters worden weergegeven in Tabel 3 [14].

Dwarsafmetingen van cellulosekristallieten in de normale richting van het systeem werden berekend met de Debye-Sherrer-formule [15].

waar k = 0,94---dimensieloze vormfactor, λ---golflengte van CuKα-straling (1,54178 Å); h ---halve breedte van (hlk) reflex, θ _hlk ---hoek van diffractie van het (hlk) vlaktesysteem. Urotropine werd gebruikt als een etalon voor meer vertrouwen. Instrumentele fout werd geschat met behulp van het etalon en correcties voor de halve reflexbreedte werden berekend.

Gegevens van afmetingen B _hlk voor MCC-monsters met verschillende waterinhoud en kristalliniteit worden weergegeven in Tabel 3.

Uit de verkregen resultaten (Tabel 3 en Fig. 7) volgt dat de transversale dimensie van kristallieten en kristalliniteit toenemen met de waterconcentratie. Groei van afmetingen vindt plaats in verschillende richtingen op ongeveer 0,4 nm. De gemiddelde diameter van het cellulosemolecuul is in de orde van d =0,8 nm. Daarom kan met de groei van de waterconcentratie een ordening van cellulosemoleculen in de grenslaag optreden, en als gevolg daarvan kan een toename van de transversale dimensie van cellulosekristallieten en kristalliniteit plaatsvinden.

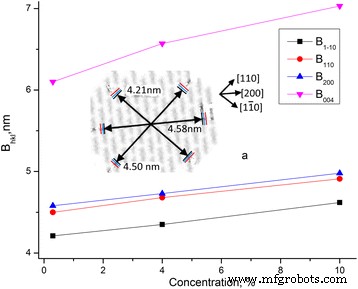
Afhankelijkheden van de afmetingen van kristalliet van MCC B _hlk op watergehalte. Afhankelijkheden van de afmetingen van kristalliet van MCC B _hlk op watergehalte, a--transversale afmetingen van MCC kristalliet (zwart ) en groei van zijn dimensie met de vochtigheidstoename (blauw ---MCC + 4% en rood ---MCC + 10%)

Diëlektrische eigenschappen van MCC

Temperatuurafhankelijkheden van de reële en imaginaire delen van de complexe diëlektrische permittiviteit binnen het temperatuurbereik [−180 ÷ 120] °C op de frequenties f = 5, 10, 20 en 50 kHz voor de monsters MCC + 0.3% H₂ O (zie Fig. 8 en 9) werden onderzocht.

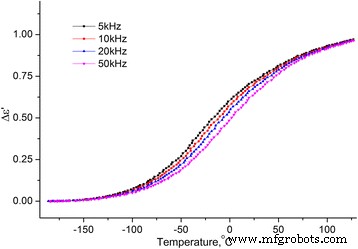
Temperatuurafhankelijkheid van de verandering van de toename van het reële deel van de complexe diëlektrische permittiviteit. Temperatuurafhankelijkheid van de verandering van de toename van het reële deel (Δε ′ = ε ′(T ) − ε _∞ , \( {\varepsilon}_{\infty }={\left.{\varepsilon}^{\prime}\right|}_{T=-180{}^o\mathrm{C}} \)) van de complexe diëlektrische permittiviteit MCC + 0,3% H₂ O op de frequenties 5, 10, 20 en 50 kHz

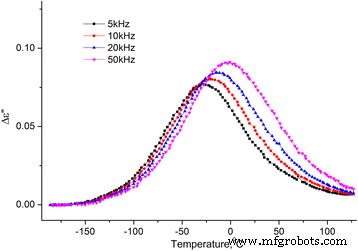
Temperatuurafhankelijkheid van het denkbeeldige deel van de diëlektrische permittiviteit van MCC + 0,3% H₂ O. Temperatuurafhankelijkheid van het denkbeeldige deel van de diëlektrische permittiviteit van MCC + 0,3% H₂ O op frequenties 5, 10, 20 en 50 kHz

Van de twee processen die zijn waargenomen op de temperatuurafhankelijkheden van ∆ε ′(T ) en ε ′′(T ), de lage temperatuur is een relaxatie aangezien het maximum op ∆ε ′(T ) en de verbuiging op ε ′′(T ) wordt verschoven met toenemende frequentie. Gewoonlijk wordt dit proces het β-proces genoemd, het moleculaire mechanisme ervan is niet definitief vastgesteld. We nemen aan dat het verband houdt met de heroriëntatie van methylolgroepen op het oppervlak van de kristallieten van de MCC, en deze heroriëntatie vindt plaats met een verandering in de conformatie van de methylolgroepen tg naar tt , het verbreken van de intramoleculaire H-binding en de vorming van de H-binding met het geadsorbeerde watermolecuul [16].

Het proces bij hoge temperatuur van de afhankelijkheden ∆ε ′(T ) en ε ′′(T ) verschuift niet met de frequentievariatie, de intensiteit neemt toe met de concentratie van het water in de MCC (zie figuren 10 en 11). We nemen aan dat de reden hiervoor de desorptie van het water is bij toenemende temperatuur met de daaropvolgende condensatie in de poriën, wat leidt tot een duidelijke stijging van de temperatuur ε ′ en ε ′ van het monster. Met de verdere temperatuurstijging treedt de verdamping van water op, en ∆ε ′(T ) en ε ′′(T ) afnemen.

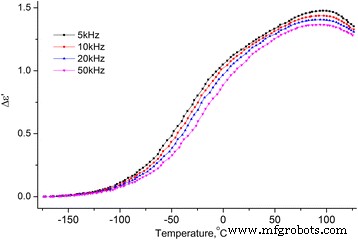
Temperatuurafhankelijkheid van de toename van het reële deel van de diëlektrische permittiviteit MCC + 2,8% H₂ O. Temperatuurafhankelijkheid van de toename van het reële deel (Δε ′ = ε ′(T ) − ε _∞ , waarbij \( {\varepsilon}_{\infty }={\left.{\varepsilon}^{\prime}\right|}_{T=-180{}^oC} \)) van de diëlektrische permittiviteit MCC + 2,8% H₂ O op frequenties 5, 10, 20 en 50 kHz

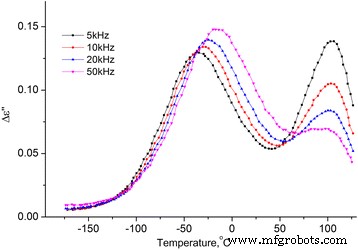
Temperatuurafhankelijkheid van het denkbeeldige deel van de diëlektrische permittiviteit van MCC + 2,8% H₂ O. Temperatuurafhankelijkheid van het denkbeeldige deel van de diëlektrische permittiviteit van MCC + 2,8% H₂ O op frequenties 5, 10, 20 en 50 kHz

In Fig. 12, afhankelijkheden van de toename van het reële deel (Δε ′ = ε ′(T ) − ε _∞ , waarbij \( {\varepsilon}_{\infty }={\left.{\varepsilon}^{\prime}\right|}_{T=-180{}^oC} \)) van de diëlektrische permittiviteit op temperatuur op frequentie 10 kHz worden gepresenteerd voor onderzochte monsters van MCC met verschillende watergehalten.

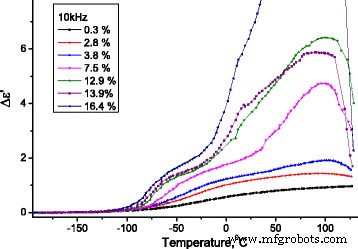
Temperatuurafhankelijkheid van de verandering van de toename van het reële deel van de diëlektrische permittiviteit van MCC. Temperatuurafhankelijkheid van de verandering van de toename van het reële deel (Δε ′ = ε ′(T ) − ε _∞ , waarbij \( {\varepsilon}_{\infty }={\left.{\varepsilon}^{\prime}\right|}_{T=-180{}^oC} \)) van de diëlektrische permittiviteit van MCC-monsters met verschillende waterinhoud

Het werd aangetoond in [16] dat relaxatieproces bij lage temperatuur, dat verband houdt met de overgang van de methylolgroep van tg naar tt conformatie, kan worden beschreven door het model met één relaxatietijd [17]

en voor de toename van de diëlektrische permittiviteit is de volgende formule geldig:

waar ε ′(T)–– is de diëlektrische permittiviteit van het monster bij temperatuur T , N is de concentratie van relaxatieoscillatoren, μ ² is het gemiddelde kwadraat van het verschil van dipoolmomenten van relaxatieoscillatoren in twee evenwichtsstanden, en V is het verschil in energieën van relaxatieoscillatoren in deze evenwichtsposities.

Tijdens de benadering van de afhankelijkheid van de toename van het reële deel van de complexe diëlektrische permittiviteit voor MCC-monsters met verschillende vochtigheid door de afhankelijkheid (Vgl. 9), waarden van N en V werden verkregen (zie tabel 4) met betrekking tot het verschil van dipoolmomenten van relaxatieoscillatoren in twee evenwichtsposities, die werd berekend met betrekking tot de ruimtestructuur van de methylolgroep μ = 5.57D = 18.381 ⋅ 10 ^− 30 C ⋅ m .

Uit tabel 4 blijkt dat bij de groei van het watergehalte het energieverschil V verandert niet, maar de concentratie van methylolgroepen, die bijdraagt ​​aan diëlektrische relaxatie, neemt toe.

In Fig. 13, afhankelijkheden van het denkbeeldige deel van de diëlektrische permittiviteit van de temperatuur op de frequentie f = 10 kHz voor bestudeerde monsters van MCC met verschillende waterinhoud worden weergegeven.

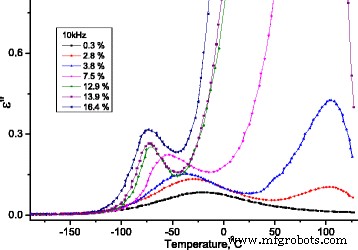
Temperatuurafhankelijkheid van het denkbeeldige deel van de diëlektrische permittiviteit voor MCC-monsters met verschillende waterinhoud. Temperatuurafhankelijkheid van denkbeeldig deel van diëlektrische permittiviteit voor MCC-monsters met verschillende waterinhoud

Voor een ontspanningsproces bij benadering van één keer ontspanning (τ = τ ₀ exp((U − TΔS )/kT ) en onder voorwaarde van maximale afhankelijkheid van het imaginaire deel van complexe diëlektrische permittiviteit (ε ′ ′ (T , f )) ωτ = 1_, veranderingen van entropie ΔS /k (zie Fig. 14) en activeringsenergie U (zie Fig. 14) met waterconcentratie werden verkregen.

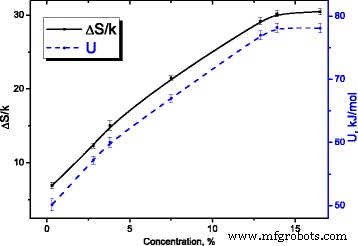
Afhankelijkheden van de entropie en de activeringsenergie van het relaxatieproces van de waterconcentratie in MCC. Afhankelijkheden van de entropie en de activeringsenergie van het relaxatieproces van de waterconcentratie in MCC

We nemen aan dat entropie van activering van het relaxatieproces verband houdt met de kans op vorming van waterstofbruggen van een methylolgroep met omringende watermoleculen [18].

Zijn groei getuigt van de toename van het gemiddelde aantal watermoleculen die deze groepen op het oppervlak van MCC-kristallieten omringen.

De verzadiging van de afhankelijkheid ∆S/k (zie Fig. 14) bij groei van de waterconcentratie is een gevolg van de vorming van een vaste hydraatschil in het systeem van MCC-kristallieten als gevolg van de opname van afzonderlijke oppervlakteclusters van watermoleculen na het bereiken van hun drempelconcentratie, die wordt bepaald door beschikbaar waterspecifiek oppervlak van het MCC-kristallietensysteem tijdens hun zwelling.

De groei van activeringsenergie U (C ) van het relaxatieproces (zie Fig. 14) en verzadiging van de afhankelijkheid van de waterconcentratie heeft dezelfde aard als voor entropie-activering is een indicatie van het structureren van het oppervlak van MCC-kristallieten tijdens de vorming van hun vaste hydraatschil.