Gelijktijdige vergelijkingen oplossen:de substitutiemethode en de optelmethode

Wat zijn simultane vergelijkingen en stelsels van vergelijkingen?

De termen gelijktijdige vergelijkingen en stelsels van vergelijkingen verwijzen naar omstandigheden waarbij twee of meer onbekende variabelen aan elkaar gerelateerd zijn via een gelijk aantal vergelijkingen.

Voorbeeld:

Voor deze reeks vergelijkingen is er maar een enkele combinatie van waarden voor x en j dat zal beide bevredigen.

Elke vergelijking, afzonderlijk beschouwd, heeft een oneindige waarde van (x,y) oplossingen, maar samen er is maar een. Uitgezet in een grafiek wordt deze voorwaarde duidelijk:

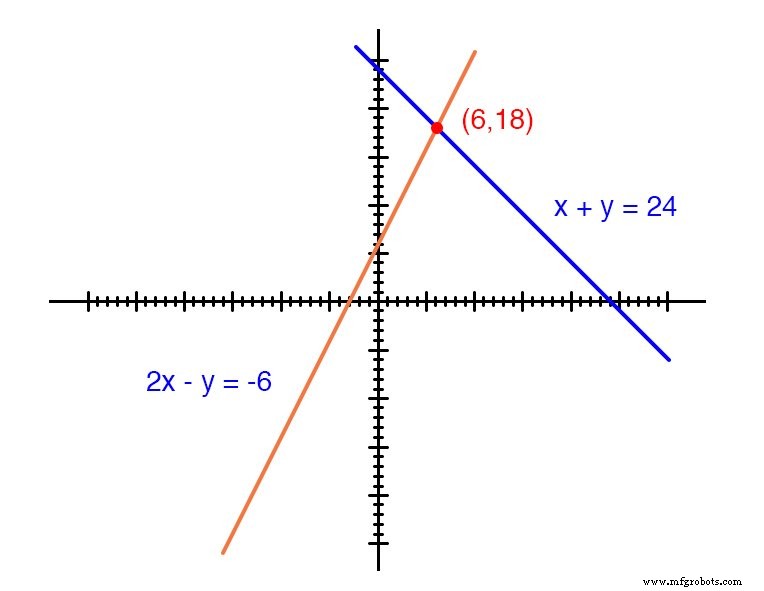
Elke lijn is eigenlijk een continuüm van punten die mogelijke x . voorstellen en j oplossingsparen voor elke vergelijking.

Elke vergelijking heeft afzonderlijk een oneindig aantal geordende paar (x ,j ) oplossingen. Er is maar één punt waar de twee lineaire functies x + y =24 en 2x - y =-6 snijden (waar een van hun vele onafhankelijke oplossingen toevallig werkt voor beide vergelijkingen), en dat is waar x is gelijk aan een waarde van 6 en y is gelijk aan een waarde van 18.

Meestal is grafieken echter geen erg efficiënte manier om de gelijktijdige oplossing voor twee of meer vergelijkingen te bepalen. Het is vooral onpraktisch voor systemen met drie of meer variabelen.

In een systeem met drie variabelen zou de oplossing bijvoorbeeld worden gevonden door het snijpunt van drie vlakken in een driedimensionale coördinatenruimte - geen eenvoudig scenario om te visualiseren.

Gelijktijdige vergelijkingen oplossen met behulp van de substitutiemethode

Er bestaan ​​verschillende algebraïsche technieken om gelijktijdige vergelijkingen op te lossen.

Misschien wel het gemakkelijkst te begrijpen is de vervanging methode.

Neem bijvoorbeeld ons voorbeeldprobleem met twee variabelen:

In de substitutiemethode manipuleren we een van de vergelijkingen zodat de ene variabele wordt gedefinieerd in termen van de andere:

Vervolgens nemen we deze nieuwe definitie van één variabele en vervangen het voor dezelfde variabele in de andere vergelijking.

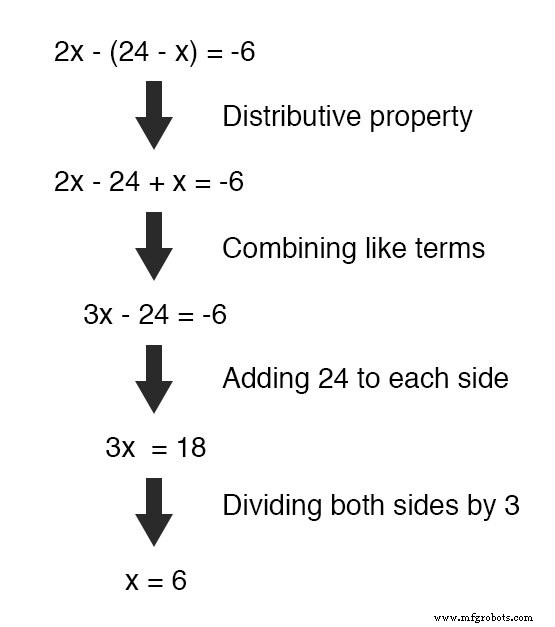
In dit geval nemen we de definitie van y , dat is 24 - x en vervang dit door y term gevonden in de andere vergelijking:

Nu we een vergelijking hebben met slechts een enkele variabele (x ), kunnen we het oplossen met behulp van "normale" algebraïsche technieken:

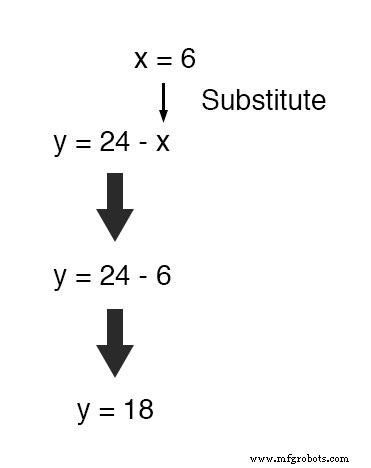
Nu dat x bekend is, kunnen we deze waarde in een van de originele vergelijkingen stoppen en een waarde voor y verkrijgen.

Of, om ons wat werk te besparen, kunnen we deze waarde (6) invoegen in de vergelijking die we zojuist hebben gegenereerd om y te definiëren in termen van x , omdat het al in een vorm is om op te lossen voor y :

Het toepassen van de substitutiemethode op systemen van drie of meer variabelen brengt een soortgelijk patroon met zich mee, alleen met meer werk.

Dit geldt over het algemeen voor elke oplossingsmethode:het aantal stappen dat nodig is om oplossingen te verkrijgen, neemt snel toe met elke extra variabele in het systeem.

Om drie onbekende variabelen op te lossen, hebben we ten minste drie vergelijkingen nodig. Beschouw dit voorbeeld:

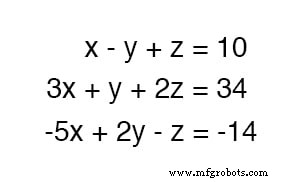
Omdat de eerste vergelijking de eenvoudigste coëfficiënten heeft (1, -1 en 1, voor x , j , en z , respectievelijk), lijkt het logisch om het te gebruiken om een ​​definitie van de ene variabele te ontwikkelen in termen van de andere twee.

Oplossen voor x in termen van y en z :

Nu kunnen we deze definitie van x . vervangen waar x verschijnt in de andere twee vergelijkingen:

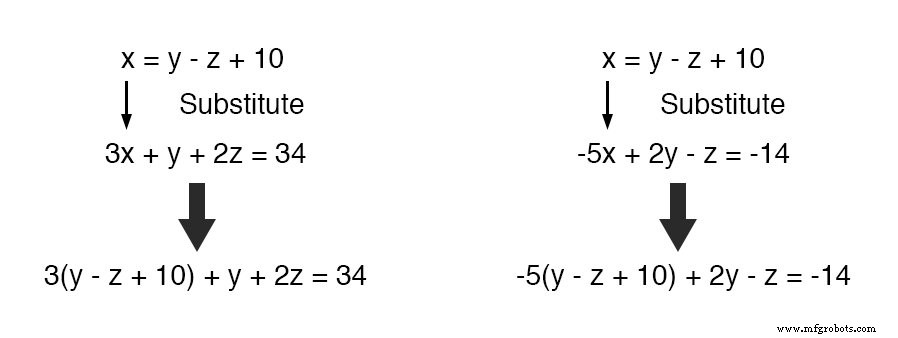
Deze twee vergelijkingen terugbrengen tot hun eenvoudigste vorm:

Tot nu toe hebben onze inspanningen het systeem teruggebracht van drie variabelen in drie vergelijkingen naar twee variabelen in twee vergelijkingen.

Nu kunnen we de substitutietechniek opnieuw toepassen op de twee vergelijkingen 4y - z =4 en -3y + 4z =36 op te lossen voor y of z . Eerst zal ik de eerste vergelijking manipuleren om z . te definiëren in termen van y :

Vervolgens vervangen we deze definitie van z in termen van y waar we z . zien in de andere vergelijking:

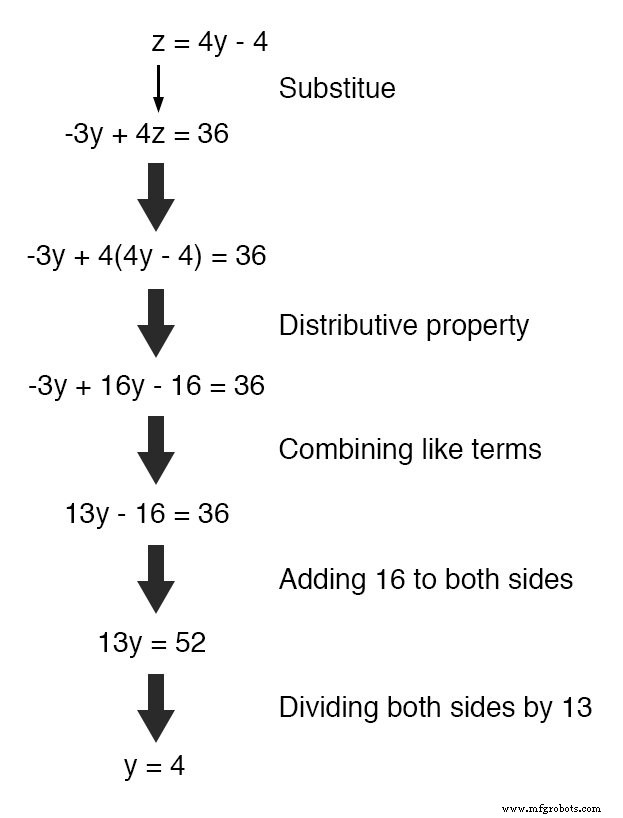
Nu dat j een bekende waarde is, kunnen we deze invoegen in de vergelijking die z . definieert in termen van y en verkrijg een cijfer voor z :

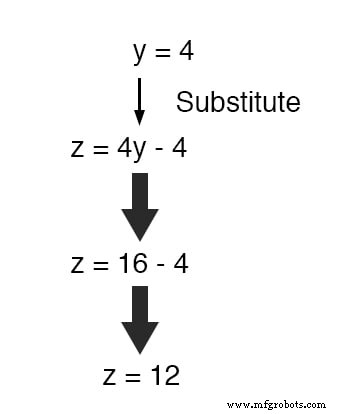
Nu, met waarden voor y en z bekend zijn, kunnen we deze invoegen in de vergelijking waar we x . hebben gedefinieerd in termen van y en z , om een ​​waarde te verkrijgen voor x :

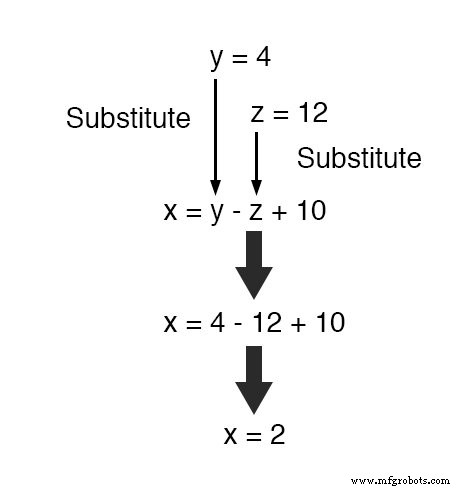
Tot slot hebben we waarden gevonden voor x , j , en z van respectievelijk 2, 4 en 12 die aan alle drie de vergelijkingen voldoen.

Gelijktijdige vergelijkingen oplossen met de optelmethode

Hoewel de vervangingsmethode op conceptueel niveau misschien het gemakkelijkst te begrijpen is, zijn er andere oplossingsmethoden voor ons beschikbaar.

Eén zo'n methode is de zogenaamde toevoeging methode, waarbij vergelijkingen bij elkaar worden opgeteld om variabele termen te annuleren.

Laten we ons systeem met twee variabelen nemen dat wordt gebruikt om de substitutiemethode te demonstreren:

Een van de meest gebruikte regels van de algebra is dat je elke rekenkundige bewerking die je wilt op een vergelijking mag uitvoeren, zolang je het maar gelijk aan beide kanten doet. .

Met betrekking tot optellen betekent dit dat we elke gewenste hoeveelheid aan beide zijden van een vergelijking kunnen toevoegen, zolang het maar hetzelfde is. hoeveelheid — zonder de waarheid van de vergelijking te veranderen.

Een optie die we dan hebben, is om de corresponderende zijden van de vergelijkingen bij elkaar op te tellen om een ​​nieuwe vergelijking te vormen.

Aangezien elke vergelijking een uitdrukking is van gelijkheid (dezelfde hoeveelheid aan weerszijden van de = teken), is het toevoegen van de linkerkant van de ene vergelijking aan de linkerkant van de andere vergelijking geldig zolang we de rechterkant van de twee vergelijkingen ook bij elkaar optellen.

In onze voorbeeldvergelijkingsset kunnen we bijvoorbeeld x + y . toevoegen tot 2x - y en voeg 24 . toe en -6 ook samen om een ​​nieuwe vergelijking te vormen.

Welk voordeel heeft dit voor ons? Onderzoek wat er gebeurt als we dit doen met onze voorbeeldvergelijkingsset:

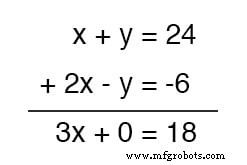
Omdat de bovenste vergelijking toevallig een positieve y . bevatte term terwijl de onderste vergelijking toevallig een negatieve y . bevatte term, annuleerden deze twee termen elkaar tijdens het toevoegen, waardoor er geen y . overbleef termijn in de som.

Wat we nog hebben is een nieuwe vergelijking, maar wel een met slechts een enkele onbekende variabele, x ! Dit stelt ons in staat om eenvoudig de waarde van x . op te lossen :

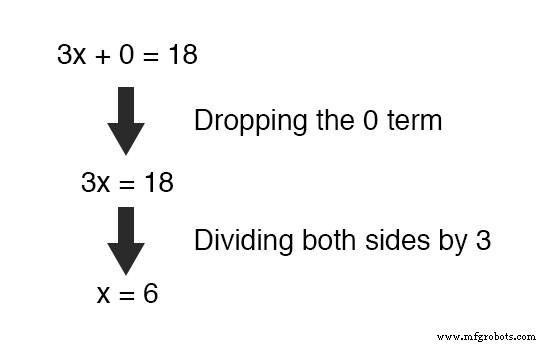
Zodra we een bekende waarde hebben voor x , natuurlijk, bepalen y 's waarde is gewoon een kwestie van vervanging (vervanging van x met het cijfer 6 ) in een van de originele vergelijkingen.

In dit voorbeeld werkte de techniek van het bij elkaar optellen van de vergelijkingen goed om een ​​vergelijking te produceren met een enkele onbekende variabele.

Hoe zit het met een voorbeeld waar dingen niet zo eenvoudig zijn? Beschouw de volgende verzameling vergelijkingen:

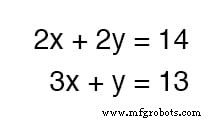
We zouden deze twee vergelijkingen bij elkaar kunnen optellen - dit is een volledig geldige algebraïsche bewerking - maar het zou ons niet helpen om waarden te verkrijgen voor x en j :

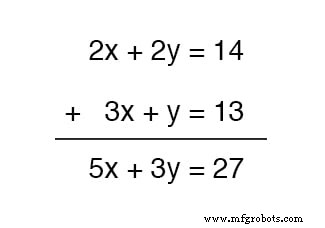
De resulterende vergelijking bevat nog steeds twee onbekende variabelen, net als de oorspronkelijke vergelijkingen, en dus zijn we niet verder met het verkrijgen van een oplossing.

Wat als we echter een van de vergelijkingen zouden kunnen manipuleren om een ​​negatieve term te hebben die zou annuleer de respectieve term in de andere vergelijking wanneer toegevoegd?

Dan zou het systeem reduceren tot een enkele vergelijking met een enkele onbekende variabele, net als bij het laatste (toevallige) voorbeeld.

Als we de y . maar konden draaien term in de onderste vergelijking in een - 2y term, zodat wanneer de twee vergelijkingen bij elkaar worden opgeteld, beide y termen in de vergelijkingen zouden annuleren, waardoor we alleen een x . overhouden termijn zou dit ons dichter bij een oplossing brengen.

Gelukkig is dit niet moeilijk om te doen. Als we vermenigvuldigen elke term van de onderste vergelijking met een -2 , het zal het resultaat opleveren dat we zoeken:

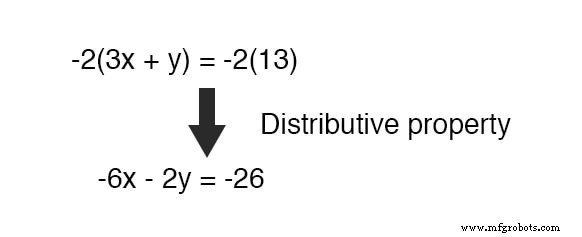
Nu kunnen we deze nieuwe vergelijking toevoegen aan de oorspronkelijke, bovenste vergelijking:

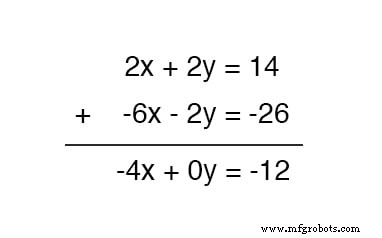
Oplossen voor x , verkrijgen we een waarde van 3 :

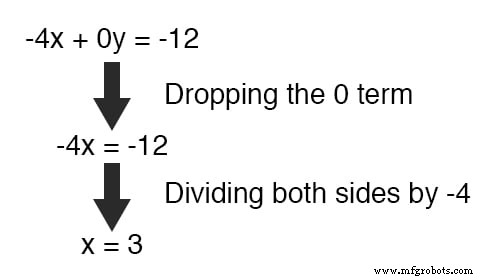
Deze nieuw gevonden waarde vervangen door x in een van de oorspronkelijke vergelijkingen, de waarde van y is gemakkelijk te bepalen:

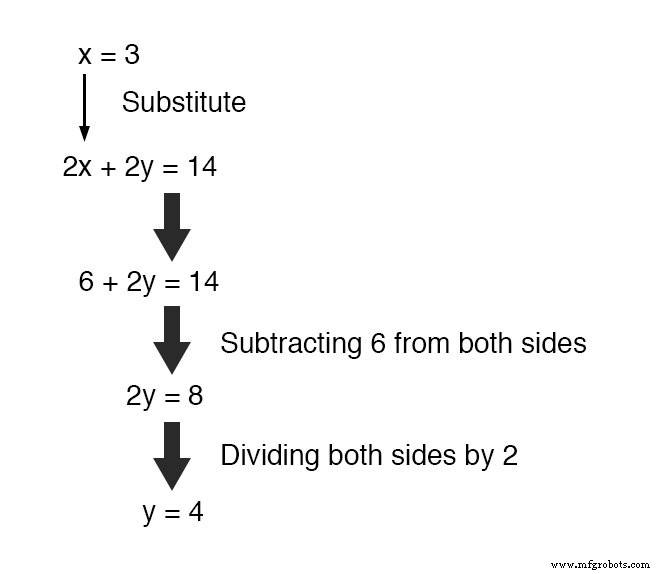
Het gebruik van deze oplossingstechniek op een systeem met drie variabelen is iets ingewikkelder.

Net als bij substitutie moet u deze techniek gebruiken om het drievergelijkingssysteem van drie variabelen terug te brengen tot twee vergelijkingen met twee variabelen, en deze vervolgens opnieuw toepassen om een ​​enkele vergelijking met één onbekende variabele te verkrijgen.

Om te demonstreren, gebruik ik het drie-variabele vergelijkingssysteem uit de substitutiesectie:

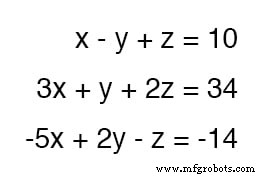
Omdat de bovenste vergelijking coëfficiëntwaarden heeft van 1 voor elke variabele is het een gemakkelijke vergelijking om te manipuleren en te gebruiken als een annuleringshulpmiddel.

Als we bijvoorbeeld de 3x . willen annuleren term uit de middelste vergelijking, alles wat we hoeven te doen is de bovenste vergelijking nemen, elk van zijn termen vermenigvuldigen met -3 , en voeg het dan als volgt toe aan de middelste vergelijking:

We kunnen de onderste vergelijking van zijn -5x term op dezelfde manier:neem de oorspronkelijke bovenste vergelijking, vermenigvuldig elk van zijn termen met 5 , voeg dan die gewijzigde vergelijking toe aan de onderste vergelijking, zodat er een nieuwe vergelijking overblijft met alleen y en z voorwaarden:

Op dit punt hebben we twee vergelijkingen met dezelfde twee onbekende variabelen, y en z :

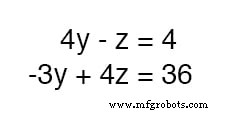
Bij inspectie zou het duidelijk moeten zijn dat de -z term van de bovenste vergelijking kan worden gebruikt om de 4z . te annuleren term in de onderste vergelijking als we elke term van de bovenste vergelijking maar vermenigvuldigen met 4 en tel de twee vergelijkingen bij elkaar op:

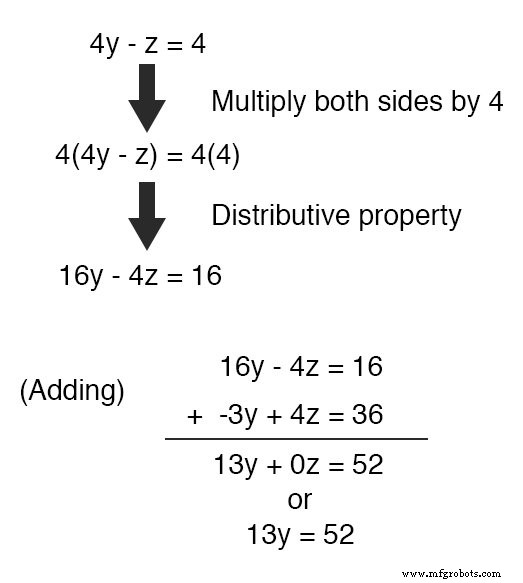
De nieuwe vergelijking nemen 13y =52 en oplossen voor y (door beide zijden te delen door 13 ), krijgen we een waarde van 4 voor j .

Vervanging van deze waarde van 4 voor j in een van de twee-variabele vergelijkingen kunnen we oplossen voor z .

Beide waarden van y . vervangen en z in een van de oorspronkelijke vergelijkingen met drie variabelen kunnen we oplossen voor x .

Het eindresultaat (ik zal je de algebraïsche stappen besparen, aangezien je ze inmiddels wel zou moeten kennen!) is dat x =2 , y =4 , en z =12 .

GERELATEERDE WERKBLAD:

• Gelijktijdige vergelijkingen voor het werkblad voor circuitanalyse