Een WS2-case-theoretisch onderzoek:waterstofopslagprestaties verbeterd door faseverandering
Abstract
Waterstof is een schone energie met een hoog rendement, terwijl de opslag- en transportproblemen grootschalig gebruik ervan nog in de weg staan. Vanwege het grote specifieke oppervlak en de unieke elektronische structuur hebben tweedimensionale materialen een groot potentieel in waterstofopslag. In het bijzonder monolaag 2H-WS2 geschikt is gebleken voor waterstofopslag. Maar er zijn weinig studies over de andere twee fasen van WS2 (1T, 1T′) in waterstofopslag. Hier hebben we eerste-principeberekeningen uitgevoerd om het waterstofadsorptiegedrag van alle drie de fasen van WS2 te onderzoeken. . Meerdere waterstofadsorptiestudies evalueren ook de waterstofopslagcapaciteiten van deze materialen. Uitgebreide analyseresultaten laten zien dat de 1T′-WS2 heeft betere waterstofopslagprestaties dan de 2H-WS2 , wat betekent dat fase-engineering een effectieve manier kan zijn om de prestaties van waterstofopslag te verbeteren. Dit artikel biedt een referentie voor de verdere studie van waterstofopslag in tweedimensionale materialen.
Inleiding
Conventionele waterstofopslag brengt een aanzienlijk risico met zich mee vanwege de lage ontsteking, de brede brandbaarheid en de brosheid op staal [1, 2]. Hoewel metaalhydriden, zoals CaH2 , grote hoeveelheden waterstof kunnen opslaan, zijn ze niet alleen ontvlambaar als ze nat zijn, maar ook duur en moeilijk te hergebruiken. Daarom is de zoektocht naar een veilig, economisch en effectief waterstofopslagmateriaal een wijdverbreide zorg geworden [3]. Vanwege hun grote specifieke oppervlak en unieke elektronische eigenschappen zijn tweedimensionale (2D) materialen op grote schaal gebruikt in veel gebieden, zoals fotokatalytische watersplitsing, waterstofevolutiereactie, transistors, elektroluminescente apparaten, gasopslag en gasadsorptie [4, 5,6,7,8,9]. Waterstof die op grafeen adsorbeert, houdt bijvoorbeeld de herhybridisatie van koolstofvalentie-orbitalen in door C-C π te transformeren binding aan C–H σ binding, die de bandgap en het magnetische moment rond het Fermi-niveau zou kunnen induceren, zodat hydrogenering van grafeen een opwindende mogelijkheid biedt om elektronische circuits op atomaire schaal direct te schrijven met vooraf ontworpen patronen [10]. Het succes van op grafeen gebaseerde materialen heeft ook geleid tot onderzoek naar andere 2D-materialen die worden toegepast bij gasadsorptie of -opslag [11,12,13,14]. Wat nog belangrijker is, is dat monolaag overgangsmetaaldisulfide (TMD) materialen met name uitstekende prestaties hebben laten zien bij waterstofopslag [15].
De capaciteit voor waterstofopslag kan worden beoordeeld aan de hand van de adsorptiesterkte van de gasmoleculen over het oppervlak van het materiaal [16]. De adsorptiesterkte mag niet te sterk of te zwak zijn omdat de doelgasmoleculen moeilijk te scheiden zijn van het materiaal onder sterke adsorberende kracht of onstabiel geadsorbeerd worden onder zwakke adsorberende kracht [17]. De gemiddelde bindingsenergieën per waterstofmolecuul van geschikte waterstofopslagmaterialen is van -0,2 tot -0,6 eV bij kamertemperatuur (ongeveer 25 °C) [12]. Originele materialen zoals grafeen of TMD's hebben echter een tekortkoming dat hun bindingskracht aan waterstofmoleculen te zwak is [18, 19]. Oppervlaktefunctionaliseringsmethoden werden meestal gebruikt om hun waterstofadsorberende eigenschappen te verbeteren. Door een doterings- of decoratieproces kunnen de oppervlakte-eigenschappen van 2D-materialen worden aangepast aan het bereik van matige waterstofadsorptie-energie, en de waterstofopslagprestaties kunnen verder worden verbeterd [20]. Het is echter moeilijk om de stabiliteit van decoratiesystemen te behouden [21, 22]. En het is een uitdaging om nauwkeurig te dopen of te decoreren [23]. Dergelijke methoden zijn theoretisch haalbaar, maar verre van toepassingen.
Als typische TMD's, MoS2 en WS2 hebben hun uitstekende toepassingspotentieel op het gebied van waterstofopslag bewezen [24, 25]. Vanwege zijn superieure katalytische prestaties en unieke elektrische eigenschappen, MoS2 maakt zich op veel gebieden grote zorgen [26], en WS2 wordt vaak over het hoofd gezien. Vergeleken met enkellaagse MoS2 , WS2 heeft een betere thermische stabiliteit [27, 28] en een grotere bindingsenergie met waterstofmoleculen onder compressiespanning [29]. Het is bekend dat WS2 heeft ook twee andere fasen (1T/1T′), die verschillende symmetrieën en verschillende elektronische eigenschappen hebben. Eerdere studies hebben aangetoond dat ze met eenvoudige methoden kunnen worden bereid [30, 31]. De meeste methoden waren gebaseerd op faseovergang van 2H fase WS2 en gecombineerd met stabilisatiemanieren. Veel studies hebben een succesvolle voorbereiding van hoog percentage en stabiele 1T/1T′-WS2 . aangetoond (Tabel S1). Onlangs is de metalen 1T-WS2 en zijn vertakking 1T′-WS2 hebben een groot potentieel aangetoond in toepassingen van waterstofevolutiereactie (HER) [23, 32]. De onderzoeksresultaten toonden aan dat hun oppervlak een matige adsorptiesterkte heeft aan het reactietussenproduct H*. Dat maakt de weg vrij voor hun andere toepassingen die verband houden met de adsorptie van waterstof, zoals waterstofopslag. Er zijn echter weinig studies over waterstofopslageigenschappen van deze twee fasen van WS2 . De effecten van faseverschil op waterstofopslag zijn altijd genegeerd.
In dit werk hebben we alle drie de fasen van WS2 . onderzocht om hun geschiktheid als waterstofopslagmateriaal te vergelijken. We voerden een systematische theoretische studie uit van de structuren en analyseerden de adsorptie-energie en adsorptieconfiguratie van gasmoleculen. Om echte werkomstandigheden te simuleren, werd de adsorptie van talrijke waterstofmoleculen bestudeerd. Met de berekeningsresultaten in dit werk, vonden we dat 1T′-WS2 is de beste kandidaat van deze drie fasen van WS2 als waterstofopslagmateriaal. De fase van WS2 wijzigen geeft een verbetering in waterstofopslag. Het kan dus een referentie vormen voor het onderzoek naar waterstofopslag door tweedimensionale materialen met het oog op fase.
Berekeningsdetails
De eerste principes werden gebruikt op basis van de dichtheidsfunctionaaltheorie (DFT). Alle berekeningen in dit werk zijn uitgevoerd in Dmol3 [33]. De lokale dichtheidsbenadering (LDA) wordt gebruikt om uitwisselings- en correlatiepotentialen met de PWC-functie te verwerken. Het enkele productieve potentieel werd gebruikt om de kernel (DFT semi-core pseudopots) te vervangen om de rekenkosten te verlagen. Hogere nauwkeurigheid werd bereikt door een dubbele numerieke orbitale basisset en orbitale polarisatiefunctie (DNP) te kiezen. Vervolgens werd een convergentietest gegeven. Na de test, de Monkhorst-Pack k -punten was ingesteld op 4 × 4 × 1, maak vervolgens een vacuümlaag van 20 Å om interacties tussen de lagen te voorkomen. De precisie van de energieconvergentie was ingesteld op 1 × 10 −5 Hartree (1 Hartree =27,212 eV), de maximale verplaatsing was 0,005 Å en de atomaire krachten waren niet meer dan 0,002 Hartree/Å. Alle latere berekeningen volgen deze eigenschappen.
Voor deze drie fasen van WS2 (1T/1T′/2H), de rekenmodellen waren supercellen van 4 × 4 monolaag WS2 . De 1T-WS2 en 2H-WS2 constructies werden eerst door onszelf gebouwd. Nadat de constructie is voltooid, wordt geometrische optimalisatie uitgevoerd, inclusief unit-optimalisatie. En de 1T′-WS2 werd gebouwd op basis van de bestaande 1T′-MoS2 . Terwijl de 1T′-MoS2 werd gebouwd op basis van een 2 × 2 1T-model, een enkel waterstofatoom werd een sleutelverbinding met een S-atoom van de 1T MoS2 . Vervolgens kreeg het systeem een andere geometrie-optimalisatie. Na optimalisatie werden de waterstofatomen verwijderd en opnieuw geoptimaliseerd om de reguliere 1T′-MoS2 te verkrijgen structuur. Daarna werden alle Mo-atomen vervangen door W-atomen in een 2 × 2-model, en ondergingen vervolgens een geometrie-optimalisatie, inclusief celoptimalisatie opnieuw.
Met de geoptimaliseerde 2 × 2 WS2 model, een supercel van 4 × 4 monolaag WS2 werd gebouwd. Zoals getoond in figuur S1, de modellen van al deze drie fasen van WS2 bevatten 32 S-atomen en 16 W-atomen in een cel. Omdat 16 van de 25 W-atomen in het 1T-fasemodel zich op de plaatsen van de rand of hoek bevinden, is de geldige hoeveelheid W-atomen in de cel nog steeds 16. De bindingen tussen elke W-atomen in het 1T- of 2H-model zijn gelijk, terwijl die in 1T′-WS2 zijn niet gelijk. Met de W–W binding in 1T′-WS2 , de opstelling van de W atomen lijkt op een zigzag-keten.
Daarom wordt de 1T′-fase in sommige onderzoeken ook wel de zigzag-ketenfase genoemd. We kunnen herhalende eenheden vinden in de drie structuren die tekens gemeen hebben. Zoals getoond in de illustraties van Fig. 1, vertegenwoordigen de groene vakken de herhalende eenheden met alleen W-atomen aan de rand, terwijl de rode die zijn die zijn omlijnd door S-atomen. Vanwege het symmetrieverschil is de grootte van de groene doos in het 1T′-model bijna twee keer zo groot als die in het 1T-model. De rode doos in 1T- of 1T′-modellen is een zeshoek, maar in het 2H-model is het een driehoek. Er zijn ook soortgelijke herhalende eenheden in 1T en 1T′-WS2 structuren, zoals het blauwe rechthoekige gebied in figuur S1. Bovendien zijn de axisymmetrische elementen die in de rode vakken in de 1T- en 1T′-modellen worden weergegeven, ook te vinden in figuur S1 en dat zou ook de symmetrie van 1T en 1T′-WS kunnen vertegenwoordigen2 structuur.
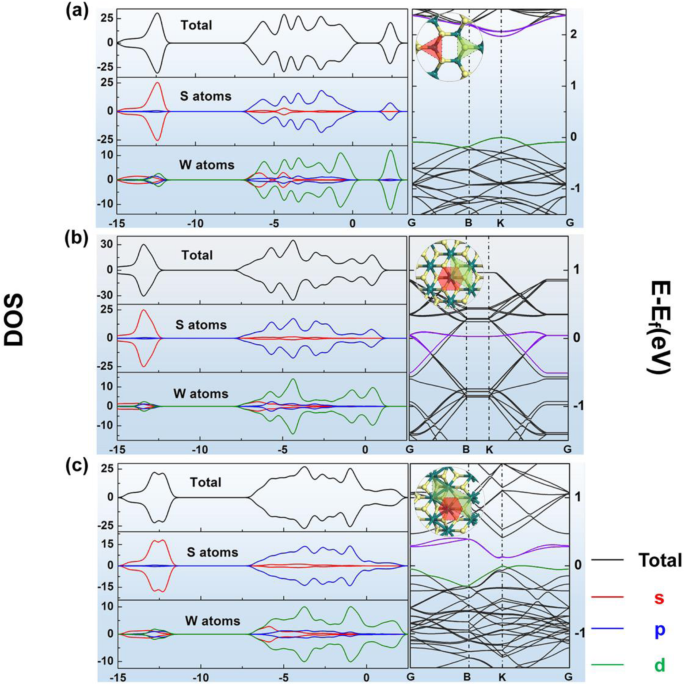
Resultaten van geometriestructuur, DOS en bandstructuur van a 2H-WS2 , b 1T-WS2 , en c 1T′-WS2; gele ballen vertegenwoordigen S, en glaucous ballen vertegenwoordigen W
Een enkel waterstofmolecuul werd op de c . geplaatst -as boven de WS2 vlak om een waterstofadsorptiemodel op te stellen, en verschillende adsorptieplaatsen met een hoge geometrische symmetrie werden geselecteerd. Voor het geval van 1T-WS2 getoond in figuur S2 (b) en (e), waren er vijf locaties:net boven het S-atoom van de bovenste laag, net boven het S-atoom van de onderste laag, net boven het W-atoom, boven de binding van het W-atoom, en de bovenste laag S-atoom, boven de binding van W-atoom en onderste laag S-atoom. En voor 1T′-WS2 , deze zes situaties werden getoond in figuur S2 (c) en (f). Voor 2H-WS2 getoond in figuur S2 (a) en (d), waren er vier situaties:net boven de S-atoomplaats, net boven de W-atoomplaats, boven het midden van de W-atoom- en S-atoomplaats, en precies boven het midden van de zeshoekige structuur. Deze locaties zijn gekozen omdat het zeer symmetrische locaties van deze materialen zijn. Na gegeven geometrie-optimalisaties en vergelijking van adsorptie-energie, konden stabiele adsorptiesites worden gevonden. En we onderscheidden de houding van het waterstofmolecuul geadsorbeerd op de 1T′-WS2 vanwege de relatief lagere structurele symmetrie. De waterstofmoleculen werden horizontaal of verticaal geplaatst (zoals weergegeven in figuur S3), wat de situatie verdubbelde. Na de optimalisatie van de geometrie wordt alle adsorptie-energie weergegeven in tabel S2. De meest stabiele adsorptieplaatsen werden gekozen op basis van de resultaten van de adsorptie-energie. Voor het waterstofadsorptieproces wordt de adsorptie-energie berekend met de volgende functie:E advertentie =E tot − E mat − E hyd , waar E tot is de totale energie van elk van deze drie fasen van WS2 met de waterstofmoleculen geadsorbeerd, E mat (energie van het materiaal) vertegenwoordigt de totale energie van ongerepte WS2 , en E hyd vertegenwoordigt de totale energie van een geïsoleerd waterstofmolecuul. Volgens deze relatie, een hogere absolute waarde van E advertentie leidt tot meer stabiliteit van het adsorptiesysteem. De werkende kracht tussen de materialen en de doelgasmoleculen kan ook worden weerspiegeld door de absolute waarde van E advertentie . Een afstotende kracht wordt weergegeven door een positieve waarde van E advertentie , terwijl een negatieve waarde een aantrekkingskracht weerspiegelt. Hoewel de exacte adsorptie-energie niet via deze methode kon worden verkregen [34], kan het de vorm en sterkte van de interactie tussen waterstof en adsorberend materiaal weerspiegelen. Zoals hierboven geïntroduceerd, is de ideale adsorptie-energie voor waterstofopslagtoepassingen voor elk waterstofmolecuul − 0,2 tot − 0,6 eV/H2 bij kamertemperatuur [35].
Resultaten en discussie
Voor alle modellen van deze materialen konden de structuren met de laagste energie worden gevonden na de optimalisatie van de geometrie. De lengtes van alle W-S-bindingen in monolaag 1T-WS2 en 2H-WS2 zijn respectievelijk 2,428 Å en 2,402 Å. Maar die in de 1T′-WS2 zijn ongelijk, met een lengte van ongeveer 2,453 Å, 2,410 Å en 2,490 Å. Er kan ook worden vastgesteld dat W-W-bindingen in het geoptimaliseerde 1T′-model een lengte hebben van ongeveer 2,784 Å. Bandstructuren van al deze drie fasen van geoptimaliseerde ongerepte WS2 worden getoond in Fig. 1. Voor de metalen 1T-fase is er geen bandgap. En voor de 1T′-fase heeft het een semi-metalen bandstructuur. In de 2H-fase komt de bandstructuur overeen met het kenmerk van een halfgeleider. De partiële toestandsdichtheid (PDOS) van deze drie modellen wordt ook getoond in Fig. 1. Uit de PDOS-resultaten blijkt dat de vorm van Sp- en Wd-banen het meest overeenkomt met die van de totale DOS in al deze drie figuren , wat aangeeft dat Sp- en Wd-banen hebben bijgedragen aan de totale DOS, meestal voor al deze drie fasen van WS2 . De tendens van de DOS-resultaten van 1T′-WS2 is in overeenstemming met de bandstructuur en komt overeen met de vorige studie [32]. De verschillende posities van geabsorbeerde waterstofmoleculen werden vergeleken om de meest stabiele te vinden in al deze drie modellen. Posities werden gekozen volgens de E advertentie en Hirschfeld laden de resultaten van de genoemde situaties over de geabsorbeerde enkelvoudige waterstofmoleculen in de structuren van deze drie fasen (de E advertentie en Hirschfeld-laadresultaten worden getoond in Fig. 2a-c en Tabel S2). Voor 1T WS2 , het is site 3, en voor 1T′-WS2 , het is site 1 (zoals getoond in Fig. 2b, c), terwijl voor 2H-WS2 , het is site 3 (allemaal getoond in Fig. 2a en Tabel S2-S3). Op basis van deze resultaten, ten eerste, 1T fase WS2 is niet geschikt voor waterstofadsorptie omdat de E advertentie voor waterstof op 1T WS2 is veel significanter dan 0,6 eV (tabel S2). Dat betekent dat het te moeilijk zal zijn om de geadsorbeerde waterstofmoleculen uit de 1T WS2 oppervlakte. Volgens dit resultaat zouden de volgende onderzoeken zich niet over deze fase moeten bekommeren. De E advertentie de resultaten van de 1T′-fase en de 2H-fase liggen rond de − 0,27 eV, beide in het toepasselijke adsorptie-energiebereik voor waterstofopslagtoepassingen.
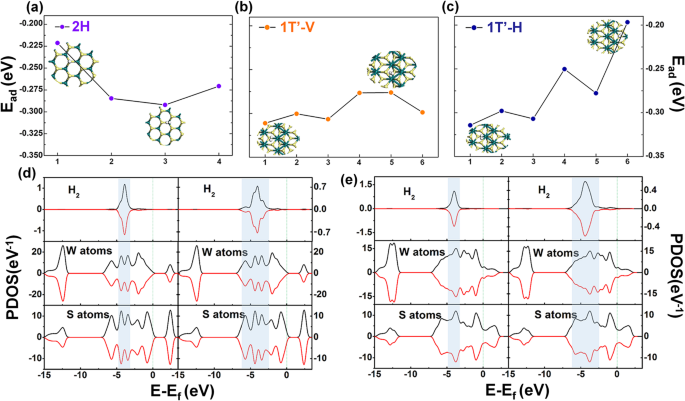
Adsorptie-energieresultaten van H2 adsorptiesysteem voor a enkele H2 op 2H-WS2, b en c enkele H2 op 1T'-WS2; PDOS-resultaten van de situatie met de laagste (links) of de hoogste (rechts) Eadvertentie in d 2H-modellen en dat in e 1T'-model
Om deze twee fasen verder te vergelijken, werd de PDOS-analyse uitgevoerd, die wordt getoond in Fig. 2d, e. De linkerdelen tonen de laagste PDOS-adsorptie-energieën van de twee fasen, terwijl de rechterdelen de twee hoogste zijn. Er zijn kleine verschillen in beide situaties van de laagste of de hoogste energie. In het linkerdeel van figuur 2d, e (wat overeenkomt met de laagste adsorptie-energie), liggen de hoofdpieken beide op -3 tot -5 eV. Terwijl het voor het rechterdeel (dat de hoogste adsorptie-energie vertegenwoordigt), tussen − 2,5 en − 6 eV leek. Dit uiterlijk betekent dat er een grotere superpositie is tussen de PDOS van het waterstofmolecuul en WS2 , wat wijst op een sterkere interactie tussen hen. Deze resultaten komen goed overeen met de adsorptie-energieresultaten. De PDOS-resultaten voor situaties met één waterstofmolecuul konden echter nog steeds niet goed het verschil in waterstofadsorptie-eigenschappen tussen deze twee soorten materialen weerspiegelen.
Daarom hebben we onderzoek gedaan naar verschillende aantallen waterstofmoleculen die zijn geadsorbeerd op het oppervlak van zowel 1T′ als 2H-WS2 . Zoals figuur S4 laat zien, plaatsen we verschillende aantallen waterstofmoleculen (16, 32, 48 en 64) op het oppervlak van zowel 1T′ als 2H-WS2 . Voor 1T′-WS2 , wanneer het aantal waterstofmoleculen minder dan 16 is, wordt elk van de waterstofmoleculen in de meest stabiele positie geplaatst (site 1v). Gezien de invloed van de mogelijke interactie tussen meerdere H2 moleculen, bespraken we verder de rangschikking van H2 wanneer 2 of 3 H2 moleculen geadsorbeerd 1T′-WS2 . Voor twee waterstofmoleculen hebben we drie situaties overwogen:aangrenzende locaties (2H2 -1), op afzonderlijke plaatsen aan dezelfde kant (2H2 -2), en op de dichtstbijzijnde locaties van verschillende kanten (2H2 -3) Voor drie waterstofmoleculen waren er vijf gevallen:drie aangrenzende plaatsen aan dezelfde kant (3H2 -1); twee aangrenzende en één gescheiden, allemaal aan dezelfde kant (3H2 -2); drie gescheiden aan dezelfde kant (3H2 -3); twee buren aan dezelfde kant en één aan de andere kant (3H2 -4); en twee gescheiden aan dezelfde kant en één aan de andere kant (3H2 -5). De berekende adsorptie voor elk geval werd vergeleken (Tabel S4). De resultaten laten zien dat het plaatsen van waterstofmoleculen op aangrenzende plaatsen van 1T′-WS2 zou de totale adsorptie-energie groter maken dan afzonderlijke gevallen. Dat betekent dat er een onregelmatige verandering van de adsorptie-energie zal optreden als H2 moleculen werden willekeurig geplaatst, zelfs op dezelfde adsorptieplaats. Er was echter geen duidelijke invloed wanneer waterstofmoleculen werden geplaatst op de dichtstbijzijnde plaatsen van verschillende zijden van 1T′-WS2 . Op basis van deze resultaten worden waterstofmoleculen ingesteld volgens de volgende principes:wanneer H2 moleculen zijn kleiner dan 8, waterstofmoleculen zijn geplaatst op niet-aangrenzende adsorptieplaatsen aan weerszijden van 1T′-WS2; wanneer het aantal 8 tot 16 is, konden naburige sites niet worden vermeden. Aangrenzende adsorptieplaatsen worden nog zoveel mogelijk vermeden. Wanneer waterstofmoleculen tussen 17 en 32 zijn, worden 16 daarvan op de meest stabiele positie geplaatst (site 1v) en de rest verticaal boven de W-atomen (site 3v). Wanneer waterstofmoleculen meer dan 32 zijn, krijgt de afstand tussen deze waterstofmoleculen prioriteit om de vorming van waterstofmoleculaire groepen te voorkomen, zoals weergegeven in figuur S6. En dan zal de horizontale of verticale plaatsing afhangen van de adsorptie-energieresultaten van enkele waterstof. Daarom, wanneer de H2 tussen 33 en 48 ligt, bevinden de eerste 16 moleculen zich op plaats 1v, de tweede 16 moleculen bevinden zich op plaats 3v en de rest bevindt zich op plaats 4h. Als het aantal hoger is dan 48, bevinden de eerste 16 moleculen zich op plaats 1v, de tweede 16 moleculen op plaats 3v, de derde 16 moleculen op plaats 4h en de rest op plaats 2h. We proberen waterstofmoleculen gelijkmatig aan beide zijden van deze structuur te rangschikken en ervoor te zorgen dat de afstand tussen elk waterstofmolecuul ver genoeg is. In de toestand van de 2H-fase, vergelijkbaar met de gevallen van 1T′-WS2 , wanneer waterstofmoleculen lager zijn dan 32, wordt elk ingesteld op de meest stabiele positie die hierboven is besproken (site 3). Om de effecten van inconsistentie veroorzaakt door de interactie tussen waterstofmoleculen te voorkomen, werden waterstofmoleculen op niet-aangrenzende plaatsen geplaatst wanneer de hoeveelheid minder dan 16 is. Maar we moeten proberen aangrenzende plaatsen te vermijden wanneer de hoeveelheid tussen 17 en 32 ligt. tussen 33 en 64, wordt de rest in het midden van de zeshoek geplaatst (plaats 4). We proberen ook alle moleculen te verdelen volgens het hierboven vermelde principe. Anderzijds kijken we ook naar de stabiliteit van het adsorptiesysteem met een hoge concentratie H2 moleculen. Wanneer een gasmolecuul groter is dan 16, is de stabiliteit van het hele systeem ook onderzocht door moleculaire dynamica-simulaties, die wordt weergegeven in figuur S7. Na 500 stappen van simulatie van molecuuldynamica, is er geen sprake van geometrieknikken en blijft de totale energie ook bijna constant, zodat het hele systeem een grote stabiliteit heeft.
De adsorptie-energie aan de waterstofmoleculen werd berekend na een optimalisatie van de geometrie. Zoals figuur 3 laat zien, maakt het niet uit in welke fase van WS2 , neemt de totale adsorptie-energie bijna lineair toe wanneer het aantal waterstofmoleculen toeneemt. Dat betekent dat wanneer het aantal waterstofmoleculen toeneemt, de interactiekracht tussen het materiaal en de geadsorbeerde moleculen niet veel verandert. Het groene gebied in Fig. 3a geeft het gematigde waterstofadsorptie-energiegebied weer. Het kan worden gevonden dat 2H-WS2 komt eerder uit dit gebied dan de 1T′-fase. Dat betekent dat wanneer de hoeveelheid geadsorbeerd H2 moleculen worden overbodig, het zal moeilijk zijn om meer waterstofmoleculen vrij te maken uit 2H-WS2 dan van 1T′-WS2 , die een kleinere waterstofcapaciteit beoogt. Dan is ook, zoals figuur 3 laat zien, het aantal waterstofmoleculen voor de gemiddelde adsorptie-energieën van de geadsorbeerde waterstofmoleculen in het bereik van -0,2 tot -0,6 eV lager dan 48 of 55 in de situatie van 2H of 1T′ fase , respectievelijk. Dat betekent de theoretische redelijke adsorptiehoeveelheid voor waterstof op 2H-WS2 kan oplopen tot 2,4 wt%, terwijl dat in de 1T′-fase tot 2,7 wt% kan zijn. Dat onthult dat het veranderen van de fase de waterstofopslagprestaties van WS2 . kan verbeteren effectief. De gemiddelde adsorptie-energie van de twee soorten WS2 neemt af en neemt vervolgens toe wanneer het niet meer dan 8 is. Het is gemakkelijk te begrijpen dat wanneer het materiaal meer gasmoleculen adsorbeert, de gemiddelde interactiekracht tussen de gasmoleculen en het materiaal zwakker zal worden. Wanneer het aantal waterstofmoleculen echter groter is dan 8, is de reden voor de toenemende gemiddelde adsorptie-energie nog onbekend.
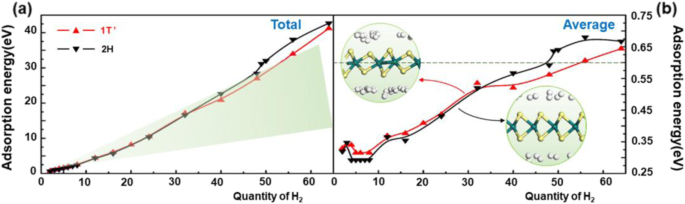
Grafieken van a totale adsorptie-energie en b gemiddelde adsorptie-energie als functie van het aantal waterstofmoleculen geabsorbeerd op de 1T'- en 2H-WS2
Voer de PDOS-studie opnieuw uit, zoals weergegeven in Fig. 4. Het blijkt dat naarmate het aantal waterstofmoleculen toeneemt, de totale PDOS van de geadsorbeerde waterstofmoleculen wordt gedispergeerd in beide fasen van WS2 (vooral wanneer het aantal waterstofmoleculen groter is dan 16). En het PDOS-bereik van enkele waterstofmoleculen die in deze systemen worden geadsorbeerd, wordt ook uitgebreider. Maar de PDOS voor de W-atomen en S-atomen blijft ongewijzigd, wat de stabiliteit van deze twee materialen vertegenwoordigt wanneer waterstofmoleculen werden geadsorbeerd. De resultaten laten ook zien dat naarmate het aantal waterstofmoleculen toeneemt, het PDOS-overlapgebied tussen de waterstofmoleculen en de twee WS2 moleculen neemt toe.
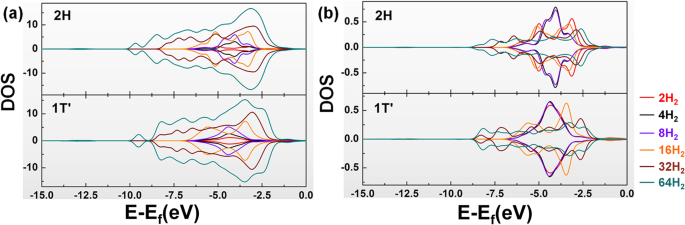
PDOS-resultaten van meerdere H2 adsorptiesystemen voor a alle en b enkele waterstofmoleculen op 2H-WS2 en 1T'-WS2
De interactie tussen waterstofmoleculen en WS2 wordt sterker. Dat onthult de reden voor de toename van de gemiddelde adsorptie-energie wanneer het aantal geadsorbeerde waterstofmoleculen groter wordt.
Om de interactie tussen waterstofmoleculen en de materialen verder te onderzoeken, werd ook het elektronendichtheidsverschil (EDD) onderzoek uitgevoerd. Zoals weergegeven in figuur 5 (planvormen in figuur S5), resulteert de EDD wanneer 4, 16, 32 en 64 waterstofmoleculen worden geadsorbeerd op 2H of 1T′-WS2 werden gepresenteerd. De oranje gebieden vertegenwoordigen positieve waardegebieden, wat wijst op een neiging om elektronen te verkrijgen. Terwijl de blauwe gebieden negatieve gebieden betekenen, die een uitputting van elektronen vertegenwoordigen. Voor zowel 2H als 1T′-WS2 , hadden de oranje gebieden meer kans om in de buurt van S-atomen te verschijnen, terwijl de blauwe gebieden zich in de buurt van H-atomen bevonden. De neiging wordt duidelijker wanneer 32 of 64 waterstofatomen werden geadsorbeerd, zoals figuur 5c, d, g en h laat zien. Er kon ook worden waargenomen dat er oranje en blauwe gebieden waren tussen de waterstofmoleculen wanneer er meer waterstofmoleculen werden geadsorbeerd, wat wijst op interactie tussen de geadsorbeerde H2 moleculen bestaat. Dat draagt bij aan de adsorberende kracht voor elk waterstofmolecuul op het materiaal, waardoor de gemiddelde adsorptie-energie toeneemt. Bovendien is er nog iets dat niet kan worden genegeerd:duidelijke blauwe gebieden kunnen worden gezien wanneer meer waterstofmoleculen worden geadsorbeerd op 1T′-WS2 (Fig. 5 g, h). Terwijl in 2H-gevallen een dergelijk fenomeen niet duidelijk is. Dat toont aan dat de W-atomen ook een proces van elektronenherverdeling hebben doorgemaakt. En de W-atomen in 1T′-WS2 hadden de neiging om meer elektronen aan te bieden om de elektronentoevoer te delen die voornamelijk wordt geleverd door de waterstofmoleculen dan die in 2H-WS2 gevallen. Op basis hiervan werd de werkende kracht op elk waterstofmolecuul enigszins verzwakt. Dat zou de reden kunnen zijn waarom de 1T′-WS2 zou meer waterstofmoleculen kunnen bevatten dan de 2H-WS2 onder de garantie van de gemiddelde adsorberende kracht om matig te zijn.
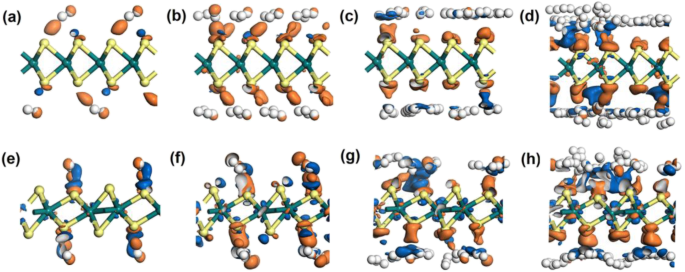
Elektronische verschildichtheid van a 4H2 op 2H-WS2 , b 16U2 op 2H-WS2 , c 32H2 op 2H-WS2 , d 64H2 op 2H-WS2 , e 4H2 op 1T′-WS2 , v 16U2 op 1T′-WS2 , g 32H2 op 1T′-WS2 , en h 64H2 op 1T′-WS2 . De iso-oppervlaktewaarde wordt genomen als 0,002 e/Å
Conclusie
In dit artikel worden waterstofadsorptiemodellen van 2H, 1T en 1T′ monolaag WS2 werden gebouwd. Hun adsorptiecapaciteit aan waterstof wordt onderzocht door middel van lokale dichtheidsbenadering (LDA). Vervolgens, door de adsorptie-energie te vergelijken wanneer meerdere waterstofmoleculen werden geadsorbeerd, werd gevonden dat 1T′-WS2 kan meer waterstofmoleculen bevatten dan 2H-WS2 terwijl de gemiddelde adsorptie-energie in het gematigde bereik ligt (− 0,2 tot -0,6 eV). Het kan de redelijke waterstofadsorptieverhouding tot 2,7 wt% bereiken, meer dan die van 2H-WS2 , wat 2,4 wt% is, wat aangeeft dat de invloed van fase duidelijk is voor waterstofopslag, en 1T′-fase WS2 bezit een grotere waterstofcapaciteit dan de 2H-tegenhanger. Gezien alle resultaten die in deze studie zijn berekend, is 1T′ fase WS2 is een geschikt materiaal voor waterstofadsorptietoepassingen. Het zou een theoretische referentie kunnen zijn voor studies over sterk geïntegreerde waterstofopslagmaterialen.
Beschikbaarheid van gegevens en materialen
Alle gegevens zijn onbeperkt beschikbaar.
Nanomaterialen
- Titanium-ijzer waterstof opslag legering
- Cervoz:case study van industriële flitsmodule
- casestudy over betrouwbaarheid van farmaceutische planten
- Casestudy:aandrijvingen en retrofits op papiersnij-opwinder
- CASE STUDY:De Honda-manier
- Betrouwbaarheidscasestudy bij aluminiumfabriek
- 3 sleutels voor verbeterde plantprestaties
- Apparatuur repareren of vervangen:Casestudy
- Casestudy:Machine Down Crisis-oplossing
- Casestudy:Castrol Syntilo 9913 – Automobiel
- Een casestudy over precisieafsnijding versus stempelen



