Regelbare optische bistabiliteit en vier-golf-menging in een fotonisch-molecuul-optomechanica

Abstract

We onderzoeken theoretisch de niet-lineaire optische fenomenen, waaronder optische bistabiliteit en vier-golfmenging (FWM) -proces in een optomechanisch systeem met samengestelde fotonische molecuulholtes. De fotonische molecuulholte bestond uit twee WGM-microholtes (fluistergalerijmodus), waarbij één WGM-holte een optomechanische holte is met een hoge holtedissipatie κ en de andere WGM-holte is een gewone optische holte met een hoogwaardige factor (Q). Regelen van de parameters van het systeem, zoals de koppelingssterkte J tussen de twee holtes, de verhouding van de vervalsnelheid δ van de twee holtes, en het pompvermogen P , kan de optische bistabiliteit worden gecontroleerd. Verder wordt het FWM-proces dat de normale modussplitsing presenteert ook onderzocht in het FWM-spectrum onder verschillende parameterregimes. Onze studie kan een verder inzicht verschaffen in niet-lineaire verschijnselen in de optomechanische systemen van samengestelde fotonische moleculen.

Achtergrond

Optomechanische systemen (OMS) [1], bestaande uit optische holtes gekoppeld aan mechanische resonatoren en het onderzoeken van door stralingsdruk geïnduceerde coherente foton-fonon-interacties, hebben onlangs veel aandacht getrokken omdat ze een platform bieden om mechanische resonatoren en elektromagnetische velden te manipuleren, en de manier voor mogelijke toepassingen van optomechanische apparaten, zoals fonon laser [2, 3], sensing [4], fonon knijpen [5], de realisatie van samengedrukt licht [6-8], grondtoestand koeling [9-11], en optomechanisch geïnduceerde transparantie (OMIT) [12-15]-geïnduceerd winkellicht in solid-state apparaten [16, 17]. Hoewel de meeste aandacht is besteed aan de enkele OMS, om samengestelde OMS te realiseren door meer optische of mechanische modi te integreren, zoals een mechanische modus gekoppeld aan twee optische modi via stralingsdruk [18, 19] en de fononische interactie tussen twee mechanische resonatoren [20] , 21] uitgegroeid tot een tendens om het OMS en hun potentiële toepassingen in de verwerking van kwantuminformatie verder te onderzoeken. Op basis van de hybride verbinding OMS is de overdracht van een kwantumtoestand [22], OMIT-achtige fononkoeling [23], optomechanische donkere modus [24] en fonon-gemedieerde elektromagnetisch geïnduceerde absorptie [25] uitgebreid onderzocht. In de talrijke samengestelde OMS, als een natuurlijke uitbreiding van de generieke OMS, hebben twee direct gekoppelde WGM-microholtes (Fluistering Gallery Mode) genaamd fotonische moleculen [26, 27] met optomechanisch effect in één WGM-microholte veel aandacht getrokken. Er zijn twee soorten interactie in het samengestelde fotonische-molecuul optomechanische systeem:de eerste is de optomechanische interactie die wordt geïnduceerd door de stralingsdruk en de andere is de holte-holtekoppeling via afstembare fotontunneling. De twee interacties samen leiden tot verschillende interessante fenomenen, waaronder fonon-lasing [2, 3], chaos [28], koeling in de grondtoestand [23] en coherente controle van lichttransmissie [25, 29, 30].

Aan de andere kant biedt OMS ook een platform om het niet-lineaire effect van licht-materie-interactie te onderzoeken. Van alle niet-lineaire fenomenen in OMS, zijn optische bistabiliteit en viergolfmenging (FWM) typische niet-lineaire optische fenomenen die zich richten op de interesse van onderzoekers. In het afgelopen jaar is het bistabiele gedrag van het gemiddelde aantal fotonen in de holte uitgebreid bestudeerd in verschillende OMS, zoals Bose-Einstein condensaatholte optomechanisch systeem [31, 32], OMS met een kwantumbron [33], ultrakoude atomen [34, 35] en andere hybride OMS [36, 37]. Bovendien kan FWM worden beschreven als de holte die wordt aangedreven door een krachtige pomplaser met frequentie ω _p en een zwakke sondelaserfrequentie ω _s , en dan zouden twee pompfotonen zich mengen met een sondefoton via de mechanische modus om een inactief foton op te leveren met frequentie 2ω _p −ω _s in OMS, en het is ook onderzocht in eerdere werken, zoals de modussplitsing in een optomechanisch systeem met sterke koppeling [38], coherent mechanisch aansturende OMS [39, 40] en een optomechanisch systeem met twee modi [41]. Optische bistabiliteit en FWM zijn echter zelden bestudeerd in OMS van samengesteld fotonisch molecuul, waarbij de koppelingssterkte wordt weergegeven door J van de twee holtes spelen een sleutelrol bij het beïnvloeden van deze niet-lineaire optische fenomenen.

In het huidige werk beschouwen we een optomechanisch systeem met samengestelde fotonische molecuulholtes, bestaande uit twee WGM-microholten, waarbij één WGM-holte een optomechanische holte is met dissipatie van hoge holtes κ , en de andere WGM-holte is een gewone optische holte met een hoogwaardige factor (Q) [42]. Zoals Liu et al. [43] aangetoond, blijft het moeilijk om tegelijkertijd een hoge Q-factor en een klein modusvolume (V) te bereiken voor hetzelfde type resonator. In de optomechanica van het fotonische molecuul, door de oorspronkelijk optomechanische holte c te koppelen met dissipatie met hoge caviteit κ (zonder hoge Q) naar een hulpholtemodus a met hoge Q maar grote V, kan de vereiste voor hoge Q en kleine V voor dezelfde holte worden verwijderd. We introduceren een verhoudingsparameter δ =κ _c /κ _een , waar κ _c =ω _c /Q _c en κ _een =ω _een /Q _een zijn de vervalsnelheden van holtemodi c en een (ω _c en ω _een zijn de frequenties van holte c en een ) om het niet-lineaire effect in de optomechanica van fotonische moleculen te onderzoeken. Hier, de optomechanische holte c wordt aangedreven door de pomplaser terwijl de hulpholte a wordt aangedreven door de sondelaser. De holte c is gekoppeld aan holte a via verdwijnend veld, en de koppelingssterkte J tussen de twee holtes kan worden geregeld door de scheiding tussen de twee WGM-holten te variëren [26]. We onderzoeken de optische bistabiliteit en FWM op basis van het samengestelde fotonische molecuul OMS door de koppelingssterkte te variëren J tussen de holteresonatoren, en een afstembare en regelbare optische bistabiliteit en FWM kan worden bereikt door de koppelingssterkte J te manipuleren tussen de twee holtes. Verder, met het aanpassen van de parameter δ en het pompvermogen P , het FWM-proces kan worden gecontroleerd.

Model en theorie

De optomechanica van het fotonische molecuul wordt getoond in Fig. 1. De eerste holte ondersteunt een optische modus c met de frequentie ω _c aangedreven door de pomplaser met frequentie ω _p en de amplitude $\varepsilon _{p}=\sqrt {P/\hbar \omega _{p}}$. De stralingsdruk induceert een mechanische modus b met de mechanische resonatorfrequentie ω _m , en de optomechanische koppelingssnelheid van één foton is g =g ₀ x ₀ (g ₀ =ω _c /R en R is de straal van holte c ), en de nulpuntfluctuatie van de positie van de mechanische oscillator is $x_{0}=\sqrt {\hbar /2M\omega _{m}} $ [13]. Dan, de Hamiltoniaan van de optomechanica c is [13]

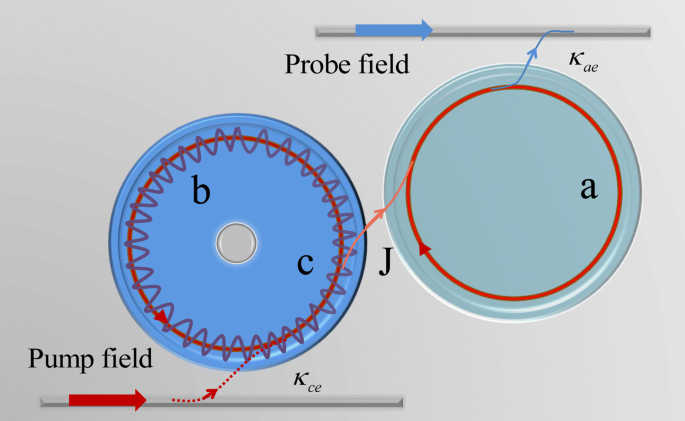
Schematisch diagram van het optomechanische systeem van de samengestelde fotonische molecuulholte, inclusief twee WGM-holten. De eerste WGM-caviteit met hoge caviteitsdissipatie κ is optomechanische holte c aangedreven door een pomplaser, en stralingsdrukkracht induceert de mechanische modus b koppeling aan holte c met koppelsterkte g . De tweede WGM-holte a is een hulpholte aangedreven door een sondelaser met een hoge kwaliteitsfactor (Q). De optomechanische holte c is gekoppeld aan holte a via evanescent field, en we introduceren een parameter J om de koppelingssterkte van de twee holtes te beschrijven, die kan worden gecontroleerd door de scheiding ertussen te variëren [26]

$$ H_{c}=\hbar \Delta_{c}c^{\dag }c+\hbar \omega_{m}b^{\dag }b-\hbar ga^{\dag }a\left(b^ {\dag }+b\right)+i\hbar \sqrt{\kappa_{ce}}\varepsilon_{p}\left(c^{\dag }-c\right), $$ (1)

waar Δ _c =ω _c −ω _p is de ontstemming van het pompveld en de holte c . c en c ^† vertegenwoordigen de bosonische annihilatie- en creatie-operators van de holtemodus c , en b ^† (b ) is de creatie (vernietiging) operator van de mechanische modus. De hulpholte ondersteunt alleen een optische modus a aangedreven door de sondelaser met frequentie ω _s , en zijn amplitude ε _s is $\varepsilon _{s}=\sqrt { P_{s}/\hbar \omega _{s}}$. We introduceren de annihilatie- en creatie-operators a en een ^† om de holte a te beschrijven , en zijn Hamiltoniaan is [13]

$$ H_{a}=\hbar \Delta_{a}a^{\dag }a+i\hbar \sqrt{\kappa_{ae}}\varepsilon_{s}\left(a^{\dag }e^ {-i\Omega t}-ae^{i\Omega t}\right) $$ (2)

waar Δ _een =ω _een −ω _p is de ontstemming van het pompveld en de holte a , en Ω =ω _s −ω _p is de pompsonde-ontstemming. We gebruiken twee taps toelopende vezels om de holtemodus a . te exciteren en holtemodus c als de optische golfgeleider met de koppelingssnelheid κ _ee en κ _ce . De optomechanische holte c koppels naar holte a door een verdwijnend veld, en de holte-holte koppelingssnelheid J kan efficiënt worden afgestemd door de afstand ertussen te veranderen [26]. Wanneer de koppelingssterkte J zwak is tussen de twee holtes, dan is de energie van holte c kan niet gemakkelijk worden overgebracht naar holte a . Omgekeerd, als de koppelingssterkte J neemt toe naarmate de afstand tussen de twee holtes kleiner wordt, dan kan de energie gemakkelijk uit de twee holtes stromen. De lineair gekoppelde interactie tussen de twee holtes wordt beschreven door [26] $\hbar J\left (a^{\dag }c+ac^{\dag }\right)$. Dan is de totale Hamiltoniaan in het roterende golfframe van pompfrequentie ω _c kan worden geschreven [3, 13, 23]

$$ \begin{aligned} H =&\hbar \Delta_{a}a^{\dag }a+\hbar \Delta_{c}c^{\dag }c+\hbar \omega_{m}b^{\dag }b+\hbar J\left(a^{\dag }c+ac^{\dag }\right)-\hbar ga^{\dag }a\left(b^{\dag }+b\right) \ \ &+i\hbar \sqrt{\kappa_{ce}}\varepsilon_{p}\left(c^{\dag }-c\right)+i\hbar \sqrt{ \kappa_{ae}}\varepsilon_{ s}\left(a^{\dag }e^{-i\Omega t}-ae^{i\Omega t}\right). \end{uitgelijnd} $$ (3)

De vervalsnelheid van de modus met twee holtes κ =κ _c =κ _een =κ _ex +κ ₀ met de intrinsieke fotonverliessnelheid κ ₀ , en κ _ex beschrijft de snelheid waarmee energie de optische holte verlaat in zich voortplantende velden [13]. Hier beschouwen we voor de eenvoud alleen de toestand van κ _ex =κ ₀ =κ _ee =κ _ce , en we beschouwen ω _c =ω _een .

We gebruiken de bewegingsvergelijking van Heisenberg $i\hbar \partial _{t}O=[O,H]$ (O =een ,c ,X ) en introduceren overeenkomstige dempings- en ruisoperatoren, en we verkrijgen de quantum Langevin-vergelijkingen als volgt [44]:

$$ \partial_{t}a=-(i\Delta_{a}+\kappa_{a})a-iJc+\sqrt{\kappa_{ae}} \varepsilon_{s}e^{-i\Omega t} +\sqrt{2\kappa_{a}}a_{\text{in}}, $$ (4) $$ \partial_{t}c=-(i\Delta_{c}+\kappa_{c})c +igcX-iJa+\sqrt{\kappa_{ce}} \varepsilon_{p}+\sqrt{2\kappa_{c}}c_{\text{in}}, $$ (5) $$ \partial_{t} ^{2}X+\gamma_{m}\partial_{t}X+\omega_{m}^{2}X=2g\omega_{m}c^{\dagger }c+\xi, $$ (6)

waar X =b ^† +b is de positie-operator en γ _m is de vervalsnelheid van de resonator. een _in en c _in die de Langevin-geluiden beschrijven, volgen de relaties [45]

$$\begin{array}{@{}rcl@{}} \left\langle a_{\text{in}}(t)a_{\text{in}}^{\dagger }\left(t^{ ^{\prime }}\right)\right\rangle &=&\left\langle c_{\text{in}}(t)c_{\text{in}}^{\dolk }\left(t^{ ^{\prime }}\right)\right\rangle =\delta\left(tt^{^{\prime }}\right), \end{array} $$ (7) $$\begin{array}{ @{}rcl@{}} \left\langle a_{\text{in}}(t)\right\rangle &=&\left\langle c_{\text{in}}(t)\right\rangle =0. \end{array} $$ (8)

De resonatormodus wordt beïnvloed door het stochastische krachtproces met de volgende correlatiefunctie [46]

$$ \left\langle \xi^{\dolk }(t)\xi \left(t^{^{\prime }}\right)\right\rangle \,=\,\frac{ \gamma_{m} }{\omega_{m}}\int\! \frac{d\omega }{2\pi }\omega e^{-i\omega \left(tt^{^{\prime }}\right)}\left[1\,+\,\coth \left (\frac{\hbar \omega }{2\kappa_{B}T}\right)\right], $$ (9)

waar k _B is Boltzmann-constante en T geeft de reservoirtemperatuur aan.

Wanneer de optomechanische holte c wordt aangedreven door een krachtige pomplaser, kan de Heisenberg-operator in twee delen worden verdeeld, d.w.z. de gemiddelde waarde in stabiele toestand O ₀ , en kleine fluctuatie δ O met gemiddelde waarde nul 〈δ O 〉=0. De steady-state waarden bepalen de intracaviteit fotonaantallen (n _een =|een _s |² en n _c =|c _s |² ) bepaald door

$$ n_{c}=\frac{\kappa_{ce}\varepsilon_{p}^{2}\left(\Delta_{a}^{2}+\kappa_{a}^{2}\right) } {\left(\Delta^{^{\prime }2}+\kappa_{c}^{2}\right)\left(\Delta_{a}^{2}+\kappa_{a}^{2} \right)+2J^{2}\left(\kappa_{a}\kappa_{c}-\Delta^{^{\prime }}\Delta_{a}\right)+J^{4}}, $ $ (10) $$ n_{a}=\frac{\kappa_{ce}\varepsilon_{p}^{2}J^{2}}{\left(\Delta^{^{\prime }2}+ \kappa_{c}^{2}\right)\left(\Delta_{a}^{2}+\kappa_{a}^{2}\right)+2J^{2}\left(\kappa_{a }\kappa_{c}-\Delta^{^{\prime }}\Delta_{a}\right)+J^{4}}, $$ (11)

waarbij $\Delta ^{^{\prime }}=\Delta _{c}-2g^{2}n_{c}/\omega _{m}$. Deze vorm van gekoppelde vergelijkingen is kenmerkend voor de optische bistabiliteit. In de volgende sectie zullen we de parameters bespreken, zoals het pompvermogen P , de holte-holte koppelingssterkte J , en de verhoudingsparameter δ die de optische bistabiliteit beïnvloeden. Alleen de lineaire termen van de fluctuatie-operatoren behouden en de ansatz maken [47] 〈δ een 〉=een ₊ e ^{−ik Ω t} +een ₋ e ^{ik Ω t} , δ c 〉=c ₊ e ^{−ik Ω t} +c ₋ e ^{ik Ω t} , δ X 〉=X ₊ e ^{−ik Ω t} +X ₋ e ^{ik Ω t} , dan verkrijgen we

$$ a_{-}=\frac{\Lambda_{1}}{\Lambda_{2}-\Lambda_{3}}, $$ (12)

waarbij $\Lambda _{1}=igc_{s}^{2}\eta ^{\ast }J^{2}\varepsilon _{s}\sqrt { \kappa _{ae}}$, Λ ₂ =(ik Δ _{een 2} +κ _een )(ik Δ ₂ +κ _c )[(ik Δ ₁ −κ _c )(ik Δ _{een 1} −κ _een )−J ² ], $\Lambda _{3}=-g^{2}\eta ^{\ast 2}n_{c}^{2}(i\Delta _{a1}-\kappa _{a})( i\Delta _{a2}+\kappa _{a})$, Δ _{een 1} =Δ _een −Ω , Δ _{een 2} =Δ _een +Ω , $\Delta _{1}=\Delta ^{^{\prime }}-\Omega +g\eta n_{c}$, $\Delta _{2}=\Delta ^{^{\ prime }}+\Omega +g\eta ^{\ast }n_{c}$, en $\eta =2g\omega _{m}/(\omega _{m}^{2}-i\ gamma _{m}\Omega -\Omega ^{2})$. Gebruik makend van de standaard input-output relatie [45] $a_{\text {out}}(t)=a_{\text {in}}(t)-\sqrt {2\kappa _{a}}a(t )$, waarbij a _uit (t ) is de uitvoerveldoperator, en verkrijg de verwachtingswaarde van de uitvoervelden:

$$ {\begin{aligned} a_{\text{out}}(t)&=(\varepsilon_{p}-\sqrt{\kappa_{ae}}a_{s})e^{-i\omega_{ p}t}+(\varepsilon_{s}-\sqrt{\kappa_{ae}}a_{+})e^{-i(\delta +\omega_{p})t}-\sqrt{\kappa_{ ae}}a_{-}e^{-i(\delta -\omega_{p})t} \\ &=(\varepsilon_{p}-\sqrt{\kappa_{ae}}a_{s})e ^{-i\omega_{p}t}+(\varepsilon_{s}-\sqrt{\kappa_{ae}}a_{+})e^{-i\omega_{s}t}-\sqrt{\ kappa_{ae}} a_{-}e^{-i(2\omega_{p}-\omega_{s})t} \end{aligned}} $$ (13)

waar a _uit (t ) is de uitvoerveldoperator. Vergelijking (13) laat zien dat het uitvoerveld uit drie termen bestaat. De eerste term komt overeen met het uitgangsveld op het stuurveld met amplitude ε _p en frequentie ω _p . De tweede term komt overeen met het sondeveld met frequentie ω _s gerelateerd aan het anti-Stokes-veld resulterend in OMIT, dat is onderzocht in verschillende optomechanische systemen [12-15, 48]. De laatste komt overeen met het uitvoerveld met frequentie 2 ω _p −ω _s gerelateerd aan het stookveld dat de FWM weergeeft. In het FWM-proces werken de twee fotonen van het aandrijfveld samen met een enkel foton van het sondeveld, elk met frequenties ω _p en ω _s een nieuw foton geboren met frequentie 2 ω _p −ω _s . De FWM-intensiteit in termen van het sondeveld kan worden gedefinieerd als [49]

$$ \text{FWM}=\left\vert \frac{\sqrt{\kappa_{ae}}a_{-}}{\varepsilon_{s}}\right\vert^{2}\text{,} $ $ (14)

die wordt bepaald door de optomechanische koppelingssterkte g , het pompvermogen P , de holte-holte koppelingssterkte J , en de ratio van de vervalsnelheid δ van de twee holtes.

Numerieke resultaten en discussies

In deze sectie onderzoeken we eerst het bistabiele gedrag van het stationaire fotongetal n _c en n _een van de twee holtes volgens Vgl. (10) en (11). Omdat het te omslachtig is om de analytische uitdrukking van de bistabiliteitsconditie te geven, zullen we hier de numerieke resultaten presenteren. We kiezen de parameters vergelijkbaar met die in Ref. [13, 26] :de parameters van holte c als [13]:g ₀ =12 GHz/nm, γ _m =41 kHz, ω _m =51,8 MHz, κ _c =5 MHz, m =20 ng, λ =750 nm, en Q =1500, en de orde van grootte van het pompvermogen is milliwatt (1 mW =10⁻³ W). Voor holte a , beschouwen we ω _een =ω _c en κ _c =κ _een . De koppelsterkte J tussen de twee holtemodi speelt een sleutelrol en kan het bistabiele gedrag en FWM beïnvloeden. Er is experimenteel gerapporteerd dat de koppelingssterkte J hangt af van de afstand tussen holte c en holte a [26] (ook de koppelingssterkte neemt exponentieel af met toenemende afstand van de twee holten). Hier verwachten we de koppelsterkte $ J\sim \sqrt {\kappa _{c}\kappa _{a}}$.

Vergelijkingen (10) en (11) geven de intracaviteit fotonaantallen van optomechanische holte c en gewone holte a zijn gekoppelde derdegraadsvergelijkingen, die bistabiel gedrag vertonen. We beschouwen eerst de toestand van J =0, d.w.z. slechts een enkele optomechanische holte c , en Fig. 2a geeft het gemiddelde intracaviteitsfotongetal n . weer _c van optomechanische holte c als functie van de caviteit-pomp ontstemming Δ _c =ω _c −ω _p met drie pompkrachten. Wanneer het pompvermogen minder is dan P =0,4 mW (zoals P =0,1 mW), is de curve bijna Lorentzian. Met het verhogen van het vermogen P tot een kritische waarde, de optomechanische holte c vertoont bistabiel gedrag, zoals weergegeven in de curven voor P =0,4 mW naar P =0,8 mW, waarbij de aanvankelijk Lorentziaanse resonantiecurve asymmetrisch wordt. Het gemiddelde intracaviteitsfotongetal n _c heeft drie echte wortels (Vgl. (10)), en de grootste en kleinste wortels zijn stabiel en de middelste is onstabiel, wat wordt weergegeven in een ovaal in figuur 2a. Wanneer we echter kijken naar de optische holte a , d.w.z. J ≠0 zoals J =1.0 κ _een , wordt het bistabiele gedrag op sommige manieren verbroken, zoals weergegeven in figuur 2b. Dat komt omdat wanneer optomechanische holte c gekoppeld aan optische holte a , delen van intracaviteit foton nummer n _c van optomechanische holte c zal gekoppeld in optische holte a , en dus intracaviteit foton nummer n _c zal afnemen en dan resulteren in een vernietigd bistabiel gedrag. Afbeelding 2c toont het gemiddelde aantal fotonen in de holte n _c van optomechanische holte c als functie van de holte-holte koppelingssterkte J met drie pompkrachten. Het is duidelijk dat het gemiddelde intracaviteitsfotongetal n _c hangt af van het pompvermogen P , en het intracaviteitsfotongetal n _c neemt altijd af met de toenemende koppelsterkte J omdat delen van het fotongetal zijn gekoppeld in de optische holte a . Verder is een grotere ontstemming van de holtepomp gunstig om het optische bistabiele gedrag te observeren met toenemend pompvermogen P . Afbeelding 2d geeft het gemiddelde aantal intracaviteitsfotonen weer n _c versus het pompvermogen P met holte a bij rode zijbanden (Δ _een =ω _m ) en blauwe zijbanden (Δ _een =−ω _m ), respectievelijk, en de bistabiliteit presenteert het gedrag van de hysteresislus [50]. Onze resultaten verschillen echter van het eerdere werk van een optomechanisch systeem met twee modi zonder rekening te houden met de holte-holtekoppeling J . Daarom is de koppelingssterkte J speelt een belangrijke rol bij de bistabiliteit.

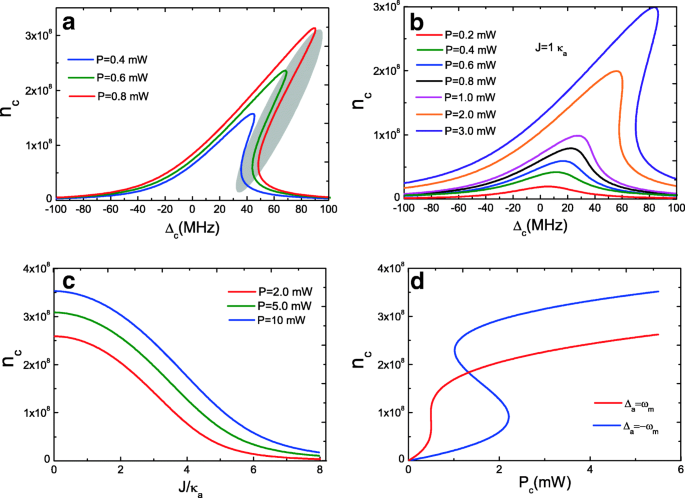
een Gemiddeld aantal intracavity fotons van optomechanische holte c als functie van de caviteit-pomp ontstemming Δ _c met drie pompvermogens bij J =0. b Gemiddeld aantal intracavity fotons van optomechanische holte c als functie van de caviteit-pomp ontstemming Δ _c met verschillende pompvermogens onder J =1.0 κ _een . c Gemiddeld aantal intracaviteit foton n _c van optomechanische holte c als functie van J met drie pompkrachten. d Gemiddeld aantal intracaviteit foton n _c als een functie van P voor Δ _c =Δ _een =ω _m

We onderzoeken verder bistabiel gedrag van optische holte a met vgl. (11). Afbeelding 3a geeft het intracaviteitsfotonnummer n _een van gewone holte a als functie van de caviteit-pomp ontstemming Δ _een =ω _een −ω _p met pompvermogens P =0,1 mW, P =1,0 mW, en P =10 mW bij J =1.0 κ _een . Het is duidelijk dat optische holte a kan zich niet gedragen als bistabiel gedrag vanwege intracaviteit foton nummer n _een van holte a uit holte c kan de bistabiliteit niet handhaven bij een laag pompvermogen. Eigenlijk alleen hoog pompvermogen P kan holte a presenteren bistabiel gedrag, omdat alleen optomechanische holte met hoog pompvermogen c , veel meer fotongetal kan koppelen in optische holte a . We plotten ook het gemiddelde intracaviteitsfotongetal n _een van optische holte a als functie van de koppelsterkte J onder drie pompvermogens zoals weergegeven in Fig. 3b. Het is duidelijk dat wanneer J =0, n _een =0, omdat er geen koppeling is tussen de twee holtes bij J =0, en in deze toestand koppelt geen foton zich in de optische holte a . Met toenemende koppelingssterkte J (verkleining van de afstand van de twee holtes [26]), de intracaviteit fotongetallen n _een van gewone optische holte a toenemen, maar niet altijd. Er is een optimale koppelsterkte J voor de maximale waarde van n _een onder ander pompvermogen, en dan, n _een zal afnemen met de toenemende J . Opmerkelijk is dat de koppelsterkte J tussen de twee holtes kan worden aangepast [26].

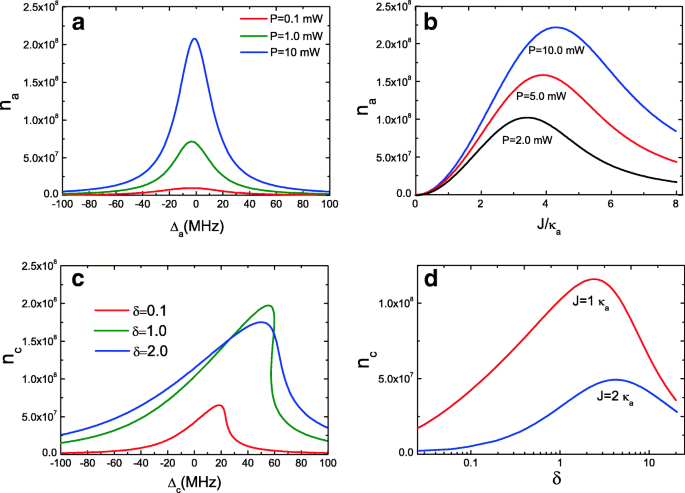
een Gemiddeld aantal intracavity fotons van gewone caviteit a als functie van de caviteit-pomp ontstemming Δ _een met drie pompvermogens bij J =1.0 κ _een . b Gemiddeld aantal intracaviteit foton n _een als functie van J met drie pompkrachten. c Gemiddeld aantal intracaviteit foton n _c als een functie van Δ _c met drie verhoudingsparameters δ . d Gemiddeld aantal intracaviteit foton n _c als een functie van δ voor twee J

Daarnaast beschouwen we een verhoudingsparameter δ =κ _c /κ _een (κ _c =ω _c /Q _c en κ _een =ω _een /Q _een ) om de parameters te onderzoeken van de twee holtes die bistabiel gedrag beïnvloeden. κ is de vervalsnelheid van de holtemodus, die gerelateerd is aan de frequentie en kwaliteitsfactor van de holte. Zoals we weten, is het vanwege de diffractielimiet moeilijk om tegelijkertijd een hoge Q en een kleine V te bereiken voor een holtemodus. Voor een optische holte resulteert een kleinere V die overeenkomt met een grotere stralingsvervalsnelheid in een lagere Q. Hoewel verschillende soorten holtes hun eigen unieke eigenschappen hebben, bestaat het gewicht tussen hoge Q en kleine V nog steeds. Wanneer echter door het koppelen van de oorspronkelijk OMS c met hoge caviteitsdissipatie naar een extra caviteitsmodus a met hoge Q maar grote V, zal het bistabiele gedrag aanzienlijk veranderen. Afbeelding 3c toont het gemiddelde aantal fotonen in de holte n _c van optomechanische holte c als een functie van Δ _een onder verschillende δ =κ _c /κ _een met een ongewijzigde koppelingssterkte J =1.0 κ _een . We kunnen zien dat het bistabiele gedrag kan verschijnen, maar het intracaviteitsfotongetal n _c is klein bij δ =0.1 met J =2 κ _een , d.w.z. κ _c =0.1 κ _een wat betekent Q _c>V _een . Bij het verhogen van de verhouding δ van δ =1,0 tot δ =2.0, het intracaviteitsfotongetal n _c ervaart de verandering van bistabiel gedrag naar bijna Lorentziaans lijnprofiel. Dat wil zeggen wanneer Q _c <Q _een , zal het bistabiele gedrag worden verbroken, maar er is een optimale conditie, d.w.z. Q _c =V _een . In Fig. 3d geven we het intracaviteitsfotonnummer n _c als een functie van δ met twee verschillende J , en uiteraard door de verhoudingsparameter δ . te verhogen , de intracaviteit fotongetallen n _c toenemen. Wanneer het een optimale waarde bereikt voor een gegeven J , dan n _c verminderen. Daarom, het regelen van de holteparameters, zoals de vervalsnelheid κ of de kwaliteitsfactor van de holtes, het bistabiele gedrag kan worden gecontroleerd.

Aan de andere kant, als een typisch niet-lineair optisch fenomeen, onderzoeken we ook het FWM-proces met Vgl. (14) in het optomechanische systeem van fotonische moleculen. Afbeelding 4 geeft het FWM-spectrum weer als een functie van de sondeholte a ontstemming Δ _s =ω _s −ω _een bij Δ _een =Δ _c =0 onder verschillende parameterregimes. Afbeelding 4a–d geeft de evolutie van de FWM-spectra weer onder verschillende pompvermogens P bij J =1.0 κ _een . Het is duidelijk dat de FWM-spectra drie pieken vertonen, waarbij een Lorentz-piek nabij Δ _s =0 en twee modussplitsende pieken bevinden zich op ±ω _m en de FWM-intensiteit neemt af met het verhogen van het pompvermogen. Afbeelding 4e–h toont de verandering van FWM-spectra van J =0.5 κ _een naar J =2.0 κ _een bij pompvermogen P =1,0 mW. Met toenemende koppelingssterkte J van J =0.5 κ _een naar J =2.0 κ _een , veranderen de FWM-spectra aanzienlijk. De verschijnselen kunnen worden verklaard met een beeld van de gekleede toestand die is aangetoond in een optomechanisch systeem met één holte [51].

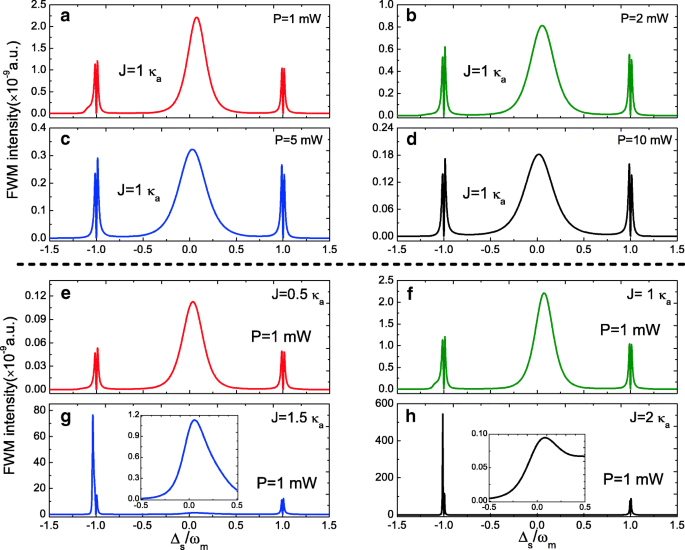
een –d FWM-intensiteit als functie van de genormaliseerde sonde-pomp-ontstemming Δ _s voor ander pompvermogen bij J =1.0 κ _een . e –u FWM-intensiteit als functie van Δ _s voor verschillende J bij pompvermogen P =1,0 mW

Vervolgens onderzoeken we de FWM-spectra bij Δ _een =Δ _c ≠0. Afbeelding 5a–d geeft de FWM-spectra in de rode zijband, d.w.z. Δ _een =Δ _c =ω _m onder een ongewijzigde J =1.0 κ _een met verhoging van het pompvermogen van P =1,0 tot P =10mW. Twee normale modussplitsende pieken verschijnen in de FWM-spectra die zich op ±ω . bevinden _m respectievelijk, en de FWM-intensiteit neemt af met het verhogen van het pompvermogen. Afbeelding 5e–h toont de FWM-spectra in de rode zijband, d.w.z. Δ _een =Δ _c =ω _m onder een vast pompvermogen P =2,0 mW bij toenemende koppelingssterkte J van J =0.5 κ _een naar J =2.0 κ _een . Het is duidelijk dat de FWM-intensiteit toeneemt met toenemende koppelingssterkte J , en de grotere J betekent meer fotongetallen gekoppeld aan optische holte a . Bij het wijzigen van de ontstemming Δ _een en Δ _c van de rode zijband naar de blauwe zijband, d.w.z. Δ _een =Δ _c =−ω _m , verandert de evolutie van de FWM-spectra prominent. Afbeelding 5i–l geeft de FWM-spectra weer op de blauwe zijband onder vier verschillende pompvermogens, en de FWM-intensiteit neemt af naarmate het pompvermogen toeneemt, zelfs bij de blauwe zijband. Behalve twee normale modussplitsende pieken die zich op ±ω . bevinden _m Er verschijnen ook twee scherpe zijbandpieken in de FWM-spectra en hun locatie is gerelateerd aan het pompvermogen. In Fig. 5m–p bespreken we ook de koppelsterkte J die de FWM-spectra onder de blauwe zijband beïnvloeden. Of er andere scherpe zijbandpieken in de FWM-spectra verschijnen, hangt af van de koppelingssterkte J .

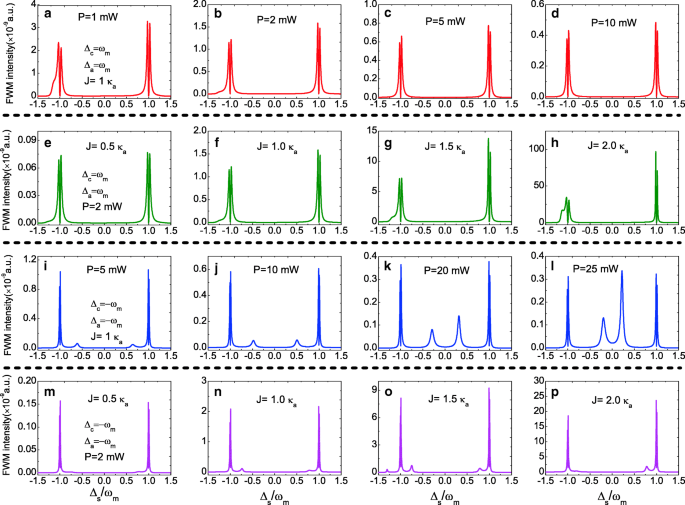
een –d FWM-intensiteit als functie van Δ _s voor verschillend pompvermogen P bij de rode zijband (Δ _c =Δ _een =ω _m ) en J =1.0 κ _een . e –u FWM-intensiteit als functie van Δ _s voor verschillende J onder de rode zijband en de pompkracht P =2,0 mW. ik –ik FWM-intensiteit als functie van Δ _s voor verschillend pompvermogen P bij de blauwe zijband (Δ _c =Δ _een =−ω _m ) en J =1.0 κ _een . m –p FWM-intensiteit als functie van Δ _s voor verschillende J onder de blauwe zijband en de pompkracht P =2,0 mW

Verder, aangezien de verhoudingsparameter δ =κ _c /κ _een kan het aantal intracavitaire fotonen in het samengestelde fotonische molecuul OMS beïnvloeden, de FWM-spectra kunnen worden gemanipuleerd door de parameter δ te regelen . Afbeelding 6a–h geeft de FWM-spectra weer bij ongewijzigde parameters J =2.0 κ _een en P =10 mW onder de rode zijband met toenemende verhouding δ van δ =0.05 tot δ =3.0, en de FWM-intensiteit neemt af met toenemende verhouding δ . While in the blue sideband, other sharp sideband peaks will appear in the FWM spectra as shown in Fig. 6i–p, and the FWM intensity also decreases with increasing the ratio δ . Therefore, with controlling the cavity parameters, like the decay rate κ or the Q of the cavities, the FWM can achieve straightforward in the composite photonic-molecule OMS.

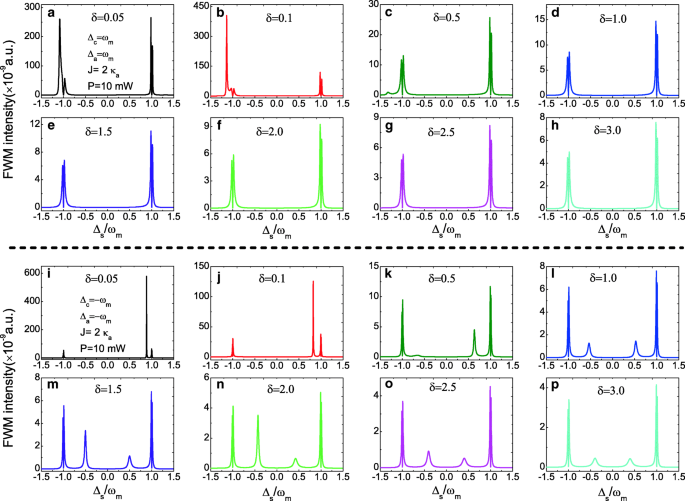
een –u FWM intensity as a function of Δ _s for several different ratio parameters δ at the red sideband (Δ _c =Δ _a =ω _m ) and J =2.0 κ _a , P =10 mW. ik –p FWM intensity as a function of Δ _s for several different ratio parameters δ at the blue sideband (Δ _c =Δ _a =−ω _m ) and J =2.0 κ _a , P =10 mW

Conclusie

We have investigated the optical bistability and four-wave mixing in a composite WGM cavity photonic-molecule optomechanical system, which includes an optomechanical cavity with high-cavity dissipation coupled to an auxiliary cavity with high-quality factor. We investigate the optical bistability under different parameter regimes such as the coupling strength J between the two cavities and the decay rate ratio δ of the two cavities in the system. The optical bistability can be adjusted by the pump field driving the optomechanical cavity, and the intracavity photon number in the two cavities is determined by the coupling strength J . Further, we have also demonstrated how to control the FWM process in the photonic-molecule optomechanical system under different driving conditions (the red sideband and the blue sideband) and different parameter conditions (the coupling strength J and the ratio δ ). Numerical results show that the FWM process can be controlled with such parameters. These results are beneficial for better understanding the nonlinear phenomena in the composite photonic-molecule optomechanical system.

Afkortingen

C-OMS:: Cavity optomechanics systems
FWM:: Four-wave mixing
OMS:: Optomechanics systems
OMIT:: Optomechanically induced transparency
Q:: Quality
V:: Volume
WGM:: Whispering gallery mode

Sterke koppeling tussen een quasi-enkelvoudig molecuul en een plasmonische holte in het vangsysteem Zelfpolarisatie van PVDF-film veroorzaakt door hydrofiele behandeling voor pyro-elektrische sensor met ultralage piëzo-elektrische ruis

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal