Hoge-orde diëlektrische metasurfaces voor zeer efficiënte polarisatiestraalsplitters en optische vortexgeneratoren
Abstract
In dit artikel wordt een diëlektrisch meta-oppervlak van hoge orde op basis van silicium nanobrick-array voorgesteld en onderzocht. Door de lengte en breedte van de nanostenen te regelen, konden de meta-oppervlakken twee verschillende incrementele transmissiefasen leveren voor het X-lineair-gepolariseerde (XLP) en Y-lineair-gepolariseerde (YLP) licht met een extreem hoge efficiëntie van meer dan 88%. Op basis van het ontworpen meta-oppervlak zijn met succes twee polarisatiebundelsplitsers ontworpen die in hoge-orde diffractiemodi werken, wat een hoge doorlaatefficiëntie aantoonde. Daarnaast hebben we ook twee vortexstraalgeneratoren ontworpen die werken in diffractiemodi van hoge orde om vortexstralen te creëren met de topologische ladingen van 2 en 3. Het gebruik van diëlektrische meta-oppervlakken die werken in diffractiemodi van hoge orde zou de weg kunnen effenen voor een verscheidenheid aan nieuwe ultra-efficiënte optische apparaten.
Achtergrond
In de afgelopen jaren is de volledige controle van elektromagnetische golven een opkomend onderzoeksgebied geweest. Om een dergelijke controle te realiseren, hebben metamaterialen veel aandacht getrokken vanwege hun nieuwe fysieke eigenschappen, die kunstmatig als verlangens kunnen worden gemanipuleerd door hun bestanddelen te structureren [1]. Tot nu toe zijn metamaterialen gebruikt om veel uitstekende optische eigenschappen te bereiken, zoals negatieve breking, nulbreking en langzaam licht. Driedimensionaal metamateriaal heeft echter veel nadelen, zoals hoge intrinsieke verliezen en fabricagemoeilijkheden, die de echte toepassingen ervan beperken. Met de ontwikkelingen van nanotechnologie zijn tweedimensionale metamaterialen, of zogenaamde meta-oppervlakken, voorgesteld om deze nadelen te vermijden vanwege hun ultradunne subgolflengtestructuren, relatief eenvoudige fabricage en conforme integraties met systemen [2, 3]. Metasurfaces bestaan typisch uit een reeks optische resonatoren met een subgolflengteperiode en fungeren als interfacediscontinuïteiten. Het zou een abrupte verandering in de amplitude of fase van de invallende bundel kunnen introduceren door de geometrie van de resonator te ontwerpen. Op basis van dit concept zijn verschillende meta-oppervlakken met verschillende functies geïmplementeerd, waaronder afstembare golfgeleider [4, 5], golfplaten [6, 7], lens [8,9,10,11], afwijkende breking [12, 13] , compacte vortexgeneratoren [14,15,16] en hologrammen met hoge resolutie [17,18,19].
Hoewel metasurface een veel betere efficiëntie vertoont in vergelijking met driedimensionale metamaterialen, moet het verlies toch serieus worden overwogen vanwege het algemene gebruik van metaal. Daarom zijn er enkele verbeterde methoden om de transmissie-efficiëntie te verhogen, waaronder de meta-oppervlakken van Huygens en volledig diëlektrische meta-oppervlakken. De meta-oppervlakken van Huygens zouden een lage efficiëntie kunnen vermijden; desalniettemin belemmert de fabricage van de driedimensionale structuren de toepassingen ervan in de realiteit [20]. Gelukkig konden diëlektrische meta-oppervlakken worden geoptimaliseerd om gelijktijdig overlappende elektrische en magnetische resonanties op dezelfde frequenties te hebben en zo volledige 2π mogelijk te maken faseregeling met hoog transmissierendement [21,22,23,24,25,26,27]. De meeste van de gedemonstreerde optische apparaten in de vorige werken gebruiken echter de ±1st bestel diffractiemodi om het golffront van licht te manipuleren in plaats van de hoge-ordemodi [28,29,30]. Onlangs is een nieuwe benadering voorgesteld om het invallende golffront te beheersen en te werken in modi van hoge orde door de discrete fase te moduleren; toch behaalden ze een vrij lage transmissie-efficiëntie vanwege het intrinsieke ohmse verlies van metaal [31, 32].
In dit werk stellen we een diëlektrisch meta-oppervlak voor om het golffront te manipuleren dat werkt in diffractiemodi van hoge orde met een extreem hoge transmissie-efficiëntie. Op basis van het voorgestelde diëlektrische meta-oppervlak zijn twee polariserende bundelsplitsers met abrupte fasediscontinuïteiten ontworpen in de telecommunicatieband en werkend in modi van hoge orde. De polariserende bundelsplitsers zijn in staat om twee verschillende golffronten te genereren voor twee orthogonale ingangspolarisaties met een extreem hoog rendement tot 88%. Daarnaast hebben we ook twee vortexbundelgeneratoren ontworpen met de topologische ladingen van 2 en 3 om het vermogen van het ontworpen meta-oppervlak om licht te manipuleren in diffractiemodi van hoge orde verder aan te tonen.
Methoden
Het schema van de ontworpen diëlektrische meta-oppervlakken wordt getoond in de inzet van figuur 1a. Het is samengesteld uit 900 nm dik kristallijn silicium nanosteen geëtst op een 200 nm dik glazen substraat, waarvan de brekingsindices respectievelijk 3,48 en 1,48 zijn. Door de hoge brekingsindex vertoont silicium hoogwaardige resonantie-eigenschappen en lage intrinsieke ohmse verliezen. Bovendien kan het nanogestructureerde silicium gemakkelijk worden verkregen door volwassen technologie van halfgeleiders met lage fabricagekosten, zoals EBL en FIB. De SiO 2 substraat werd gebruikt waardoor het reflectieverlies en het absorptieverlies bijna verwaarloosd kunnen worden in de golflengte van 1500 nm. De roosterconstante wordt gekozen als S = 650 nm. De geometrische fase van het doorgelaten licht dat wordt geïnduceerd door een silicium nanostaafje hangt dus af van de afmetingen van de nanosteen langs de X- en Y-richtingen. De numerieke simulatie wordt uitgevoerd door de FDTD-methode (finite-different time-domain). In de simulaties werd de perfect op elkaar afgestemde laag (PML) toegevoegd aan de laag boven en onder een cel om te functioneren als absorberende randvoorwaarden. Daarnaast zijn ook de periodieke randvoorwaarden (PBC) toegepast rond een cel of een eenheidscel. De werkingsgolflengte is gekozen op 1500 nm voor de golflengte van optische communicatie.
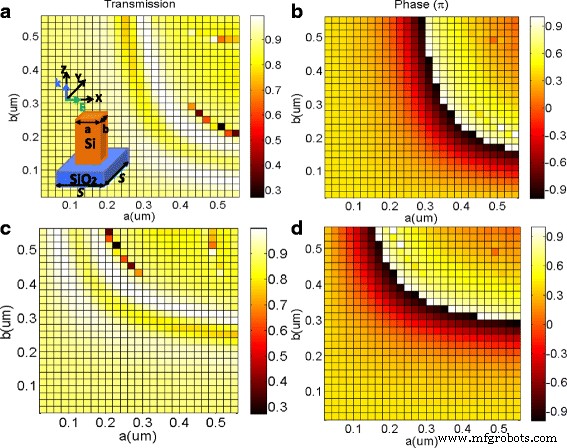
een De transmissie-efficiëntie en b de corresponderende fasevariaties van XLP-licht als functie van parameters a en b . c De co-gepolariseerde transmissie-efficiëntie en d corresponderende fasevariaties van YLP-licht als functie van parameters a en b . De inzet in a toont schematisch de eenheidscel van periodiek diëlektrisch meta-oppervlak bestaande uit een reeks silicium nanostenen bovenop SiO2 substraat. De dikte van silicium nanostenen en SiO2 substraat is ingesteld op respectievelijk 900 nm en 200 nm
Door gebruik te maken van de numerieke simulatie, zoals weergegeven in Fig. 1, worden de co-gepolariseerde uitgezonden efficiëntie en de corresponderende fasevariaties voor zowel X-lineair-gepolariseerd (XLP) licht als Y-lineair-gepolariseerd (YLP) licht berekend als functies van de geometrieën van de siliciumstenen. Wanneer het XLP-licht invalt op het voorgestelde diëlektrische meta-oppervlak, is er een hoge transmissie voor bijna alle nanobaksteendimensies, zoals weergegeven in figuur 1a. Ondertussen impliceert figuur 1b een volledig fasebereik van 0 tot 2π in transmissie van XLP-licht, wat een volledige dekking van de golffrontfase zou kunnen bieden. Wat nog belangrijker is, voor de overgrote meerderheid van de afmetingen hebben de nanostenen meer dan 88% co-gepolariseerde energietransmissie-efficiëntie, wat kan worden toegeschreven aan de lage reflectie en bijna geen absorptie van het diëlektrische meta-oppervlak bij de telecommunicatiegolflengte. De co-gepolariseerde transmissie-efficiëntie en overeenkomstige fasevariaties onder de YLP-incidentie zijn respectievelijk uitgezet in Fig. 1c, d. Vanwege de symmetrie is de afhankelijkheid van optische eigenschappen van het diëlektrische meta-oppervlak van geometrische afmetingen voor YLP-licht vergelijkbaar met die voor XLP-licht, wat duidelijk wordt weergegeven in Fig. 1. Daarom is voor YLP-licht de co-gepolariseerde transmissie-efficiëntie ook hoger dan 88% en het modulerende fasebereik kan variëren van 0 tot 2π .
Kortom, een compleet assortiment faseregeling van 0 tot 2π kan effectief worden bereikt in het geval van XLP- en YLP-incidenten door alleen de geometrische dimensie van nanosteen langs de X-richting te veranderen (d.w.z. a ) en Y-richting (d.w.z. b ), respectievelijk. Bijgevolg zou het bereik van faseregeling kunnen worden uitgebreid tot diffractiemodi van hoge orde (d.w.z. van 0 tot N × 2π ) vanwege de periodiciteit van de fase. Om de veelzijdigheid en nauwkeurige fasecontrole van de ontworpen nanostenen te demonstreren, zijn twee optische apparaten van het transmissietype met een hoog rendement voorgesteld door het meta-oppervlak goed te ontwerpen met een eenvoudige opstelling, inclusief twee polariserende bundelsplitsers en een optische vortexgenerator.
Resultaten en discussie
De polariserende straalsplitsers ontwerpen
On-chip polarisatiecontrole is een belangrijk probleem voor fotonische geïntegreerde schakelingen. De polariserende bundelsplitser is een van de essentiële optische apparaten die worden gebruikt om de polarisatie op een chip te regelen, die kan worden gebruikt om het ingangslicht te scheiden in twee orthogonale polarisatiecomponenten [33, 34]. Volgens de bovenstaande simulatieresultaten kunnen bundelsplitsers met bestuurbare dubbele breking op basis van het voorgestelde diëlektrische meta-oppervlak worden gerealiseerd, wat aangeeft dat twee verschillende fasen van XLP-brekingslicht (φ x ) en YLP-brekingslicht (φ j ) gelijktijdig kunnen worden verkregen door de juiste keuze van de nanosteendiameters a en b , respectievelijk. Daarom ontwerpen we hier meta-oppervlakken en gebruiken deze nieuwe eigenschap om polariserende bundelsplitsers te realiseren om twee orthogonale polarisaties van ingangslicht in twee richtingen te onderscheiden met een hoog doorgelaten rendement tot 88%. Bovendien zou het ontworpen meta-oppervlak niet alleen in de eerste-orde- maar ook in de hogere-orde-diffractiemodi kunnen werken.
We ontwerpen de polariserende bundelsplitsers met 13 diëlektrische nanostenen met drie verschillende permutaties om verschillende ordediffractiemodi met hoge efficiëntie te genereren. In het ontwerp van metasurface 1 (M 1 ), discretiseren we het fasebereik van 0 tot 2π en vanaf 2π naar 0 in 13 nanostenen met gelijke stap van 2π /13 en −2π /13 voor respectievelijk X- en Y-gepolariseerd doorvallend licht. De laterale afmetingen van de 13 geselecteerde silicium nanostenen zijn genummerd in oplopende volgorde, zoals weergegeven in de eerste regel van figuur 2a. Blijkbaar zou het bereik van faseregeling kunnen worden uitgebreid tot diffractiemodus van hoge orde door de eenheidscellen op de juiste manier te selecteren in M 1 en ze te herschikken. Als we bijvoorbeeld de diffractiemodus uitbreiden naar de N-de orde, zou het fasebereik van 0 tot N moeten zijn. × 2π en van N × 2π naar 0 met een faseverschil van N × 2π /13 en −N × 2π /13 tussen twee naburige nanostenen voor respectievelijk X- en Y-gepolariseerd doorgelaten licht. Daarom presenteert de tweede regel van figuur 2a de herschikte supercellen voor de diffractiemodus van de derde orde (M 3 ), waarvan het bereik van faseregeling is van 0 tot 3 × 2π en vanaf 3 × 2π naar 0 met een faseverschil van 3 × 2π /13 en −3 × 2π /13 tussen twee naburige nanostenen voor respectievelijk X- en Y-gepolariseerd doorgelaten licht. Bovendien is het meta-oppervlak (M 5 ) voor de diffractiemodus van de vijfde orde wordt ook geconstrueerd door een set van 13 diëlektrische nanostenen, die ook zijn herschikt om het hele bereik van faseregeling te dekken van 0 tot 5 × 2π en vanaf 5 × 2π naar 0 met een faseverschil van 5 × 2π /13 en −5 × 2π /13 tussen twee naburige nanostenen voor respectievelijk X- en Y-gepolariseerd doorgelaten licht, zoals weergegeven in de derde regel van figuur 2a. Om het idee duidelijk te laten zien, zijn de transmissiefasen van de 13 antennes in drie concrete permutaties onder XLP- en YLP-licht uitgezet in figuur 2b.
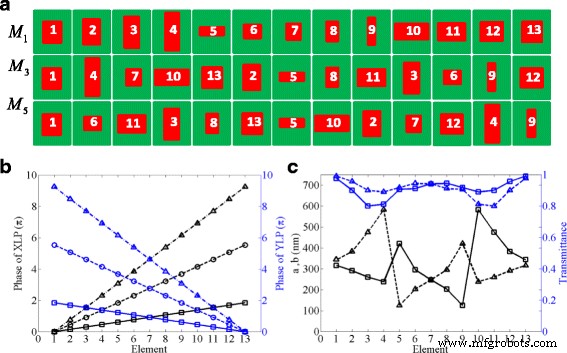
Ontwerp van de diëlektrische meta-oppervlakken met drie verschillende ordediffractiemodi. een Schema's van laterale afmetingen van de 13 ontworpen nanostenen. Eerste regel M 1 :een supercel met uitgezonden fase variërend van 0 tot 2π . Tweede regel M 3 :een herschikte supercel met fase variërend van 0 tot 3 × 2π . Derde regel M 5 :een herschikte supercel met fase variërend van 0 tot 5 × 2π . b De gesimuleerde transmissiefasen van de 13 ontworpen nanostenen van drie verschillende modi onder XLP (zwarte lijnen ) en YLP (blauwe lijnen ) incidenten, respectievelijk. c een (zwarte ononderbroken lijnen ) en b (zwarte stippellijnen ) van de 13 nanostenen die zijn gebruikt in de ontworpen meta-oppervlakken M 1 . De blauwe lijnen vertegenwoordigen de overgedragen efficiëntie van de 13 nanostenen in M 1 onder XLP (ononderbroken lijnen ) en YLP (stippellijnen ) incidenties, respectievelijk
Bovendien zijn de transmissies van de 13 ontworpen nanobricks onder XLP- en YLP-licht gesimuleerd en komen deze goed overeen met de theoretische voorspelling. Fig. 2c toont de geometrische afmetingen van de silicium nanostenen en de doorgelaten efficiëntie van de 13 nanostenen in metasurface M 1 onder XLP en YLP licht. De co-gepolariseerde transmissies van de meeste diëlektrische nanostenen zijn vergelijkbaar en blijven meer dan 88%, hoewel er twee transmissies van nanostenen zijn die bijna 80% behouden. Deze simulatieresultaten bevestigen dat onze ontworpen meta-oppervlakken kunnen worden toegepast om talrijke optische apparaten met hoge efficiëntie te fabriceren.
Numerieke simulaties van polariserende bundelsplitsers worden uitgevoerd door de ontworpen meta-oppervlakken M te verlichten 1 bij normale inval met de gepolariseerde hoek van 45 ° . Het concrete XLP- en YLP-licht kon worden geëxtraheerd uit de hele doorgelaten velden, zoals weergegeven in figuur 3a. Het is duidelijk dat er een goed gedefinieerd golffront bestaat en de co-gepolariseerde uitgezonden efficiëntie van M 1 zijn uitgezet als functies van de uitgezonden hoek in figuur 3b. De piek co-gepolariseerde uitgezonden hoeken zijn −10,2 ° en 10.2 ° voor respectievelijk uitgezonden XLP- en YLP-lichten. De efficiënties van de eerste orde zijn T xx = 85,9% en T jj = 88,4% voor respectievelijk de uitgezonden XLP- en YLP-lichten, waarbij T xx is de gesimuleerde transmissiecoëfficiënt van XLP-licht met de XLP-inval en T jj is de gesimuleerde transmissiecoëfficiënt van YLP-licht met de YLP-inval. Vergeleken met de doorgelaten efficiëntie van de ruimtelijk homogene nanobrick-arrays, is de conversie-efficiëntie enigszins verminderd vanwege de koppeling tussen resonatoren met verschillende afmetingen [35]. Op basis van de algemene wet van Snellius kan de diffractiehoek van invallend licht op een gradiëntmeta-oppervlak worden berekend met θ t = sin −1 [(λ 0 /n t L ) + n ik zonde(θ ik )/n t ], waar n t en n ik zijn de brekingsindexen van de media in respectievelijk de transmissie- en invallende zijde van de interface, θ ik is de invalshoek, λ 0 is de golflengte van licht in vacuüm, en L is de lengte van een supercel [36]. De theoretische resultaten van de eerste orde diffractiehoeken zijn dus ±10,22 ° . Numerieke simulatie en theorie sluiten goed op elkaar aan. Dat wil zeggen dat de ontworpen inrichting kan dienen als polariserende bundelsplitser met een juiste opeenvolgende behandeling. Bovendien is het invallende golffront bijna niet beïnvloed door het gereflecteerde licht van het meta-oppervlak, wat bevestigt dat al het invallende licht met een extreem hoge efficiëntie kan worden doorgelaten vanaf de meta-oppervlakken.
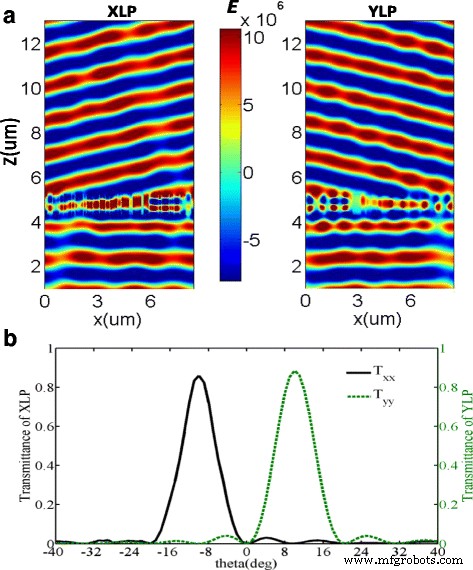
een De elektrische veldverdelingen (E ) van geëxtraheerde verzonden XLP (links ) en YLP (rechts ) licht, wanneer een normaal invallend licht met 45 ° lineaire polarisatie bij de golflengte van 1500 nm uitgezonden door de ontworpen meta-oppervlakken. b De co-gepolariseerde uitgezonden efficiëntie van de ontworpen meta-oppervlakken als de functie van de uitgezonden hoek onder de verlichting van respectievelijk X-gepolariseerde en Y-gepolariseerde lichten
Ter vergelijking:Fig. 4 toont de concrete XLP en YLP uitgezonden elektrische veldverdelingen van de andere twee herschikte diëlektrische meta-oppervlakken gemaakt van nieuw ontworpen supercellen (M 3 en M 5 ) onder de 45 ° lineair gepolariseerd invallend licht. Omdat het uitgezonden fasebereik van de twee supercellen is gewijzigd, zijn de diffractiehoeken van M 3 en M 5 zijn theoretisch berekend op ±32,18 ° en ±62,56 ° , respectievelijk. In Fig. 4a, b bestaan er twee goed gedefinieerde fasefronten met de derde orde diffractiehoeken van −32 ° en 32 ° voor respectievelijk uitgezonden XLP- en YLP-lichten. In figuur 4c, d, is de diffractiehoek van de vijfde orde −63 ° en 63 ° voor respectievelijk uitgezonden XLP- en YLP-lichten. Verder is de gesimuleerde co-gepolariseerde uitgezonden efficiëntie van de ontworpen meta-oppervlakken samengesteld uit herschikte supercel M 3 en M 5 zijn ook geïllustreerd in respectievelijk Fig. 5a, b. De piektransmissiehoeken komen goed overeen met de theoretische diffractiehoeken berekend door de algemene wet van Snell, en de co-gepolariseerde diffractie-efficiënties van de derde orde zijn 82 en 84% voor uitgezonden XLP- en YLP-lichten. De co-gepolariseerde diffractie-efficiëntie van de vijfde orde is echter slechts 73,5 en 78,4% voor uitgezonden XLP- en YLP-licht, wat in wezen wordt veroorzaakt door de ongewenste EM-koppeling tussen naburige nanostenen met verschillende geometrieën. Daarom zouden de ontworpen meta-oppervlakken goed kunnen werken in diffractiemodi van hogere orde door alleen de rangschikking van de 13 diëlektrische nanostenen te wijzigen. Wat nog belangrijker is, is dat is aangetoond dat de diffractiemodus kan worden aangepast door het faseverschil tussen aangrenzende diëlektrische nanostenen in een supercel te regelen.
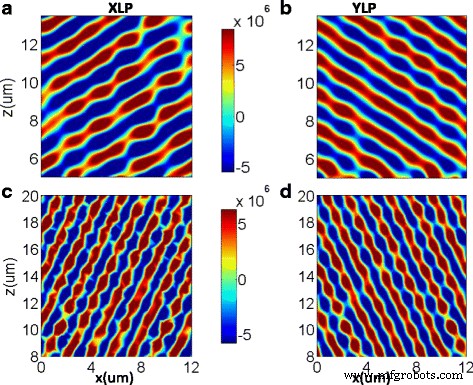
De elektrische veldverdelingen van geëxtraheerde uitgezonden XLP (links ) en YLP (rechts ) onder de normale incidentie van 45 ° lineair polarisatielicht naar de meta-oppervlakken van M 3 (een , b ) en M 5 (c , d ), respectievelijk
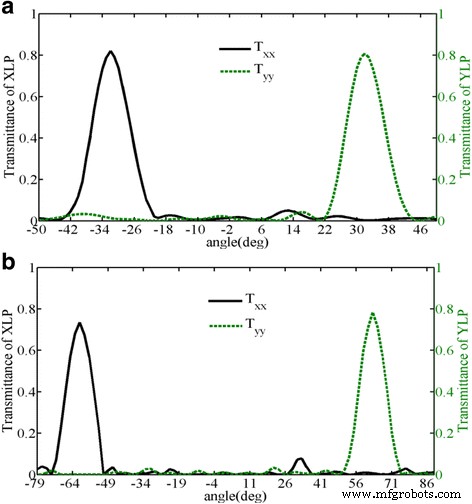
De co-gepolariseerde uitgezonden efficiëntie van de ontworpen meta-oppervlakken bestaande uit herschikte supercel a M 3 en b M 5 als functies van de doorgelaten hoek onder de verlichting van respectievelijk X-gepolariseerd en Y-gepolariseerd licht
Ontwerpen van de optische vortexgeneratoren
De optische vortexbundel heeft een spiraalvormig golffront en draagt een baanimpulsmoment van lℏ [37, 38], waardoor het grote beloften laat zien in lithografie met hoge resolutie [39, 40], optische trapping [41, 42], optische communicatie [43, 44], enzovoort. Hier, de topologische lading l is het aantal wendingen van het golffront en ℏ is de gereduceerde constante van Planck. De vortexbundel met de topologische lading van 1 kan worden gegenereerd door meta-oppervlakken met een spiraalvormig faseprofiel variërend van 0 tot 2π met identieke fasetoename langs de azimutale richting. Om het vermogen van het ontworpen meta-oppervlak om de uitgezonden fase en diffractiemodus te manipuleren verder te demonstreren, ontwerpen we daarom een vortexgenerator die een invallende homogene Gauss-straal kan omzetten in een vortexstraal. Om dit doel te bereiken, rangschikken we de 13 diëlektrische nanostenen van M 1 in de 13 sectoren om een gradiëntfasetoename van 2π . te introduceren /13over de azimutale richting. De uitgezonden intensiteitsprofielen onder XLP-incidentie bij z = 10 μm worden getoond in Fig. 6a en hebben het karakteristieke intensiteitsminimum in het midden dat overeenkomt met een fase-singulariteit. De ruimtelijke fasepatronen met een duidelijke abrupte fasesprong van −π naar π binnen een 2π azimutaal bereik wordt getoond in Fig. 6d, wat aangeeft dat de topologische lading van de optische apparaten in Fig. 6d 1 is.
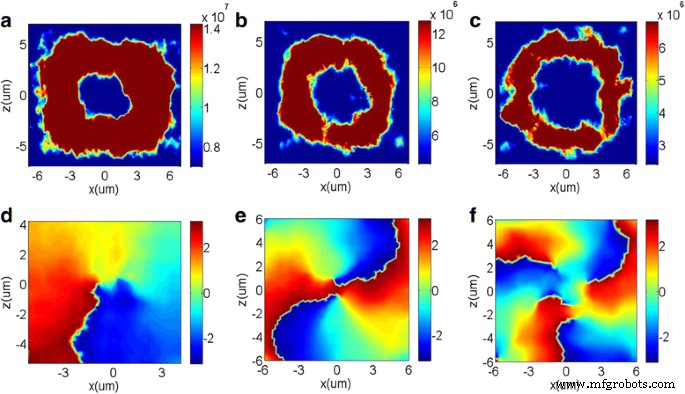
een –c De uitgezonden intensiteitsverdelingen en d –f de fasegolffronten van de gegenereerde vortexbundels bij z = 10μm met topologische lading van l = 1 , 2 , 3 gebaseerd op de meta-oppervlakken M 1 , M 2 , en M 3 onder de X-gepolariseerde incidentie, respectievelijk
Daarnaast ontwerpen we twee andere vortexgeneratoren om vortexbundels te genereren door de opstelling van de nanostenen in M te veranderen. 1 . Deze twee vortexbundelgeneratoren bezitten de topologische ladingen van respectievelijk 2 en 3. Hun uitgezonden intensiteitsprofielen onder XLP-incidentie worden respectievelijk getoond in Fig. 6b, c. De concrete ontwerpbenaderingen moduleren het faseverschil van de nanostenen tot 4π /13 en 6π /13tussen twee aangrenzende diëlektrische nanostenen, gedefinieerd als M 2 en M 3 . Daarom hebben de momentane ruimtelijke faseprofielen in Fig. 6e, f twee en drie duidelijke abrupte fasesprongen van −π naar π , respectievelijk. Het omschakelen van de invallende polarisatie van XLP naar YLP verandert het uitgangsintensiteitspatroon niet, maar de draairichting van het spiraalvormige golffront zal omgekeerd zijn vanwege het afnemende faseverschil tussen de naburige nanostenen. Verder moet worden opgemerkt dat de faseprofielen van hogere orde ook kunnen worden gegenereerd door onze ontworpen diëlektrische meta-oppervlakken.
Conclusies
Concluderend hebben we aangetoond dat meta-oppervlakken met diëlektrische gradiënt bestaan uit een periodieke rangschikking van silicium nanostenen van verschillende grootte, die het ingangslicht zouden kunnen doorlaten met een volledig bereik van manipulatiefase van 0 tot 2π en extreem hoog rendement (meer dan 88%) bij telecommunicatiegolflengte. Gebaseerd op de ontworpen diëlektrische meta-oppervlakken, worden nieuwe polariserende bundelsplitsers die in de hogere orde diffractiemodi werken voorgesteld om twee orthogonale gepolariseerde ingangslichten te scheiden in willekeurige verschillende richtingen. Daarnaast hebben we ook twee vortexbundelgeneratoren ontworpen die werken in de hogere orde diffractiemodi met verschillende topologische ladingen. Ons werk zou ook gemakkelijk kunnen worden uitgebreid tot het ontwerpen van andere optische zendapparatuur met een hoge efficiëntie.
Nanomaterialen
- Proactief onderhoud van hoogspanningsmotoren en generatoren
- Nanovezels en filamenten voor verbeterde medicijnafgifte
- Volledige Terahertz-polarisatiecontrole met verbrede bandbreedte via diëlektrische metasurfaces
- Dip-coating procestechniek en prestatie-optimalisatie voor drie-staten elektrochrome apparaten
- Hoge-orde diëlektrische metasurfaces voor zeer efficiënte polarisatiestraalsplitters en optische vortexgeneratoren
- Silica Aerogel-ondersteunde hydrozinkiet en carbonaat-geïntercaleerd hydrotalciet voor zeer efficiënte verwijdering van Pb(II)-ionen door precipitatietransformatiereacties
- Structurele en zichtbare infrarood optische eigenschappen van Cr-gedoteerde TiO2 voor gekleurde koele pigmenten
- Voorbereiding en optische eigenschappen van GeBi-films met behulp van de moleculaire straal-epitaxiemethode
- Polarisatieconverter met regelbare dubbele breking op basis van hybride volledig diëlektrisch grafeenmetasurface
- PCB-materialen en ontwerp voor hoogspanning
- 500°C-rated optische vezel voor toepassingen bij hoge temperaturen



