Spin-gepolariseerd transport en Spin Seebeck-effect in Triple Quantum Dots met spin-afhankelijke interdot-koppelingen

Abstract

We bestuderen het spinafhankelijke elektronische en thermo-elektrische transport door een structuur die bestaat uit drievoudige kwantumdots (TQD's) gekoppeld aan twee metalen geleiders in de aanwezigheid van spinafhankelijke interdotkoppelingen, wat betrouwbaar is door een statisch magnetisch veld aan te leggen op de tunnelovergangen tussen verschillende stippen. Als de TQD's serieel zijn aangesloten, wordt een 100 % Spin-gepolariseerde conductantie en thermopower ontstaan zelfs voor zeer kleine spin-polarisatie van de interdot koppeling, aangezien de punten zwak aan elkaar zijn gekoppeld. Terwijl als de TQD's ringvormig zijn aangesloten, de Fano-antiresonantie scherpe pieken in de geleiding en het thermovermogen zal veroorzaken. In de aanwezigheid van spin-afhankelijke interdot-koppelingen, zullen de pieken van de spin-up en spin-down thermokrachten verschuiven naar tegengestelde richtingen in het dot-niveauregime, resulterend in grote ofwel 100 % spin-gepolariseerde of pure spin-thermokrachten. Dit laatste ontstaat meestal bij lage temperaturen en is bestand tegen de niveauontstemming, de dot-lead koppeling en de systeemevenwichtstemperatuur.

Inleiding

Samen met de ontwikkeling van spintronica [1-3], heeft spin-caloritronica [4, 5] de afgelopen twee decennia veel aandacht gekregen. In spintronica is een van de meest aantrekkelijke zaken het regelen van de elektronenspin door elektrische vooringenomenheid. Terwijl in spin-caloritronica de spin-controlemethode voornamelijk de thermische bias is, een temperatuurgradiënt die wordt toegepast tussen verschillende uiteinden van het systeem. Het wordt beschouwd als een combinatie van spintronica en thermo-elektriciteit. Van bijzonder belang is het spin Seebeck-effect (SSE) dat pure spinstroom genereert zonder de tegenhanger van de lading, of spin-bias die wordt gekenmerkt door de splitsing van spin-up en spin-down chemische potentialen. Het opent een manier om de overtollige warmte die wordt gegenereerd in nanostructuren te gebruiken om een lager energieverbruik en verbeterde prestaties in thermische apparaten te bereiken. Een dergelijk soort apparaat is ook effectief in het detecteren van de systeemtemperatuurgradiënt met behulp van de vrijheidsgraad van de dragers. Sinds 2008 werden continu enkele grote experimentele doorbraken van de waarneming van SSE gerapporteerd door K. Uchida et.al. in magnetische metalen [6], ferromagnetische isolatoren [7, 8] en ferromagnetische metalen [9]. Het werd vervolgens bestudeerd in ferromagnetische halfgeleiders [10], niet-magnetische materialen met een magnetisch veld [11], paramagnetische materialen [12], antiferromagnetische materialen [13], metaal-ferromagneet isolatorinterface [14], en ook topologische isolatoren [15-17 ].

Het werd bewezen door Mahan en zijn collega dat een delta-achtige vorm van de transmissiefunctie, die gebruikelijk is in laagdimensionale systemen, de efficiëntie van thermo-elektrische apparaten opmerkelijk zal verbeteren [18]. Sindsdien is de nuldimensionale kwantumdot (QD) [19, 20] waarin de dragers in alle drie de dimensies zijn opgesloten uitgebreid bestudeerd om de SSE-coëfficiënt (spin-thermokracht) te verbeteren, die de grootte aangeeft van de gegenereerde spin-bias onder de toestand van een open circuit door de oneindig kleine thermische voorspanning [4-6]. Vooral als er meer dan één transmissiepad in het systeem is, zullen de elektronen met elkaar interfereren en kunnen de interessante Dick [21, 22] of Fano [23, 24] effecten optreden die worden gekenmerkt door een scherpe verandering van de transmissiefunctie en geleiding . Daarom is er veel werk besteed aan het onderzoek naar SSE in verschillende ringvormige of meervoudige padstructuren die QD's bevatten [25-33]. De rijke parameters erin, zoals de afstembare puntniveaus, Coulomb-interactie, magnetische flux, spin-baaninteracties, asymmetrie van de punt-loodkoppelingen maken een effectieve controle van de kwantuminterferentieprocessen mogelijk, wat resulteert in gigantische spin-thermokracht waarvan de grootte kan oplopen tot zo hoog als of zelfs hoger dan die van de lading.

Triple QD's (TQD's) met verschillende vormen zijn opgesteld in experimenten en theoretisch bestudeerd die zich richten op het stabiliteitsdiagram, ladingsrectificatie, ladingsfrustratie, kwantuminterferentie-effect en coherente spincontrole [34–46]. Onder hen zijn de punten die in een ringvorm zijn verbonden interessanter vanwege het bestaan van een kwantuminterferentie-effect [39–46]. In vergelijking met het elektronentransport is het thermo-elektrische effect, met name SSE, zelden bestudeerd in TQD's. In dit artikel onderzoeken we de SSE in TQD's, rekening houdend met spinafhankelijke interdotkoppelingen (zie figuur 1). Door een statisch magnetisch veld aan te leggen op de tunnelovergangen tussen QD's, voert de elektronenspin een Larmor-precessie uit en worden de interdotkoppelingen spinafhankelijk [47, 48]. Onlangs werd ook voorgesteld dat men door gebruik te maken van oscillerende magnetische velden en temporeel gecontroleerde poortspanningen, de elektronengolffuncties van verschillende spincomponenten in verschillende QD's kan scheiden, wat de spin-opgeloste overdrachtssnelheid (koppelingssterkte) induceert [49, 50]. In eerder werk zijn de effecten van spinafhankelijke interdotkoppeling op het genereren van spinstroom al onderzocht [51, 52]. Hier laten we zien dat het de posities van de spin-up en spin-down thermokrachten in tegengestelde richtingen in de ruimte op puntniveau kan verschuiven door de Fano-antiresonantietoestanden te veranderen, wat resulteert in 100 % spin-gepolariseerde of pure spin-thermokrachten waarvan de grootte zo groot kan zijn als die van de lading. Een dergelijk effect is heel anders dan in het geval van spin-onafhankelijke interdot-koppeling [53, 54]. Interessant is dat de verkregen resultaten kunnen worden bereikt met een zeer kleine spin-polarisatie van de interdot-koppelingen.

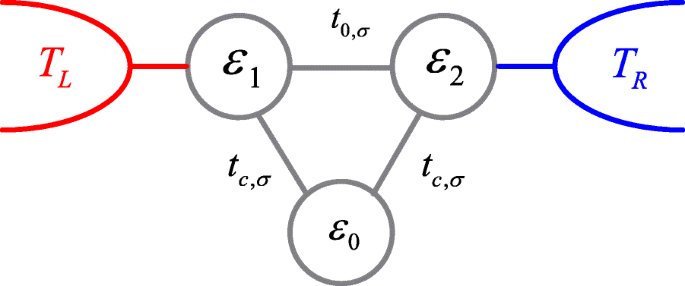
Schematische weergave van het triple quantum dots-systeem. Door een statisch magnetisch veld aan te leggen op de tunnelbarrières tussen de stippen, worden de interdotkoppelingen spinafhankelijk

Model en methoden

De Hamiltoniaan van de TQD's getoond in Fig. 1 verbonden met twee leads kan worden gemodelleerd door de volgende Anderson Hamiltoniaan [25, 33, 51, 52],

$$ \begin{aligned} H=\!\!\sum\limits_{k\beta\sigma}\varepsilon_{k\beta}c_{k\beta\sigma}^{\dag}c_{k\beta\ sigma}\!\,+\,\!\!\sum\limits_{i\sigma}\varepsilon_{i}d_{i\sigma}^{\dag}d_{i\sigma} \!\,+\ ,\!\!\sum\limits_{\sigma}\!(t_{0,\sigma}d_{1\sigma}^{\dag} d_{2\sigma}\!\,+\,t_{c ,\sigma}d_{1\sigma}^{\dag} \!d_{0\sigma}\\ + t_{c,\sigma}d_{0\sigma}^{\dag} d_{2\sigma} \!\,+\,Hc)\,+\,\!\!\sum\limits_{k,\sigma}\left(V_{kL}c_{kL\sigma}^{\dag}d_{1\ sigma}\!\,+\,\!V_{kR}c_{kR\sigma}^{\dag}d_{2\sigma}\!\,+\,\!Hc\right), \end{uitgelijnd } $$ (1)

waarbij $c_{k\beta \sigma }^{\dag } \left (c_{k\beta \sigma }\right)$ met β =L ,R en $d_{i\sigma }^{\dag } \left (d_{i\sigma }\right)$ met i =0,1,2 zijn respectievelijk de creatie (annihilatie) operatoren in lead- β en punt-i met draai σ . We nemen aan dat elke stip een enkel energieniveau bevat ε _ik en negeert de Coulomb-interactie tussen de elektronen in de stippen en de leads. QD-1 en QD-2 zijn aan elkaar gekoppeld door de interdot koppeling t _0,σ =t ₀ (1+σ p ) en naar links en rechts leidt door de dot-lead koppeling V _kL en V _kR , respectievelijk. De QD-0 is verbonden met QD-1 en QD-2 met sterkte t _{c ,σ} =t _c (1+σ p ), waar σ =±1 voor respectievelijk spin-up en spin-down elektronen.

In het lineaire responsregime kunnen we de spinafhankelijke elektrische en warmtestromen afzonderlijk schrijven onder een oneindig klein potentiaalverschil Δ V en een temperatuurverschil Δ T tussen de linker en rechter afleidingen als [25, 33]

$$\begin{array}{*{20}l} &&J_{e,\sigma}=-e^{2}K_{0,\sigma}\Delta V+\frac{e}{T}K_{1, \sigma}\Delta T, \end{array} $$ (2) $$\begin{array}{*{20}l} &&J_{h,\sigma}=eK_{1,\sigma}\Delta V- \frac{1}{T}K_{2,\sigma}\Delta T, \end{array} $$ (3)

waar e is de elektronenlading en T de systeemevenwichtstemperatuur. De coëfficiënten K _{n ,σ} in de bovenstaande vergelijking worden gegeven door [25, 33]

$$\begin{array}{@{}rcl@{}} K_{n,\sigma}=\frac{1}{\hbar}\int (\varepsilon-\mu)^{n}[-\frac {\partial f(\varepsilon,\mu)}{\partial \varepsilon}]T_{\sigma}(\varepsilon)\frac{d\varepsilon}{2\pi}, \end{array} $$ (4 )

waarbij $\hbar $ de gereduceerde constante van Planck is, μ het chemische potentieel van de leads, f (ε ,μ )=1/{1+exp[(ε −μ )/k _B T ]} de Fermi-verdelingsfunctie met Boltzmann-constante k _B .

In verg. (4), de transmissiecoëfficiënt T _σ (ε ) voor elke spincomponent kan worden verkregen in termen van de functie van de vertraagde Groen als [25, 33] $T_{\sigma }(\varepsilon)=\Gamma _{L}\Gamma _{R} \left |G_{ 21,\sigma }^{r}(\varepsilon)\right |^{2}$, waarbij $\Gamma _{L(R)}=2\pi \sum _{k}|V_{kL( R)}|^{2}\delta \left [\varepsilon -\varepsilon _{kL(R)}\right ]$ is de functie voor lijnbreedte. Door de bewegingsvergelijkingsmethode toe te passen, kunnen we gemakkelijk de analytische vorm van $G_{21,\sigma }^{r}(\varepsilon)$ afleiden als [55, 56]

$$ G_{21,\sigma}^{r}(\varepsilon)=\frac{\left(\varepsilon-\varepsilon_{0}\right)t_{0,\sigma}+t_{c,\sigma} ^{2}}{\left(\varepsilon-\varepsilon_{0}\right)\left(\tilde{\varepsilon}_{1}\tilde{\varepsilon}_{2}-t_{0,\sigma }^{2}\right)-t_{c,\sigma}^{2}\left(\tilde{\varepsilon}_{1}+\tilde{\varepsilon}\right)-2t_{0,\sigma }t_{c,\sigma}^{2}}, $$ (5)

waarbij $\tilde {\varepsilon }_{1(2)}=\varepsilon -\varepsilon _{1(2)}+i\Gamma _{L(R)}/2$. De transmissiecoëfficiënt wordt dan verkregen als [55, 56]

$$\begin{array}{@{}rcl@{}} T_{\sigma}(\varepsilon)=\frac{\Gamma_{L}\Gamma_{R}[\left(\varepsilon-\varepsilon_{0 }\right)t_{0,\sigma} +t_{c,\sigma}^{2}]^{2}}{\left|\left(\varepsilon-\varepsilon_{0}\right)\left( \tilde{\varepsilon}_{1}\tilde{\varepsilon}_{2}-t_{0, \sigma}^{2}\right)-t_{c,\sigma}^{2}\left( \tilde{\varepsilon}_{1}+\tilde{\varepsilon}\right)-2t_{0,\sigma}t_{c,\sigma}^{2}\right|^{2}}, \end {array} $$ (6)

De thermokracht (Seebeck-coëfficiënt) van elke spincomponent S _σ wordt berekend onder de voorwaarde van verdwijnende laadstroom J _e =J _{e ,↑} +J _{e ,↓} =0, en wordt gegeven door [25, 33] S _σ =−K _1,σ /(e T K _0,σ ), en de lading (spin) thermopower wordt gegeven door S _{c (s )} =S _↑ +(−)S _↓ .

Resultaten en discussies

In de volgende numerieke berekeningen kiezen we de lijnbreedtefunctie Γ _L =Γ _R =Γ ₀ =1 als de energie-eenheid en fix μ =0 als het energienulpunt. De constanten van e , k _B , en h zijn allemaal ingesteld op 1. Afbeelding 2 toont de spinafhankelijke conductantie G _σ en thermopower S _σ als functies van het puntniveau ε ₀ =ε ₁ =ε ₂ voor t ₀ =0, d.w.z. de TQD's zijn in serie geschakeld. Wanneer de interdotkoppelingen onafhankelijk zijn van spin (p =0), de spin-up en spin-down conductanties in (a) en (b) zijn hetzelfde en ontwikkelen een piek gecentreerd op ε ₀ =0 (zwarte ononderbroken lijnen).

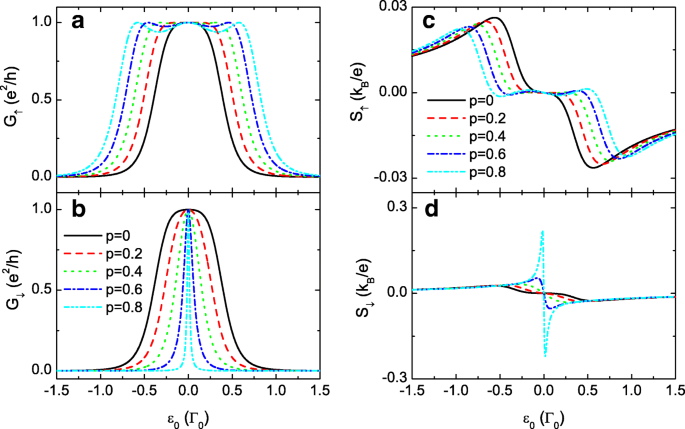
Geleiding en thermokracht voor t ₀ =0. Spin-gepolariseerde geleiding G _σ in een en b , en thermokracht S _σ in c en d als functies van het puntniveau ε ₀ voor vaste t ₀ =0 en verschillende waarden van de spin-polarisatie van de interdot-koppelingen. De andere parameters zijn niveauontstemming Δ =0, temperatuur T =0,001 en t _c =0,3

In aanwezigheid van de spinafhankelijke interdotkoppeling p ≠0, de enkele piek van de spin-up conductantie G _↑ in Fig. 2a evolueert naar een drievoudige piekconfiguratie met ongewijzigde maximale piekwaarde vanwege de verbeterde spin-up interdot-koppeling t _{c ,↑} . Terwijl G _↓ blijft het patroon met één piek met verminderde piekbreedte vanwege de kleinere t _{c ,↓} . Voor t _0,σ =0 en identieke QDs-niveaus (ε ₁ =ε ₂ =ε ₀ ), de transmissiecoëfficiënt in Vgl. (6) reduceert tot

$$\begin{array}{@{}rcl@{}} T_{\sigma}(\varepsilon)=\frac{\Gamma_{0}^{2}t_{c,\sigma}^{4}} {\left\{\left(\varepsilon-\varepsilon_{0}\right)\left[\left(\varepsilon-\varepsilon_{0}\right)^{2}-\Gamma_{0}^{2} /4\right]-2t_{0,\sigma}^{2}\right\}^{2}+\Gamma_{0}^{2}t_{c,\sigma}^{4}}. \end{array} $$ (7)

Er zijn drie resonanties in de transmissiefunctie die zich respectievelijk op ε . bevinden =ε ₀ en $\varepsilon =\varepsilon _{0}\pm \sqrt {2t_{c,\sigma }^{2}+\Gamma _{0}^{2}/4}$. Bij een lage temperatuur ontstaan er drie resonantiepieken in de geleiding bij ε ₀ =μ en $\varepsilon _{0}=\mu \pm \sqrt {2t_{c,\sigma }^{2}+\Gamma _{0}^{2}/4}$, respectievelijk. Voor het geval van zwakke interdot-koppeling, komen de drie pieken samen in een configuratie met één piek, zoals weergegeven door de zwarte lijnen in figuur 2a en. Met toenemende interdot spin-polarisatie p , de waarde van t _{c ,↑} =t _c (1+p ) neemt toe en de drie pieken in de spin-up conductantie worden gescheiden in de energieruimte zoals weergegeven in figuur 2a. Ondertussen is de omvang van t _{c ,↓} wordt kleiner en G _↓ in Fig. 2b blijft dienovereenkomstig een patroon met één piek. Van verg. (6) men kan ook zien dat de piekbreedte wordt verminderd door t . te verkleinen _{c ,↓} .

Wanneer p =0, de thermokrachten van elke spincomponent in figuur 2c en d zijn identiek en antisymmetrisch ten opzichte van het elektron-gat symmetriepunt (ε ₀ =0), wat consistent is met eerdere werken [33, 57]. Vanwege het bestaan van een temperatuurgradiënt die het thermo-elektrische effect genereert, is de temperatuur van de linkerdraad hoger dan die van de rechter, en zijn er meer elektronen boven de chemische potentiaal μ in de linker leiding. Dienovereenkomstig zijn er meer gaten onder μ . Wanneer de energieniveaus van QD's lager zijn dan (boven) μ , de belangrijkste dragers zijn gaten (elektronen) en dan is de thermokracht positief (negatief) [57]. De thermokrachten veranderen hun tekens bij ε ₀ =0 vanwege de compensatie van elektronen en gaten. Met toenemende p , de piekbreedte van de spin-up thermopower S _↑ wordt vergroot met verminderde piekwaarde. Terwijl die van de spin-down is versmald. Interessant is dat de piekwaarde van S _↓ wordt duidelijk verbeterd door p . te verhogen . Voor het geval van grote interdot spinpolarisatie, zoals p =0,8, de piekwaarde van S _↓ is ongeveer tien keer S _↑ met vrijwel onveranderde waarde van de spinafhankelijke conductantie G _σ . Dit kan als volgt worden uitgelegd. Voor positieve p , de interdot-tunnelingsnelheid t _{c ,↑}>t _{c ,↓} en de spin-up elektronen (of gaten) zullen sneller door de QD's gaan dan de spin-down-elektronen. Dienovereenkomstig zijn er meer spin-down-elektronen (gaten) die worden geblokkeerd bij de linker (rechter) leads in vergelijking met de spin-up-elektronen, wat resulteert in een grotere spin-down-spanning als reactie op de temperatuurgradiënt.

Om het verschil tussen S . verder te vergroten _↓ en S _↑ , presenteren we de resultaten van extreem grote p in Fig. 3. We vinden dat de spin-up conductantie G _↑ en thermopower S _↓ worden minder beïnvloed door de variatie van p , die wordt weergegeven door de inzet in Fig. 3a en b ter vergelijking. Met toenemende p , worden de spin-down dragers nog moeilijker te transporteren door de QD's en zullen ze zich ophopen op de leads. Dienovereenkomstig is de waarde van G _↓ wordt monotoon onderdrukt, maar de piekwaarde van S _↓ is opmerkelijk vergroot, wat een effectief middel suggereert voor het genereren van een volledig spin-gepolariseerde thermokracht door de spin-afhankelijke interdot-koppeling. Dit resultaat kan ook veelbelovend zijn bij het detecteren van de temperatuurgradiënt in het systeem door SSE-techniek. Nu zwakke interdotkoppeling de thermokrachtwaarde verbetert, kiezen we voor kleinere t _c met vaste p =0,7 in Fig. 4. In dit geval komen de drie resonantiepieken in zowel de spin-up als spin-down conductanties tot één. De piekbreedte van de conductantie wordt verbreed door t . te vergroten _c wat in overeenstemming is met eerdere resultaten. Fig. 4b en d laten zien dat de grootte van beide S _↑ en S _↓ wordt verbeterd door t . te verkleinen _c . De maxima van de spin-down thermokracht kunnen ook oplopen tot ongeveer 4 k _B /e voor t _c =0.02Γ ₀ . In experimenten zijn de interdot-koppelingen instelbaar door de poortspanning of de dikte van de tunnelbarrière. Daarom is het wellicht beter mogelijk om de thermokracht te verbeteren door t . te veranderen _c met een vaste spin-polarisatie p , aangezien het magnetische veld gewoonlijk moeilijker te controleren is in vergelijking met het elektrische veld. In feite kan grote thermokracht worden verkregen met zeer kleine p onder bepaalde omstandigheden, zoals hieronder weergegeven.

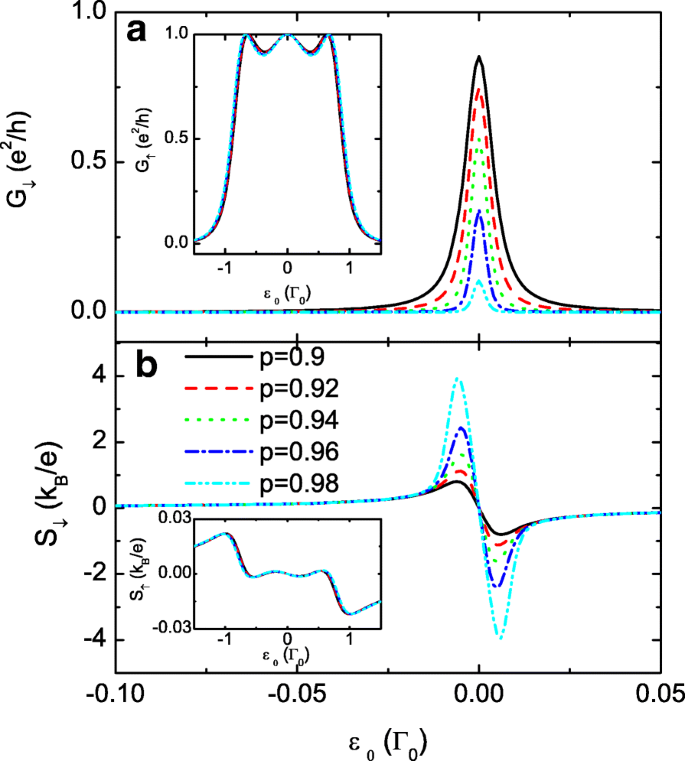
Spin-down conductantie en de thermopower. De spin-down conductantie G _↓ in een en de thermokracht S _↓ in b voor het geval van een grote interdot-koppeling 1>p ≥0.9. De inzet in a is voor G _↑ in een groot puntniveau-regime, en de inzet in b duidt de spin-up thermopower aan in vergelijking met de spin-down. De andere parameters zijn zoals in Afb. 2

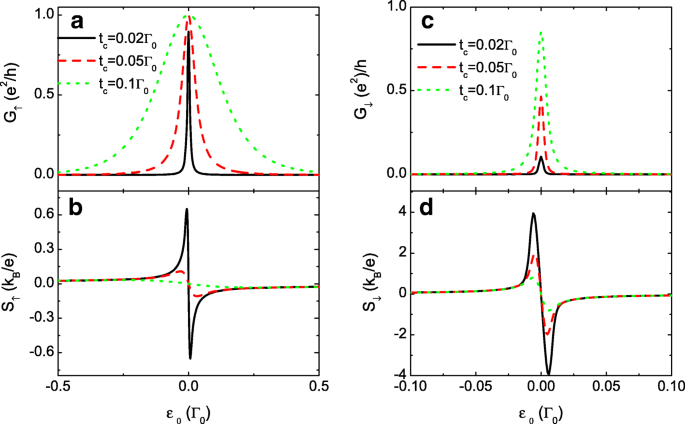
Geleiding en de thermokracht voor verschillende t _c . Spin-gepolariseerde geleiding G _σ in een en c , en de thermokracht S _σ in b en d als functies van het puntniveau ε ₀ voor p =0.7 en verschillende waarden van t _c . De andere parameters zijn zoals in Afb. 2

Als de QD's ringvormig zijn aangesloten, zal het ontstaande Fano-effect de eigenschappen van de conductantie [46] en de thermopower drastisch veranderen. In het bijzonder vindt een gigantische thermopwer plaats rond de Fano-antiresonantietoestand waar de transmissiefunctie de nul nadert T _σ (ε )=0 vanwege de volledige reflectie [25-33]. Vervanging van de elektronenenergie ε door de chemische potentiaal μ in verg. (5), men kan de enige antiresonantietoestand vinden op

$$\begin{array}{@{}rcl@{}} \varepsilon_{0}=\mu+t_{c,\sigma}^{2}/t_{0,\sigma}, \end{array} $$ (8)

die uitsluitend wordt bepaald door de interdot-koppelingen en onafhankelijk van de andere parameters, zoals de puntniveaus ε ₁ , ε ₂ , temperatuur T of de dot-lead hybride matrix Γ _α . Daarom is het vrij eenvoudig om de geleidbaarheid en de thermo-elektrische grootheden in een dergelijk complex systeem aan te passen. Onder de voorwaarde van μ =0, de antiresonantiestatus lokaliseert alleen bij positieve ε ₀ kant. Figuur 5a en b tonen de Fano-antiresonantievallei in de conductantie. De inzet in figuur 5a toont de Fano-lijnvorm van de geleiding in een groot stipniveau-regime. In tegenstelling tot het geval van t ₀ =0 waarin het nulpunt van de thermokracht zich op ε . bevindt ₀ =0, die van t ₀ ≠0 bevindt zich in de antiresonante toestand, waarbij de thermokracht antisymmetrisch is. Voor het geval van p =0, de nulpunten van de thermokrachten van beide spincomponenten liggen op ε ₀ =0,09 zoals weergegeven in Fig. 5c en d. Met toenemende p , ze worden gescheiden en verschoven naar tegenovergestelde richtingen van 0,09. Een brede piek met positieve en negatieve waarden ontstaat respectievelijk aan de twee zijden van de nulpunten. Het is vermeldenswaard dat de waarde van de thermokracht verwaarloosbaar klein is in de andere puntniveau-regimes, die wordt getoond in de inzet van figuur 5c. Het verschuiven van zowel de nulpunten als de pieken in de thermokrachten levert twee interessante resultaten op. Een daarvan is de 100 % spin-gepolariseerde thermokracht wanneer de pieken van S _↑ en S _↓ zijn volledig gescheiden in de energieruimte door vrij grote p waarde. Zie bijvoorbeeld de blauwe stippellijn in Fig. 5c en d voor p =0,4. Aan de rechterkant van ε ₀ =0,09, de waarde van S _↓ nadert tot nul maar S _↑ heeft twee scherpe pieken. Terwijl aan de linkerkant van ε ₀ =0,09, de spin-down thermokracht S _↓ heeft twee pieken met bijna nul S _↑ .

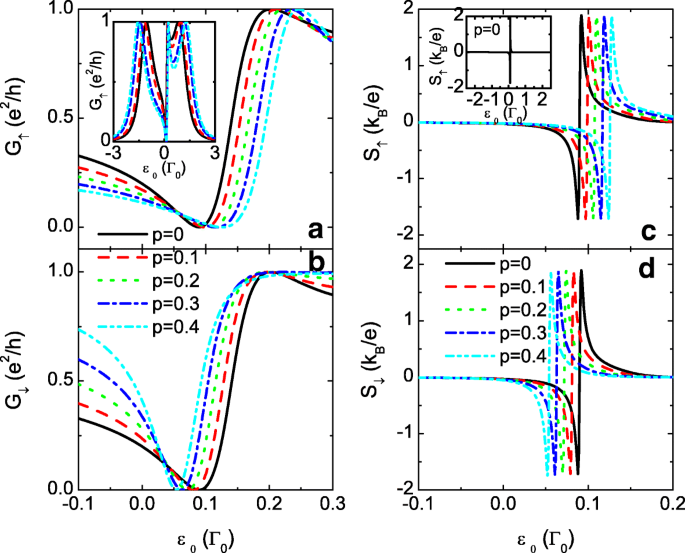
Geleiding en de thermokracht voor t ₀ =1. Spin-gepolariseerde geleiding G _σ in een en b , en de thermokracht S _σ in c en d als functies van het puntniveau ε ₀ voor t ₀ =1, t _c =0.3 en verschillende waarden van de spinpolarisatie van de interdotkoppelingen p . De inzet in a en c zijn respectievelijk de conductantie en de thermopower in een groot dot-niveauregime. De andere parameters zijn zoals in Afb. 2

Het andere interessante resultaat is de pure spin-thermokracht, d.w.z. S _s =S _↑ −S _↓ ≠0 while S _e =S _↑ +S _↓ =0, of pure spinstroom in een gesloten circuit onder eindige thermische voorspanning [58]. Het betekent dat de spin-up en spin-down thermokrachten met gelijke grootte tegengesteld zijn in tekens. De grootte van S _s wordt gemaximaliseerd wanneer de scherpe pieken in de spin-down en spin-up thermokrachten met tegengestelde tekens elkaar ontmoeten op hetzelfde ε ₀ door de spin-polarisatie van de interdot-koppelingen aan te passen p . Zoals weergegeven in Fig. 6a, zijn zowel de nulpunten als de pieken in S _↑ en S _↓ zijn respectievelijk verschoven naar de rechter- en linkerkant van ε ₀ =90k _B T vanwege p ≠0. Als gevolg hiervan ontstaan de negatieve piek in de spin-up thermokracht en de positieve piek in de spin-down één gelijktijdig rond ε ₀ =90k _B T het induceren van de pure spin-thermokracht. Dit gebeurt meestal voor kleine p omdat de twee smalle pieken in S _σ zeer dicht bij de nulpunten liggen, wat wordt bevestigd door de blauwe stippellijn in Fig. 6a met p =0,02. Om duidelijk de kleine energie dominant te laten zien, kiezen we k _B T als de energie-eenheid erin. We benadrukken dat deze pure spin-thermokracht kan worden verkregen met een zeer kleine spin-polarisatie van de interdot-koppeling die kan worden gerealiseerd door een zwak magnetisch veld op de tunnelbarrières aan te leggen. Bovendien is de grootte van de pure spin-thermokracht even groot als de lading (de groene stippellijn).

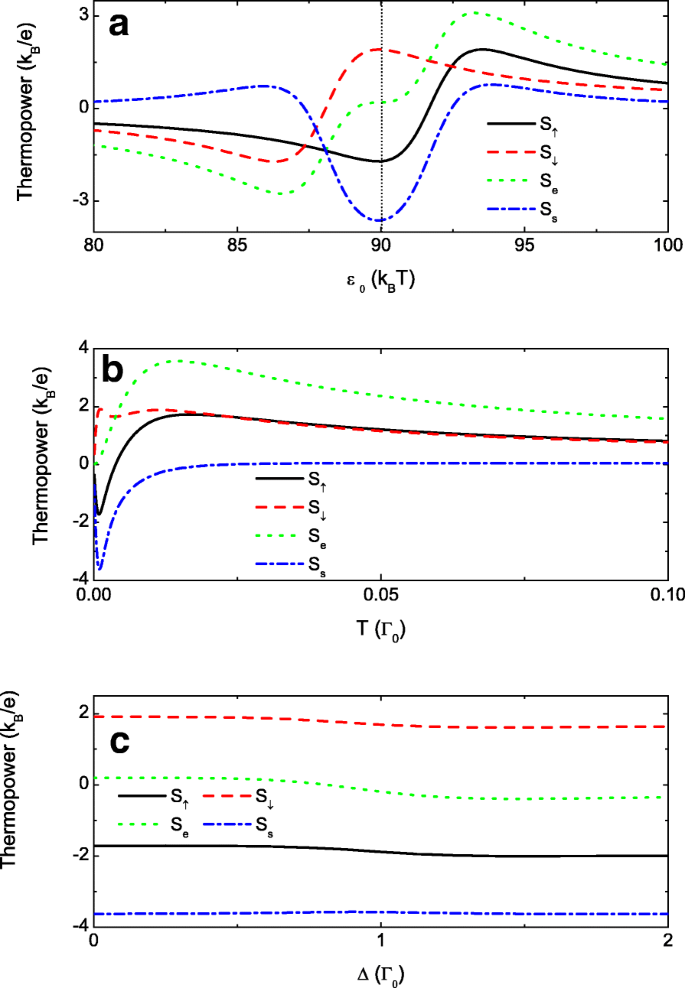
Quantum regelgeving van de thermopowers. De thermokrachten variëren met het puntniveau in a , de temperatuur in b en de niveau-ontstemming in c . Andere parameters zijn p =0.02, t ₀ =1, en t _c =0,3. Het puntniveau in b en c is gekozen als ε ₀ =0.09Γ ₀ . Het niveau ontstemming Δ =0 in een en b , en de temperatuur is T =0,001 in een en c

Ten slotte presenteren we de spin-opgeloste, pure spin en de ladingsthermokrachten die variëren met de temperatuur T en de niveau-ontstemming Δ in respectievelijk Fig. 6b en d. Het puntniveau ε ₀ is gekozen als 0,09 om te focussen op de Fano-antiresonantievallei. Afbeelding 6b laat zien dat bij lage temperatuur S _↑ en S _↓ ontwikkelen pieken met tegengestelde tekens aangegeven door de ononderbroken en onderbroken lijnen, wat resulteert in een vrij grote pure spin-thermokracht S _s (blauwe stippellijn). Nu de lading thermopower S _e kan erg klein zijn, zoals blijkt uit de groene stippellijn. Bij toenemende temperatuur wordt het Fano-effect vernietigd door de willekeurige thermische beweging van de dragers en de pieken in S _σ zijn uitgesmeerd. Als gevolg hiervan is het verschil tussen S _↑ en S _↓ is niet te onderscheiden, en de pure spin-thermokracht nadert tot nul. Figuur 6d laat zien dat de pure spin-thermokracht robuust is tegen het verschil tussen de puntniveaus Δ . Dit komt overeen met het resultaat van vgl. (7) dat de Fano-antiresonantietoestand onafhankelijk is van de punten 1 en 2.

Conclusies

Concluderend hebben we de eigenschappen van de elektrische geleiding en het thermovermogen bestudeerd in TQD's die serieel of circulair zijn verbonden met spin-afhankelijke interdot-koppelingen. Bijzondere aandacht wordt besteed aan het genereren van 100 % spin-gepolariseerde en pure spin-thermokrachten. Het is gebleken dat de eerste kan worden gerealiseerd in de seriële TQD's-configuratie met voldoende grote interdot-koppelingsspinpolarisatie wanneer de stippen vrij sterk met elkaar zijn gekoppeld. Terwijl als de punten zwak gekoppeld zijn, gigantische 100 % spin-gepolariseerde thermopower kan worden gerealiseerd onder zeer kleine interdot-koppeling spinpolarisatie. Wanneer de stippen een cirkelvormige configuratie hebben, is de thermokracht antisymmetrisch ten opzichte van de Fano antiresonantietoestand waarrond de thermokracht scherpe pieken ontwikkelt. Door de spin-polarisatie van de interdot-koppelingen te veranderen, worden de pieken in spin-up en spin-down thermopowers verschoven naar tegengestelde richtingen in het QDs-niveauregime. Nu de 100 % spin-gepolariseerde en pure spin-thermokrachten kunnen op een vrij eenvoudige manier worden gerealiseerd. De huidige resultaten kunnen worden verkregen onder een kleine waarde van de spinpolarisatie van de interdotkoppelingen, wat gunstig is in experimenten.

Covalent gemodificeerd grafeenoxide en polymeer van intrinsieke microporositeit (PIM-1) in gemengde matrix dunne-film composietmembranen Carbon Dots @ Platinum Porphyrin Composite als theranostic nanoagent voor efficiënte fotodynamische kankertherapie

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal