MATLAB - Veeltermen

MATLAB vertegenwoordigt polynomen als rijvectoren die coëfficiënten bevatten die zijn gerangschikt op aflopende machten. Bijvoorbeeld de vergelijking P(x) =x ⁴ + 7x ³ - 5x + 9 kan worden weergegeven als −

p =[1 7 0 -5 9];

Polynomen evalueren

De polyvale functie wordt gebruikt voor het evalueren van een polynoom op een gespecificeerde waarde. Om bijvoorbeeld onze vorige polynoom p . te evalueren , typ bij x =4 −

p = [1 7 0  -5 9];
polyval(p,4)

MATLAB voert de bovenstaande instructies uit en retourneert het volgende resultaat −

ans = 693

MATLAB biedt ook de polyvalm functie voor het evalueren van een matrixpolynoom. Een matrixpolynoom is een polynoom met matrices als variabelen.

Laten we bijvoorbeeld een vierkante matrix X maken en de polynoom p evalueren, bij X −

p = [1 7 0  -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)

MATLAB voert de bovenstaande instructies uit en retourneert het volgende resultaat −

ans =
      2307       -1769        -939        4499
      2314       -2376        -249        4695
      2256       -1892        -549        4310
      4570       -4532       -1062        9269

De wortels van veeltermen vinden

De roots functie berekent de wortels van een polynoom. Om bijvoorbeeld de wortels van onze polynoom p te berekenen, typt u −

p = [1 7 0  -5 9];
r = roots(p)

MATLAB voert de bovenstaande instructies uit en retourneert het volgende resultaat −

r =
   -6.8661 + 0.0000i
   -1.4247 + 0.0000i
   0.6454 + 0.7095i
   0.6454 - 0.7095i

De functie poly is een inverse van de wortelsfunctie en keert terug naar de polynoomcoëfficiënten. Bijvoorbeeld −

p2 = poly(r)

MATLAB voert de bovenstaande instructies uit en retourneert het volgende resultaat −

p2 =

   Columns 1 through 3:

      1.00000 + 0.00000i   7.00000 + 0.00000i   0.00000 + 0.00000i

   Columns 4 and 5:

      -5.00000 - 0.00000i   9.00000 + 0.00000i

Polynomiale curve-aanpassing

De polyfit functie vindt de coëfficiënten van een polynoom die past bij een set gegevens in de kleinste-kwadratenzin. Als x en y twee vectoren zijn die de x- en y-gegevens bevatten die moeten worden aangepast aan een polynoom van n-graden, dan krijgen we de polynoom die bij de gegevens past door −

p = polyfit(x,y,n)

Voorbeeld

Maak een scriptbestand en typ de volgende code −

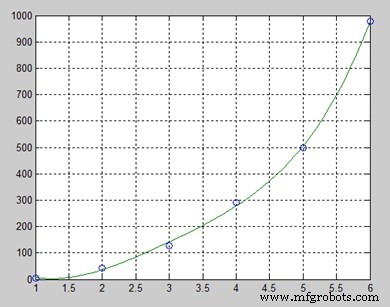
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67];   %data
p = polyfit(x,y,4)   %get the polynomial

% Compute the values of the polyfit estimate over a finer range, 
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;          
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on

Wanneer u het bestand uitvoert, geeft MATLAB het volgende resultaat weer −

p =
   4.1056  -47.9607  222.2598 -362.7453  191.1250

En plot de volgende grafiek −