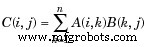MATLAB - Operators
Een operator is een symbool dat de compiler vertelt om specifieke wiskundige of logische manipulaties uit te voeren. MATLAB is ontworpen om voornamelijk op hele matrices en arrays te werken. Daarom werken operators in MATLAB zowel aan scalaire als niet-scalaire gegevens. MATLAB staat de volgende soorten elementaire bewerkingen toe −
- Rekenkundige operatoren
- Relationele operators
- Logische operators
- Bitgewijze bewerkingen
- Bewerkingen instellen
Rekenkundige operatoren
MATLAB staat twee verschillende soorten rekenkundige bewerkingen toe −
- Matrix rekenkundige bewerkingen
- Array rekenkundige bewerkingen
Matrix rekenkundige bewerkingen zijn hetzelfde als gedefinieerd in lineaire algebra. Array-bewerkingen worden element voor element uitgevoerd, zowel op eendimensionale als multidimensionale array.
De matrix-operators en array-operators worden onderscheiden door het punt-symbool (.). Omdat de bewerking voor optellen en aftrekken echter hetzelfde is voor matrices en arrays, is de operator in beide gevallen hetzelfde. De volgende tabel geeft een korte beschrijving van de operators −
Voorbeelden tonen
| Zr.nr. | Operator en beschrijving |
|---|---|
| 1 | + Toevoeging of unaire plus. A+B telt de waarden op die zijn opgeslagen in variabelen A en B. A en B moeten dezelfde grootte hebben, tenzij één een scalair is. Een scalaire waarde kan worden toegevoegd aan een matrix van elke grootte. |
| 2 | - Aftrekken of unaire min. A-B trekt de waarde van B af van A. A en B moeten dezelfde grootte hebben, tenzij één een scalair is. Een scalair kan worden afgetrokken van een matrix van elke grootte. |
| 3 | * Matrix vermenigvuldiging. C =A*B is het lineaire algebraïsche product van de matrices A en B. Meer precies,
Voor niet-scalaire A en B moet het aantal kolommen van A gelijk zijn aan het aantal rijen van B. Een scalair kan een matrix van elke grootte vermenigvuldigen. |
| 4 | .* Matrixvermenigvuldiging. A.*B is het product per element van de arrays A en B. A en B moeten dezelfde grootte hebben, tenzij een van beide een scalair is. |
| 5 | / Slash of matrix juiste verdeling. B/A is ongeveer hetzelfde als B*inv(A). Meer precies, B/A =(A'\B')'. |
| 6 | ./ Array juiste verdeling. A./B is de matrix met elementen A(i,j)/B(i,j). A en B moeten dezelfde grootte hebben, tenzij een van hen een scalair is. |
| 7 | \ Backslash of matrix linker divisie. Als A een vierkante matrix is, is A\B ongeveer hetzelfde als inv(A)*B, behalve dat het op een andere manier wordt berekend. Als A een n-by-n matrix is en B een kolomvector met n componenten, of een matrix met meerdere van dergelijke kolommen, dan is X =A\B de oplossing van de vergelijking AX =B . Er wordt een waarschuwingsbericht weergegeven als A slecht geschaald of bijna enkelvoudig is. |
| 8 | .\ Array linker divisie. A.\B is de matrix met elementen B(i,j)/A(i,j). A en B moeten dezelfde grootte hebben, tenzij een van hen een scalair is. |
| 9 | ^ Matrix-kracht. X^p is X tot de macht p, als p een scalair is. Als p een geheel getal is, wordt de macht berekend door herhaalde kwadratuur. Als het gehele getal negatief is, wordt X eerst geïnverteerd. Voor andere waarden van p worden eigenwaarden en eigenvectoren berekend, zodat als [V,D] =eig(X), dan X^p =V*D.^p/V. |
| 10 | .^ Array macht. A.^B is de matrix met elementen A(i,j) tot de macht B(i,j). A en B moeten dezelfde grootte hebben, tenzij een van hen een scalair is. |
| 11 | ' Matrix transponeren. A' is de lineaire algebraïsche transponering van A. Voor complexe matrices is dit de complexe geconjugeerde transponering. |
| 12 | .' Matrix transponeren. EEN.' is de array-transponering van A. Voor complexe matrices is er geen conjugatie. |
Relationele operators
Relationele operators kunnen ook werken aan zowel scalaire als niet-scalaire gegevens. Relationele operators voor arrays voeren element-voor-element vergelijkingen uit tussen twee arrays en retourneren een logische array van dezelfde grootte, met elementen ingesteld op logische 1 (true) waar de relatie waar is en elementen ingesteld op logisch 0 (false) waar het is niet.
De volgende tabel toont de relationele operatoren die beschikbaar zijn in MATLAB −
Voorbeelden tonen
| Sr.nr. | Operator en beschrijving |
|---|---|
| 1 | < Minder dan |
| 2 | <= Kleiner dan of gelijk aan |
| 3 | > Groter dan |
| 4 | >= Groter dan of gelijk aan |
| 5 | == Gelijk aan |
| 6 | ~= Niet gelijk aan |
Logische operators
MATLAB biedt twee soorten logische operators en functies −
-
Elementsgewijs − Deze operators werken op overeenkomstige elementen van logische arrays.
-
Kortsluiting − Deze operators werken op scalaire en logische uitdrukkingen.
Elementgewijze logische operators werken element voor element op logische arrays. De symbolen &, | en ~ zijn de logische array-operators AND, OR en NOT.
Logische operatoren voor kortsluiting maken kortsluiting mogelijk bij logische bewerkingen. De symbolen &&en || zijn de logische kortsluitoperatoren AND en OR.
Voorbeelden tonen
Bitgewijze bewerkingen
Bitsgewijze operators werken op bits en voeren bit-voor-bit bewerkingen uit. De waarheidstabellen voor &, | en ^ zijn als volgt −
| p | q | p &q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Neem aan dat als A =60; en B =13; Nu in binair formaat zullen ze als volgt zijn −
A =0011 1100
B =0000 1101
-----------------
A&B =0000 1100
A|B =0011 1101
A^B =0011 0001
~A =1100 0011
MATLAB biedt verschillende functies voor bitsgewijze bewerkingen zoals 'bitsgewijze en', 'bitsgewijze of' en 'bitsgewijze niet'-bewerkingen, ploegendienst, enz.
De volgende tabel toont de veelgebruikte bitsgewijze bewerkingen −
Voorbeelden tonen
| Functie | Doel |
|---|---|
| bitand(a, b) | Bitgewijs EN van gehele getallen a en b |
| bitcmp(a) | Bitgewijze aanvulling van a |
| bitget(a,pos) | Bit ophalen op gespecificeerde positie pos , in de integer-array a |
| bitor(a, b) | Bitgewijze OR van gehele getallen a en b |
| bitset(a, pos) | Stel bit in op specifieke locatie pos van een |
| bitshift(a, k) | Retourneert a naar links verschoven met k bits, gelijk aan vermenigvuldigen met 2 k . Negatieve waarden van k komen overeen met het naar rechts verschuiven van bits of delen door 2 |k| en afronding naar het dichtstbijzijnde gehele getal naar negatief oneindig. Eventuele overloopbits worden afgekapt. |
| bitxor(a, b) | Bitgewijze XOR van gehele getallen a en b |
| swapbytes | Byte volgorde omwisselen |
Bewerkingen instellen
MATLAB biedt verschillende functies voor set-operaties, zoals unie, intersectie en testen voor set-lidmaatschap, enz.
De volgende tabel toont enkele veelgebruikte setbewerkingen −
Voorbeelden tonen
| Zr.nr. | Functie en beschrijving |
|---|---|
| 1 | snijden(A,B) Stel de kruising van twee arrays in; geeft de waarden terug die gemeenschappelijk zijn voor zowel A als B. De geretourneerde waarden zijn in gesorteerde volgorde. |
| 2 | kruisen(A,B,'rijen') Behandelt elke rij van A en elke rij van B als afzonderlijke entiteiten en retourneert de rijen die gemeenschappelijk zijn voor zowel A als B. De rijen van de geretourneerde matrix zijn in gesorteerde volgorde. |
| 3 | lid(A,B) Retourneert een array van dezelfde grootte als A, met 1 (true) waarbij de elementen van A in B worden gevonden. Elders wordt 0 (false) geretourneerd. |
| 4 | ismember(A,B,'rijen') Behandelt elke rij van A en elke rij van B als afzonderlijke entiteiten en retourneert een vector die 1 (true) bevat, waarbij de rijen van matrix A ook rijen van B zijn. Elders retourneert het 0 (false). |
| 5 | gesorteerd(A) Retourneert logische 1 (true) als de elementen van A in gesorteerde volgorde staan en anders logische 0 (false). Ingang A kan een vector zijn of een N-by-1 of 1-by-N celarray van strings. A wordt als gesorteerd beschouwd als A en de uitvoer van sort(A) zijn gelijk. |
| 6 | gesorteerd(A, 'rijen') Retourneert logische 1 (true) als de rijen van tweedimensionale matrix A in gesorteerde volgorde staan, en anders logische 0 (false). Matrix A wordt als gesorteerd beschouwd als A en de output van sortrows (A) zijn gelijk. |
| 7 | setdiff(A,B) Stelt het verschil van twee arrays in; retourneert de waarden in A die niet in B zijn. De waarden in de geretourneerde array zijn in gesorteerde volgorde. |
| 8 | setdiff(A,B,'rijen') Behandelt elke rij van A en elke rij van B als afzonderlijke entiteiten en retourneert de rijen van A die niet in B staan. De rijen van de geretourneerde matrix zijn in gesorteerde volgorde. De optie 'rijen' ondersteunt geen celarrays. |
| 9 | setxor Stelt exclusieve OR van twee arrays in |
| 10 | vereniging Stelt vereniging van twee arrays in |
| 11 | uniek Unieke waarden in array |
MATLAB