MATLAB - Integratie
Integratie behandelt twee wezenlijk verschillende soorten problemen.
-
In het eerste type wordt de afgeleide van een functie gegeven en willen we de functie vinden. Daarom keren we in principe het proces van differentiatie om. Dit omgekeerde proces staat bekend als anti-differentiatie, of het vinden van de primitieve functie, of het vinden van een onbepaalde integraal .
-
Het tweede type problemen houdt in dat een zeer groot aantal zeer kleine hoeveelheden wordt opgeteld en vervolgens een limiet wordt genomen als de grootte van de hoeveelheden nul nadert, terwijl het aantal termen tot oneindig neigt. Dit proces leidt tot de definitie van de definitieve integraal .
Bepaalde integralen worden gebruikt voor het vinden van oppervlakte, volume, zwaartepunt, traagheidsmoment, arbeid verricht door een kracht en in tal van andere toepassingen.
Onbepaalde integraal vinden met MATLAB
Als de afgeleide van een functie f(x) f'(x) is, dan zeggen we per definitie dat een onbepaalde integraal van f'(x) met betrekking tot x f(x) is. Bijvoorbeeld, aangezien de afgeleide (met betrekking tot x) van x 2 is 2x, kunnen we zeggen dat een onbepaalde integraal van 2x x 2 . is .
In symbolen −
f'(x 2 ) =2x , daarom,
∫ 2xdx =x 2 .
Onbepaalde integraal is niet uniek, omdat afgeleide van x 2 + c, voor elke waarde van een constante c, is ook 2x.
Dit wordt uitgedrukt in symbolen als −
∫ 2xdx =x 2 + c .
Waarbij c een 'willekeurige constante' wordt genoemd.
MATLAB biedt een int commando voor het berekenen van integraal van een uitdrukking. Om een uitdrukking voor de onbepaalde integraal van een functie af te leiden, schrijven we −
int(f);
Bijvoorbeeld uit ons vorige voorbeeld −
syms x int(2*x)
MATLAB voert de bovenstaande instructie uit en retourneert het volgende resultaat −
ans = x^2
Voorbeeld 1
Laten we in dit voorbeeld de integraal zoeken van enkele veelgebruikte uitdrukkingen. Maak een scriptbestand en typ de volgende code erin −
syms x n int(sym(x^n)) f = 'sin(n*t)' int(sym(f)) syms a t int(a*cos(pi*t)) int(a^x)
Wanneer u het bestand uitvoert, wordt het volgende resultaat weergegeven −
ans = piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)]) f = sin(n*t) ans = -cos(n*t)/n ans = (a*sin(pi*t))/pi ans = a^x/log(a)
Voorbeeld 2
Maak een scriptbestand en typ de volgende code erin −
syms x n int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pretty(int(1 - 10*x + 9 * x^2)) int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2) pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))
Merk op dat de mooie functie retourneert een uitdrukking in een beter leesbaar formaat.
Wanneer u het bestand uitvoert, wordt het volgende resultaat weergegeven −
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2
Definitieve integrale vinden met MATLAB
Per definitie is een bepaalde integraal in feite de limiet van een som. We gebruiken bepaalde integralen om gebieden te vinden zoals het gebied tussen een kromme en de x-as en het gebied tussen twee krommen. Bepaalde integralen kunnen ook in andere situaties worden gebruikt, waar de vereiste hoeveelheid kan worden uitgedrukt als de limiet van een som.
De int functie kan worden gebruikt voor definitieve integratie door de limieten te overschrijden waarover u de integraal wilt berekenen.
Om te berekenen
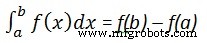
wij schrijven,
int(x, a, b)
Om bijvoorbeeld de waarde van te berekenen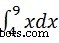 
we schrijven −
int(x, 4, 9)
MATLAB voert de bovenstaande instructie uit en retourneert het volgende resultaat −
ans = 65/2
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));
Octave voert de code uit en geeft het volgende resultaat −
Area: 32.500
Een alternatieve oplossing kan als volgt worden gegeven met de functie quad() die door Octave wordt geleverd −
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));
Octave voert de code uit en geeft het volgende resultaat −
Area: 32.500
Voorbeeld 1
Laten we de oppervlakte berekenen tussen de x-as en de kromme y =x 3 −2x+5 en de ordinaat x =1 en x =2.
Het vereiste gebied wordt gegeven door −
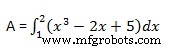
Maak een scriptbestand en typ de volgende code −
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));
Wanneer u het bestand uitvoert, wordt het volgende resultaat weergegeven −
a = 23/4 Area: 5.7500
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));
Octave voert de code uit en geeft het volgende resultaat −
Area: 5.7500
Een alternatieve oplossing kan als volgt worden gegeven met de functie quad() die door Octave wordt geleverd −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));
Octave voert de code uit en geeft het volgende resultaat −
Area: 5.7500
Voorbeeld 2
Zoek de oppervlakte onder de kromme:f(x) =x 2 cos(x) voor −4 ≤ x ≤ 9.
Maak een scriptbestand en schrijf de volgende code −
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));
Wanneer u het bestand uitvoert, plot MATLAB de grafiek −
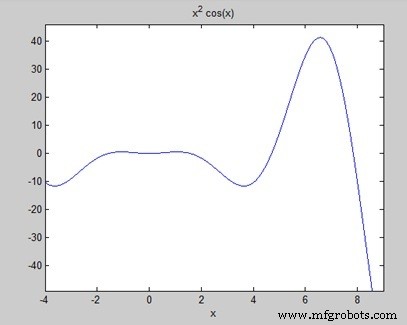
De output wordt hieronder gegeven −
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));
MATLAB