Booleaanse relaties op Venn-diagrammen

Het vierde voorbeeld heeft A gedeeltelijk overlappende B . We zullen echter eerst naar het geheel van alle gearceerde gebieden hieronder kijken, en later alleen naar het overlappende gebied. Laten we enkele Booleaanse uitdrukkingen toewijzen aan de regio's hierboven, zoals hieronder weergegeven.

Linksonder is een rood horizontaal gearceerd gebied voor A . Er is een blauw verticaal gearceerd gebied voor B .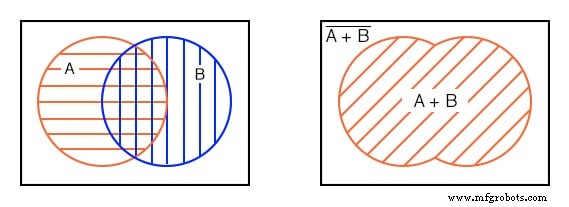

Als we naar het hele gebied van beide kijken, ongeacht de stijl van arcering, de som van alle gearceerde gebieden, krijgen we de afbeelding hierboven goed die overeenkomt met de inclusieve OF functie van A, B. De Booleaanse uitdrukking is A+B .

Dit wordt aangegeven door de 45 ^o gearceerd gebied. Alles buiten het gearceerde gebied komt overeen met (A+B)-not zoals hierboven getoond. Laten we verder gaan met het volgende deel van het vierde voorbeeld.

De andere manier om naar een Venn-diagram met overlappende cirkels te kijken, is door alleen naar het deel te kijken dat beide A gemeen hebben. en B , het dubbel gearceerde gebied linksonder. De Booleaanse uitdrukking voor dit gemeenschappelijke gebied dat overeenkomt met de AND functie is AB zoals rechtsonder weergegeven. Merk op dat alles buiten dubbel gearceerde AB is AB-niet .

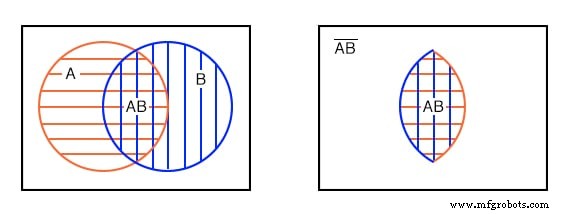
Merk op dat sommige leden van A , hierboven, zijn lid van (AB)' . Enkele leden van B zijn lid van (AB)' . Maar geen van de leden van (AB)’ bevinden zich binnen het dubbel gearceerde gebied AB .

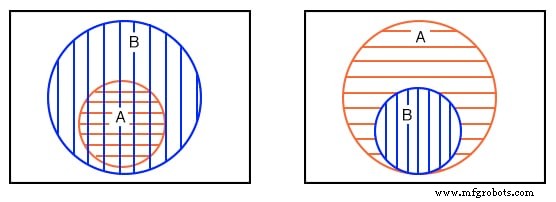
We hebben het tweede voorbeeld linksboven herhaald. Uw vijfde voorbeeld, dat u eerder schetste, staat hierboven ter vergelijking. Later zullen we het occasionele element, of een groep elementen, volledig binnen een andere groep in een Karnaugh-kaart vinden.

Vervolgens laten we hieronder de ontwikkeling zien van een Booleaanse uitdrukking met een gecomplementeerde variabele.

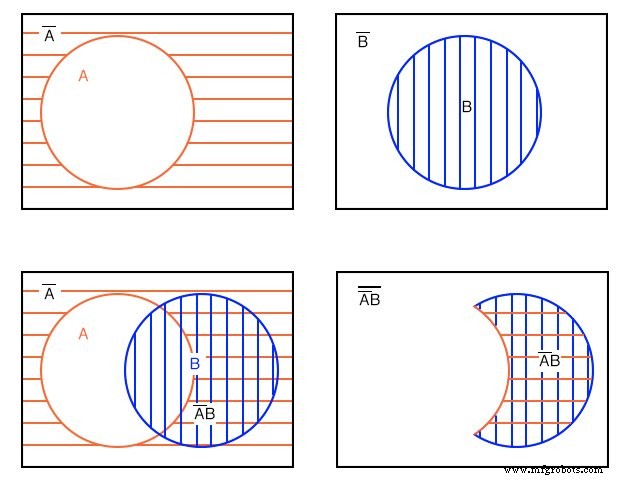
Voorbeeld: (hierboven)

Toon een Venn-diagram voor A'B (A-niet EN B).

Oplossing: Beginnend linksboven hebben we rood horizontaal gearceerd A' (A-not), dan rechtsboven B . Vervolgens vormen we linksonder de AND-functie A’B door de twee vorige regio's te overlappen. De meeste mensen zouden dit gebruiken als antwoord op het gegeven voorbeeld.

Echter, alleen de dubbel gearceerde A'B wordt voor de duidelijkheid uiterst rechts weergegeven. De uitdrukking A'B is de regio waar zowel A' en B overlappen. Het heldere gebied buiten A'B is (A'B)' , die geen deel uitmaakte van het geposeerde voorbeeld.

Laten we iets soortgelijks proberen met de Booleaanse OF functie.

Voorbeeld: Zoek B’+A

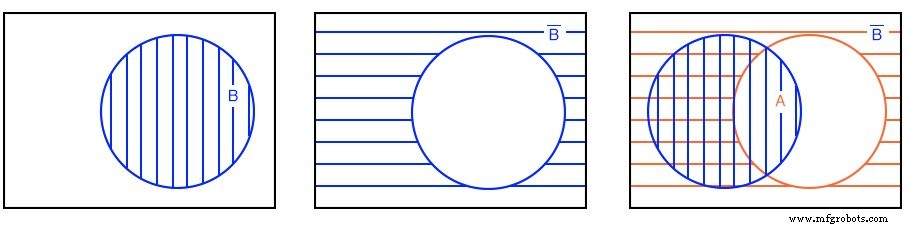
Oplossing: Rechtsboven beginnen we met B die wordt aangevuld met B' . Ten slotte overlappen we A bovenop B' . Omdat we geïnteresseerd zijn in het vormen van de OF functie, zoeken we naar alle gearceerde gebieden, ongeacht de arceringsstijl. Dus, A+B' is alle gearceerde gebied rechtsboven. Het wordt voor de duidelijkheid weergegeven als een enkel arceringgebied linksonder.

Voorbeeld: Zoek (A+B’)’

Oplossing:

De groene 45 ^o A+B' gearceerde gebied was het resultaat van het vorige voorbeeld. Doorgaan naar a tot,(A+B’)’ , laten we in het huidige voorbeeld, linksboven, het complement vinden van A+B' , wat het witte heldere gebied linksboven is dat overeenkomt met (A+B’)’ .

Merk op dat we rechts de AB' . hebben herhaald dubbel gearceerd resultaat van een eerder voorbeeld ter vergelijking met ons resultaat. De regio's die overeenkomen met (A+B')' en AB' boven links en rechts zijn identiek. Dit kan worden bewezen met de stelling van DeMorgan en dubbele ontkenning.

Dit brengt een punt naar voren. Venn-diagrammen bewijzen eigenlijk niets. Booleaanse algebra is nodig voor formele bewijzen. Venn-diagrammen kunnen echter worden gebruikt voor verificatie en visualisatie. We hebben de stelling van DeMorgan geverifieerd en gevisualiseerd met een Venn-diagram.

Voorbeeld:

Wat betekent de Booleaanse uitdrukking A’+B’ eruit zien in een Venn-diagram?

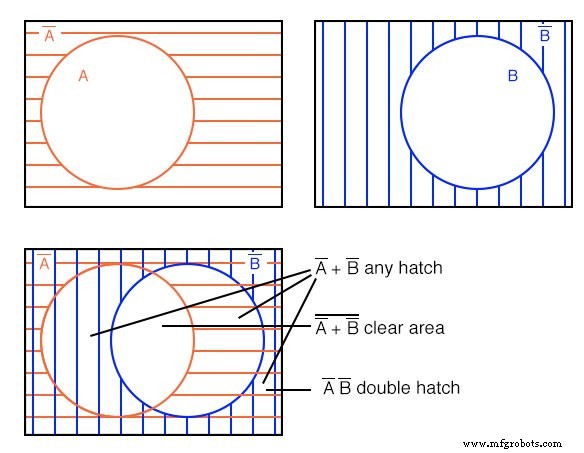
Oplossing: bovenstaande figuur

Begin met rood horizontaal gearceerd A' en blauw verticaal gearceerd B' boven. Leg de diagrammen op elkaar zoals weergegeven. We kunnen de A' . nog steeds zien rood horizontaal luik bovenop het andere luik. Het vult ook wat vroeger deel uitmaakte van de B (B-true) cirkel, maar alleen dat deel van de B open cirkel die niet gebruikelijk is bij de A open cirkel.

Als we alleen naar de B' . kijken blauw verticaal luik, het vult dat deel van de open A cirkel die niet gebruikelijk is voor B . Elke regio met enig luik, ongeacht het type, komt overeen met A'+B' . Dat wil zeggen, alles behalve de open witte ruimte in het midden.

Voorbeeld:

Wat betekent de Booleaanse uitdrukking (A’+B’)’ eruit zien in een Venn-diagram?

Oplossing: boven figuur, linksonder

Kijkend naar de witte open ruimte in het midden, is het alles NIET in de vorige oplossing van A’+B’ , dat is (A'+B')' .

Voorbeeld: Laat zien dat (A’+B’)’ =AB

Oplossing: onderstaande afbeelding, linksonder

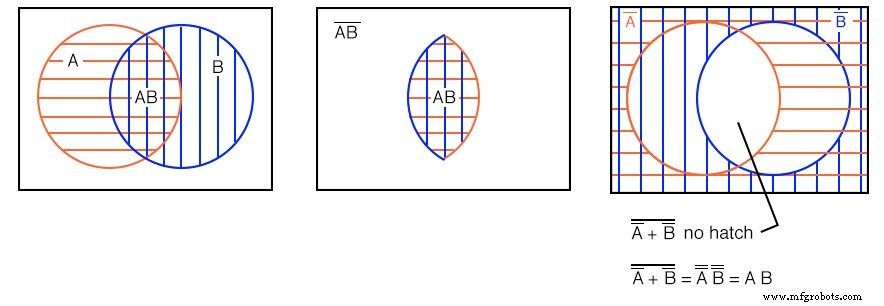
We hebben eerder in het diagram rechtsboven getoond dat het witte open gebied (A'+B')' is . Op een eerder voorbeeld toonden we een dubbel gearceerd gebied op de kruising (overlay) van AB . Dit zijn de linker- en middelste cijfers die hier worden herhaald.

Als we de twee Venn-diagrammen vergelijken, zien we dat dit open gebied , (A’+B’)’ , is hetzelfde als het dubbel gearceerde gebied AB (A EN B). We kunnen ook bewijzen dat (A’+B’)’=AB door de stelling van DeMorgan en dubbele ontkenning zoals hierboven weergegeven.

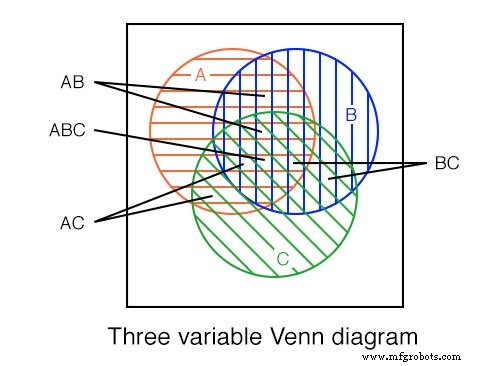
We laten hierboven een Venn-diagram met drie variabelen zien met regio's A (rood horizontaal), B (blauw verticaal), en, C (groen 45 ^o ). Merk in het midden op dat alle drie de regio's elkaar overlappen en de Booleaanse uitdrukking ABC . voorstellen .

Er is ook een groter bloembladvormig gebied waar A en B overlap die overeenkomt met Booleaanse uitdrukking AB . Op een vergelijkbare manier A en C overlap produceren Booleaanse uitdrukking AC . En B en C overlap produceren Booleaanse uitdrukking BC .

Als we kijken naar de grootte van de regio's die worden beschreven door de bovenstaande AND-expressies, zien we dat de grootte van de regio varieert met het aantal variabelen in de bijbehorende AND-expressie.

• A , 1-variabele is een groot cirkelvormig gebied.
• AB , 2-variabele is een kleiner bloembladvormig gebied.
• ABC , 3-variabele is de kleinste regio.
• Hoe meer variabelen in de AND-term, hoe kleiner de regio.