Booleaanse algebraïsche identiteiten

In de wiskunde is een identiteit is een statement waar voor alle mogelijke waarden van zijn variabele of variabelen.

De algebraïsche identiteit van x + 0 =x vertelt ons dat alles (x) toegevoegd aan nul is gelijk aan het oorspronkelijke "alles", ongeacht de waarde van dat "alles ” (x) kan zijn.

Net als gewone algebra heeft Booleaanse algebra zijn eigen unieke identiteiten op basis van de bivalente toestanden van Booleaanse variabelen.

Additieve identiteiten

Nul toevoegen

De eerste Booleaanse identiteit is dat de som van alles en nul is hetzelfde als de originele "alles .”

Deze identiteit verschilt niet van zijn algebraïsche equivalent in reële getallen:

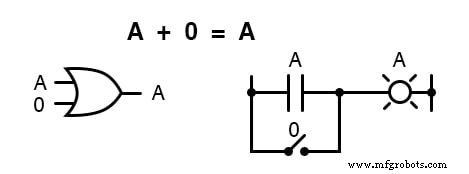
Ongeacht de waarde van A , zal de output altijd hetzelfde zijn:wanneer A=1 , zal de uitvoer ook 1 . zijn; wanneer A=0 , zal de uitvoer ook 0 . zijn .

Een toevoegen

De volgende identiteit is beslist anders dan in de normale algebra.

Hier ontdekken we dat de som van "alles ” en een is één :

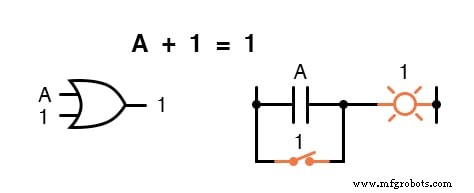
Ongeacht de waarde van A, de som van A en 1 is altijd 1.

In zekere zin, het "1"-signaal overschrijft het effect van A op het logische circuit, waarbij de uitgang vast blijft op een logisch niveau van 1.

Een hoeveelheid aan zichzelf toevoegen

Vervolgens onderzoeken we het effect van het toevoegen van A en A samen, wat hetzelfde is als het verbinden van beide ingangen van een OF-poort naar elkaar toe en activeer ze met hetzelfde signaal:

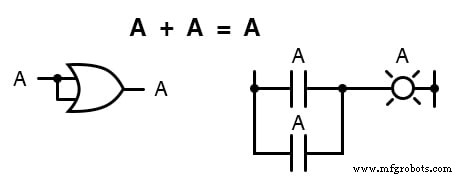
In reële-getalalgebra is de som van twee identieke variabelen tweemaal de waarde van de oorspronkelijke variabele (x + x =2 x), maar onthoud dat er geen concept van "2" is in de wereld van Booleaanse wiskunde, alleen 1 en 0, dus we kunnen niet zeggen dat A + A =2A .

Dus als we een Booleaanse hoeveelheid bij zichzelf optellen, is de som gelijk aan de oorspronkelijke hoeveelheid:0 + 0 =0 , en 1 + 1 =1 .

Een hoeveelheid toevoegen aan de aanvulling

Door het unieke Booleaanse concept van complementatie in een additieve identiteit te introduceren, vinden we een interessant effect.

Aangezien er één "1 . moet zijn ” waarde tussen elke variabele en zijn complement, en aangezien de som van elke Booleaanse hoeveelheid en 1 1 is, moet de som van een variabele en zijn complement 1:

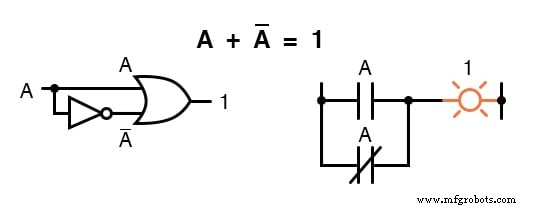
Multiplicatieve identiteiten

Net zoals er vier Booleaanse additieve identiteiten zijn (A+0, A+1, A+A en A+A' ), dus er zijn ook vier multiplicatieve identiteiten:Ax0, Ax1, AxA en AxA' . Hiervan verschillen de eerste twee niet van hun equivalente uitdrukkingen in de reguliere algebra:

Vermenigvuldigen met 0 of 1

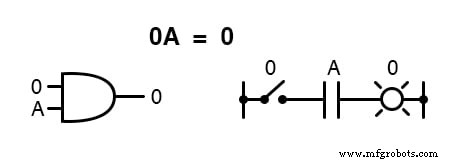
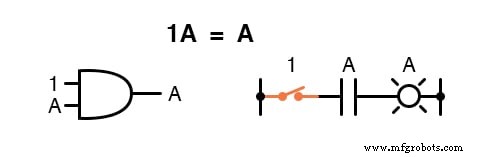
Een hoeveelheid met zichzelf vermenigvuldigen

De derde multiplicatieve identiteit drukt het resultaat uit van een Booleaanse hoeveelheid vermenigvuldigd met zichzelf.

In normale algebra is het product van een variabele en zichzelf het vierkant van die variabele (3 x 3 =3 ² =9).

Het concept van vierkant impliceert een hoeveelheid van 2, wat geen betekenis heeft in Booleaanse algebra, dus we kunnen niet zeggen dat A x A =A ² .

In plaats daarvan vinden we dat het product van een Booleaanse hoeveelheid en zichzelf de oorspronkelijke hoeveelheid is, aangezien 0 x 0 =0 en 1 x 1 =1 :

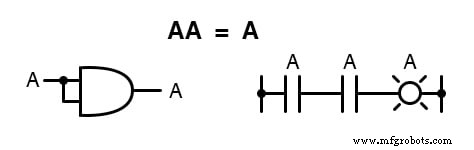
Een hoeveelheid vermenigvuldigen met zijn complement

De vierde multiplicatieve identiteit heeft geen equivalent in reguliere algebra omdat het het complement van een variabele gebruikt, een concept dat uniek is voor Booleaanse wiskunde.

Aangezien er één “0 . moet zijn ” waarde tussen elke variabele en zijn complement, en aangezien het product van elke Booleaanse hoeveelheid en 0 is 0 , het product van een variabele en zijn complement moet 0 . zijn :

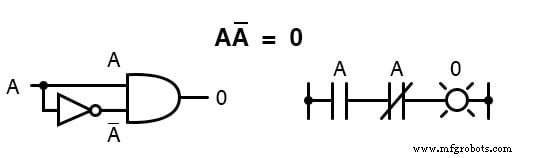
Samenvattend hebben we dus vier basis Booleaanse identiteiten voor optellen en vier voor vermenigvuldiging:

Dubbele aanvulling

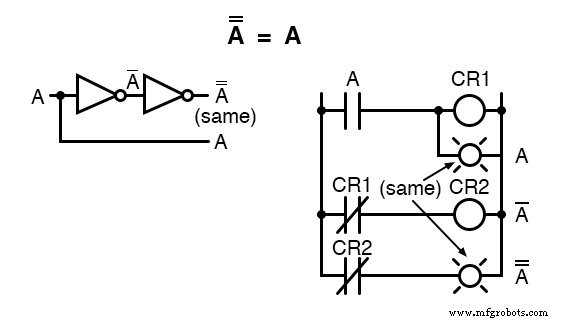
Een andere identiteit die met complementatie te maken heeft, is die van de dubbele aanvulling :een variabele die tweemaal wordt geïnverteerd.

Als je een variabele twee keer (of een even aantal keren) aanvult, krijg je de oorspronkelijke Booleaanse waarde.

Dit is analoog aan ontkenning (vermenigvuldigen met -1) in algebra met reële getallen:een even aantal ontkenningen annuleert om de oorspronkelijke waarde te behouden:

GERELATEERDE WERKBLAD:

• Booleaanse algebra-werkblad