Booleaanse rekenkunde

Laten we onze verkenning van Booleaanse algebra beginnen door getallen bij elkaar op te tellen:

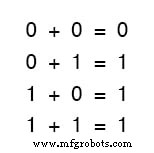
De eerste drie sommen zijn volkomen logisch voor iedereen die bekend is met elementaire optelling.

De laatste som is echter mogelijk verantwoordelijk voor meer verwarring dan enige andere verklaring in digitale elektronica, omdat het in strijd lijkt te zijn met de basisprincipes van de wiskunde.

Wel, het is in tegenspraak met de principes van optellen voor reële getallen, maar niet voor Booleaanse getallen.

Onthoud dat er in de wereld van de Booleaanse algebra slechts twee mogelijke waarden zijn voor elke hoeveelheid en voor elke rekenkundige bewerking:1 of 0.

Er bestaat niet zoiets als "2" binnen het bereik van Booleaanse waarden. Aangezien de som "1 + 1" zeker niet 0 is, moet het 1 zijn door het proces van eliminatie.

Het maakt ook niet uit hoeveel of weinig termen we bij elkaar optellen. Overweeg de volgende sommen:

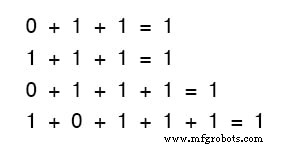
OF-poort

Bekijk de sommen van twee termen in de eerste reeks vergelijkingen eens goed.

Komt dat patroon je bekend voor? Het zou moeten! Het is hetzelfde patroon van enen en nullen als in de waarheidstabel voor een OF-poort.

Met andere woorden, Booleaanse optelling komt overeen met de logische functie van een "OF"-poort, evenals met parallelle schakelcontacten:

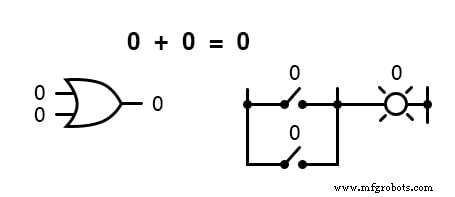
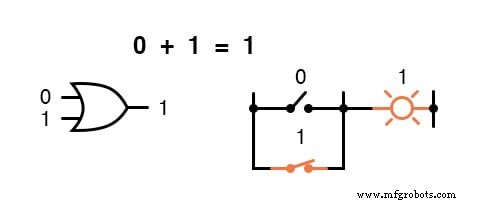
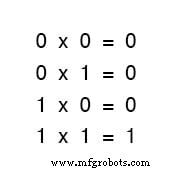
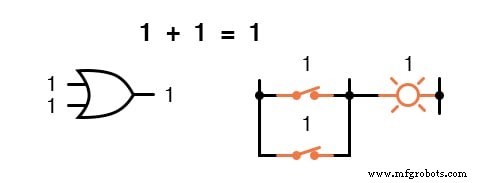
Er bestaat niet zoiets als aftrekken op het gebied van Booleaanse wiskunde.

Aftrekken impliceert het bestaan ​​van negatieve getallen:5 - 3 is hetzelfde als 5 + (-3) , en in Booleaanse algebra zijn negatieve grootheden verboden.

Er bestaat ook niet zoiets als delen in Booleaanse wiskunde, aangezien delen eigenlijk niets meer is dan samengestelde aftrekking , op dezelfde manier waarop vermenigvuldiging samengestelde optelling is .

EN-poort

Vermenigvuldiging is geldig in Booleaanse algebra, en gelukkig is het hetzelfde als in reële algebra:alles vermenigvuldigd met 0 is 0 , en alles vermenigvuldigd met 1 blijft ongewijzigd:

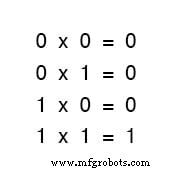
Deze reeks vergelijkingen zou u ook bekend moeten voorkomen:het is hetzelfde patroon als in de waarheidstabel voor een EN-poort.

Met andere woorden, Booleaanse vermenigvuldiging komt overeen met de logische functie van een “EN ” poort, evenals naar serieschakelcontacten:

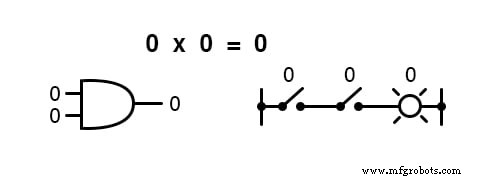
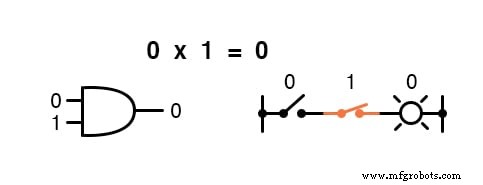
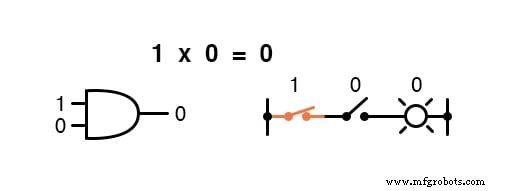
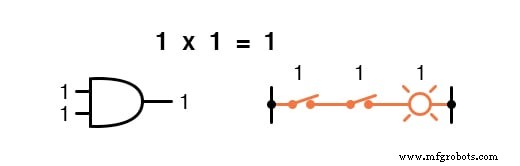
Net als "normale" algebra, gebruikt Booleaanse algebra alfabetische letters om variabelen aan te duiden.

In tegenstelling tot "normale" algebra zijn Booleaanse variabelen echter altijd HOOFDLETTERS, nooit kleine letters.

Omdat ze slechts één van de twee mogelijke waarden mogen bezitten, ofwel 1 of 0 , elke variabele heeft een complement :het tegenovergestelde van zijn waarde.

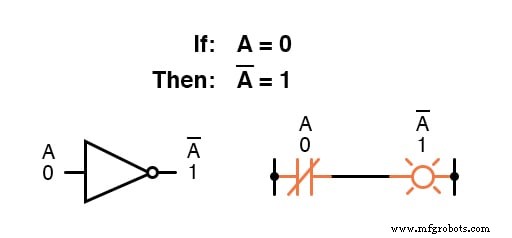
Als variabele "A . bijvoorbeeld ” heeft een waarde van 0 , dan het complement van A heeft een waarde van 1 .

Booleaanse notatie gebruikt een balk boven het variabele teken om complementatie aan te duiden, zoals deze:

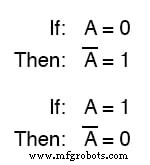
NIET poort

In geschreven vorm, het complement van “A ” aangeduid als “A-not ” of “A-balk ”. Soms wordt een "prime"-symbool gebruikt om complementatie aan te geven.

Bijvoorbeeld A ’ zou de aanvulling zijn van A , ongeveer hetzelfde als het gebruik van een prime-symbool om differentiatie in calculus aan te duiden in plaats van de fractionele notatie d/dt .

Meestal wordt het "bar"-symbool echter meer wijdverbreid gebruikt dan de "prime ” symbool, om redenen die later in dit hoofdstuk duidelijk zullen worden.

Booleaanse complementatie vindt equivalentie in de vorm van de NIET-poort , of een normaal gesloten schakelaar of relaiscontact:

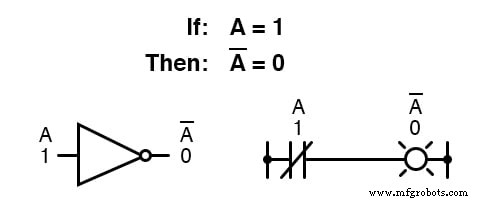
De basisdefinitie van Booleaanse grootheden heeft geleid tot de eenvoudige regels van optellen en vermenigvuldigen, en heeft zowel aftrekken als delen uitgesloten als geldige rekenkundige bewerkingen.

We hebben een symbologie voor het aanduiden van Booleaanse variabelen en hun complementen. In de volgende sectie gaan we verder met het ontwikkelen van Booleaanse identiteiten.

BEOORDELING:

• Booleaanse toevoeging is gelijk aan de OF logische functie, evenals parallelle schakelcontacten.
• Booleaanse vermenigvuldiging is gelijk aan de AND logische functie, evenals serieschakelcontacten.
• Booleaanse complementatie is gelijk aan de NIET logische functie, evenals normaal gesloten relaiscontacten.

GERELATEERDE WERKBLAD:

• Booleaanse algebra-werkblad