Booleaanse regels voor vereenvoudiging

Booleaanse algebra vindt zijn meest praktische toepassing in de vereenvoudiging van logische circuits.

Als we de functie van een logisch circuit vertalen in symbolische (Booleaanse) vorm, en bepaalde algebraïsche regels toepassen op de resulterende vergelijking om het aantal termen en/of rekenkundige bewerkingen te verminderen, kan de vereenvoudigde vergelijking terug worden vertaald in circuitvorm voor een logisch circuit dat dezelfde functie met minder componenten.

Als een gelijkwaardige functie kan worden bereikt met minder componenten, zal het resultaat een grotere betrouwbaarheid en lagere fabricagekosten zijn.

Hiertoe worden in deze sectie verschillende regels van Booleaanse algebra gepresenteerd die kunnen worden gebruikt bij het reduceren van uitdrukkingen tot hun eenvoudigste vormen.

De identiteiten en eigenschappen die al in dit hoofdstuk zijn besproken, zijn erg nuttig bij Booleaanse vereenvoudiging, en vertonen voor het grootste deel gelijkenis met veel identiteiten en eigenschappen van "normale" algebra.

De regels die in deze sectie worden getoond, zijn echter allemaal uniek voor Booleaanse wiskunde.

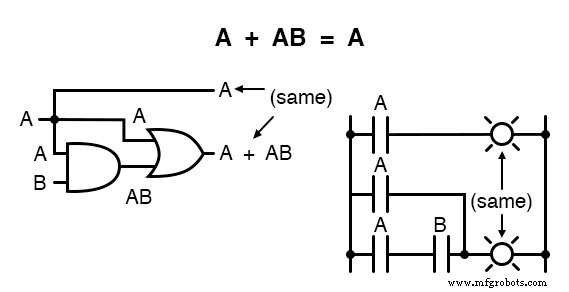
Deze regel kan symbolisch worden bewezen door een "A" uit de twee termen te ontbinden en vervolgens de regels van A + 1 =1 en 1A =A toe te passen om het eindresultaat te bereiken:

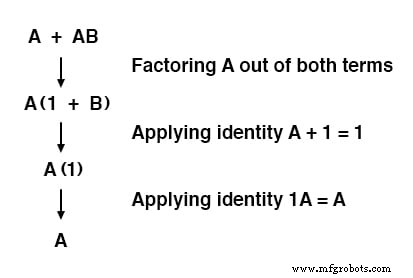
Merk op hoe de regel A + 1 =1 werd gebruikt om de (B + 1) term te reduceren tot 1.

Wanneer een regel als "A + 1 =1" wordt uitgedrukt met de letter "A", betekent dit niet dat deze alleen van toepassing is op uitdrukkingen die "A" bevatten.

Waar de "A" voor staat in een regel als A + 1 =1 is een Booleaanse variabele of verzameling variabelen.

Dit is misschien wel het moeilijkste concept voor nieuwe studenten om onder de knie te krijgen in Booleaanse vereenvoudiging:gestandaardiseerde identiteiten, eigenschappen en regels toepassen op uitdrukkingen die niet in standaardvorm zijn.

De Booleaanse uitdrukking ABC + 1 reduceert bijvoorbeeld ook tot 1 door middel van de identiteit "A + 1 =1".

In dit geval erkennen we dat de "A"-term in de standaardvorm van de identiteit de volledige "ABC"-term in de oorspronkelijke uitdrukking kan vertegenwoordigen.

De volgende regel lijkt op de eerste die in deze sectie wordt getoond, maar is in werkelijkheid heel anders en vereist een slimmer bewijs:

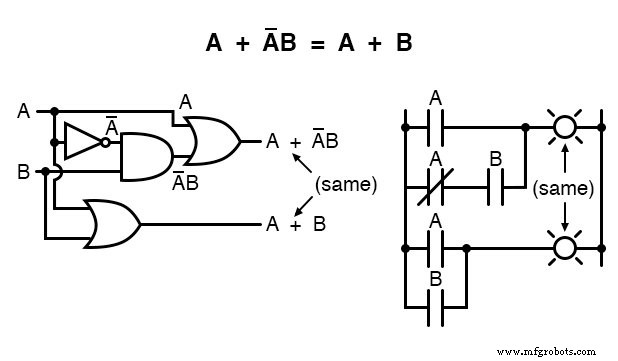
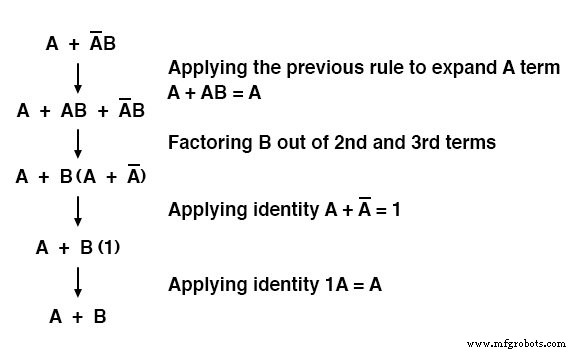
Merk op hoe de laatste regel (A + AB =A) wordt gebruikt om de eerste "A"-term in de uitdrukking te "vereenvoudigen" en de "A" te veranderen in een "A + AB".

Hoewel dit misschien een stap achteruit lijkt, heeft het zeker geholpen om de uitdrukking terug te brengen tot iets eenvoudigers!

Soms moeten we in de wiskunde "achterwaartse" stappen nemen om tot de meest elegante oplossing te komen.

Weten wanneer je zo'n stap moet zetten en wanneer niet, maakt deel uit van de kunstvorm van de algebra, net zoals een overwinning in een schaakspel bijna altijd berekende opofferingen vereist.

Een andere regel betreft de vereenvoudiging van een product-van-sommen-uitdrukking:

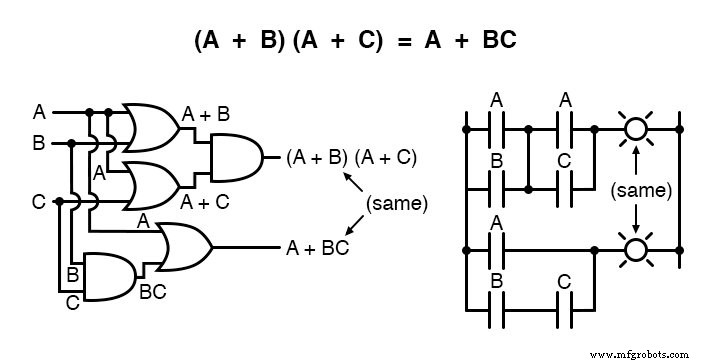
En het bijbehorende bewijs:

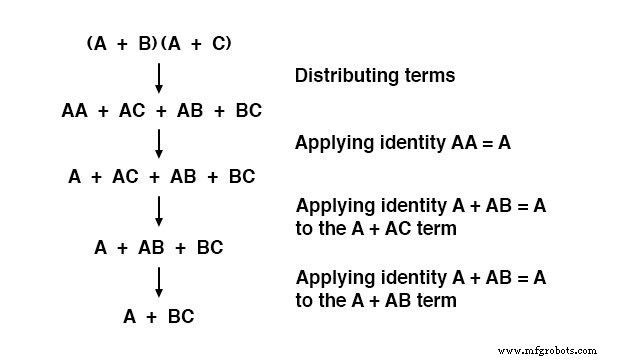
Om samen te vatten, hier zijn de drie nieuwe regels van Booleaanse vereenvoudiging uiteengezet in deze sectie:

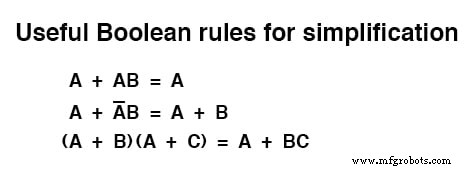
GERELATEERDE WERKBLAD:

• Booleaanse algebra-werkblad