Booleaanse algebraïsche eigenschappen
Een ander type wiskundige identiteit, een 'eigenschap' of een 'wet' genoemd, beschrijft hoe verschillende variabelen zich tot elkaar verhouden in een systeem van getallen.
De commutatieve eigenschap
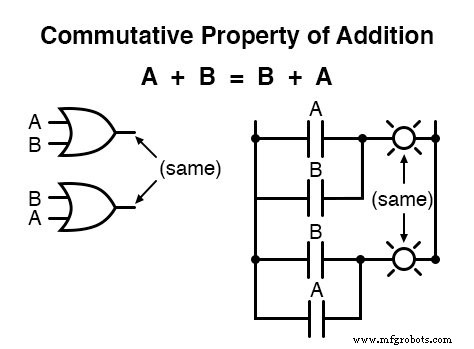
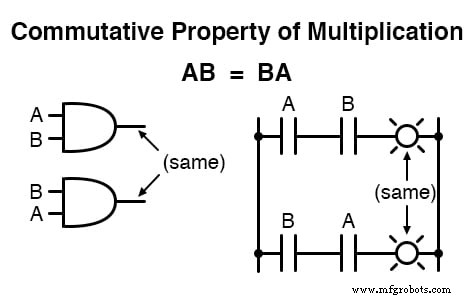
Een van deze eigenschappen staat bekend als de commutatieve eigenschap , en het is gelijkelijk van toepassing op optellen en vermenigvuldigen.
In wezen vertelt de commutatieve eigenschap ons dat we de volgorde van variabelen die bij elkaar opgeteld of vermenigvuldigd zijn, kunnen omkeren zonder de waarheid van de uitdrukking te veranderen:
De associatieve eigenschap
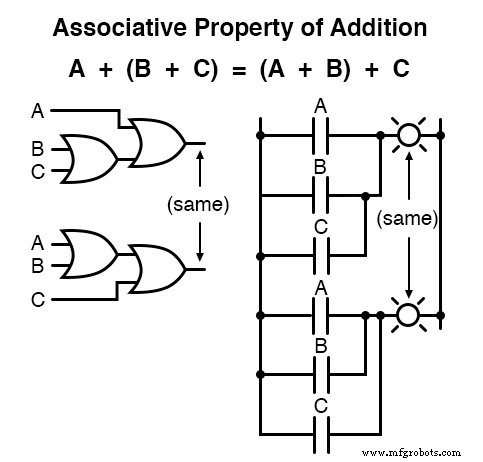
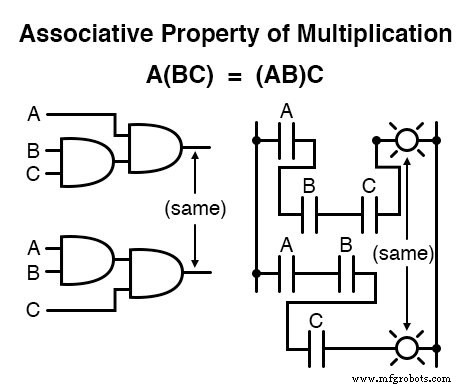
Naast de commutatieve eigenschappen van optellen en vermenigvuldigen, hebben we de associatieve eigenschap , opnieuw even goed van toepassing op optellen en vermenigvuldigen.
Deze eigenschap vertelt ons dat we groepen toegevoegde of vermenigvuldigde variabelen kunnen associëren met haakjes zonder de waarheid van de vergelijkingen te veranderen.
De distributieve eigenschap
Ten slotte hebben we de verdelende eigenschap , illustreert hoe een Booleaanse uitdrukking gevormd door het product van een som kan worden uitgebreid, en laat ons omgekeerd zien hoe termen kunnen worden ontbonden uit Booleaanse productsommen:
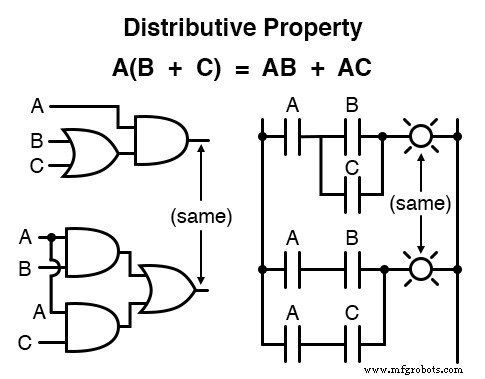
Samenvattend zijn hier de drie basiseigenschappen:commutatief, associatief en distributief.

GERELATEERDE WERKBLAD:
- Booleaanse algebra-werkblad
Industriële technologie



