Een Venn-diagram eruit laten zien als een Karnaugh-kaart

Beginnend met cirkel A in een rechthoekig A'-universum in figuur (a) hieronder veranderen we een Venn-diagram in bijna een Karnaugh-kaart.

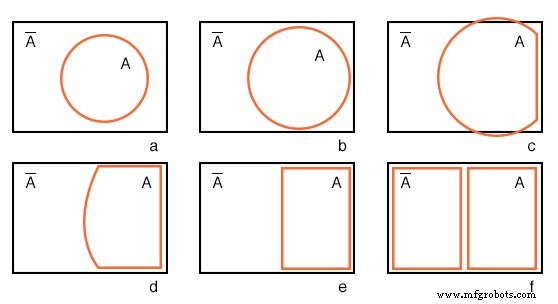
We vergroten cirkel A bij (b) en (c), conform het rechthoekige A'-universum bij (d), en verander A naar een rechthoek bij (e). Alles buiten A is A' . We kennen een rechthoek toe aan A' bij (f). Ook gebruiken we geen arcering in Karnaugh-kaarten. Wat we tot nu toe hebben, lijkt op een 1-variabele Karnaugh-kaart, maar is van weinig nut. We hebben meerdere variabelen nodig.

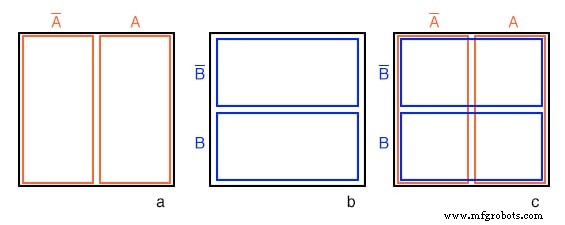
Afbeelding (a) hierboven is hetzelfde als het vorige Venn-diagram met A en A' hierboven, behalve dat de labels A en A' bevinden zich boven het diagram in plaats van binnen de respectieve regio's. Stel je voor dat we een proces hebben doorlopen dat vergelijkbaar is met figuren (a-f) om een ​​"vierkant Venn-diagram" te krijgen voor B en B' zoals we laten zien in middelste figuur (b).

We zullen nu de diagrammen in de figuren (a) en (b) over elkaar heen leggen om het resultaat bij (c) te krijgen, net zoals we hebben gedaan voor Venn-diagrammen. De reden dat we dit doen, is dat we kunnen waarnemen wat twee overlappende regio's gemeen hebben:zeg waar A overlapt B . De cel rechtsonder in figuur (c) komt overeen met AB waar A overlapt B .

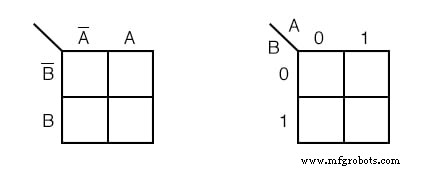
We verspillen geen tijd met het tekenen van een Karnaugh-kaart zoals (c) hierboven, maar schetsen in plaats daarvan een vereenvoudigde versie zoals hierboven links. De kolom van twee cellen onder A' wordt verondersteld geassocieerd te zijn met A' , en de kop A wordt geassocieerd met de kolom met cellen eronder. De rij aangevoerd door B' is gekoppeld aan de cellen rechts ervan.

Op een vergelijkbare manier B wordt geassocieerd met de cellen rechts ervan. Voor de eenvoud hebben we de verschillende regio's niet zo duidelijk afgebakend als bij Venn-diagrammen.

De Karnaugh-kaart rechtsboven is een alternatieve vorm die in de meeste teksten wordt gebruikt. De namen van de variabelen staan ​​naast de diagonale lijn.

De A boven de diagonaal geeft aan dat de variabele A (en A' ) is toegewezen aan de kolommen. De 0 is een vervanging voor A' , en de 1 vervangt A . De B onder de diagonaal hoort bij de rijen:0 voor B' , en 1 voor B

Voorbeeld:

Markeer de cel die overeenkomt met de Booleaanse uitdrukking AB in de Karnaugh-kaart hierboven met een 1

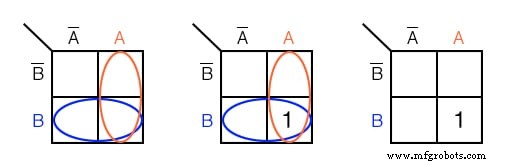
Oplossing:

Schaduw of omcirkel het gebied dat overeenkomt met A . Verduister of omsluit vervolgens het gebied dat overeenkomt met B . De overlap van de twee regio's is AB . Plaats een 1 in deze cel. We plaatsen niet noodzakelijk de A en B regio's zoals linksboven.

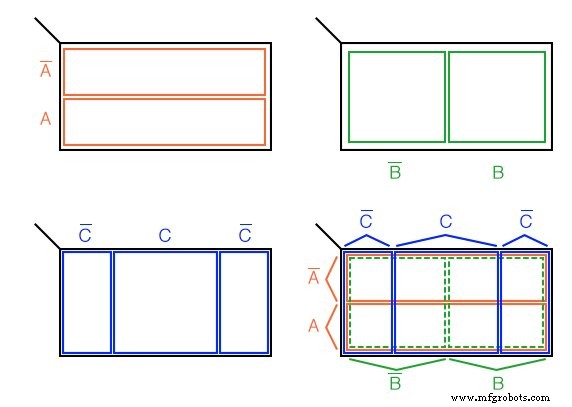
K-map met 3 variabelen

We ontwikkelen hierboven een Karnaugh-kaart met 3 variabelen, te beginnen met Venn-diagramachtige regio's. Het universum (binnen de zwarte rechthoek) is gesplitst in twee smalle, smalle rechthoekige gebieden voor A' en A . De variabelen B’ en B verdeel het heelal in twee vierkante gebieden. C bezet een vierkant gebied in het midden van de rechthoek, met C’ opgesplitst in twee verticale rechthoeken aan elke kant van de C vierkant.

In de laatste figuur leggen we alle drie de variabelen op elkaar en proberen we de verschillende regio's duidelijk te labelen. De regio's zijn minder duidelijk zonder afdrukken in kleur, meer duidelijk in vergelijking met de andere drie figuren.

Deze 3-variabele K-Map (Karnaugh-kaart) heeft 2 ³ =8 cellen , de kleine vierkantjes op de kaart. Elke individuele cel wordt uniek geïdentificeerd door de drie Booleaanse variabelen (A, B, C ). Bijvoorbeeld ABC' selecteert op unieke wijze de meest rechtse cel(*), A'B'C' selecteert de meest linkse cel (x).

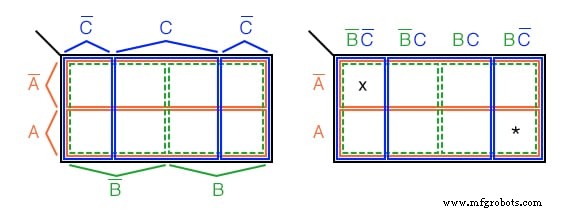
Normaal gesproken labelen we de Karnaugh-kaart niet zoals linksboven weergegeven. Hoewel deze afbeelding duidelijk de kaartdekking laat zien door enkelvoudige booleaanse variabelen van een 4-cels gebied.

Karnaugh-kaarten zijn gelabeld zoals de afbeelding rechts. Elke cel wordt nog steeds uniek geïdentificeerd door een productterm met 3 variabelen , een Booleaanse EN uitdrukking. Neem bijvoorbeeld ABC' na de A rij naar rechts en de BC' kolom omlaag, beide kruisen elkaar rechtsonder in cel ABC' . Zie (*) bovenstaande afbeelding.

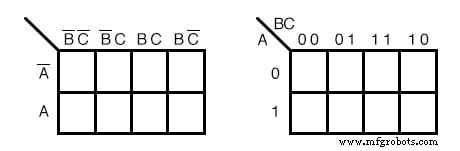
De bovenstaande twee verschillende vormen van een Karnaugh-kaart met 3 variabelen zijn equivalent en is de uiteindelijke vorm die het aanneemt. De versie aan de rechterkant is een beetje gemakkelijker te gebruiken, omdat we niet zoveel booleaanse alfabetische kopteksten en complementaire balken hoeven op te schrijven, alleen 1s en 0s Gebruik de vorm van de kaart aan de rechterkant en zoek die aan de linkerkant in sommige teksten . De kolomkoppen aan de linkerkant B’C’, B’C, BC, BC’ zijn gelijk aan 00, 01, 11, 10 aan de rechterkant. De rijkoppen A, A' zijn gelijk aan 0, 1 op de rechterkaart.