Venn-diagrammen en sets

Wiskundigen gebruiken Venn-diagrammen om de logische relaties van sets te tonen (verzamelingen objecten) aan elkaar. Misschien heb je al Venn-diagrammen gezien in je algebra- of andere wiskundestudies. Als je dat hebt gedaan, herinner je je misschien overlappende cirkels en de vakbond en kruispunt reeksen.

We zullen de overlappende cirkels van het Venn-diagram bekijken. We zullen de termen OR en AND gebruiken in plaats van unie en intersectie, aangezien dat de terminologie is die wordt gebruikt in digitale elektronica.

Het Venn-diagram vormt een brug tussen de Booleaanse algebra uit een vorig hoofdstuk en de Karnaugh-kaart. We zullen wat u al weet over Booleaanse algebra relateren aan Venn-diagrammen en vervolgens overschakelen naar Karnaugh-kaarten.

Een set is een verzameling objecten uit een universum zoals hieronder weergegeven. De leden van de set zijn de objecten in de set. De leden van de set hebben meestal iets gemeen; dit is echter geen vereiste.

Uit het universum van reële getallen, bijvoorbeeld, is de verzameling van alle positieve gehele getallen {1,2,3...} een verzameling. De set {3,4,5} is een voorbeeld van een kleinere set, of subset van de verzameling van alle positieve gehele getallen. Een ander voorbeeld is de verzameling van alle mannen uit het universum van studenten. Kun je nog meer voorbeelden van sets bedenken?

Linksboven hebben we een Venn-diagram met daarin de verzameling A in de cirkel binnen het heelal U, het rechthoekige gebied. Als alles binnen de cirkel A is, dan is alles buiten de cirkel niet A. Dus, boven het midden, labelen we het rechthoekige gebied buiten de cirkel A als A-niet in plaats van U. We tonen B en B-niet in een vergelijkbare manier.

Wat gebeurt er als zowel A als B zich in hetzelfde universum bevinden? We laten vier mogelijkheden zien.

Laten we elk van de vier mogelijkheden, zoals hierboven weergegeven, nader bekijken.

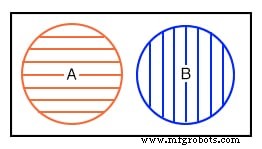
Het eerste voorbeeld laat zien dat set A en set B niets gemeen hebben volgens het Venn-diagram. Er is geen overlap tussen de A en B cirkelvormige gearceerde gebieden. Stel bijvoorbeeld dat sets A en B de volgende leden bevatten:

stel A ={1,2,3,4} in stel B ={5,6,7,8} 

Geen van de leden van set A bevindt zich in set B, en ook geen van de leden van B binnen A. Er is dus geen overlap van de cirkels.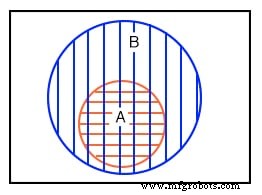

In het tweede voorbeeld in het bovenstaande Venn-diagram, is set A volledig opgenomen in set B. Hoe kunnen we deze situatie verklaren? Stel dat sets A en B de volgende leden bevatten:

stel A ={1,2} in stel B ={1,2,3,4,5,6,7,8} 

Alle leden van set A zijn ook leden van set B. Daarom is set A een subset van set B. Aangezien alle leden van set A lid zijn van set B, wordt set A volledig binnen de grens van set B getrokken.

Er is een vijfde geval, niet getoond, met de vier voorbeelden. Hint:het is vergelijkbaar met het laatste (vierde) voorbeeld. Teken een Venn-diagram voor dit vijfde geval.

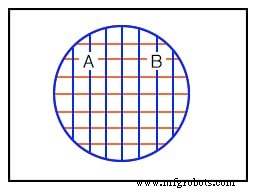
Het derde voorbeeld hierboven laat een perfecte overlap zien tussen set A en set B. Het lijkt erop dat beide sets dezelfde identieke leden bevatten. Stel dat sets A en B het volgende bevatten:

stel A ={1,2,3,4} in stel B ={1,2,3,4} 

Daarom,

Set A =Set B

Sets en B zijn identiek gelijk omdat ze allebei dezelfde identieke leden hebben. De A- en B-regio's binnen het corresponderende Venn-diagram hierboven overlappen elkaar volledig. Als er enige twijfel bestaat over wat de bovenstaande patronen vertegenwoordigen, raadpleeg dan een afbeelding hierboven of hieronder om er zeker van te zijn hoe de cirkelvormige gebieden eruit zagen voordat ze elkaar overlappen.

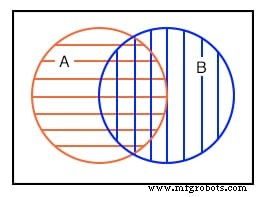
Het vierde voorbeeld hierboven laat zien dat er iets gemeen is tussen set A en set B in het overlappende gebied. We selecteren bijvoorbeeld willekeurig de volgende sets om ons punt te illustreren:

stel A ={1,2,3,4} in stel B ={3,4,5,6} 

Set A en Set B hebben beide de elementen 3 en 4 gemeen. Deze elementen zijn de reden voor de overlap in het centrum die A en B gemeen hebben. We moeten deze situatie nader bekijken.