Basisprincipes van PID-regeling en lusafstemming

De industriële sector is sterk afhankelijk van PID-controllers voor alle soorten automatiseringsbehoeften. A regellus is een fundamenteel feedbackmechanisme dat is ingesteld om de kloof tussen de gemeten procesvariabele en het gewenste setpoint te overbruggen. Controllers worden gebruikt om de juiste corrigerende inspanningen toe te passen via interfaces, actuatoren genaamd, die de variabele omhoog of omlaag kunnen sturen. De controller past de corrigerende inspanning in een lus toe, totdat de fout tot de gewenste nauwkeurigheid is geëlimineerd.

Geschiedenis

Toen de eerste feedbackcontrollers in productie kwamen, waren ze alleen ontworpen met de proportionele term. Al snel realiseerde men zich echter dat alleen P-controllers de fout alleen naar beneden konden brengen tot een verwaarloosbare maar toch niet-nulwaarde. Dit vereiste dat de operators de versterking handmatig moesten instellen totdat het laatste foutspoor was verwijderd.

Om dit laatste stukje actie automatisch uit te voeren, werd de integrale term geïntroduceerd, die vaak automatische reset wordt genoemd vanwege zijn vermogen om de proportionele actie aan te passen. Kort daarna werd de afgeleide term geïntroduceerd en werd deze beschreven als een snelheidscontrole, die fungeerde als een ruwe voorspeller van fouten die kunnen optreden op basis van de huidige fouthelling.

PID-basis

Een PID-controller maakt gebruik van de volgende formule om zijn output te berekenen, d.w.z. u(t), terwijl e(t) het foutsignaal is, dat het verschil is tussen de procesvariabele en het setpoint.

PID-controllers hebben een aantal termen die ermee verbonden zijn; deze omvatten:

• Gain – dit verwijst naar het percentage waarmee het foutsignaal aan kracht wint of verliest als het door de verschillende blokken van de controllers gaat, helemaal naar de uitgang. Als een PID-controller bijvoorbeeld is ingesteld op high-gain, zou deze op agressieve wijze corrigerende maatregelen nemen om de fout te verwijderen.
• Integrale tijd – Een hypothetische reeks gebeurtenissen kan ertoe leiden dat het foutsignaal abrupt naar een vaste waarde springt, wat een onmiddellijke reactie van de proportionele term van de controller en een gestaag toenemende respons van de integrale term zou legitimeren. De tijd die de integraalterm nodig heeft om de onveranderlijke proportionele tijd in te halen, is de integrale tijd en wordt aangeduid met TI.
• Afgeleide tijd – Als een fout bij nul begint en met een vaste snelheid toeneemt, zou de proportionele term ook bij nul beginnen, terwijl de afgeleide term een ​​vaste waarde zou aannemen. De afgeleide tijd, TD, is een maat voor de relatieve invloed van de afgeleide term, wat betekent dat een PID-regelaar met een lange afgeleide tijd een zwaardere afgeleide actie zou uitvoeren dan een proportionele.

Lus afstemmen

Vaak aangeduid als een kunst, betekent lusafstemming van een PID-controller het selecteren van waarden voor de afstemparameters, d.w.z. P, TI en TD, zodat de controller de fout in een respectabele hoeveelheid tijd zou kunnen elimineren, zonder al te veel fluctuaties te veroorzaken .

De cruisecontroller van een auto is daar een mooi voorbeeld van. Telkens wanneer een auto start, voegt zijn traagheid een vertraging toe tussen het moment dat het gaspedaal werd ingedrukt en het moment waarop de gewenste snelheid wordt bereikt. De afgeleide en proportionele acties van de controller mogen in dit geval niet onmiddellijk in werking treden, maar op een manier die niet te oncomfortabel is voor de passagiers of moeilijk is voor de interne machineonderdelen. Als de vertraging bij het bereiken van de gewenste snelheid te lang is, zou de integrale actie ook van pas komen en de output van de controller domineren.

Het instellen van de drie parameters is niet eenvoudig omdat ze alle drie onderling afhankelijk zijn, wat betekent dat het wijzigen van een ervan ook de prestaties van de andere twee zou beïnvloeden.

Ziegler-Nichols Tuning

In 1942 bedachten John G. Ziegler en Nathaniel B. Nicholas, die bij Taylor Instruments werkten, een interessante methode om problemen met de lusafstemming op te lossen.

Hun open-lustechniek houdt in dat de controller een offline stappentest doorloopt, waarna een curve genaamd reactiecurve wordt geplot op basis van de resultaten. Op het steilste punt van de curve wordt een raaklijn getekend die informatie geeft over hoe snel het proces reageert op een stapsgewijze verandering. Beiden kwamen tot de volgende conclusie:

• De procestijdconstante, T, is de inverse van de helling van de raaklijn.
• De dode tijd, d, is de tijd die het proces nodig heeft om zijn eerste reactie op de stap aan te tonen.
• De proceswinst, K, geeft aan hoeveel de procesvariabele toeneemt ten opzichte van de grootte van de stap.

Uiteindelijk bedachten Ziegler &Nicholas formules die hen waarden gaven voor de drie parameters, namelijk P, TI en TD van T, d en K. De formules zijn:

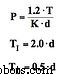
Zodra deze parameters in de PID-formule zijn geladen en de regelaar in de automatische status is gezet, zijn er geen verdere onderbrekingen nodig om fouten of fluctuaties te elimineren.

Toch is PID-lusafstemming geen eenvoudig proces en vereist herhalingen wanneer de aard van het proces op enigerlei wijze verandert. Dit is de reden waarom loop-tuning een kunst wordt genoemd en een combinatie van ervaring en geluk vereist, in plaats van ruwe wiskundige vaardigheden!

Geïnteresseerd in meer informatie? Praat met een van onze professionals op PanelShop.com .