Een ontwikkelde uitdrukking van chemisch potentieel voor snelle vervorming in nanodeeltjeselektroden van lithium-ionbatterijen

Methoden

Mechanische vergelijkingen

Het inbrengen van lithium in elektroden kan volumetrische verandering veroorzaken. Voor het gemak gebruiken we twee manieren om de vervorming en beweging van de vaste stoffen te beschrijven, namelijk de Lagrangiaanse beschrijving en de Euleriaanse beschrijving. De beweging van materiële deeltjes in een continuüm kan worden beschreven door

waar x is de Euler-coördinaten, X is de Lagrange-coördinaten, en U is het verplaatsingsveld. De verandering in de vorm van het continuüm vaste stof kan worden gekenmerkt door de vervormingsgradiënt tensor, gegeven door

waarbij Grad de gradiëntoperator vertegenwoordigt in de Lagrangiaanse beschrijving, en I is de eenheidstensor van de tweede orde.

Voor een bolvormig deeltje zijn de Lagrange-coördinaten en de Euler-coördinaten van een materieel punt (R, Θ, Φ) en (r, θ, ) respectievelijk in het bolvormige systeem. Dan is de vervormingsgradiënt tensor F wordt gevonden als

Tijdens het laden of ontladen kan de vormverandering van de elektrode in twee processen worden verdeeld:(a) een vormverandering door het inbrengen van lithium en (b) een omkeerbare elastische vervorming. Deze twee vervormingsprocessen kunnen worden beschreven door twee gescheiden gradiënttensoren en de totale vervormingsgradiënttensor kan worden geschreven als

waar F ^e vertegenwoordigt de elastische vervorming, F ^c vertegenwoordigt de vormverandering als gevolg van het invoegen van lithium. Vergelijking (4) vertegenwoordigt het proces van elektrodemateriaal van de initiële (niet-vervormde) toestand naar de huidige (vervormde) toestand. Ervan uitgaande dat de vormverandering als gevolg van het invoegen van lithium isotroop is, F ^c kan worden gegeven door

waarbij Ω staat voor het partiële molaire volume.

Van verg. (3–5), de elastische vervormingsgradiënt tensor F ^e is

De totale Green-Lagrange-rektensor E kan worden geschreven als

waarbij de elastische spanningstensor E ^e en door diffusie geïnduceerde spanningstensor E ^c zijn

respectievelijk.

Vervanging van Eq. (6) in Vgl. (8), de radiale en tangentiële componenten van de Green-Lagrange-rektensor zijn

De constitutieve relatie voor de vervorming kan worden bepaald uit de rekenergiedichtheid als

waar W is de elastische spanningsenergiedichtheid in de Lagrangiaanse beschrijving, en P is de eerste Piola-Kirchhoff-spanning. Bovendien, als het materiaal lineair elastisch is, W kan worden geschreven als een kwadratische functie van de Green-Lagrange-rektensor

Hier, E _h en ν zijn respectievelijk Young's modulus en Poisson's ratio, C is de stijfheidstensor, en det(F ^c ) is de determinant van de vervormingsgradiënttensor voor de door diffusie geïnduceerde vervorming.

Ten slotte wordt de eerste Piola-Kirchhoff-spanning gegeven door

Combineren van vergelijkingen. (5), (9), (10) en (13), de overeenkomstige componenten van de eerste Piola-Kirchhoff (P-K) spanningstensor zijn

En de eerste P-K spanning moet voldoen aan de evenwichtsvoorwaarde bij afwezigheid van lichaamskracht

met begin- en randvoorwaarden

Vergelijking massavervoer

De concentratie en de diffusieflux van lithium in elektroden, die functies zijn van coördinaten en tijd, zullen C worden genoemd. (X , t) en J (X , t) in de Lagrangiaanse beschrijving, en ze moeten tevreden zijn met de massatransportvergelijking geschreven als

waarbij Div de divergentie-operator in de Lagrangiaanse beschrijving vertegenwoordigt. Gezien het kenmerk van sferische symmetrie, vindt diffusie alleen plaats in radiale richting en gebruiken we J (R , t) om de radiale component van J . weer te geven (X , t). In het bolvormige systeem, Vgl. (18) wordt

De diffusie van lithium in elektroden wordt aangedreven door een chemische potentiaalgradiënt en de radiale flux J (R , t) is evenredig met de gradiënt van de chemische potentiaal μ , als [11]

waar D is de diffusiviteit, R _g is de gasconstante, en T is de temperatuur. μ wordt gedefinieerd als de afwijking van de totale energiedichtheid tot de concentratie en kan worden geschreven als

Neem aan dat de energiedichtheid van het systeem, Π, beschreven kan worden als de som van de chemische energiedichtheid en de rekenergiedichtheid. Dus de totale interne energiedichtheid kan worden geschreven als

Vervanging van Eq. (22) in Vgl.(21), de chemische potentiaal μ kan worden aangetoond dat het

waar μ ₀ (C ) en τ (E ^e , C ) zijn respectievelijk de spanningsonafhankelijke en spanningsafhankelijke delen van de chemische potentiaal. En

waar μ ₀ is een constante die de chemische potentiaal in een standaardtoestand vertegenwoordigt, en γ is de activiteitscoëfficiënt die de effecten van interacties tussen de atomen/moleculen weergeeft. Voor een verdunde oplossing zijn interacties tussen de atomen/moleculen verwaarloosbaar; dus, γ = 1.

We concentreren ons op het stressafhankelijke deel van de chemische potentiaal τ (E ^e , C), wat de afgeleide is van de rekenergiedichtheid W met betrekking tot de concentratie van lithium C. Traditioneel, Π(X , t) wordt beschouwd als Helmholtz vrije energiedichtheid en daarom wordt deze stap uitgevoerd voor vaste vervorming geschreven als [11]

Het subscript H betekent dat het wordt veroorzaakt door de vrije energiedichtheid van Helmholtz. Het chemische potentieel blijkt

waar σ _m is de Cauchy hydrostatische spanning in Euleriaanse beschrijving en kan worden verkregen door

Het is de moeite waard om op te merken dat de stijfheid C van het elektrodemateriaal wordt verondersteld onafhankelijk te zijn van de concentratie van lithium C in verg. (12). Bovendien, det(F ^e ) ≈ 1 wordt algemeen aanvaard, zodat het meestal wordt genegeerd. In de rest van dit artikel noemen we Vgl. (26) als de traditionele uitdrukking van chemisch potentieel. Aan de andere kant, Π(X , t) wordt in sommige onderzoeken [12, 13] op faseveldmodel beschouwd als de Gibbs-vrije energiedichtheid, zodat we geen ontwikkelde uitdrukking van τ kunnen krijgen (E ^e , C), en

Het onderschrift G betekent dat het wordt veroorzaakt door de Gibbs vrije energiedichtheid. In dit geval μ wordt

en we noemen Vgl. (29) als de ontwikkelde uitdrukking van chemisch potentieel.

De massatransportvergelijking bestaat uit Vgl. (19), (20), (26) en (29) met traditionele en ontwikkelde uitdrukkingen van chemisch potentieel. In het resterende deel van dit artikel zullen we de effecten van deze twee uitdrukkingen van chemisch potentieel op de door diffusie geïnduceerde stress en Li-concentratie onder verschillende oplaadmethoden vergelijken.

In de thermodynamica is de Helmholtz-vrije energie een thermodynamisch potentieel dat het nuttige werk meet dat kan worden verkregen uit een gesloten thermodynamisch systeem bij een constante temperatuur en volume. Daarentegen meet de Gibbs vrije energie het maximum aan omkeerbare arbeid die kan worden uitgevoerd door een thermodynamisch systeem bij een constante temperatuur en druk. In vaste stoffen met een laag spanningsniveau is de Gibbs-vrije energie ongeveer gelijk aan de Helmholtz-vrije energie, omdat de vervorming van vaste stoffen meestal klein is. Deze aanname is geschikt voor de meeste vaste materialen vanwege hun kleine door diffusie geïnduceerde vervorming, maar behalve voor silicium vanwege de grote volumetrische uitzetting tijdens lithiëring. In feite vinden diffusie en vervorming tegelijkertijd plaats, zodat het niet passend is aan te nemen dat er geen vervorming optreedt terwijl de concentratie verandert. Toch, zoals blijkt uit Vgl. (25) is de traditionele uitdrukking van chemisch potentieel nog steeds nauwkeurig wanneer de vervormingssnelheid laag genoeg is. Het is echter waarschijnlijk dat het grote fouten veroorzaakt wanneer een Si-nanodeeltjeselektrode snel wordt gelithieerd.

De elektrode wordt gelithieerd met een constante lithium-ionconcentratie op het oppervlak, namelijk de potentiostatische werking, of met een constante flux op het oppervlak, namelijk de galvanostatische werking. De randvoorwaarden van Vgl. (19) zijn

respectievelijk. De beginvoorwaarde wordt geschreven als

voor elke laadoperatie. Hier, C _max is de maximale lithiumconcentratie van het materiaal en j ₀ is een constante die de laadstroom weergeeft.

Numerieke implementatie

Het is erg moeilijk om de analytische oplossing van het bovenstaande systeem, bestaande uit partiële differentiaalvergelijkingen, te verkrijgen, zo niet onmogelijk. Met eq. (1)–(3) en (13)–(18), berekenen we de evolutie van door diffusie geïnduceerde stress en lithiumconcentratie numeriek met behulp van de COMSOL multiphysics-software. De lithiatie van een silicium nano-elektrode onder zowel potentiostatische als galvanostatische operaties wordt bestudeerd, met verschillende uitdrukkingen van chemisch potentieel. De materiaaleigenschappen van Si en de bedrijfsparameters die in de simulatie worden gebruikt, staan ​​vermeld in Tabel 1. Voor het gemak is in de figuren de corresponderende dimensieloze substitutie van coördinaat, spanning en concentratie gebruikt.

Om het verschil tussen de verschillende uitdrukkingen van chemische potentiaal op verschillende tijdstippen in de bolvormige Si-elektrode te onderzoeken, wordt de ladingstoestand (SOC) berekend als

De door spanning geïnduceerde diffusiefluxen in de Lagrangiaanse beschrijving worden beschreven als

die respectievelijk de flux vertegenwoordigen die wordt veroorzaakt door verschillende chemische potentiaaluitdrukkingen.

Resultaten en discussie

Figuur 1 toont de ruimtelijke verdeling van de concentratie van lithium, radiale spanning en ringspanning in een bolvormige Si-elektrode onder galvanostatische werking bij verschillende SOC's. Ter vergelijking zijn de numerieke resultaten met zowel de ontwikkelde als de traditionele uitdrukkingen van chemisch potentieel opgenomen en worden ze weergegeven door respectievelijk ononderbroken lijnen en driehoekige symbolen. Voor elke SOC in figuur 1a overlapt de ononderbroken lijn bijna de driehoekssymbolen. Het effect dat wordt veroorzaakt door de verschillende uitdrukkingen van chemische potentiaal op de concentratie van lithium kan worden genegeerd. In Fig. 1b en Fig. 1c zijn voor de SOC's van 46,7% en 65,5% de ononderbroken lijnen hoger dan de driehoeken in het midden, terwijl ze buiten bijna overlappen, net als bij andere SOC's. Over het algemeen is er een gering effect op de concentratie van lithium en spanningen bij galvanostatisch bedrijf. Figuur 2 toont de ruimtelijke verdelingen van de concentratie van lithium, radiale spanning en ringspanning in een bolvormige Si-elektrode onder potentiostatische werking bij verschillende SOC's. Het is vermeldenswaard dat de radiale en hoepelspanningen eerst toenemen en vervolgens afnemen met de toename van SOC in zowel figuur 1 als figuur 2. Het is omdat de siliciumelektrode in de begintoestand of volledig gelithieerde toestand spanningsvrij is, omdat er geen concentratiegradiënt is. In vergelijking met figuur 1a is het verschil tussen ononderbroken lijnen en driehoeken groter in figuur 2a. Door de lithiumconcentratie op het oppervlak is er een constante C _max onder potentiostatische werking is de laadsnelheid hoger dan de vervormingssnelheid die van galvanostatische werking en ook de vervormingssnelheid. De totale vervorming onder dezelfde SOC is echter bijna hetzelfde, ongeacht de oplaadmethode, maar neemt alleen een andere tijd in beslag. Het geeft aan dat de invloed op de verdeling van lithium veroorzaakt door verschillende uitdrukkingen van chemische potentiaal alleen gerelateerd is aan de vervormingssnelheid in plaats van de vervorming en toeneemt met de toename van de vervormingssnelheid. In feite tonen bestaande experimenten aan dat siliciumelektroden zeer snel vervormen tijdens lithiëring onder bepaalde oplaadmodi. Zoals we kunnen zien in Fig. 3 [17], is de Si-anode volledig vervormd in 1 minuut met een 2-V-potentiaal ten opzichte van het Li-metaal. In deze toestand zullen de resultaten die door deze twee uitdrukkingen van chemisch potentieel worden opgelost, aanzienlijk verschillen. Helaas kan in dit geval de spanning van de elektrode niet nauwkeurig worden gemeten en daarom niet kwantitatief worden vergeleken met ons model.

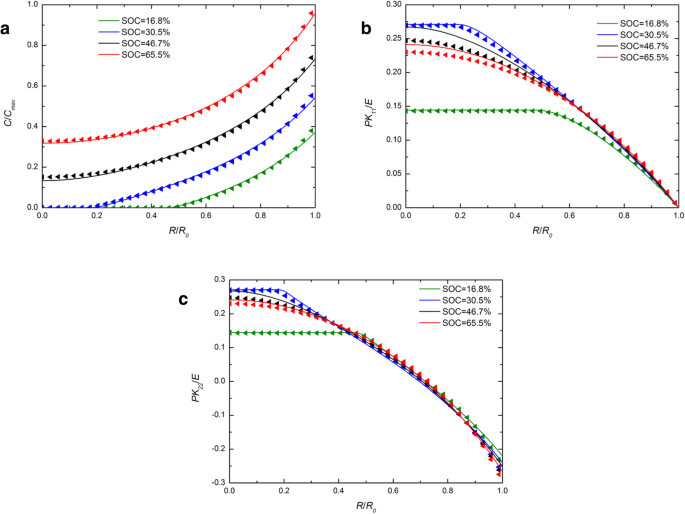
Ruimtelijke verdeling van (a ) de concentratie lithium, (b ) radiale spanning, en (c ) ringspanning in een bolvormige Si-elektrode bij verschillende SOC's onder galvanostatische werking (ononderbroken lijnen vertegenwoordigen de resultaten met de traditionele uitdrukking van chemisch potentieel; driehoekige lijnen vertegenwoordigen de resultaten met de ontwikkelde uitdrukking van chemisch potentieel)

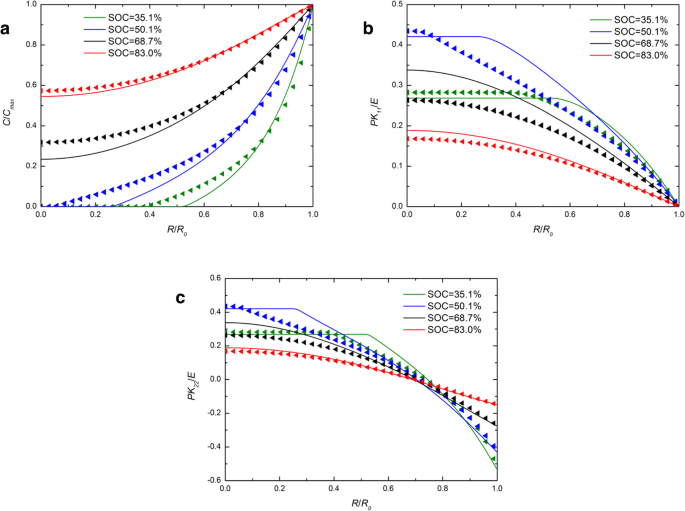
Ruimtelijke verdeling van (a ) de concentratie lithium, (b ) radiale spanning, en (c ) hoepelspanning in een bolvormige Si-nanodeeltjeselektrode bij verschillende SOC's onder potentiostatische werking (ononderbroken lijnen vertegenwoordigen de resultaten met de traditionele uitdrukking van chemisch potentieel; driehoekige lijnen vertegenwoordigen de resultaten met de ontwikkelde uitdrukking van chemisch potentieel)

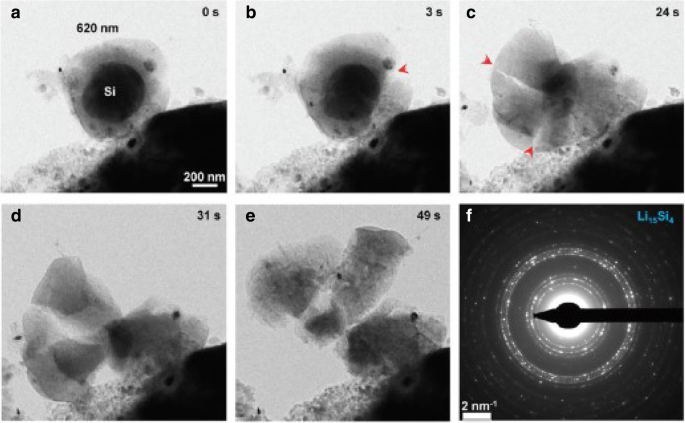
Snelle vervorming van een vrijstaande 620-nm SiNP tijdens chemische lithiëring in 1 minuut. een –e Tijdsvolgorde van scheurinitiatie en groei. v EDP ​​die de vorming van polykristallijn Li₁₅ . aangeeft Si₄ als de volledig gelithieerde fase

Figuur 4 toont de ruimtelijke verdeling van J _H /J _G in een bolvormige Si-elektrode bij verschillende SOC's onder galvanostatische werking met verschillende j . In Fig. 4 vallen de ononderbroken lijnen bijna samen met de driehoeken, wat aangeeft dat verschillende chemische potentiaaluitdrukkingen een klein effect hebben op de verhouding van J _H en J _G . Het is duidelijk dat het bereik van de waarden van J _H /J _G neemt toe met de toename van de laadstroom. Dit komt omdat de grotere laadstroom leidt tot hogere vervormingssnelheden en daarom de grotere impact van verschillende uitdrukkingen van chemische potentiaal veroorzaakt. De verhouding is altijd groter dan 1 in het midden en kleiner dan 1 op het oppervlak. Het suggereert dat de flux verkregen uit de ontwikkelde uitdrukking van chemisch potentieel op het oppervlak groter is dan die verkregen uit de traditionele uitdrukking, terwijl het tegenovergestelde waar is in het centrum. We merken op dat alle ononderbroken lijnen en driehoeken in figuur 4 elkaar bijna snijden in één punt. Bovendien is de verhouding die overeenkomt met het snijpunt altijd ongeveer 1, ongeacht met welke stroom de elektrode wordt geladen. Het suggereert dat er een kritische straal is waar de flux minder wordt beïnvloed door de verschillende chemische potentiaaluitdrukkingen. We noemen het de chemische potentiaalonafhankelijke regio (CIR). Het is duidelijk dat CIR zich altijd in de buurt van het oppervlak van de bolvormige elektrode bevindt en dichter bij het oppervlak naarmate de laadstroom toeneemt.

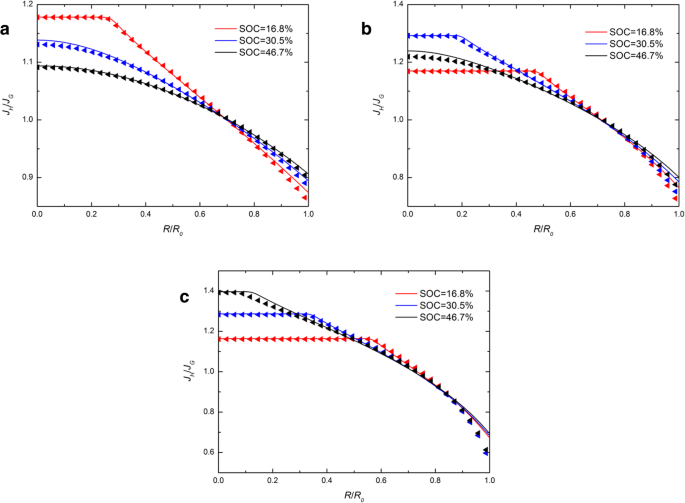
Ruimtelijke verdeling van J _H /J _G in een bolvormige Si-nanodeeltjeselektrode bij verschillende SOC's onder galvanostatische werking met (a ) j =0,5j ₀ , (b ) j =j ₀ , en (c ) j =1.5j ₀ (ononderbroken lijnen vertegenwoordigen de resultaten met de traditionele uitdrukking van chemisch potentieel; driehoekige lijnen vertegenwoordigen de resultaten met de ontwikkelde uitdrukking van chemisch potentieel)

Door de traditionele en ontwikkelde chemische potentialen in Vgl. (26) en vgl. (29) blijkt dat de Cauchy hydrostatische spanning σ_m is de sleutel tot het verschil tussen deze twee uitdrukkingen. Om de oorzaken van CIR te onderzoeken, is de ruimtelijke verdeling van σ_m /E in een bolvormige Si-elektrode bij verschillende SOC's onder galvanostatische werking met verschillende uitdrukkingen van chemisch potentieel worden gegeven in Fig. 5 en Fig. 6. Het is duidelijk dat bijna alle curven elkaar kruisen op één punt in CIR en de Cauchy hydrostatische spanning σ _m is op dit punt bijna 0, behalve aan het begin van het opladen (SOC =6,2%). Het geeft aan dat σ_m in CIR wordt gedurende het grootste deel van de oplaadperiode op een laag niveau (bijna 0) gehouden. Het kan worden geïnterpreteerd dat de twee chemische potentiaaluitdrukkingen bijna equivalent zijn wanneer de hydrostatische spanning σ_m ligt dicht bij 0. Dit kan gedeeltelijk verklaren waarom CIR verschijnt, maar het is niet voldoende om de kenmerken van krommen op σ_m uit te leggen . Het moet worden opgelost door ons volgende onderzoek.

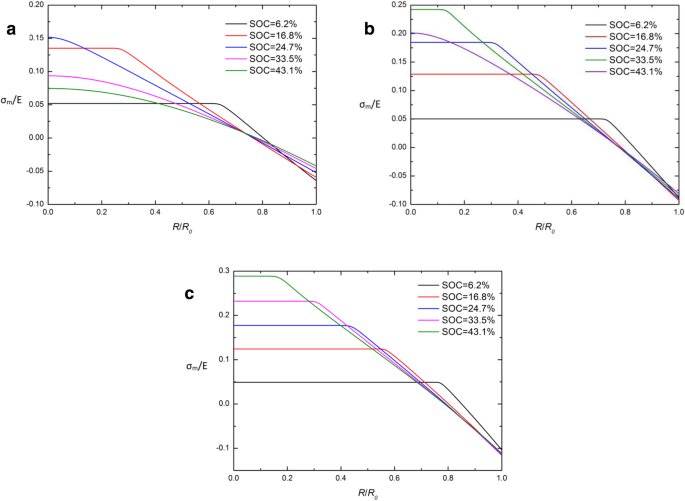
Ruimtelijke verdeling van σ _m /E in een bolvormige Si-nanodeeltjeselektrode bij verschillende SOC's onder galvanostatische werking met de traditionele uitdrukking van chemisch potentieel en (a ) j =0,5j ₀ , (b ) j =j _0, en (c ) j =1.5j ₀

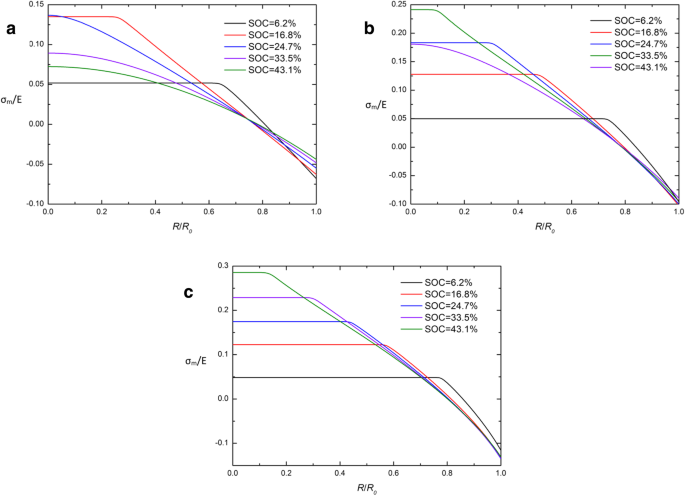
Ruimtelijke verdeling van σ _m /E in een bolvormige Si-nanodeeltjeselektrode bij verschillende SOC's onder galvanostatische werking met de ontwikkelde uitdrukking van chemisch potentieel (a ) j =0,5j ₀ , (b ) j =j ₀ , en (c ) j =1.5j ₀ s

Conclusies

In dit werk wordt een ontwikkelde uitdrukking van chemisch potentieel voorgesteld zonder de aanname van lage vervormingssnelheid, die zich onderscheidt van de ontwikkelde uitdrukking die momenteel veel wordt gebruikt. Het verschil tussen de traditionele en ontwikkelde uitdrukkingen van chemische potentiaal op de verdelingen van spanning en concentratie in Si-nanodeeltjeselektroden wordt besproken onder zowel potentiostatische als galvanostatische bewerkingen.

Het resultaat laat zien dat het effect veroorzaakt door verschillende uitdrukkingen van chemische potentiaal verwaarloosd kan worden bij galvanostatische werking, maar significant is bij potentiostatische werking. Het is gebleken dat het effect alleen verband houdt met de vervormingssnelheid in plaats van met de vervorming, en het kan groter zijn naarmate de vervormingssnelheid toeneemt. Gezien de aanname van lage vervormingssnelheid in de traditionele chemische potentiaalexpressie, wordt aangenomen dat de resultaten die worden verkregen door de ontwikkelde chemische potentiaalexpressie betrouwbaarder zijn. Een chemisch potentiaalonafhankelijk gebied (CIR), waar de flux veroorzaakt door traditioneel en ontwikkeld chemisch potentieel bijna hetzelfde is tijdens het grootste deel van het gelithieerde proces, wordt gevonden nabij het oppervlak van de nanodeeltjeselektrode. Bovendien is CIR dichter bij het oppervlak met de toename van de laadstroom. Een soortgelijk fenomeen doet zich ook voor in de Cauchy hydrostatische spanningscurven. De Cauchy hydrostatische spanning σ_m houdt een constante en gehandhaafd op een laag niveau (bijna 0) in CIR op de meeste tijd, ongeacht welke chemische potentiaalexpressie wordt gebruikt. Dergelijke resultaten zijn nog niet gerapporteerd in de literatuur.

Beschikbaarheid van gegevens en materialen

De datasets die tijdens het huidige onderzoek zijn geanalyseerd, zijn op redelijk verzoek verkrijgbaar bij de corresponderende auteur.

Afkortingen

CIR:

Een regio waar de diffusieflux veroorzaakt door deze twee uitdrukkingen van chemisch potentieel bijna hetzelfde is