Invloed van dislocaties op de brekingsindex van AlN door rekveld op nanoschaal
Abstract
De brekingsindex van AlN heeft een directe invloed op op AlGaN gebaseerde diep-ultraviolette opto-elektronische apparaten, zoals de externe kwantumefficiëntie van lichtemitterende apparaten. Het onthullen van de afhankelijkheid van de brekingsindex van AlN van de threading-dislocaties is zinvol omdat threading-dislocaties met hoge dichtheid meestal voorkomen in AlN. In dit artikel wordt het effect van verschillende dislocatiedichtheden op de brekingsindex van AlN onderzocht. Met de toename van dislocatiedichtheden van 4,24 × 10 8 tot 3,48 × 10 9 cm − 2 , neemt de brekingsindex van AlN af van 2.2508 naar 2.2102 bij 280 nm. Verder onderzoek toont aan dat het spanningsveld op nanoschaal rond dislocaties de voortplanting van licht verandert en dus de brekingsindex van AlN verlaagt. Deze studie zal gunstig zijn voor het ontwerp van opto-elektronische apparaten en dus voor het realiseren van hoogwaardige diep-ultraviolette opto-elektronische apparaten.
Inleiding
Op AlN gebaseerde materialen zijn veelbelovende materialen voor de fabricage van diep ultraviolet (DUV) opto-elektronische apparaten zoals light-emitting diodes (LED's) [1,2,3,4,5], laserdiodes [6,7,8] en fotodetectoren [ 9, 10] vanwege de directe bandgap die kan worden afgesteld van 3,4 tot 6,2 eV [11]. De brekingsindex van AlN heeft direct effecten op de prestaties van de opto-elektronische apparaten. Voor LED's heeft de brekingsindex van AlN invloed op de lichtextractie-efficiëntie (LEE), omdat de totale interne reflectiehoek wordt bepaald door het verschil van de brekingsindex tussen de AlN-laag en een ander gebied, wat de belangrijkste beperkende factor is voor de hoeveelheid van lichtopbrengst. Aangezien de externe kwantumefficiëntie (EQE) het product is van de interne kwantumefficiëntie en de LEE, zal de brekingsindex van AlN de EQE van LED's beïnvloeden. Ook speelt de brekingsindex een sleutelrol bij het ontwerp van golfgeleiderstructuren zoals gedistribueerde Bragg-reflector (DBR) [12,13,14], waarvan de reflectiviteit gevoelig is voor de brekingsindex. Daarom is het belangrijk om de factoren te onthullen die de brekingsindex van AlN beïnvloeden. Uit eerdere studies kan worden geleerd dat de brekingsindex van AlN kan worden beïnvloed door vele factoren, waaronder temperatuur, druk en bandgap. De brekingsindex van AlN neemt toe met hogere temperatuur [15] en lagere druk [16]. Voor op AlN gebaseerd materiaal wordt de brekingsindex lager met de toename van de bandgap [17]. Ook hebben de dislocaties in halfgeleiders grote invloed op de eigenschappen van halfgeleiders en de prestaties van apparaten. De dislocaties zullen de spanning in materialen vrijgeven [18]. Ze zullen ook de donkerstroom en responsiviteit van de fotodetectoren beïnvloeden [19] en het IQE van meerdere kwantumbronnen [11, 20] enzovoort beïnvloeden. Er zijn echter maar weinig onderzoeken gericht op de invloed van verschillende threading dislocatiedichtheden (TDD's) op de brekingsindex van AlN, hoewel er hoge TDD's zijn in AlN-materialen, die gewoonlijk variëren van 10 8 tot 10 9 cm − 2 bestellingen uit recente rapporten [21,22,23]. Onderzoek naar de correlatie tussen TDD's en de brekingsindex van AlN is de sleutel om de prestaties van de opto-elektronische apparaten te optimaliseren. In dit artikel is de afhankelijkheid van verschillende TDD's van de brekingsindex van AlN bestudeerd. De verschillende fotongolflengten worden gebruikt, zoals 633 nm, 365 nm en 280 nm. De resultaten laten zien dat de dislocaties leiden tot een afname van de brekingsindex van AlN. De resultaten zullen ten goede komen aan het ontwerp en de simulatie van op AlN gebaseerde opto-elektronische apparaten zoals DUV-LED's en DBR-structuren.
Methoden
Om de relatie tussen dislocaties en de brekingsindex van AlN te bestuderen, werden AlN-templates gekweekt door metaal-organische chemische dampafzetting (MOCVD) op c-saffiersubstraten en vervolgens uitgegloeid bij verschillende temperaturen om AlN-monsters met verschillende dislocatiedichtheden te verkrijgen.
Bij het kweken van AlN-templates door MOCVD werden trimethylaluminium en ammoniak gebruikt als voorlopergassen. Als draaggas werd waterstof gebruikt. De druk tijdens de groei werd op 40 mbar gehouden. De groeitemperatuur en -tijd van de kiemlaag is ongeveer 955 ° C gedurende 150 ° s en vervolgens verhoogd tot 1280 ° C voor hoge temperatuur (HT) AlN-groei. Na 15 minuten AlN-groei bij hoge temperatuur, werd een AlN-tussenlaag gedurende 160 s bij 1050 ° C gekweekt. Ten slotte werd de groeitemperatuur verhoogd tot 1280 °C om gedurende 50 min dik HT AlN te laten groeien. De totale dikte van AlN-film is ongeveer 1,1 m.
Na de groei van de AlN-laag door MOCVD, werden de AlN-templates ex situ gegloeid bij respectievelijk 1500 ° C, 1600 ° C, 1700 ° C en 1750 ° C gedurende 1 uur. De AlN-laag zonder uitgloeien werd gemarkeerd als monster 1 en de monsters na 1500 ° C tot 1750 ° C uitgloeien werden gemarkeerd als monsters 2 tot 5. De röntgendiffractie (XRD) werd gebruikt om de TDD's in AlN-monsters te meten, en de spectroscopische ellipsometrische (SE) meting werd genomen om de brekingsindex te meten. De Raman-verschuivingsspectra werden gebruikt om de spanningstoestand van AlN-sjablonen te karakteriseren.
Resultaten en discussie
Figuur 1 a en b tonen de (0002) en (10-12) vlakke XRD-schommelcurven (XRC) van de vijf AlN-monsters. Er kan worden waargenomen dat de volledige breedte bij half maximum (FWHM) van (0002) vlak XRC lichtjes afneemt en de FWHM van (10-12) vlak XRC sterk afneemt van monster 1 tot monster 5. De dichtheid van dislocaties met schroef en rand component kan worden berekend met behulp van de FWHM van (0002) en (10–12) vlak XRC volgens formule (1) en (2):[24, 25].
$$ {\rho}_{\mathrm{s}}={\beta_{(0002)}}^2/\left(2\pi \ln 2\times {\left|{b}_c\right|} ^2\right) $$ (1) $$ {\rho}_{\mathrm{e}}={\beta_{\left(10-12\right)}}^2/\left(2\pi \ ln 2\times {\left|{b}_a\right|}^2\right) $$ (2)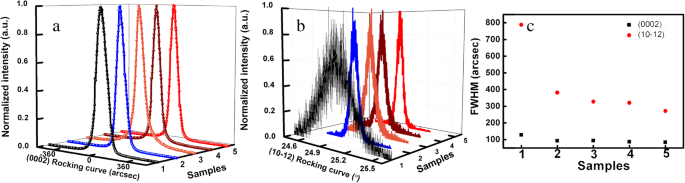
een Het (0002) vlak XRC van vijf AlN-monsters. b Het (10-12) vlak XRC van vijf AlN-monsters. c De FWHM van (0002, 10-12) vliegtuig XRC; de rode cirkel betekent de FWHM van het (10-12) vlak en het zwarte vierkant staat voor de FWHM van het (0002) vlak
waar ρ s en ρ e vertegenwoordigen de dichtheid van de dislocatie met respectievelijk schroef en randcomponent. β is de FWHM van XRC. |b c | komt overeen met c-axiale roosterconstante, en |b een | komt overeen met a-axiale roosterconstante van AlN. De FWHM van (0002) en (10-12) vlak XRC worden weergegeven in Fig. 1c voor de vijf AlN-monsters en de berekende TDD's van de vijf AlN-monsters worden weergegeven in Tabel 1.
De SE-experimentele gegevens van de vijf monsters zijn aangepast door CompleteEASE-software (J.A. Woollam Inc.) met behulp van een parametrisch halfgeleidermodel, dat de optische eigenschappen van directe bandgap-halfgeleiders effectief kan reproduceren [26]. Figuur 2a toont gedeeltelijke experimentele en passende curven van de vijf monsters. De gemiddelde kwadratische fout (MSE) van de vijf monsters is respectievelijk 8.139, 8.536, 9.175, 10.560 en 9.821, wat de goede resultaten bevestigt. Alle gegevens en aanpasresultaten staan in Aanvullend bestand 1.
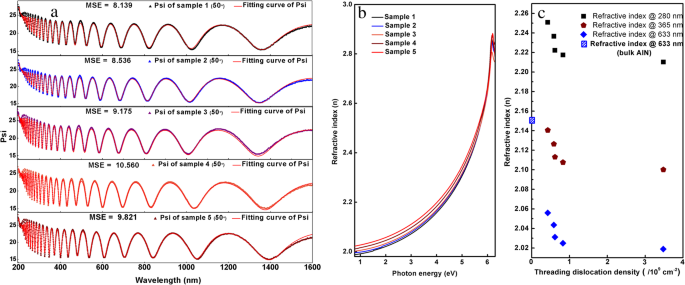
een Gedeeltelijke experimentele gegevens van SE-meting en aanpassingscurven. b De brekingsindexcurve. c Brekingsindex vs. verschillende TDD's bij 280 nm, 365 nm en 633 nm
De brekingsindexcurves van de vijf monsters kunnen worden verkregen uit aanpasresultaten zoals weergegeven in figuur 2b. Wanneer de fotonenergie lager is dan de bandgap van AlN (ongeveer 6,2 eV), neemt de brekingsindex toe met toenemende fotonenergie voor alle vijf monsters. Wanneer de fotonenergie echter hoger is dan 6,2 eV, neemt de brekingsindex af met de toename van de fotonenergie. Dit fenomeen kan worden beschreven door de Kramers-Krőnig-dispersierelatie. Met de afname van TDD's in AlN, neemt de brekingsindex toe van 2,019 tot 2,056 bij 633 nm, wat dichter bij die van bulk AlN ligt (2,15 bij 633 nm [27]). Het betekent dat de dislocaties in AlN de brekingsindex kleiner maken dan die van bulk AlN-kristal.
De relatie tussen de brekingsindex en TDD's bij 4,42 eV (280 nm, zonneblind UV), 3,40 eV (365 nm, bandgap van GaN) en 1,96 eV (633 nm) wordt getoond in Fig. 2c en in Tabel 1 Het is te zien dat de brekingsindex van AlN afneemt met de toename van TDD's. Met de toename van dislocatiedichtheden van 4,24 × 10 8 tot 3,48 × 10 9 cm − 2 , neemt de brekingsindex van AlN af van 2.2508 naar 2.2102 bij 280 nm.
Om het mechanisme te onthullen van hoe dislocaties de brekingsindex van AlN veranderen, wordt het door dislocaties veroorzaakte spanningsveld bestudeerd. De relatie tussen de brekingsindex en de ingediende rek wordt beschreven door formule (3) [28]:
$$ \Delta {\left(\frac{1}{n^2}\right)}_i=PS=\sum \limits_{ij}{p}_{ij}{s}_j $$ (3)In de formule, p ij zijn de elasto-optische tensor en S is de aanwezigheid van spanning. De matrix van foto-elastische constanten P van wurtziet AlN wordt weergegeven als uitdrukking (4) [29, 30].
$$ p=\left(\begin{array}{l}-0.1\kern1.75em -0.027\kern0.75em -0.019\kern1em 0\kern3em 0\kern2.75em 0\\ {}-0.027\kern0.5em -0.1\kern2em -0.019\kern1em 0\kern3em 0\kern2.75em 0\\ {}-0.019\kern0.5em -0.019\kern1em -0.107\kern1em 0\kern3em 0\kern2.75em 0\\ {}0\ kern2.75em 0\kern3em 0\kern3.5em -0.032\kern0.75em 0\kern2.75em 0\\ {}0\kern2.75em 0\kern3em 0\kern3.5em 0\kern3em -0.032\kern0.5em 0 \\ {}0\kern2.75em 0\kern3em 0\kern3.5em 0\kern3em 0\kern2.75em -0.037\end{array}\right) $$ (4)De spanningsveldmatrices van schroefdislocatie en randdislocatie in AlN worden beschouwd. De cilindrische ringmodellen van de twee soorten dislocaties worden beschreven in figuur 3. Volgens de modellen kan de verdeling van het rekveld rond een enkele dislocatie worden verkregen [31, 32].
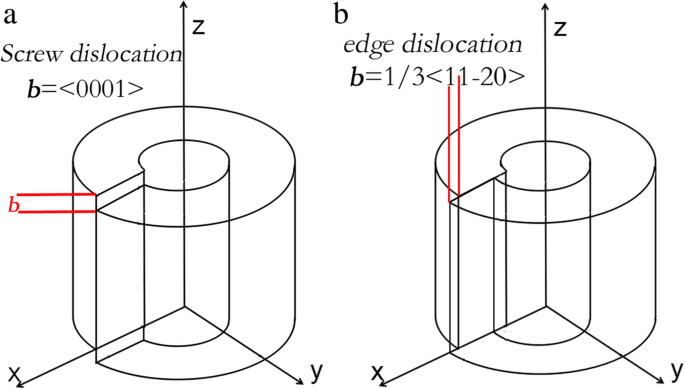
Cilindrisch ringmodel van a schroef dislocatie en b rand dislocatie
Het rekveld rond de dislocatie van de eenheidsschroef kan worden geschreven als:
$$ {e}_{xz}={e}_{zx}=-\frac{b}{4\pi}\frac{y}{\left({x}^2+{y}^2\ rechts)} $$ (5) $$ {e}_{yz}={e}_{zy}=\frac{b}{4\pi}\frac{x}{\left({x}^2 +{y}^2\right)} $$ (5a) $$ {e}_{xx}={e}_{yy}={e}_{zz}={e}_{xy}={ e}_{yx}=0 $$ (5b)Het rekveld rond de dislocatie van de eenheidsrand kan worden geschreven als:
$$ {e}_{xx}=-\frac{b}{4\pi \left(1-v\right)}\frac{y\left({x}^2-{y}^2\right )}{{\left({x}^2+{y}^2\right)}^2}-\frac{b}{2\pi}\frac{y}{\left({x}^2 +{y}^2\right)} $$ (6) $$ {e}_{yy}=\frac{b}{4\pi \left(1-v\right)}\frac{y\left (3{x}^2+{y}^2\right)}{{\left({x}^2+{y}^2\right)}^2}-\frac{b}{2\pi }\frac{y}{\left({x}^2+{y}^2\right)} $$ (6a) $$ {e}_{zz}=\frac{b\left(\lambda - 2 v\lambda -2 Gv\right)}{2\pi \left(2G+\lambda \right)\left(1-v\right)}\frac{y}{x^2+{y}^2} $$ (6b) $$ {e}_{xy}={e}_{yx}=\frac{b}{4\pi \left(1-v\right)}\frac{x\left({ x}^2-{y}^2\right)}{{\left({x}^2+{y}^2\right)}^2} $$ (6c) $$ {e}_{xz }={e}_{zx}={e}_{yz}={e}_{zy}=0 $$ (6d)waar b is de lengte van de Burgers-vector van eenheidsdislocatie en e vertegenwoordigt de spanning rond de dislocatie. G = 121 GPa is de afschuifmodulus van wurtziet AlN; λ = 117.1 GPa en v = 0,241 zijn respectievelijk de lame-constante en de Poisson-ratio [33, 34]. Volgens de correspondentie tussen e ij en S k (ik ,j = x ,j ,z; k =-1,2,3...6) [35], zetten we het rekveld om in matrixvorming zoals hieronder om de verandering van de brekingsindex, veroorzaakt door de dislocaties, verder weer te geven.
$$ {S}_{\mathrm{edge}}=\left({S}_1\kern0.5em {S}_2\kern0.5em {S}_3\kern0.5em 0\kern0.5em 0\kern0. 5em {S}_6\right) $$ (7) $$ {S}_{\mathrm{screw}}=\left(0\kern0.5em 0\kern0.5em 0\kern0.5em {S}_4\ {S}_5\kern0.5em 0\right) $$ (8)Als we de matrices (7) en (8) in formule (3) nemen, kunnen we de uitdrukking krijgen van Δn veroorzaakt door unitschroef en unitranddislocatie.
$$ \Delta {\left(\frac{1}{n^2}\right)}_{\mathrm{screw}}={\left(\frac{1}{n_1^2}-\frac{1 }{n_0^2}\right)}_{\mathrm{screw}}=-0.032\left({S}_4+{S}_5\right)=-0.008\frac{b\left(xy\right)} {\pi \left({x}^2+{y}^2\right)} $$ (9) $$ \Delta {\left(\frac{1}{n^2}\right)}_{ \mathrm{edge}}={\left(\frac{1}{n_1^2}-\frac{1}{n_0^2}\right)}_{\mathrm{edge}}=-0.146\left( {S}_1+{S}_2\right)-0.145{S}_3-0.037{S}_6=\hbox{-} 0.146\left(\frac{b}{4\pi \left(1-v\right) )}-\frac{b}{2\pi}\right)\frac{2y}{x^2+{y}^2}-0.145\frac{b\left(\lambda -2\lambda v-2 Gv\right)}{2\pi \left(2G+\lambda \right)\left(1-v\right)}\frac{y}{x^2+{y}^2}-0.037\frac{b }{4\pi \left(1-v\right)}\frac{x\left({x}^2-{y}^2\right)}{{\left({x}^2+{y }^2\rechts)}^2} $$ (10)Op basis van de berekening worden de verdelingen van de brekingsindex (neem de brekingsindex bij 633 nm als voorbeeld) rond eenheidsschroef en eenheidsranddislocaties getoond in Fig. 4. Het laat zien dat de brekingsindex rond de dislocatie verandert langs de radiale richting uit de dislocatiekern die als een inhomogeen medium kan worden beschouwd. Licht dat zich in AlN voortplant, zal dus overeenkomstig worden beïnvloed door TDD's. Verstrooiing en interferentie zullen optreden [36] wanneer licht door deze brekingsvelden rond dislocaties gaat. Als resultaat zal de brekingsindex van AlN veranderen, wat overeenkomt met de verstrooiingsmatrix van het inhomogene medium [37].
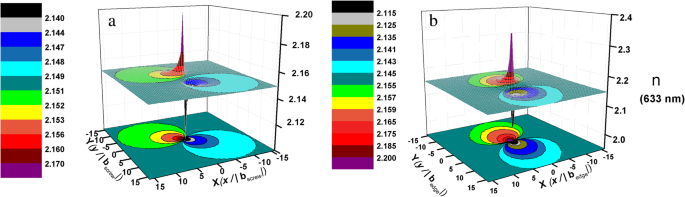
De verdeling van de brekingsindex bij 633 nm rond a eenheid schroef dislocatie en b eenheid rand dislocatie
Zoals vermeld in de sectie "Inleiding", moeten andere invloedsfactoren worden vermeden om te bewijzen dat de brekingsindex echt wordt beïnvloed door dislocaties. Alle monsters werden bij kamertemperatuur gemeten om de invloed van de temperatuur te vermijden. Om de invloed van de spanning in AlN-materiaal te ondervangen, werd het Raman-spectrum genomen om de spanning in AlN te bevestigen en de resultaten worden getoond in Fig. 5. De E g modus piek van saffier op 750 cm − 1 wordt genomen als kalibratie. De Raman-verschuivingspiek van AlN E 2 (h ) blauwverschuivingen met de afname van TDD's zoals weergegeven in tabel 1. De blauwverschuiving van E 2 (h ) piek betekent dat het AlN steeds meer drukspanning ondervindt van saffiersubstraat. Met de toename van de drukspanning komt de brekingsindex echter dichter bij die van bulk AlN bij 633 nm. Het kan duidelijk worden verkregen dat de spanning van AlN lijdt bij heterogene substraten weinig invloed heeft op de brekingsindex. Bijkomend bewijs om de conclusie te ondersteunen is dat de brekingsindex van AlN ook kleiner is dan die van bulk AlN wanneer AlN trekspanning ondervindt van het Si-substraat [38], wat hetzelfde is als de voorwaarde dat AlN in dit werk aan drukspanning lijdt. Dit fenomeen kan worden toegeschreven aan het feit dat de spanning van AlN onder substraten te klein is om een significante verandering aan te brengen in de brekingsindex van AlN. Als gevolg hiervan kan, vergeleken met de invloed van andere factoren, het effect van de spanning van substraten op de brekingsindex van AlN worden verwaarloosd.
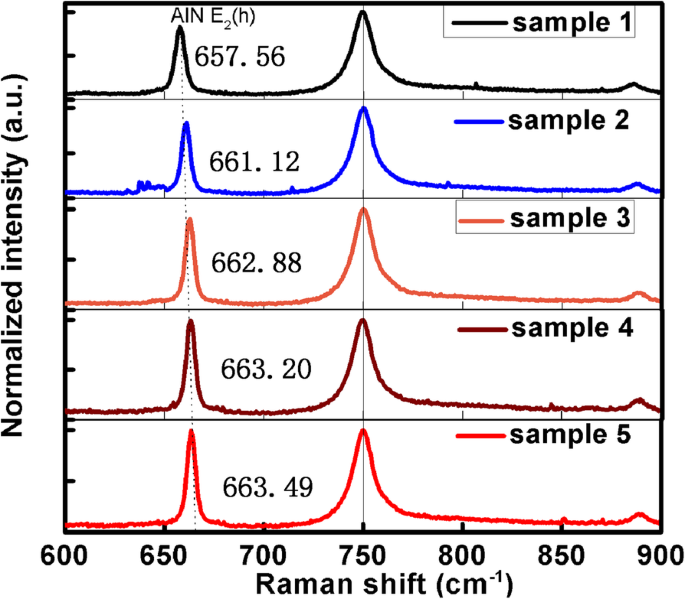
Raman-verschuivingsspectra van de vijf monsters
Hier wordt ook de bandgap van de vijf samples berekend. De optische absorptiecoëfficiënt α wordt geëxtraheerd uit SE-aanpassingsresultaten, en vervolgens de bandgap E g wordt berekend op basis van de onderstaande formule [39]:
$$ {\left(\alpha E\right)}^2=\left\{\begin{array}{c}C\left(E-{E}_g\right)\kern0.75em \left(E\ ge {E}_g\right)\\ {}0\kern4.75em \left(E<{E}_g\right)\end{array}\right. $$ (11)De plot van (αE ) 2 vs. E wordt weergegeven als Fig. 6. Het snijpunt van de x -as is de waarde van E g . Vanaf het snijpunt van passende curven op de x -as, wordt de toenemende bandgap van 6,1106 tot 6,1536 eV voor monster 1 tot monster 5 getoond in Fig. 6. De relatie tussen de brekingsindex en de bandgap wordt weergegeven zoals hieronder [16].
$$ n(E)={\left[a{\left(\frac{E}{E_g}\right)}^2\left(2-{\left(1+\frac{E}{E_g}\ rechts)}^{0.5}-{\left(1-\frac{E}{E_g}\right)}^{0.5}\right)+b\right]}^{0.5} $$ (12)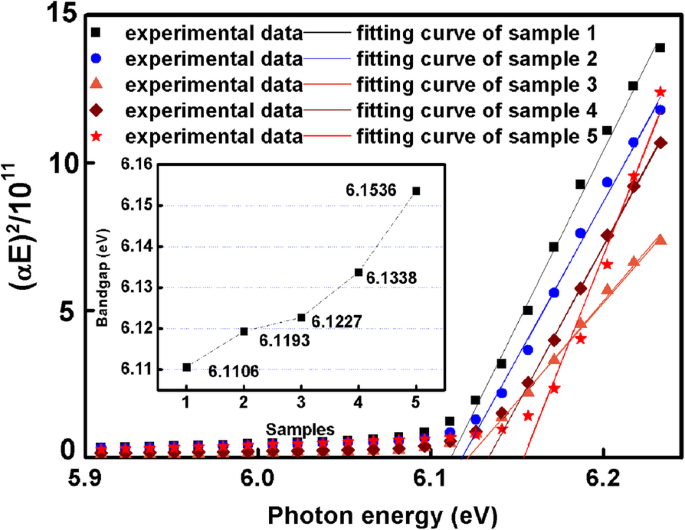
Afhankelijkheid van (αE ) 2 op (E ), toont de inzetafbeelding de bandgap van AlN-sjablonen
waar E is de fotonenergie en E g is de bandgap van AlN. een en b zijn constanten die gelijk zijn aan respectievelijk 13,70 en 7,81 voor AlN. De brekingsindex van AlN zou moeten afnemen met de toename van E g volgens de formule. In dit werk neemt de brekingsindex van AlN echter toe met de toename van E g , wat betekent dat de invloed van de bandgap op de brekingsindex van AlN kan worden verwaarloosd in vergelijking met de invloed van TDD's. Daarom speelt de verandering van TDD's een sleutelrol bij de verandering van de brekingsindex van AlN.
In combinatie met de bovenstaande analyses wordt bevestigd dat het spanningsveld op nanoschaal de verdeling van de brekingsindex rond dislocaties zal beïnvloeden, wat de brekingsindex van AlN verder zal beïnvloeden. De dislocaties zullen de breking van AlN verminderen volgens de experimentele gegevens.
Conclusies
Concluderend wordt het effect van TDD's op de brekingsindex van AlN zowel experimenteel als theoretisch bestudeerd. Door de invloed van temperatuur, spanning en bandgap te ondervangen, kan de conclusie worden getrokken dat de brekingsindex van AlN afneemt met de toename van TDD's. Verdere studies toonden aan dat het spanningsveld op nanoschaal rond dislocaties ertoe leidt dat de brekingsindex aanzienlijk verandert rond de dislocaties. Verstrooiing en interferentie zullen optreden zodra licht zich voortplant door dislocaties en dus zal de brekingsindex van AlN veranderen. De bevindingen in dit werk zullen gunstig zijn voor het optimaliseren van op AlN gebaseerde DUV-opto-elektronische apparaten.
Beschikbaarheid van gegevens en materialen
Alle gegevens kunnen op een passend verzoek worden verstrekt.
Afkortingen
- DBR:
-
Gedistribueerde Bragg-reflector
- DUV:
-
Diep ultraviolet
- EQE:
-
Externe kwantumefficiëntie
- FWHM:
-
Volledige breedte op halve maximum
- LED's:
-
Lichtgevende dioden
- LEE:
-
Efficiëntie van lichtextractie
- MOCVD:
-
Metaal-organische chemische dampafzetting
- MSE:
-
Gemiddelde kwadratische fout
- SE:
-
Spectroscopische ellipsometrische
- TDD's:
-
Dislocatiedichtheden inpassen
- XRC:
-
XRD schommelende curve
- XRD:
-
Röntgendiffractie
Nanomaterialen
- Invloed van molybdeen op de prestaties van roestvrij staal
- Gebruik van molybdeen in de medische sector
- Invloed van molybdeenelektroden op de kwaliteit van glasproducten
- Toepassingen van wolfraam op het gebied van legeringen
- Superprestaties van diamant op medisch gebied
- IBM-wetenschappers vinden een thermometer uit voor de nanoschaal
- De volgende gusher van Big Oil is op nanoschaal
- De nieuwe realiteit van verbonden buitendienst
- Op pad met IoT
- Machine learning in het veld
- De invloed van het materiaaltype op het ontwerp



