Verbeterd niet-lineair optisch effect in hybride vloeibaar-kristalcellen op basis van fotonisch kristal

Methoden

Materialen en voorbeelden

Structuur van de hybride LC-cellen wordt getoond in Fig. 1. De hybride cel heeft een sandwichachtig type, wordt gevormd door glas- en siliciumsubstraten en gevuld met nematische LC; de randen zijn gelijmd. De dikte van de nematische LC-laag is 20 m. Het vlakke glazen substraat is bedekt met ITO-elektrode. Het tweede substraat is gesneden uit een met fosfor gedoteerde siliciumwafel, de afmetingen zijn 17 × 17 mm ² . De soortelijke weerstand is 4,5 cm, de dikte is 380 m en de oriëntatie is 〈100〉. Het siliciumsubstraat bevat twee gebieden, namelijk een oppervlak met een periodiek microgestructureerd deel, dat in feite een fotonisch kristal is in het micrometerbereik, en een vlak deel van het oppervlak.

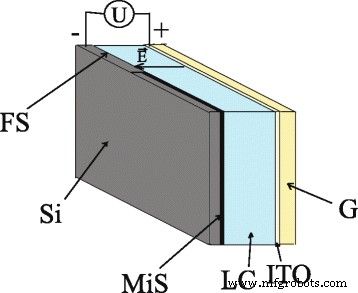
Structuur van een hybride LC-cel:siliciumsubstraat (Si ); microgestructureerd siliciumoppervlak (MiS ); plat siliconen oppervlak (FS ); vloeibare kristallen (LC ); glassubstraat (G ); ITO-elektrode (ITO ); aangelegde spanning (U ); elektrisch veld vector (\( \overrightarrow{E} \))

De drie Si-substraten, gebruikt in ons onderzoek, worden getoond in Fig. 2. De microstructuren vertegenwoordigen geëtste putjes die zijn gerangschikt in een vierkante matrix (de substraten 1 en 2) of in een driehoekige matrix (het substraat 3). De putten zijn vierkante micropiramides, die verschillen door de vorm, grootte en opstelling. Er zijn (1) regelmatige piramides, (2) afgeknotte piramides (kuilen) en (3) licht afgeknotte piramides. Normale micropiramides zijn 2 m hoog, dezelfde basiszijde van 2 m en een periodiciteit van 3 m. Putten hebben vergelijkbare parameters, maar ze zijn dicht op elkaar gepakt. Licht afgeknotte piramides hebben de basiszijde 1,5 m en periodiciteit 3,5 m. De microstructuren werden gevormd op de gepolijste kant van de siliciumwafel met standaard fotolithografische techniek, gevolgd door anisotroop etsen voor de substraten 1 en 3, of door plasma-etsen voor het substraat 2.

Afbeeldingen van microgestructureerd siliciumoppervlak gemaakt in optische microscoop. Micropiramides hebben de volgende vormen:regelmatige piramides (1), kuilen (2) en licht afgeknotte piramides (3)

Er werden twee nematische LC gebruikt:pure nematische 5CB (4×-(n -pentyl)-4-cyaanbifenyl) en nematisch mengsel E7. In alle gevallen is de moleculaire oriëntatie in een vloeibaar-kristallaag homeotroop en verschijnt deze spontaan op ITO- en siliciumoppervlakken waarbij de verwerkingstemperatuur niet hoger dan 50 °C wordt gehouden. We hebben vier monsters onderzocht, die verschillen door de vorm van de microstructuur en door de gebruikte LC. De monsters met siliciumsubstraten 1 en 2 bestaan ​​uit twee delen:een deel bevat een verkeerd gestructureerd oppervlak en het tweede deel is een vlak. In dergelijke monsters hebben we de mogelijkheid om de niet-lineaire respons in een platte cel (die een plat deel van het Si-substraat bevat) en in een microgestructureerde cel (die een microgestructureerd deel van het Si-substraat bevat) te vergelijken.

Op deze manier hebben we in onze experimenten de volgende hybride cellen:

1. 1)

   afgekort M1:glassubstraat + ITO/5CB/Si substraat 1, microgestructureerd oppervlak

2. 2)

   afgekort F1:glassubstraat + ITO/5CB/Si substraat 1, plat oppervlak

3. 3)

   afgekort M2:glassubstraat + ITO/5CB/Si substraat 2, microgestructureerd oppervlak

4. 4)

   afgekort F2:glassubstraat + ITO/5CB/Si-substraat 2, vlak oppervlak

5. 5)

   afgekort M3:glassubstraat + ITO/5CB/Si substraat 3, microgestructureerd oppervlak

6. 6)

   afgekort M4:glassubstraat + ITO/E7/Si substraat 3, microgestructureerd oppervlak

Experimentele opzet

Figuur 3 toont het schema van de experimentele opstelling, die is gebaseerd op de dynamische holografische methode met twee-golfmenging. Continue halfgeleider Nd:YAG-laser (frequentieverdubbeling, λ = 532 nm, P = 52 mW, single-mode generatie) is een lichtbron. Door middel van een bundelsplitser BS en een spiegel M wordt de laserstraling gesplitst in twee bundels B ₀ en B ₁ , convergerend op de cel onder een kleine hoek θ ≈ 0,01 rad. De invoerintensiteiten I ₀ en ik ₁ worden geëgaliseerd met behulp van het filter F1 en in ons geval I ₀ = Ik ₁ = 3.3 W/cm ² . De diameter van een laservlek op een cel is 1 mm.

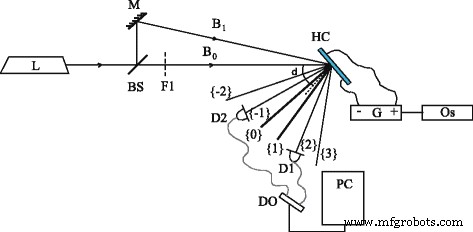
Schema van experimentele opstelling:laser (L ); spiegel (M ); bundelsplitser (BS ); optische filter (F1 ); balken (B ₀ ) en (B ₁ ); fotodiodes (D1 ) en (D2 ); hybride LC-cel (HC ); oscilloscoop (Os ); generator (G ); digitale oscillograaf (DO ); computer (PC ). De uitvoerdiffractieorders zijn {0} en {1} de hoofdorders; {−1} en {2} de eerste diffractieorders; {−2} en {3} de tweede diffractieorden. δ is de rotatiehoek van de cel

Twee laserstralen B ₀ en B ₁ vormen een interferentiepatroon in het monster. Beide invallende bundels hebben lineaire p polarisatie. Dus het interferentiepatroon voor intensiteitsmodulatie wordt gecreëerd. De normale LC-cel maakt de hoek δ met de bissectrice van B ₀ en B ₁ . Het elektrische DC-veld wordt aangelegd vanwege de bron G met de spanning U geregeld in het bereik van 0 tot 15 V. Het ITO-glassubstraat wordt ingesteld als de positieve elektrode. We hebben de intensiteiten van de eerste diffractie-orden {−1} en {2} gemeten met behulp van fotodiodes D1 en D2 via computergestuurde digitale oscilloscoop DO. De hoeken van celrotatie werden aangepast om het diffractiesignaal te maximaliseren en leken δ . te zijn ≈ 40 − 55 ⁰ voor verschillende monsters. Deze resultaten vallen samen met de experimenten van andere groepen (bijvoorbeeld [9, 12]); de reden voor een dergelijk effect valt buiten het bestek van ons onderzoek.

Model van zelfdiffractie van golven in Raman-Nath-benadering

Zelfdiffractie van golven is in verschillende werken overwogen [17, 18]. Wanneer de zelfdiffractie van twee ingangsgolven op het fotogeïnduceerde dunne brekingsindexrooster plaatsvindt, verschijnen er veel diffractieorden aan de uitgang. Door de intensiteiten in de eerste diffractieorden te meten, kan men de modulatiediepte van het rooster berekenen (Δn ). Omdat in het Kerr-achtige medium de voorwaarde Δn = n ₂ Ik ₀ is geldig (waar I ₀ is de intensiteit van de opwindende bundel), de coëfficiënt van de niet-lineaire breking n ₂ is mogelijk om te berekenen.

In deze sectie zoeken we naar de oplossing voor de diffractie-efficiëntie van de eerste diffractieorden in het geval van niet-verschoven sinusoïdaal brekingsindexrooster. Dan zijn de intensiteiten in symmetrische orden gelijk. De modellering gaat uit van de golfvergelijking, waarin zowel het elektrische veld \( \overrightarrow{E} \) als het gemoduleerde deel van de diëlektrische permittiviteit Δε als gevolg van het Kerr-achtige niet-lineaire effect hangt af van de coördinaat z (langs de golfvoortplanting):

waar c is de lichtsnelheid in het vacuüm, \( {\varepsilon}_0={n}_0^2 \) staat voor de diëlektrische permittiviteit van een medium en n ₀ is de brekingsindex. We zoeken de oplossing van de golfvergelijking (1) in de som van alle diffractieorden, dit zijn vlakke golven gepolariseerd in de richting van de as \( \overrightarrow{y} \):

waar ω ₀ is de frequentie van de laserstraling, \( \overrightarrow{r} \) is de coördinaat, en “c. c .” geeft de complexe geconjugeerde term aan. In onze weergave is het handig om de verzwakkingscoëfficiënt uit te drukken als α = α _buikspieren + α _sc , die rekening houdt met de verliezen van laserstraling zowel bij absorptie α _buikspieren en verstrooiing α _s . Figuur 4 toont het golf-vectordiagram van zelfdiffractie in Raman-Nath-benadering. Het laat zien dat de golf van de m -de diffractieorde komt overeen met de ruimtelijke richting beschreven door de golfvector \( {\overrightarrow{k}}_m \). Diffractie-orders m = 0 en m = 1 hoort bij twee opwindende stralen B ₀ en B ₁ . De golfvector van de m -de diffractieorde is \( {\overrightarrow{k}}_m={\overrightarrow{k}}_0- m\overrightarrow{K} \), en \( \overrightarrow{K} \) is de golfvector van het fotogeïnduceerde rooster. De permittiviteitsmodulatie Δε wordt gedefinieerd in de vorm van een rooster:

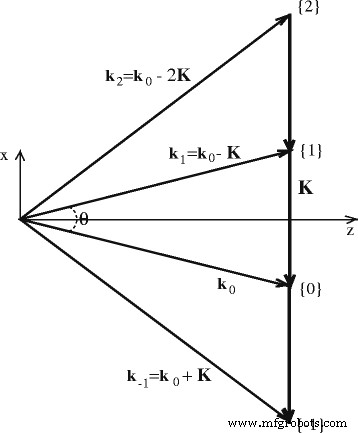
Golfvectordiagram van zelfdiffractie van twee coherente golven (beschreven door \( {\overrightarrow{k}}_0 \) en \( {\overrightarrow{k}}_1 \)) in de Raman-Nath-benadering

Door oplossing (2) en (3) in Vgl. (1), verkrijgt men de relatie voor een langzame variabele amplitude A _m van de m -de volgorde:

$$ \frac{\partial {A}_m}{\partial z}+ i\frac{\left({k}_0^2-{k}_m^2\right)}{2{k}_{mz }}{A}_m-\frac{1}{2}\alpha \cdot {A}_m=- i\frac{k_{\upsilon}^2}{4{k}_{mz}}\left[ {\varepsilon}_1{A}_{m+1}+{\varepsilon}_1^{*}{A}_{m-1}\right] $$ (4)

waar k _υ = 2π /λ is de golfvector in het vacuüm, en het teken "∗" geeft de complexe vervoeging aan. Omdat in onze weergave de belangrijkste opnamebundels van de orden m = 0 en m = 1 identiek zijn aan de invoer, evenals over de dikte van het monster, volgt hieruit dat ε ₁ is een reële waarde en is niet afhankelijk van de coördinaat z (zie [18]):\( {\varepsilon}_1(t)={\varepsilon}_1^{*}(t) \). Voor verdere transformatie van Vgl. (4) introduceren we een nieuwe functie \( {U}_m\left( z, t\right)={A}_m\left( z, t\right) \exp \left(-\frac{1}{ 2}\alpha z\right) \exp \left( im\frac{\pi}{2}\right) \), geef T aan = exp(−αz ) de verliezen van de lichtintensiteit in het medium, en definieer \( {\varepsilon}_1=T{\tilde{\varepsilon}}_1 \). Door een nieuwe variabele te introduceren \( \tilde{z}={k}_{\upsilon}/\left({n}_0 \cos \left(\theta /2\right)\right)\cdot \left(1 - T\right)/\left(2\alpha \right) \), waarbij θ is de convergerende hoek, Vgl. (4) kan worden geschreven als:

$$ 2\frac{\partial {U}_m}{\partial \tilde{z}}={\tilde{\varepsilon}}_1\left[-{U}_{m+1}+{U}_ {m-1}- i\frac{2 m\left( m-1\right)}{\phi}{U}_m\right] $$ (5)

waarbij parameter ϕ wordt gedefinieerd door \( \phi =T{\tilde{\varepsilon}}_1/\left(2{n}_0^2{ \sin}^2\left(\theta /2\right)\right) \) .

In de voorwaarden van de Raman-Nath-benadering is het mogelijk om de laatste term aan de rechterkant van de vergelijking te verwaarlozen. (5) (Ref. [18]), d.w.z. 2m (m − 1)/ϕ < < 1 voor elke m . Door vervolgens een nieuwe variabele \( \zeta =\tilde{z}{\tilde{\varepsilon}}_1(t) \) te introduceren, verkrijgen we onze hoofdvergelijking in de Raman-Nath-benadering:

$$ 2\frac{\partial {U}_m\left(\zeta, t\right)}{\partial \zeta}+{U}_{m+1}\left(\zeta, t\right)- {U}_{m-1}\left(\zeta, t\right)=0 $$ (6)

Deze relatie is formeel een bekende representatie voor de Bessel-functie, dus de oplossing kan worden uitgedrukt door middel van Bessel-functies in de vorm:

$$ {U}_m\left(\zeta, t\right)={\displaystyle \sum_{n=0}^{\infty }{C}_n^m(t){J}_n\left(\zeta \rechts)} $$ (7)

De vergelijking (6) voldoet aan de symmetrie-eigenschappen \( {U}_0{U}_0^{*}={U}_1{U}_1^{*} \) voor het paar hoofdliggers, evenals voor alle paren van de afgebogen bundels (\( {U}_2{U}_2^{*}={U}_{-1}{U}_{-1}^{*} \)). Merk op dat bij z = 0, E ₀ (0, t ) = E ₁ (0, t ) ≠ 0, maar E _m (0, t ) = 0 voor m ≠ 0, 1 en vervolgens uitvoerintensiteiten van de eerste diffractieorden I _{−1} (d ,t ) en ik _{2} (d ,t ) is gelijk en wordt gedefinieerd door een formule (zie ook [18]):

$$ {I}_{\left\{-1\right\}}\left( d, t\right)={I}_{\left\{2\right\}}\left( d, t\ rechts)=T{I}_0\left(0, t\right)\left[{J}_1^2\left(\zeta \right)+{J}_2^2\left(\zeta \right)\ rechts] $$ (8)

waar d is de dikte van een niet-lineair medium; Ik ₀ is de intensiteit van een laserstraal; J ₁ en J ₂ zijn de Bessel-functies van de eerste soort van respectievelijk de eerste en tweede orde. Omdat in ons geval de intensiteiten I ₀ en ik ₁ gelijk zijn, d.w.z. 2I ₀ = Ik _laser , bijgevolg de waarde van ζ kan worden geschreven als:

$$ \zeta =\tilde{z}{\tilde{\varepsilon}}_1=\frac{k_{\upsilon}}{n_0\cdot \cos \left(\theta /2\right)}\frac{1 - T}{2\alpha}{\tilde{\varepsilon}}_1\circa \frac{k_0}{n_0}\frac{1- T}{2\alpha}2{n}_0\varDelta n $$ ( 9)

In een Kerr-achtig medium Δn = n ₂ Ik ₀ , waar n ₂ vertegenwoordigt de niet-lineaire brekingscoëfficiënt, dan de uiteindelijke waarde van ζ heeft een eenvoudigere vorm:

$$ \zeta =\frac{2\pi}{\lambda}\frac{1- T}{\alpha}{n}_2{I}_0 $$ (10)

De diffractie-efficiëntie η van de eerste diffractieorde wordt bepaald als η = Ik _{−1} /(TI ₀ ). Aan de andere kant kan de diffractie-efficiëntie experimenteel worden verkregen door de intensiteit I . te meten _{−1} en de transmissiecoëfficiënt van een cel T . De algemene formule (8) is geldig om de diffractie-efficiëntie in een groot bereik te berekenen. Voor kleinere diffractie-efficiënties, η ≤ 2%, de goede benadering is alleen de eerste polynoomterm van (8):η ≈ ζ ² /4. Bijgevolg kan men een eenvoudige relatie verkrijgen voor n ₂ :

$$ {n}_2=\frac{\lambda}{\pi}\frac{\alpha}{1- T}\frac{\sqrt{\eta}}{I_0} $$ (11)

Opgemerkt moet worden dat de afgeleide Vgl. (11) heeft dezelfde vorm als de vergelijking die conventioneel wordt verkregen voor het geval van de diffractie van slechts één sondebundel van een gegeven brekingsindexrooster (zie bijvoorbeeld Ref. [19]). Maar voor grote waarden van η , dat gebruikelijk is voor LC-cellen, moeten nauwkeurigere relaties (8) en (10) worden gebruikt om de waarden te berekenen ζ en n ₂ .

De waarde kennen n ₂ , kan men de niet-lineaire gevoeligheid van het medium definiëren met behulp van de uitdrukking:

$$ {\chi}^{(3)}\left[\mathrm{esu}\right]={n}_2\left[\frac{\mathrm{c}{\mathrm{m}}^2}{ W}\right]\cdot \frac{9\cdot {10}^4}{4\pi} c\cdot {\varepsilon}_e\cdot {n}_0^2 $$ (12)

waar ε _e is de elektrische constante. In het geval van nematisch 5CB gebruiken we de brekingsindex voor de homeotrope oriëntatie van moleculen n ₀ = n _⊥ = 1,51 als die van de gewone brekingsindex; evenzo voor nematisch mengsel E7, n ₀ = n _⊥ = 1.5268.

De ontwikkelde theoretische benadering is geldig voor dunne films die Kerr-achtige optische niet-lineariteit bezitten, wanneer de lichtverliezen op zowel de absorptie als de verstrooiing groot zijn. Omdat voor de zelfdiffractiemethode geen extra laserbron als sonde nodig is, wordt het mengen met twee golven een eenvoudige methode voor de diagnostiek van optische niet-lineariteit van dunne media, inclusief LC-cellen.

Resultaten en discussies

We suggereren dat het niet-lineaire optische mechanisme in hybride LC-cellen een oppervlakte-geïnduceerd fotorefractief effect is, dat de oriëntatie van de LC-moleculen verandert in de bulk die vanaf het oppervlak wordt geïnitieerd [12, 13]. In de twee-golf mengexperimenten wordt het monster verlicht door een periodiek lichtinterferentiepatroon gevormd door twee coherente laserstralen. Dit patroon creëert een ruimtelijke ladingsmodulatie op de LC-substraatinterface. Resulterende periodieke distributie van het elektrische veld op het oppervlak stimuleert modulatie van de richting van de regisseur op het substraat. De heroriëntatie van de moleculen begint aan het oppervlak en verspreidt zich naar LC-volume.

Typische twee-golf experimentele mengprestaties met hybride LC-cellen worden getoond in Fig. 5. Bij afwezigheid van een elektrisch veld nemen we een regelmatige tweedimensionale structuur waar van de belangrijkste laserstralen die worden gereflecteerd door een microgestructureerd substraat van de cel (Fig. 5a). ). Na het aanleggen van gelijkspanning verschijnen er veel diffractie-orders naast elk paar hoofdstralen als gevolg van excitatie van het brekingsindexrooster in de cel (figuur 5b). In het geval van platte cellen F1 en F2 is er geen multi-verstrooiingspatroon, we observeren slechts één middellijn na het aanleggen van de spanning. We maten de intensiteiten in de eerste diffractie-orden {−1} en {+2} in de middenlijn in de stabiele toestand voor alle cellen:platte cellen en cellen met een microgestructureerd oppervlak. Vervolgens hebben we de diffractie-efficiëntie berekend volgens η = Ī _{−1} /(TI ₀ ), waar Ī _{−1} is de gemiddelde intensiteit van twee eerste diffractieorden (Ī _{−1} = (Ik _{−1} + Ik _{2} )/2) en T is de transmissiecoëfficiënt van de cel.

Typische patronen van verstrooiing voor twee interfererende laserstralen gevormd door hybride niet-lineaire LC-cel met microgestructureerd oppervlak. een Verstrooiingspatroon van een hybride cel zonder aangelegd elektrisch veld. b Vorming van veel diffractie-orden (de Raman-Nath-zelfdiffractie) bij het aanleggen van elektrische gelijkspanning. De middellijn wordt weergegeven in (b ) door een stippellijn

Merk op dat het oppervlakte-geïnduceerde fotorefractieve effect, benut in onze experimenten, sterk afhangt van de rotatiehoek van het monster ten opzichte van de bissectrice van de convergentiehoek tussen twee ingangsgolven (zie bijvoorbeeld [9, 12, 13]). Dus met de normale positie van het monster, wanneer de plaat van het monster loodrecht op de bissectrice van de golven staat, worden geen diffractie-orders waargenomen. Tegelijkertijd lijkt in ons geval, wanneer het monster wordt geroteerd ten opzichte van deze bissectrice, het foto-geïnduceerde brekingsindexrooster verschoven te zijn ten opzichte van het lichtinterferentiepatroon. Dit effect zou zich moeten manifesteren in het bestaan ​​van energieoverdracht tussen diffractieorden. In het geval van onze hybride cellen en twee laserstralen met gelijke ingangsintensiteiten, hebben we waargenomen dat het verschil van de intensiteiten in de eerste diffractieorden niet groter is dan 10%. We hebben een gemiddelde waarde tussen deze twee gemeten intensiteiten genomen die wordt gebruikt voor verdere berekeningen van de coëfficiënt van de niet-lineaire breking. Deze waarde behoort tot het nauwkeurigheidsbereik van onze schattingen van de niet-lineaire optische coëfficiënten. Merk ook op dat het ontwikkelde wiskundige model is teruggebracht tot een vrij eenvoudige resulterende formule en niet de veranderingen van golffasen in een volume van een niet-lineaire laag omvat. Het effect van niet-lokale respons in het medium en de energieoverdracht tussen golven zal in onze volgende werken zorgvuldig worden overwogen.

In tabel 1 verzamelen we experimentele parameters gemeten voor de hybride LC-cellen. De transmissiecoëfficiënt wordt gedefinieerd als T = Ik ^uit /Ik ₀ , waar ik ₀ is de intensiteit van een enkele invallende straal, en I ^uit is de intensiteit van de uitgangsstraal. T bestaat uit twee delen:T = R _s T _een , waar R _s houdt rekening met het intensiteitsverlies voor verstrooiing van het microgestructureerde oppervlak om een ​​periodiek lichtpatroon te vormen; en T _een = exp(−αd _eff ) beschrijft intensiteitsverlies bij absorptie tijdens lichtvoortplanting in een bulk van LC-cellen. In Tabel 1 presenteren we ook de waarden d _eff , wat een effectieve dikte is voor een zich voortplantende bundel in een cel. Merk op dat we in onze metingen de verliezen op lichtreflectie van de ingangsglasgrens van een cel verwaarlozen.

Gemeten diffractie-efficiëntie voor alle cellen, afhankelijk van de aangelegde spanning, wordt getoond in Fig. 6. Men kan zien dat de diffractie-efficiëntie zijn maximum bereikt voor een bepaalde spanning, die in verschillende cellen verschilt; deze spanning is hoger voor microgestructureerde cellen in vergelijking met platte (vergelijk F1 en M1, F2 en M2); evenals deze spanning wordt veranderd in afhankelijkheid van een vorm van de microstructuur (vergelijk M1, M2, M3, M4). We benadrukken ook dat de diffractie-efficiëntie vrij grote waarden bereikt in LC-cellen (tot 9% voor de cellen M1 en F1). We gebruiken meetwaarden van η om niet-lineaire optische kenmerken van onderzochte LC-cellen te berekenen, namelijk de niet-lineaire brekingscoëfficiënt n ₂ en effectieve niet-lineaire gevoeligheid χ ⁽³⁾ , rekening houdend met het feit dat de LC-cellen Kerr-achtige optische niet-lineariteit bezitten.

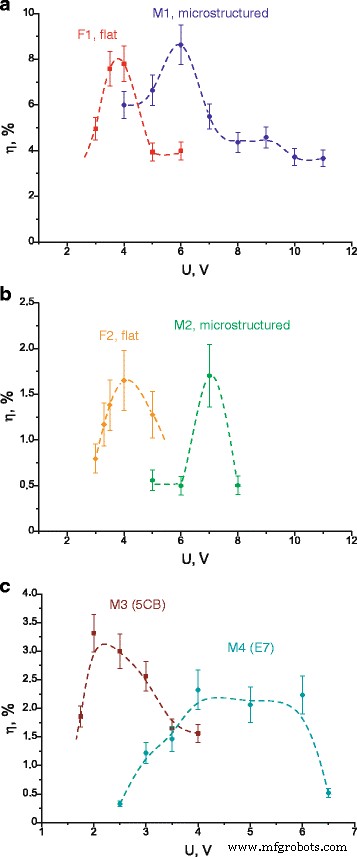
Diffractie-efficiëntie van de eerste diffractie-orde in afhankelijkheid van aangelegde spanning. een Cellen M1 en F1. b Cellen M2 en F2. c Cellen M3 en M4. Stippellijnen alleen gepresenteerd voor de visualisatie

Coëfficiënten van niet-lineaire breking berekend uit experimentele metingen van de diffractie-efficiëntie worden getoond in Fig. 7 voor alle cellen. In het geval van cellen M1 en F1 evenals M3 en M4, n ₂ wordt berekend aan de hand van de hoofdformules (8) en (10) als de gemeten diffractie-efficiënties η> 3,5%. We gebruiken de benaderende formule (12) voor de cellen M2 en F2, als de verkregen η < 2%. We verkrijgen dat de maximale coëfficiënt van niet-lineaire breking hoger is in een cel met een microgestructureerd substraat in vergelijking met platte cellen (zie Fig. 7a, b). Tabel 2 toont de waarden van niet-lineaire gevoeligheid berekend op basis van de maximale waarden van n ₂ in Fig. 7. Niet-lineaire gevoeligheid bleek in wezen verbeterd (met 30-100%) in de cellen met microgestructureerd substraat met betrekking tot de cellen gemaakt van platte substraten. Redenen die leiden tot toenemende modulatiediepte van het dynamische rooster in de cellen die microgestructureerde substraten bevatten, zijn onderwerp van verder onderzoek. We veronderstellen dat dit effect verband houdt met de initiële heroriëntatie van moleculen die ontstaan ​​op een microgestructureerd oppervlak.

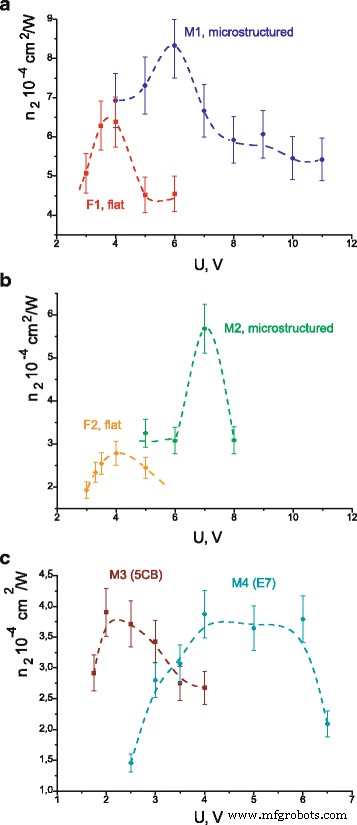
Berekende coëfficiënten van niet-lineaire breking in afhankelijkheid van aangelegde spanning voor cellen M1 en F1 (a ); M2 en F2 (b ); M3 en M4 (c ). Stippellijnen are for the visualisation only

Conclusies

We have investigated the nonlinear optical effect in novel hybrid LC cells based on a silicon photonic crystal. The cell consists of two different materials separated by a thin LC layer with homeotropic orientation of molecules. One material is a glass substrate with ITO electrode. The second one is silicon substrate with periodic microstructured surface. Microstructures in a shape of periodically arranged micro-pyramids are etched on the silicon surface by applying the chemical photolithography method or plasma etching one.

We apply the dynamic holography method with two-wave mixing to define the efficiency of self-diffraction of the dynamic grating induced in LC layer. A theoretical model for the Raman-Nath self-diffraction, offered for calculating the diffraction efficiency in the first diffraction orders, have allowed us to determine the nonlinear refraction coefficient n ₂ , and nonlinear susceptilibity χ ⁽³⁾ of the cells. We have also made a comparative analyses of nonlinear parameters obtained for cells with and without microstructures. Nonlinear susceptibility appeared to be essentially enhanced (by 30 − 100%) in the microstructured cells with respect to the cells made of flat surfaces. The underlying mechanism of the optical nonlinearity is the surface-induced photorefractive effect in the pure nematic LC. The increased modulation depth of the refractive index might be connected with initial reorientation of the molecules arising on the microstructured substrate.

The developed theoretical approach could be valid for determination of nonlinear optical characteristics of thin films possessing Kerr-like optical nonlinearity, in which the losses on the both absorption and scattering are large, as well as in the either transmission or reflection geometries. Photorefractive hybrid LC cells are perspective as new samples of electro-optical microsystems, including multi-channel SLMs. Additionally, two-wave mixing technique in such nonlinear cells may be successfully implemented in multi-channel couplers, switches, and optical communication lines. They may be also applied in networks, if to ensure the independent control of each channel in LCD structures.

Afkortingen

5CB:

4′-(n -pentyl)-4-cyanobiphenyl

E7:

Liquid crystal mixture

F1:

Hybrid LC cell, composed by flat part of Si plate 1/5CB/glass plate covered by ITO

F2:

Hybrid LC cell, composed by flat part of Si plate 2/5CB/glass plate covered by ITO

ITO:

Conductive layer of indium-tin-oxide

LC:

Liquid crystals

M1:

Hybrid LC cell, composed by microstructured part of Si plate 1/5CB/glass plate covered by ITO

M2:

Hybrid LC cell, composed by microstructured part of Si plate 2/5CB/glass plate covered by ITO

M3:

Hybrid LC cell, composed by microstructured part of Si plate 3/5CB/glass plate covered by ITO

M4:

Hybrid LC cell, composed by microstructured part of Si plate 4/E7/glass plate covered by ITO

Si:

Silicon