Impact van oppervlaktetoestanden en aluminiummolfractie op oppervlaktepotentiaal en 2DEG in AlGaN/GaN HEMT's

Abstract

De aanwezigheid van oppervlaktevallen is een belangrijk fenomeen in AlGaN/GaN HEMT. De elektrische en fysische eigenschappen van deze oppervlaktevallen zijn geanalyseerd door de studie van de 2DEG-elektronenconcentratie samen met de variatie van het aluminiumpercentage in de barrièrelaag van HEMT. Deze analyse laat zien dat van diepe naar ondiepe donoren de procentuele verandering in elektronendichtheid in 2DEG verzadigd raakt (bijna 8%) met verandering in aluminiumconcentratie. De diepte van de kwantumpotentiaal ver onder het Fermi-niveau wordt ook geanalyseerd en blijkt verzadigd te raken (bijna 2%) met aluminiumpercentage wanneer de energie van de oppervlaktedonor verandert van ondiep naar diep. De fysica achter dit collectieve effect wordt ook geanalyseerd via een banddiagram. Het effect van oppervlaktedonorvallen op het oppervlaktepotentieel is ook in detail besproken. Deze oppervlaktetoestanden worden gemodelleerd als donortoestanden. Diepe donor (E _C − E _D = 1.4 eV) naar ondiepe donor (E _C − E _D = 0,2 eV) oppervlaktevallen worden grondig bestudeerd voor de donorconcentratie van 10¹¹ tot 10¹⁶ cm⁻² . Dit onderzoek betreft een variatie in de aluminiumconcentratie van 5 tot 50%. Dit artikel presenteert voor het eerst de uitgebreide TCAD-studie van oppervlaktedonor en analyse van elektronenconcentratie in het kanaal en 2DEG-vorming op het AlGaN-GaN-interface.

Inleiding

Hoogfrequente en krachtige toepassingen zijn de twee belangrijkste kenmerken van het GaN-materiaal die in de afgelopen drie decennia zijn bestudeerd [1, 2]. Een van de belangrijkste voordelen van de AlGaN/GaN-structuur is de vorming van 2DEG in de driehoekige potentiaalput op het AlGaN-GaN-interface, zelfs zonder opzettelijke dotering in de barrièrelaag [3, 4]. Het is goed bewezen dat spontane en piëzo-elektrische polarisatie bestaat in de AlGaN-laag van de AlGaN/GaN-structuur [3]. Deze polarisatie resulteert in twee tegenover elkaar liggende ladingen aan de onder- en bovenkant van de AlGaN-barrièrelaag. Deze ladingen van het polarisatieblad alleen zijn niet voldoende om een driehoekige potentiaalput te vormen op het AlGaN-GaN-interface. Om dit aan te pakken, Ibbetson et al.. [5] suggereerde dat er een positieve ladingslaag zou moeten zijn aan het oppervlak van de AlGaN-laag. Deze positieve ladingen verschijnen als gevolg van de ionisatie van de oppervlaktedonortoestanden (1,42 eV van geleidingsband met 1,35 × 10¹³ cm⁻² ) aan de oppervlakte [6].

Vetury et al. [7] onderzocht het effect van deze oppervlaktetoestanden met behulp van potentiële sondes als drijvende poort. Het effect van oppervlaktetoestanden op DC- en RF-prestaties van AlGaN/GaN HEMT is onderzocht [8, 9]. Schottky-poortgedrag op nanometerschaal bespreekt de virtuele poortvorming in het niet-gated gebied als gevolg van oppervlaktedonortoestanden [10]. De vaste oppervlaktedonorstatussen worden gebruikt om het zelfverhittingseffect in HEMT [11] te analyseren. Longobardi et al. [12] voerde de eerste TCAD-simulatie uit om het effect van oppervlaktedonortoestanden op de DC-kenmerken van AlGaN/GaN MISFET's te bestuderen. Om deze oppervlaktedonortoestanden in de TCAD-simulatie te activeren, introduceerden Bakeroot en anderen een ander model [13, 14]. Afvoer-/bronweerstanden zijn ook afhankelijk van poortvoorspanning vanwege de vorming van de virtuele poort in het niet-gepoorte gebied van het AlGaN-oppervlak. Pradeep et al. [15] hebben de extractieprocedure voor mobiliteit en weerstand ontwikkeld op basis van lineaire DC-karakteristieken van AlGaN/GaN HEMT. Meneghesso et al.. [16] besprak de oppervlaktetoestand als een val die de zeer dichte gatenlaag op het oppervlak van AlGaN vangt om elektronen in 2DEG te compenseren. De oppervlaktedonorvallen die beschikbaar zijn aan de bovenkant van de AlGaN-laag veranderen het elektrische gedrag van het apparaat wanneer deze vallen worden bezet door elektronen met een negatieve gate-bias [17]. De relatie tussen oppervlaktedonorvallen en 2DEG-elektronen is ook besproken door middel van TCAD-simulatie door gebruik te maken van tijdsafhankelijke transportfenomenen [18]. Hoewel verschillende karakteriseringstechnieken zijn onderzocht, hebben Tapajna et al. [19] gebruikte een drempelwaarde-transiënte methode om de interface-acceptorvallen te onderzoeken, maar de karakterisering van de oppervlaktedonorvallen is nog onontgonnen. Een uitgebreide computationele modelleringsaanpak voor de oppervlakteval als donor is ook besproken [20]. Gucmann et al. [21] besprak dat als de dichtheid van de oppervlaktedonor groter is dan de polarisatieladingconcentratie, het elektron wordt overgebracht naar het AlGaN-GaN-interface om de 2DEG in het kanaal te laten ontstaan.

De hierboven besproken literatuur heeft zoveel relevante aspecten van de AlGaN/GaN-heterostructuur gerapporteerd, maar houdt geen rekening met het gecombineerde effect van de oppervlaktedonor (concentratie + energie) en de bijdrage van aluminiumconcentratie aan de tweedimensionale elektronenconcentratie. Het is duidelijk dat het aluminiumpercentage primair verantwoordelijk is voor de polarisatielading in de AlGaN-barrièrelaag [3].

Om een passend fysiek begrip van een dergelijk effect te geven, hebben we het volgende onderzoek in het huidige werk behandeld (i) het effect op tweedimensionale elektronenconcentratie met veranderingen in de oppervlaktedonorval van diep naar ondiep, samen met aluminiumpercentageveranderingen in AlGaN-barrièrelaag, (ii) het effect van oppervlakteval en aluminiumpercentage op oppervlaktepotentiaal en (iii) de invloed van oppervlaktedonorvanger en aluminiumpercentage op de driehoekige potentiaalput op het AlGaN-GaN-interface.

Methodesectie en simulatie instellen

2D-apparaatsimulaties werden uitgevoerd met behulp van Synopsys's Sentaurus TCAD-versie L-2016.12 [22]. We hebben de TCAD-simulatie-opstelling gekalibreerd door het experimentele resultaat van de AlGaN/GaN HEMT-heterostructuur [15] te reproduceren, zoals weergegeven in figuur 1b.

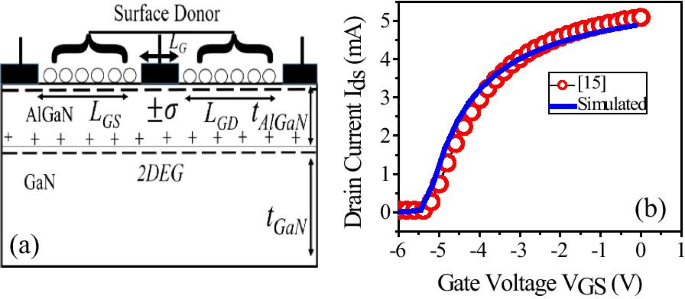
een Schema van 2D gesimuleerde structuur met Al-molfractie van 28%. b Kalibratie van de simulatie-opstelling door de gerapporteerde experimentele resultaten te reproduceren [15]

Het gekalibreerde apparaat heeft een AlGaN-barrièrelaag van 30 nm bovenop de GaN-bufferlaag van 2 μm. Schottky-poortlengte (L _G ) van 1 m wordt symmetrisch bovenop de AlGaN-barrièrelaag geplaatst. Niet-gated gebied van poort tot afvoer/bron (L _GD /L _GS ) heeft een afmeting van elk 2,5 m en de breedte van het apparaat is 150 μm.

Het simulatieplatform pakt drie condities aan (Poisson-conditie naast elektronen- en gatcontinuïteitsconditie) die toezicht houdt op het halfgeleidergedrag.

Het zelfconsistente drift- en diffusie (DD) transportmodel is ook inbegrepen. Lombardi-mobiliteit en het verenigde mobiliteitsmodel van Philip werden ingeroepen om de mobiliteitsdegradatie als gevolg van het elektrische veld en doping te vergemakkelijken. Bovendien werd het Auger- en SRH-recombinatiemodel (Shockley-Read-Hall) gebruikt samen met Fermi-Dirac-statistieken. Het Slotboom-model wordt geactiveerd om de bandgap-vernauwing van zwaar gedoteerde afvoer- en brongebied tegen te gaan. Aangezien deze structuur twee lagen heeft en we het aluminiumpercentage in de AlGaN-barrièrelaag veranderen, wordt de polarisatielading geïntroduceerd volgens de vergelijking van [3]:

$$\links| {\sigma (x)} \rechts| =\links| {2\frac{a(0) - a(x)}{{a(x)}}\left\{ {e_{31} (x) - e_{33} \frac{{C_{13} (x )}}{{C_{33} (x)}}} \right\} + P_{{{\text{SP}}}} (x) - P_{{{\text{SP}}}} (0 )} \rechts|$$ (1)

waar P _SP is spontane polarisatie, e ₃₃ en e ₃₁ zijn piëzo-elektrische coëfficiënten, C ₃₃ en C ₃₁ zijn elastische constanten, a is de roosterconstante en x is een molpercentage aluminium.

De variatie van polarisatielading ± σ _AlGaN (x ) met aluminiumpercentage is afgebeeld in Fig. 2a [3]. Zodra de polarisatielading is berekend, kan de Poisson-vergelijking worden opgelost. Bij AlGaN-GaN-interface verandert de geleidingsband abrupt en vormt een smalle (1-4 nm) driehoekige potentiaalkwantumbron waar elektronen zich ophopen. Omdat dit kwantumpotentieel erg smal is, wordt de verminderde dichtheid van de toestanden dominant. De kwantumvergelijking van Schrödinger verklaart de kwantumpotentiaal goed, maar is moeilijk op te lossen voor een groter HEMT-apparaat. Om het gedrag van de kwantumpotentiaalbron vast te leggen, hebben we het eQuantumpotentiaalmodel in de Sentaurus TCAD aangeroepen, dat het dichtheidsgradiënt-kwantumcorrectiemodel [23] activeert en een nauw overeenkomend resultaat geeft met de Schrodinger-kwantumvergelijking voor grotere HEMT-apparaten (power HEMT-apparaten). Het kwantummodel met dichtheidsgradiënt vermindert de piekwaarde van elektronendichtheid in 2DEG, en de piekwaarde verschuift ook weg van het AlGaN-GaN-interface. Dit vermindert dus het interface-verstrooiingsmechanisme en verbetert de mobiliteit in het kanaal, zie Fig. 2b [20]. Kwantummodel met dichtheidsgradiënt introduceert een extra term Λ in formule voor normale dichtheid, zoals:

$$n =N_{{\text{C}}} F_{1/2} \left( {(E_{{\text{F}}} - E_{{\text{C}}} - \Lambda ) /kT} \rechts)$$ (2)

waar N _C is de effectieve toestandsdichtheid, F 1/ 2 is Fermi-integraal van orde 1/ 2, E _F is de quasi-Fermi-energie voor elektronen, E _C is de geleidingsbandrand en kT vertegenwoordigt thermische energie van elektronen. Λ wordt berekend door:

$$\Lambda =- \left( {\left( {{{\gamma \hbar^{2} } \mathord{\left/ {\vphantom {{\gamma \hbar^{2} }} {6m_{n} }}} \right \kern-\nulldelimiterspace} {6m_{n} }}} \right) \cdot \left( {\nabla^{2} \sqrt n } \right)/\sqrt n } \right) $$ (3)

waar ħ = h /2π , h is plankconstante, m _n is een effectieve massa van het elektron, γ (γ = 1.28) is een passende parameter en n is elektronendichtheid.

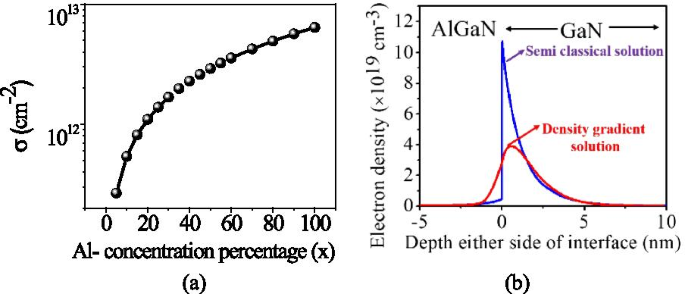
een Variatie van polarisatiebladlading met betrekking tot de aluminiumconcentratie in de AlGaN-barrièrelaag [3]. b Effect van kwantumgevangenschap op 2DEG-elektronendichtheid

De oppervlaktevallen werden geïntroduceerd als donorstaat (+ σ _D ) op het oppervlak van AlGaN-barrièrelagen Fig. 1a, en de simulatie werd uitgevoerd bij een temperatuur van 300 K. De kalibratie werd uitgevoerd met de initiële aluminiumconcentratie van 28%.

Simulatieresultaten en discussie

Effect van aluminiumpercentage en oppervlaktevallen op 2DEG-dichtheid

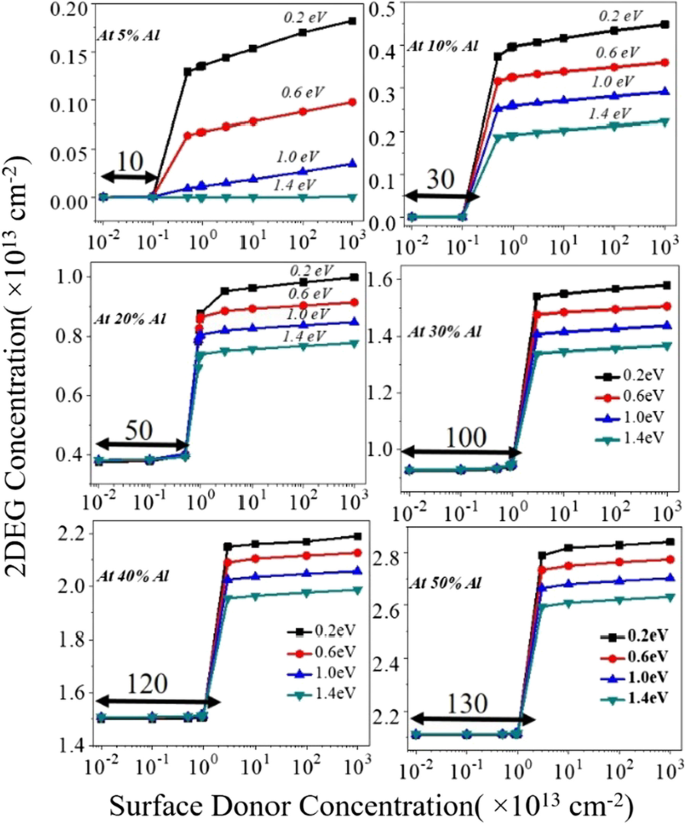
Het apparaat werd gesimuleerd zonder toegepaste bias-omstandigheden om de 2DEG-elektronendichtheid te onderzoeken. Terwijl we ons concentreren op de 2DEG-elektronendichtheid, is er voor alle energie van de donorstaat, tot een bepaalde waarde (relatief lagere waarde) van de donorvalconcentratie, geen significante verandering in de elektronendichtheid (d.w.z. Regio 1). 2DEG-elektronendichtheid verandert proportioneel met de oppervlaktedonorconcentratie (tussen Regio1 tot Regio2). Na een bepaalde drempelwaarde van de oppervlaktedonorval is er opnieuw geen verandering in de elektronendichtheid (d.w.z. Regio 2), zie Fig. 3a-d. Dit mechanisme kan als volgt worden uitgelegd:

een –d Variatie van elektronenbladdichtheid in 2DEG met oppervlaktedonorconcentratie en -energie (van ondiepe 0,2 eV tot diepe 1,4 eV) voor verschillende aluminiumpercentages. e Verschillende ladingsverdeling en elektrische veldoriëntatie in het apparaat

(i) De geleidingsband van de AlGaN-barrièrelaag voor regio1 heeft een grotere opening vanaf het Fermi-niveau aan het oppervlak. Naarmate de concentratie van de donorval van een lagere naar een hogere waarde begint toe te nemen, begint de geleidingsband in de overgangsperiode (tussen Regio1 naar Regio2) proportioneel te bewegen naar het Fermi-niveau. De 2DEG-concentratie begint dus toe te nemen van een lagere waarde naar een hogere waarde. In de overgangsperiode (tussen Regio1 naar Regio2) begint de geleidingsband proportioneel te bewegen naar het Fermi-niveau en dus beweegt de donoroppervlakte-energie ook naar het Fermi-niveau. Voor Regio2 begint zodra de donorconcentratie de drempelwaarde overschrijdt, de buiging van de geleidingsband zodanig dat de energie van de donorval het Fermi-niveau pinnen. Door Fermi level pining worden alle donortoestanden geïoniseerd en dragen ze elektronen bij aan de 2DEG driehoekige kwantumpotentiaalbron. Zodra de energie van donorstaten op het Fermi-niveau wordt vastgezet, weerspiegelt zich geen significante verandering in de elektronendichtheid. (ii) Om ladingsneutraliteit in het apparaat te vinden, zijn oppervlaktedonortoestanden essentieel om de elektronen in 2DEG tegen te gaan. Naarmate de toestand van de oppervlaktedonor toeneemt, begint een elektrisch veld toe te nemen van het oppervlak naar de 2DEG-kwantumbron. Dit elektrische veld gaat het ingebouwde elektrische veld tegen dat wordt geproduceerd door de lading van de polarisatieplaat (± σ _AlGaN ). Wanneer het externe elektrische veld het interne elektrische veld begint te overschrijden (vanwege ± σ _AlGaN ), het brengt de geleidingsband aan het oppervlak naar beneden en draagt dus meer elektronen bij aan de 2DEG-potentiaalbron, zie figuur 3e. Wanneer het aluminiumpercentage toeneemt van 5 tot 50%, neemt ook de ladingsdichtheid van het polarisatieblad proportioneel toe, wat leidt tot een hoog intern elektrisch veld (vanwege polarisatie). Om dit interne elektrische veld te overwinnen, is een hogere concentratie van oppervlaktedonorvallen vereist. Daarom wordt het overgangsgebied verschoven (van 10 naar 130 keer met 10¹¹ cm⁻² ) voor de hogere waarde van de donortrapconcentratie, waarbij de 2DEG-elektronendichtheid evenredig verandert met de donortrapconcentratie, Fig. 3a-d. 2DEG-concentratie voor elk aluminiumpercentage met betrekking tot de oppervlaktedonor (concentraat-+-energie) is uitgezet in Fig. 4. Ondanks dat het patroon van 2DEG-elektronenconcentratie hetzelfde is voor alle percentages aluminium wanneer de donorval van ondiep gaat (0,2 eV) tot diep (1,4 eV) (Fig. 5), is de verandering in 2DEG-elektronendichtheid van diep naar ondiep nog steeds behoorlijk significant. In het geval van een aluminiumconcentratie van 5% gaat de donorval van diep (1,4 eV) naar ondiep (0,2 eV), het draagt niet significant bij aan de potentiële bron. Als polarisatieladingsconcentratie (± σ ) is in de orde van 10¹¹ cm⁻² voor 5% aluminium zie figuur 2a, het elektrische veld als gevolg van deze polarisatieladingen is niet voldoende om de geleidingsbandverschuiving onder het Fermi-niveau te brengen, vandaar dat er geen 2DEG driehoekige potentiaalput wordt gevormd aan de GaN-zijde van de AlGaN-GaN-interfacestructuur. Het is ook duidelijk dat zelfs voor de hogere concentratie van oppervlaktedonorvallen de verzadiging van de elektronendichtheid niet optreedt zoals getoond in Fig. 4a en 6. Dit geldt ook voor 10% aluminiumpercentage zoals weergegeven in Fig. 4b. Voor 20% en meer is de concentratie polarisatielading (± σ) groter dan 10¹² cm⁻² . Dus het interne elektrische veld is groot genoeg om de offset van de geleidingsband onder het Fermi-niveau te trekken en daarom vormt het de 2DEG driehoekige kwantumpotentiaalbron, zie figuur 6b, c. Dus voor 20% en hoger aluminiumpercentage, benadert de 2DEG-elektronendichtheid ~ 10¹³ cm⁻² voor ondiepe donorvallen zoals getoond in Fig. 4c. Voor een aluminiumconcentratie van 20%, 30% en meer heeft de bijdrage van het elektron in de driehoekige put een dichtheid van 1 × 10¹³ tot 3 × 10¹³ cm⁻² . Figuur 5a,b toont de procentuele verandering van elektronendichtheid in driehoekige put wanneer de energie van de donorval verandert van 1,4e in 0,2eV. Naarmate we van 5 naar 50% aluminiumpercentage gaan, neemt de verandering in 2DEG-concentratie aanzienlijk af van 10,89 keer naar 1,08 keer en raakt verzadigd tot meer dan 30%.

Variatie van een individueel aluminiumpercentage tot donoroppervlakteval van diep naar ondiep met betrekking tot de geleidingsband

een Procentuele verandering op logschaal in 2DEG-elektronendichtheid voor Al-concentratie wanneer de oppervlaktedonor ondiep wordt van diep niveau ten opzichte van de geleidingsband. b Lineaire schaal

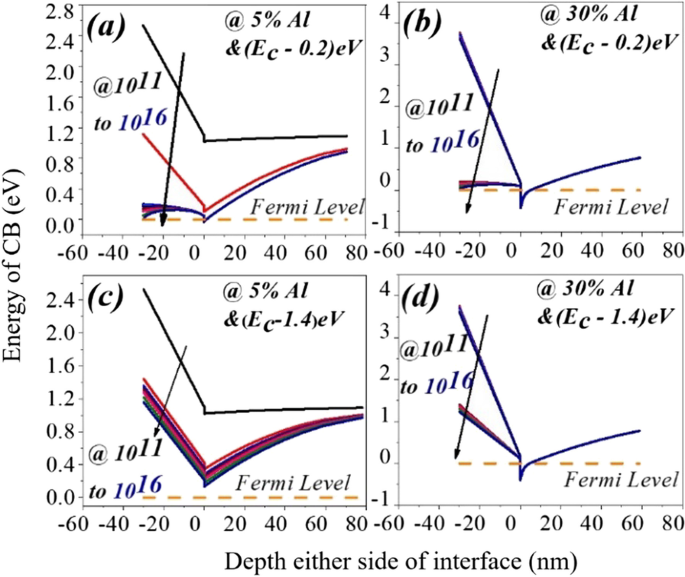
een , c Geleidingsbandvariatie aan weerszijden van de AlGaN-GaN-interface voor 5% aluminium en b , d voor 30% aluminium. Diepe oppervlakteval draagt geen elektronen- en positieve laaglading bij aan de potentiaalput en het oppervlak, waardoor de helling van de geleidingsband hoger wordt. Zelfs voor een diepe staat van het donoroppervlak (1,4 eV) is er een 2DEG-potentieel dat zich vormt voor 30% aluminium. Dit geldt niet voor 5% aluminium

Effect van aluminiumpercentage en oppervlakteval op oppervlaktepotentieel

Sommige literatuur heeft de oppervlaktepotentiaalvariatie besproken als gevolg van verandering in aluminiumpercentage [29]. Maar ze hebben het effect van oppervlaktedonorvallen op het oppervlaktepotentieel niet meegenomen. Hier rapporteren we de variatie van oppervlaktepotentieel als gevolg van oppervlaktedonorvallen, zowel in de dimensies van energie als concentratie, zie figuur 7a. In deze studie hebben we de oppervlaktedonorconcentratie gewijzigd van 1 × 10¹² tot 1 × 10¹⁶ en oppervlaktedonorenergie van 0,2 tot 1,4 eV. Oppervlaktepotentiaal is berekend uit Fig. 6b. Oppervlaktepotentiaal zakt in de buurt van 3,7 eV (voor oppervlaktedonorconcentratie 1 × 10¹² ) en 3,6 eV (voor oppervlaktedonorconcentratie 1 × 10¹³ ). Dit oppervlaktepotentieel is niet afhankelijk van de energie van de oppervlaktedonorval voor zijn lagere waarde. Het oppervlaktepotentieel neemt lineair toe naarmate de oppervlaktedonor diep gaat (1,4 eV) van ondiep (0,2 eV). Naarmate de oppervlaktepotentiaal daalt, zal de 2DEG-elektronenconcentratie toenemen omdat de oppervlaktepotentiaal lineair varieert met de energie van de oppervlaktedonorvanger. Het aluminiumpercentage heeft ook een grote invloed op het oppervlaktepotentieel. Door het aluminiumpercentage te verhogen van 5 naar 50%, neemt de elektronenconcentratie toe van 7,79 × 10¹¹ tot 2,75 × 10¹³ . Het oppervlaktepotentieel neemt ook toe van 0,49 tot 0,576 eV wanneer het aluminiumpercentage verandert van 5 tot 50%, zie figuur 7b. De concentratie en energie van de oppervlaktedonorvanger, samen met de aluminiumconcentratie, hebben dus een grote invloed op het oppervlaktepotentieel.

een Oppervlaktepotentiaalvariatie met betrekking tot energie van oppervlaktedonorval. Bij een lagere concentratie (minder dan 1e14) is er geen significante verandering in oppervlaktepotentiaal. Oppervlaktedonorconcentratie boven 1e13, oppervlaktepotentiaal verandert evenredig met de energie van oppervlaktedonor. b Elektronenconcentratie in 2DEG verandert van 7,79 × 10¹¹ tot 2,75 × 10¹³ voor aluminium procentuele veranderingen naar 50% van 5% (blauwe lijn). Oppervlaktepotentiaal verandert ongeveer 0,1 eV van 5 tot 50% van het aluminiumpercentage

Effect van aluminiumpercentage en oppervlakteval op geleidingsband en 2DEG-potentiaalbron

De geïoniseerde oppervlaktevallen dragen elektronen bij aan de potentiaalput en positieve vellading aan het AlGaN-oppervlak [6]. In het geval van een aluminiumconcentratie van 5%, als vallen diep gaan vanaf een ondiep energieniveau, wordt de hoeveelheid geïoniseerde oppervlaktevallen steeds kleiner. Aldus droegen geïoniseerde oppervlaktevallen minder elektronen bij aan driehoekige potentiaalput en positieve laagladingen aan het oppervlak. Een kleinere hoeveelheid positieve velladingen en elektronenconcentratie in 2DEG draagt niet genoeg bij aan het externe elektrische veld, en daarom wordt de helling van de geleidingsband in de AlGaN-laag groter, zoals weergegeven in figuur 6. Dit geldt ook voor aluminium met 10% in AlGaN-barrièrelaag. De vrije elektronen van de oppervlaktedonortoestanden bevinden zich in een 2DEG-potentiaalput en ze neutraliseren de positieve laaglading die aan het oppervlak van AlGaN verschijnt. Deze elektronenbladlading wordt berekend door [24]:

$$n_{{\text{s}}} (x) =\frac{ + \sigma (x)}{e} - \left( {\frac{{\varepsilon_{o} \varepsilon (x)}} {{de^{2} }}} \right)\left[ {e\phi_{{\text{b}}} (x) + E_{{\text{F}}} - \Delta E_{{\ tekst{C}}} (x)} \right]$$ (4)

waar d is de dikte van de Al_x Ga_{(1−x )} N barrièrelaag, ϕ _b is Schottky-barrière, E _F is het Fermi-niveau en ΔE _C is de offset van de geleidingsband bij de AlGaN-GaN-interface. Het blijkt uit vgl. (4) dat de ladingsdichtheid van de elektronenplaat recht evenredig is met de offset van de geleidingsband en de polarisatieladingen die een functie is van het aluminiumpercentage. Naarmate we het aluminiumpercentage verhogen van 10 naar 50%, neemt de geleidingsbandoffset toe [25] en dus neemt de elektronendichtheid in 2DEG toe als gevolg van de toename van het aantal energieniveaus, zie Fig. 8. Het interne elektrische veld van het apparaat, wanneer de aluminiumconcentratie 20% of meer is, is zodanig dat de helling van de geleidingsband hoog genoeg is om de driehoekige potentiaalput te construeren, zelfs voor diepe (1,4 eV) oppervlaktevangerenergie en lagere oppervlaktedonorvangerconcentratie zoals getoond in Fig. 6b, d .

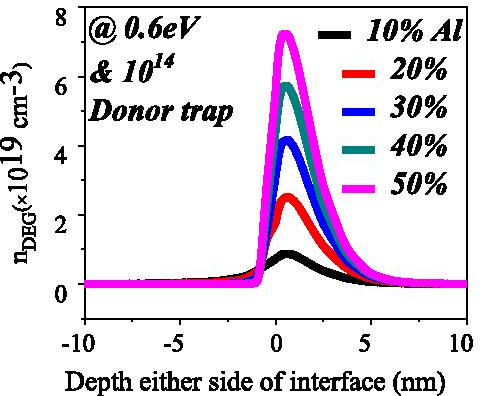
Elektronendichtheid in driehoekige kwantumpotentiaalput voor verschillende aluminiumconcentraties bij vaste donorconcentratie en energie

Het is belangrijk om te kijken naar de inkeping van de driehoekige kwantumpotentiaal die goed gevormd is onder het Fermi-niveau ((E _F − E) eV), waarbij E is de energie onder het Fermi-niveau. Twee belangrijke parameters in de driehoekige kwantumpotentiaalput zijn de diepte van de potentiaal ver onder het Fermi-niveau en de breedte van de potentiaalput op het Fermi-niveau. De opsluiting van de elektronen in tweedimensionale gebieden wordt het 2DEG-kwantumblad genoemd. De dichtheid van toestanden N (E ) is een van de belangrijke kenmerken in de 2DEG-kwantumpotentiaalbron. De toestandsdichtheid in tweedimensionale kwantumput wordt gedefinieerd als [26]:

$$N(E) =\left( {{{m^{*} L_{{\text{X}}}^{2} E} \mathord{\left/ {\vphantom {{m^{*} L_{{\text{X}}}^{2} E} {\pi \hbar^{2} }}} \right \kern-\nulldelimiterspace} {\pi \hbar^{2} }}} \ rechts)$$ (5)

waar m* is de effectieve massa van het elektron en L _X is de breedte van de put. Deze toestandsdichtheid in een tweedimensionale put ziet eruit als een stapfunctie.

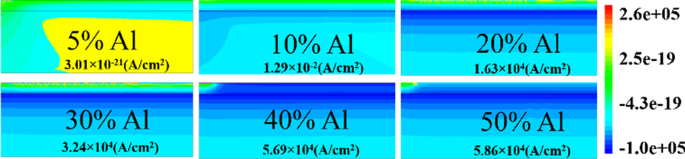
Het aantal bezette staten is afhankelijk van het Fermi-niveau. Als het Fermi-niveau bijvoorbeeld hoger is dan E ₁ maar minder dan E ₂; dan alleen E ₁ subband is gevuld. Als het Fermi-niveau hoger is dan E ₂ , maar minder dan E ₃ , dan twee lagere subband E ₂ en E ₁ zijn gevuld met elektronen zoals weergegeven in Fig. 9b. Dit betekent dat als de energie op het grensvlak dieper gaat met het Fermi-niveau, er alleen grote aantallen elektronen worden verwacht. In de AlGaN/GaN heterostructuur neemt de energie-afstand af ((E ₂ − E ₁ ) > (E ₃ − E ₂ )) voor hogere subbanden [27]. Naarmate de subbandenergie toeneemt, wordt het verschil tussen hen verwaarloosbaar en lijkt het continu. De rigoureus correcte oplossing van de golffunctie bevat tegelijkertijd de Poisson-vergelijking en de Schrodinger-vergelijking. Maar het dichtheidsgradiëntmodel genereert het ongeveer gelijke resultaat met de Schrodinger-vergelijking. In kwantumpotentiaalput wordt het energieniveau gekwantificeerd omdat deze put tot een paar nm lengtes vormt in de GaN-zijde van de AlGaN-GaN-interface. De diepere inkeping onder het Fermi-niveau zal zeker een hoger aantal gekwantificeerde energieniveaus hebben. Het gekwantificeerde energieniveau onder het Fermi-niveau is bezet. Vandaar dat, dieper de energie onder het Fermi-niveau, de elektronenconcentratie hoger zal zijn in 2DEG. Uit Fig. 9a is het duidelijk dat het energieniveau onder het Fermi-niveau hoger wordt wanneer het aluminiumpercentage toeneemt, omdat de polarisatielading toeneemt en dus het interne elektrische veld de inkeping dieper maakt. Wat de energie van de oppervlaktedonor betreft, blijkt uit de vorige discussie dat wanneer de oppervlaktevallen dieper gaan (1,4 eV), de ionisatie van deze oppervlaktedonoren afneemt. Daarom wordt het elektrische veld gegenereerd als gevolg van positieve laagladingen aan het oppervlak en zijn elektronen die door deze oppervlaktedonoren aan 2DEG worden bijgedragen niet voldoende om het interne elektrische veld te overwinnen. Het effect van polarisatielading in termen van elektrisch veld vermindert dus, wat leidt tot minder energieniveaus onder het Fermi-niveau. Een uitzondering is voor 5% aluminiumconcentratie, het is duidelijk uit Fig. 10a die waarde van E _F − E is negatief omdat het Fermi-niveau wordt aangenomen op nulniveau, voor de diepe donorvallen (>-0,9 eV tot 1,4 eV), wat betekent dat de energie E hoger is dan het Fermi-niveau (2DEG vormt zich niet). Voor ondiepere donorvallen (< 0,9 eV tot 0,2 eV), de waarde van E _F − E is positief, wat betekent dat de waarde van de E lager is dan het Fermi-niveau. Voor de rest van de aluminiumconcentratie (10% tot 50%) is de waarde van E _F − E positief is, wat betekent dat de waarde van E lager is dan het Fermi-niveau en er wordt een 2DEG-inkeping gevormd voor alle soorten oppervlaktedonorenergie (van 0,2 eV tot 1,4 eV). Uit figuur 11a blijkt dat de procentuele verandering van energie E met aluminium verzadigd raakt boven 20% aluminiumconcentratie, wat ook in overeenstemming is met Fig. 5. De diepte van de inkeping onder het Fermi-niveau verandert niet significant na 20% aluminiumconcentratie wanneer de oppervlaktedonor de energieverandering van diep naar ondiep opvangt. Figuur 11b laat ook zien dat er geen significante stroom is tot 10% aluminiummolfractie. Boven 10% is er een significante verandering in stroom wanneer de energie van de oppervlaktedonor verandert van E _C − 0.2 tot E _C − 1.4 eV en weer meer dan 20% verzadigd. Dit resultaat is ook in overeenstemming met Fig. 11a en 5. De contourgrafiek van absolute stroomdichtheid laat ook zien dat deze verzadigt boven 20% Al-molfractie en geen significante stroomdichtheid tot 10% van Al-molfractie Fig. 12. Dit valideert ook niet-vorming van 2DEG tot 10% Al mol fractie. Een significante hoeveelheid elektronendichtheid waargenomen boven 20% van de molfractie Fig. 13a. Elektrisch velddistributie langs het kanaal is uitgezet in figuur 13b. Figuur 13b laat zien dat er geen opmerkelijk verbeterd elektrisch veld onder de poort is tot 10% van de Al-molfractie en boven 20% van de Al-molfractie is er niet veel verschil in elektrisch veld, wat de stroom bij een hoger Al-percentage beperkt.

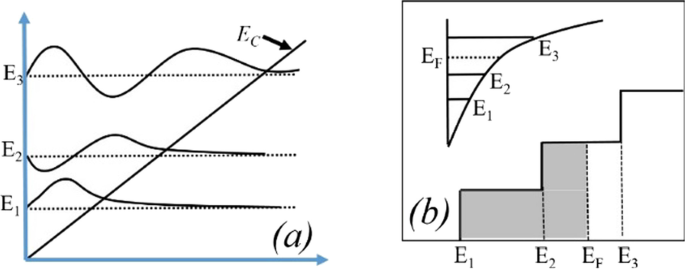
een Een driehoekig potentieel dat subbandenergieën goed weergeeft met Fang–Howard Airy Golf functie. b Alleen subbanden met lagere energie (E ₁ en E ₂ , lager dan Fermi-niveau) zijn bezet [28]

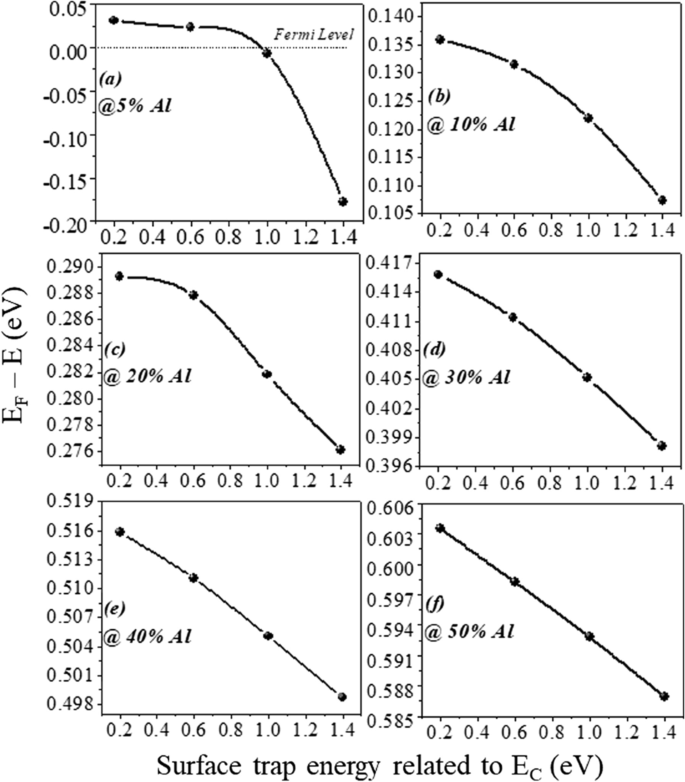
een –f (E _F − E ) variatie met oppervlaktedonorenergie voor alle aluminiumconcentraties

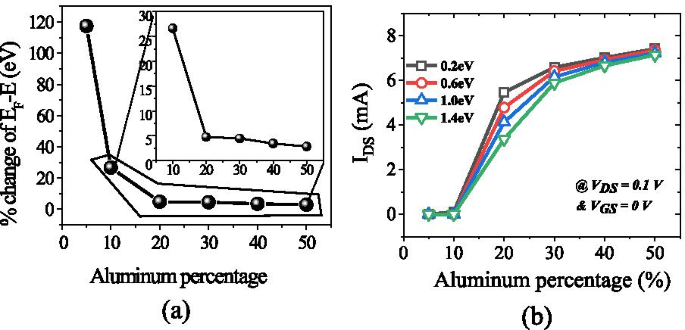
een De procentuele verandering van energie E met aluminiumconcentratie wanneer de energie van de oppervlaktedonor diep in ondiep verandert. b Afvoerstroom en V _DS = 0.1 V en V _GS = 0 V bij verschillende oppervlaktedonoren vangen energie op. Tot 10% geen significante stroom waargenomen in het apparaat

Contourgrafiek van absolute totale stroomdichtheid voor 0,6 eV oppervlaktedonorenergie bij V _DS = 0.1 V en V _GS = 0 V

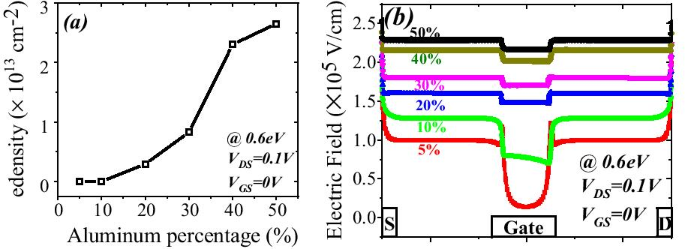
een Electron density variation with aluminum percentage and b electric field variation below gate and either side of gate for different aluminum percentage

Conclusion

In this paper, we comprehensively present the effect of surface donor traps along with aluminum percentage on electron density and quantum potential well. This manuscript demonstrated that the percentage change happens in 2DEG and notch below the Fermi level gets saturated above 20% of aluminum concentration when surface donor trap energy goes deep to shallow. The electron density in the two-dimensional quantum potential well is saturated approximately at 8%, whereas the energy below the Fermi level saturates somewhere around 2%. These two results are also in tune with each other, except 5% aluminum, having a condition for not forming two-dimensional well for relatively deep (> 0.9 eV) surface donors. Aluminum percentage above 10% forms two-dimensional quantum potential well even for deeper surface donor traps. The effect of surface donor traps on the surface potential also has been discussed in this work. The results of this paper may provide the impetus to the experimental result validation.

Availability of data and materials

All data are available on request.

Abbreviations

GaN:: Gallium nitride
HEMT:: High-electron-mobility transistor
2DEG:: Two-dimensional electron gas
DD:: Drift and diffusion transport model
SRH:: Shockley–Read–Hall recombination model

N,N-dimethylformamide die de fluorescentie van MXene Quantum Dots reguleert voor de gevoelige bepaling van Fe3+ Volledig diëlektrisch fasegradiëntmetasurface dat zeer efficiënte abnormale transmissie uitvoert in het nabij-infraroodgebied

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal