Volledig diëlektrisch fasegradiëntmetasurface dat zeer efficiënte abnormale transmissie uitvoert in het nabij-infraroodgebied

Abstract

We stellen een fase-gradiënt meta-oppervlak voor en demonstreren dit numeriek met een hoge abnormale transmissie-efficiëntie en een grote abnormale brekingshoek die bestaat uit discontinue regelmatige hexagonale nanostaafjes ondersteund door een silicasubstraat. Het meta-oppervlak bereikt een hoge abnormale transmissie-efficiëntie en een volledige 2$\pi$ faseverschuiving voor het golflengtebereik van 1400-1600 nm. Bij een centrale golflengte van ongeveer 1529 nm bereikt de totale transmissie-efficiëntie 96,5%, en de gewenste abnormale transmissie-efficiëntie bereikt 96,2%, met een afwijkende brekingshoek zo groot als 30,64. Met de aanpassing van de periode en het aantal nanostaafjes per periodiek interval, overschrijdt de abnormale transmissie-efficiëntie 69,6% voor een grote abnormale brekingshoek van 68,58. De superieure prestaties van het voorgestelde ontwerp kunnen de weg vrijmaken voor toepassing in optische golffrontbesturingsapparaten.

Inleiding

In de afgelopen jaren hebben fase-gradiënt meta-oppervlakken steeds meer aandacht getrokken, omdat ze een nieuw pad hebben geboden voor geavanceerde golffront-engineering [1,2,3,4,5,6,7]. Vergeleken met conventionele golffrontcontroleapparaten zijn fasegradiëntmeta-oppervlakken veel flexibeler, waardoor het mogelijk is om de amplitude en fase van licht te moduleren [8,9,10,11]. Bovendien zijn ze als een soort tweedimensionaal metamateriaal makkelijker toepasbaar op het gebied van fotonische integratiesystemen. Aangezien Yu et al. een V-vormige antenne-array voorgesteld als een fase-gradiënt meta-oppervlak en het concept van de gegeneraliseerde brekingswet in detail uitgelegd [12], verschillende fase-gradiënt meta-surfaces op basis van discrete nano-antenne-arrays zijn voorgesteld en onderzocht [2,3,4, 5,6,7,8,9,10,11,12,13]. Bijvoorbeeld, Liu et al. introduceerde een gouden rooster in een V-vormige gouden antenne-array, waardoor de abnormale transmissie-efficiëntie tot 15 keer groter werd dan zonder een gouden rooster [14]. Meta-oppervlakken met fasegradiënt zijn in veel gebieden gebruikt en hun toepassingen omvatten deflectors [8, 15,16,17], directionele oppervlaktegolfkoppelaars [18, 19], holografische apparaten [20,21,22] en vortexbundelgeneratoren [23,24,25]. Hoewel de toepassingsvooruitzichten van op metaal gebaseerde meta-oppervlakken op veel gebieden zijn geverifieerd, worden de prestaties van meta-oppervlakken meestal beperkt door de zeer hoge intrinsieke ohmse verliezen van de metalen materialen [26, 27]. Omdat diëlektrische materialen geen intrinsiek ohms verlies hebben, hebben mensen geprobeerd metalen materialen te vervangen door diëlektrische materialen bij het ontwerpen van volledig diëlektrische meta-oppervlakken met hoge prestaties [28, 29].

Meer recentelijk was de gemeenschappelijke uitdaging bij het gebruik van volledig diëlektrische fasegradiëntmeta-oppervlakken de moeilijkheid om een hoge abnormale transmissie-efficiëntie te bereiken met een grote abnormale brekingshoek. Om dit probleem op te lossen, Zhou et al. ontwierp een meta-oppervlak bestaande uit een gradiëntarray van cirkelvormige silicium nanostaafjes gerangschikt op een kwartssubstraat, en bereikte een abnormale transmissie-efficiëntie van 71% met een abnormale brekingshoek van 19,27 [6]. Yang et al. ontwierp een volledig diëlektrisch meta-oppervlak op basis van silicium nanoantennes voor zeer efficiënte abnormale transmissie, waarvan de abnormale transmissie-efficiëntie 80,5% bereikte met een abnormale brekingshoek van 29,62 [30]. In 2019 bereikte de abnormale transmissie-efficiëntie van een volledig diëlektrisch meta-oppervlak, mogelijk gemaakt door een kruisvormige structuur, 83,5% met een abnormale brekingshoek van 30 [31]. In het bijzonder David Sell et al. een periodiek diëlektrisch meta-oppervlak voorgesteld en experimenteel onderzocht. In dit werk waren de auteurs in staat om numeriek en experimenteel abnormale breking waar te nemen met een hoog rendement (> 90%) voor uitgaande hoeken tot 50 [32]. Bovendien hebben sommige onderzoekers de voordelen van hyperbolische metamaterialen met breedband en hoge dubbele breking gebruikt om een hoge transmissie-efficiëntie te bereiken [33, 34].

In dit werk is ons doel om een volledig diëlektrisch meta-oppervlak te ontwerpen om tegelijkertijd een hoge abnormale transmissie-efficiëntie te verkrijgen en de abnormale brekingshoek te vergroten. Het voorgestelde meta-oppervlak bestaat uit discontinue regelmatige hexagonale silicium nanostaafjes ondersteund door een silicasubstraat. We analyseren systematisch de afwijkende transmissie-efficiëntie en de afwijkende brekingshoek van de voorgestelde structuur met behulp van de eindige-verschil tijdsdomein (FDTD) methode. De resultaten laten zien dat bij een centrale golflengte van 1529 nm de totale transmissie-efficiëntie van het diëlektrische meta-oppervlak 96,5% kan bereiken; bovendien kan de doorsnede van het gewenste afwijkende transmissierendement oplopen tot 96,2% met een afwijkende brekingshoek van 30,64. De afwijkende brekingshoek kan worden vergroot door het aantal elementen per periodiek interval en de periode aan te passen. We demonstreren numeriek een afwijkende brekingshoek die 68,58 bereikt met een afwijkende transmissie-efficiëntie van wel 69,7% voor een centrale golflengte van 1536 nm. Er wordt aangenomen dat het voorgestelde volledig diëlektrische meta-oppervlak een cruciale rol zal spelen in geavanceerde golffront-engineering.

Ontwerp en methoden

Voor een meta-oppervlak met fasegradiënt hebben de geometrische morfologie en parameters een grote invloed op de prestaties van het apparaat. Zoals getoond in Fig. 1 onderzoeken we eerst een eenvoudige matrixstructuur die is samengesteld uit regelmatige hexagonale nanostaafjes op basis van een silicasubstraat. De transmissie-efficiëntie en faseverdelingen van de eenvoudige array-structuur worden geanalyseerd met behulp van de FDTD-methode. In de simulatie is de x - en y -richtingen worden ingesteld als periodieke randvoorwaarden, en de z -richting is ingesteld als perfect op elkaar afgestemde lagen. We hebben een normale transversale elektrische (TE) golf ingesteld om op de bodem te vallen. De elektrische veldrichting van het invallende licht is langs de y -richting, en het golflengtebereik is 1400-1600 nm. In de numerieke analyse zijn de brekingsindexen van silicium en silicium ontleend aan de gegevens die zijn voorgesteld door Palik [35]. Om een half onbeperkt silicasubstraat te fabriceren, moet experimenteel een etsproces worden uitgevoerd. We moeten ook een siliciumfilm van 1200 nm op het silicasubstraat deponeren met behulp van de lagedruk-chemische dampafzetting (LPCVD)-methode. De siliciumfilm wordt spin-gecoat met ZEP520A-fotoresist en vervolgens wordt een dunne laag Cr als resist afgezet. Zeshoekige diëlektrische nanostaafjes kunnen worden verkregen door elektronenstraallithografie (EBL). Ten slotte worden verwijderaar 1165 en $O_2$ plasma gebruikt om de fotoresist te verwijderen, wat het ontworpen volledig diëlektrische fase-gradiënt meta-oppervlak oplevert [4, 6]. De dwarsdoorsnede van regelmatige hexagonale nanostaafjes kan echter op een cirkel lijken vanwege nabijheidseffecten in praktische experimentele fabricage. Om dit probleem op te lossen, kunnen we de nabijheidseffectcorrectie (PEC) en de dosis EBL aanpassen aan de monstermorfologie. Door het schema aan te passen, denken we dat we uiteindelijk nauwkeurig vervaardigde regelmatige zeshoekige meta-oppervlakken kunnen verkrijgen.

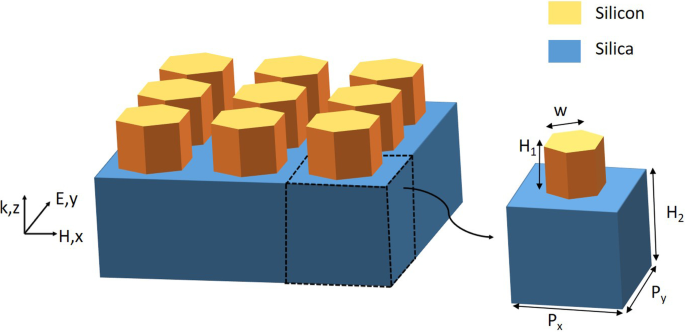
Schema van een eenvoudige matrixstructuur bestaande uit regelmatige hexagonale silicium nanostaafjes op een silicasubstraat

Anders dan de ideale grens, veranderen optische eigenschappen, zoals de polarisatietoestand, fase en golffront, aanzienlijk wanneer licht zich door het meta-oppervlak voortplant. We kunnen deze verschijnselen niet verklaren met de klassieke wet van Snellius in geometrische optica wanneer elektromagnetische golven zich door deze interfaces voortplanten, wat aanleiding geeft tot een universele gegeneraliseerde wet van Snellius [8,9,10,11,12]. Op basis van de gegeneraliseerde wet van Snell treedt abnormale reflectie of breking op het grensvlak van twee media op vanwege de horizontale faseverdeling. We kunnen de twee soorten breking uitdrukken als

$$\begin{uitgelijnd} \begin{uitgelijnd} n_r\sin \theta _r-n_i\sin \theta _i =\frac{\lambda _0}{2\pi }\frac{{\hbox {d}}\phi }{{\text {d}}x} \end{uitgelijnd} \end{uitgelijnd}$$ (1)

waarbij $\theta _r$ de brekingshoek of afwijkende brekingshoek voorstelt en $\theta _i$ de invalshoek voorstelt. De brekingsindex $n_r$ verwijst meestal naar de brekingsindex van lucht, die een grootte van 1 heeft. Daarentegen verwijst $n_i$ naar de brekingsindex van het meta-oppervlak, $\lambda _0$ is de werkende golflengte in de vrije ruimte, en d$\phi$/${\text {d}}x$ is de fasegradiënt. Het fase-gradiënt meta-oppervlak moet een volledige bijna-lineaire $2\pi$ faseverschuiving bereiken over een grote periode om de abnormale transmissie te beheersen; dus de fasegradiënt is

$$\begin{uitgelijnd} \begin{uitgelijnd} \frac{{\hbox {d}}\phi }{{\text {d}}x} =\frac{2\pi }{P_x} \end{uitgelijnd } \end{uitgelijnd}$$ (2)

waarbij $P_x$ de periode is van het voorgestelde meta-oppervlak langs de x -as. In dit werk beschouwen we alleen het normale licht dat op de interface valt; dus $\theta _i$ is 0, en de vergelijking kan verder worden vereenvoudigd als

$$\begin{aligned} \begin{aligned} sin\theta _r =\frac{\lambda _0}{2\pi }\frac{{\hbox {d}}\phi }{{\text {d}} x} =\frac{\lambda _0}{P_x} \end{uitgelijnd} \end{uitgelijnd}$$ (3)

Fase-gradiënt meta-oppervlakken vertonen niet alleen abnormale transmissie van lage orde, maar ook abnormale transmissie van hoge orde. Om de abnormale brekingshoek van hoge orde te bepalen, introduceren we de roostervergelijking om de algemene wet van Snell te wijzigen [36,37,38]. De gewijzigde gegeneraliseerde wet van Snell is

$$\begin{aligned} \begin{aligned} \sin\theta _r =m\frac{\lambda _0}{P_x}+\frac{\lambda _0}{P_x} =(m+1)\frac{\ lambda _0}{P_x} \end{uitgelijnd} \end{uitgelijnd}$$ (4)

waar m vertegenwoordigt de traditionele diffractievolgorde. Elektromagnetische golfverschuivingen van de positie van de oorspronkelijke nulde orde naar de positie van de eerste orde kunnen worden gebruikt om de afwijkende brekingshoek te bepalen. Bovendien bepalen de periode en de werkingsgolflengte het totale aantal diffractieorders. De verhouding van $\lambda _0$ tot $P_x$ beïnvloedt de gewenste waarde van m. Als $\lambda _0$/$P_x$ groter is dan 0,5, m kan alleen een waarde van 0 aannemen, in welk geval er slechts drie diffractieorden kunnen worden verkregen:0, −1 en 1. Echter, wanneer $\lambda _0$/$P_x$ kleiner is dan 0,5, m kan een waarde van 0 of 1 aannemen, in welk geval vijf diffractieorden kunnen worden verkregen:$-2, -1, 0, 1$, en 2. In de volgende discussie wordt deze theorie bewezen door onze berekende resultaten .

Om de kenmerken van de voorgestelde structuur uit te leggen, berekenen we voornamelijk het rendement en de brekingshoek voor abnormale transmissie. De totale transmissie-efficiëntie en de abnormale transmissie-efficiëntie worden gedefinieerd als

$$\begin{aligned} T=I_{\mathrm{out}}/I_{\mathrm{in}} \end{aligned}$$ (5) $$\begin{aligned} \eta=I_r/I_{ in} \end{uitgelijnd}$$ (6)

waarbij $I_{\mathrm{in}}$ de ingangsintensiteit is, $I_{\mathrm{out}}$ de totale transmissie-intensiteit is, en $I_r$ de uitgezonden intensiteit langs de afwijkende breking is hoek.

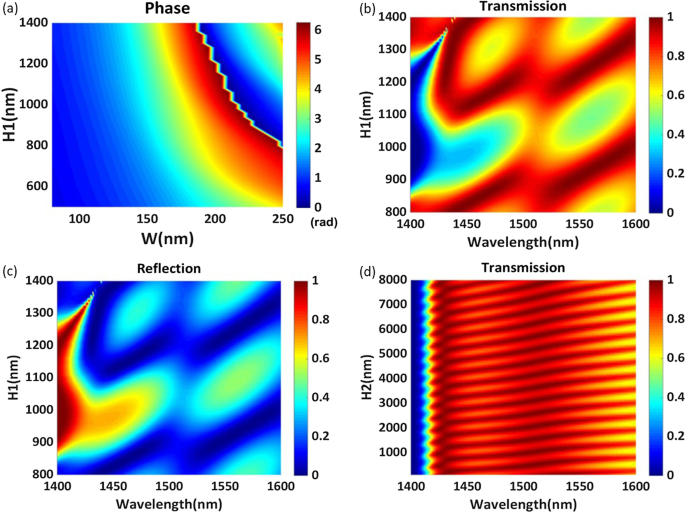
een Fase van de periodieke regelmatige hexagonale nanostaafjes voor verschillende structurele parameters $H_1$ en w bij een golflengte van 1529 nm. b De transmissie-efficiëntie en c de reflectie-efficiëntie van de periodieke structuur voor verschillende diktes $H_1$ in het golflengtebereik van 1400-1600 nm. d Transmissie-efficiëntie van de periodieke structuur voor verschillende diktes $H_2$ in het golflengtebereik van 1400-1600 nm

Voor de voorgestelde structuur hopen we een volledige 2$\pi$ faseverschuiving te bereiken door de hoogte $H_1$ en de zijlengte van de regelmatige zeshoek w aan te passen . We stellen de periode P . in tot 500 nm, en stel de substraatdikte $H_2$ in op 7050 nm. Aangezien de substraatdikte $H_2$ groter is dan $4\lambda$, kunnen we het substraat als een half onbeperkt substraat beschouwen. De fasevariaties met de verandering in $H_1$ en w bij een golflengte van 1529 nm worden getoond in Fig. 2a. Het is duidelijk dat de fase van doorvallend licht varieert met de lengte van de zijde van de regelmatige zeshoek w , maar alleen wanneer de hoogte $H_1$ groter is dan 800 nm kan deze structuur een volledige 2$\pi$ faseverschuiving realiseren. Hoge transmissie-efficiëntie is een andere factor waarmee rekening moet worden gehouden bij het ontwerpen van meta-oppervlakken met fasegradiënt. Figuur 2b, c toont de veranderingen in de transmissie-efficiëntie en reflectie-efficiëntie met de golflengte voor verschillende hoogten $H_1$ van de periodieke nanostaafjes, weergegeven in figuur 1. De structurele parameter w is ingesteld op 160 nm. Zoals weergegeven in figuur 2b, verschuift de golflengte van de piektransmissie-efficiëntie rood met toenemende nanostaafhoogte. Het is duidelijk dat de hoogte van de nanostaafjes een opmerkelijk effect heeft op de transmissie-efficiëntie en reflectie-efficiëntie. Om een hoge transmissie-efficiëntie te verkrijgen, wordt hier de hoogte $H_1$ ingesteld op 1200 nm. Bij deze waarde is de hoogste transmissie-efficiëntie van het eenvoudige homogene meta-oppervlak zo hoog als 98,70% bij een golflengte van 1540 nm. Figuur 2d beschrijft de verandering in transmissie-efficiëntie met de golflengte voor verschillende hoogtes $H_2$. De transmissie-efficiëntie verandert periodiek met toenemende substraatdikte $H_2$.

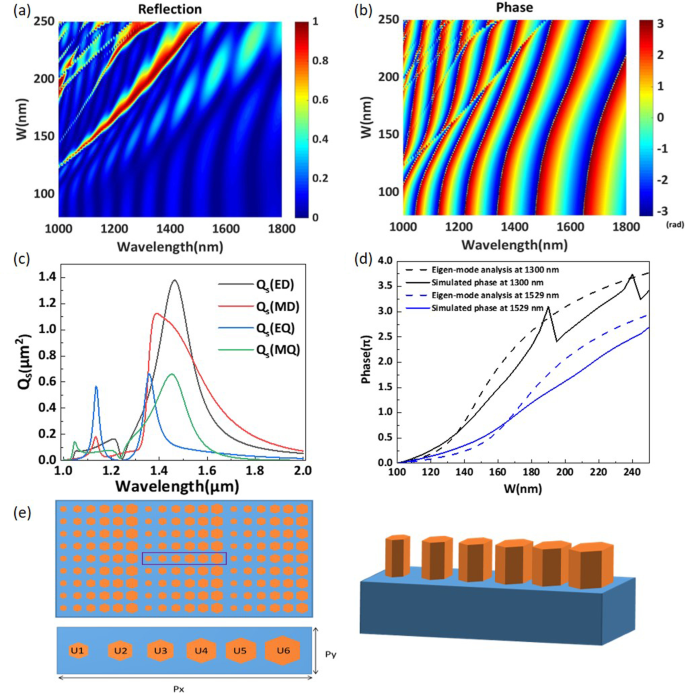
een De reflectie-efficiëntie en b de fase van de periodieke regelmatige hexagonale nanostaafjes voor verschillende waarden van w in het golflengtebereik van 1000-1800 nm. c Verstrooiingsdoorsnede $Q_s$ versus de golflengte van een geïsoleerde regelmatige hexagonale silicium nanostaaf. De bijdrage van elke term aan de Mie-uitbreiding wordt weergegeven. d Faseprofielen verkregen via eigenmode-analyse en numerieke simulaties voor variërende zijlengte w . e Schema van het ontworpen fase-gradiënt meta-oppervlak

Figuur 3a, b illustreert de variatie in de reflectie-efficiëntie en fase van de eenvoudige arraystructuur door de zijlengte van de regelmatige zeshoeken te veranderen voor het golflengtebereik van 1000-1600 nm. Zoals getoond in Fig. 3a, b, zijn er veel te onderscheiden resonantiepieken in het reflectiespectrum. Door de eenvoudige arraystructuur kan voor elke resonantiegolflengte een bijna $\pi$ faseverschuiving worden gerealiseerd. Het is duidelijk dat een volledige $2\pi$ faseverschuiving kan worden bereikt wanneer de zijdelengte van de regelmatige zeshoek w verandert van 100 naar 220 nm bij een golflengte van 1529 nm. Om het mechanisme van de $2\pi$ faseverschuiving verder te verduidelijken, gebruiken we de elektromagnetische multipole expansie (EME) methode om de verstrooiingsdoorsneden (SCS's) van een geïsoleerde regelmatige hexagonale silicium nanostaaf te berekenen [31, 41]. In Fig. 3c plotten we de berekende verstrooiende SCS's van de elektrische dipool (ED), magnetische dipool (MD), elektrische quadrupool (EQ) en magnetische quadrupool (MQ) componenten voor w =160 nm. Het is duidelijk dat verschillende Mie-resonanties, in het bijzonder dipoolresonanties, worden geëxciteerd bij de werkende golflengte. Er zijn echter enkele afwijkingen tussen de excitatie van de Mie-resonanties in het geïsoleerde deeltje en die in de periodieke deeltjes. Er is geen abrupte faseverandering bij een golflengte van 1529 nm, wat bewijst dat de $2\pi$ faseverschuiving wordt gevormd door slechts één modus. Daarom wordt het $2\pi$ fasecontrolemechanisme bij een golflengte van 1529 nm geanalyseerd door eigenmode-analyse [42]. Deze nanostaafjes kunnen worden beschouwd als Fabry-Pérot-resonatoren met een lage kwaliteitsfactor, en de fase kan worden gemoduleerd door de effectieve brekingsindex van de fundamentele modus. Zo kan worden aangetoond dat de fase is

$$\begin{aligned} \begin{aligned} \varphi =H_1*n_{\mathrm{eff}}*2\pi /\lambda \end{aligned} \end{aligned}$$ (7)

waarbij $H_1$ de hoogte is van deze nanostaafjes, $n_{\mathrm{eff}}$ de effectieve brekingsindex is van de fundamentele modus die wordt verkregen door eigenmodusanalyse, en $\lambda$ de werkende golflengte is . In Fig. 3d plotten we de faseprofielen die zijn verkregen via eigenmode-analyse (stippellijn) en numerieke simulatie (ononderbroken lijn) bij golflengten van respectievelijk 1300 nm en 1529 nm. Zoals weergegeven in figuur 3d, zijn er twee abrupte faseverminderingen in de gesimuleerde fase bij een golflengte van 1300 nm, wat overeenkomt met twee soorten Mie-resonanties. Wanneer w veranderingen van 100 naar 250 nm, zijn de faseveranderingstrends die door de twee methoden worden verkregen in principe hetzelfde bij een golflengte van 1529 nm. Volgens de roodverschuiving van de reflectiepieken in Fig. 3a, wanneer w groter is dan 250 nm, wordt de Mie-resonantie geëxciteerd bij een golflengte van 1529 nm. Voor het meta-oppervlak dat we in dit werk voorstellen, aangezien de structurele parameters van elk element in het bereik van 100 tot 220 nm liggen, zoals weergegeven in tabel 1, worden er geen Mie-resonanties aangeslagen binnen dit bereik. Daarom kunnen we aannemen dat de faseverschuiving voornamelijk gebaseerd is op de Fabry-Pérot-resonantie [6, 39, 40, 42]. Volgens de algemene wet van Snellius kan abnormale transmissie worden bereikt als een meta-oppervlak een $2\pi$ faseverschuivingsvermogen heeft. Door de grootte van de nanostaafjes zo aan te passen dat de faseverschuiving gelijkmatig verdeeld is en een volledig $2\pi$ bereik bestrijkt, kunnen we de straal afbuigen door zijn golffront te ontwrichten. Figuur 3e illustreert het schematische diagram van het fase-gradiënt meta-oppervlak. Zes silicium nanostaafjes van verschillende grootte met $2\pi /5$ fase-intervallen zijn gerangschikt op een silicasubstraat om een volledige fasegradiënt van 0 tot $2\pi$ te vormen. Het paarse vak vertegenwoordigt een volledige periode en $P_x$ en $P_y$ zijn respectievelijk ingesteld op 3000 nm en 500 nm.

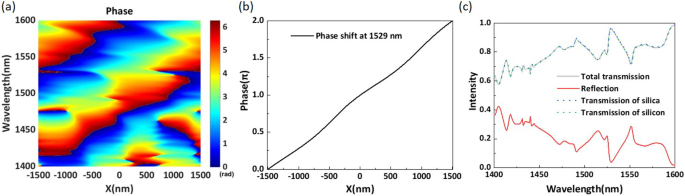
een Gesimuleerde faseverschuiving van het meta-oppervlak langs de x -richting in een volledige periode voor het golflengtebereik van 1400-1600 nm. b Gesimuleerde faseverdeling langs de x -richting bij een golflengte van 1529 nm. c Gesimuleerde intensiteiten van het doorgelaten en gereflecteerde licht

Resultaten en discussie

Tabel 1 toont de structurele parameters van elk element voor de voorgestelde structuur. We onderzoeken de faseverdeling en intensiteit van het doorgelaten licht. Om de analyse te vergemakkelijken, stellen we de oorsprong van de coördinaten in als het centrum van de supercel. We simuleren de faseverdeling van het doorgelaten licht in het golflengtebereik van 1400-1600 nm. Zoals weergegeven in figuur 4a, kan de voorgestelde structuur een volledige $2\pi$ faseverschuiving realiseren in het bereik van 1400-1600 nm. Om dit duidelijk te maken, toont figuur 4b de faseverschuivingscurve bij een centrale golflengte van 1529 nm. Zoals weergegeven in figuur 4b, vertoont de faseverschuiving een lineaire trend en is deze erg vloeiend. Volgens de algemene wet van Snell geldt:hoe beter de lineariteit van de faseverschuiving, hoe vlakker het uitrustfasevlak van het doorgelaten licht. We simuleren de transmissie en de reflectie van het voorgestelde meta-oppervlak voor het bereik van 1400-1600 nm, waarvan de resultaten worden getoond in figuur 4c. Door de curve te observeren, kunnen we zien dat de totale transmissie zeer efficiënt blijft, meer dan 60% over het hele golflengtebereik. Bij een golflengte van 1529 nm bereikt de totale transmissie-efficiëntie 96,5% met een reflectie-efficiëntie van 3,4%. De som van de reflectiviteit van de structuur en de transmissie van het silicasubstraat is 1 in het gehele golflengtebereik. Daarom kunnen we vaststellen dat de reflectie voornamelijk plaatsvindt op het eerste grensvlak tussen de lucht en het substraat. Zoals te zien is in figuur 4c, zijn de verschillen tussen de drie transmissiecurven nauwelijks waarneembaar en worden ze veroorzaakt door absorptie van de structuur. De absorptiesnelheid is veel minder dan 0,1% omdat het denkbeeldige deel van de brekingsindex van silicium in het nabij-infrarode golflengtebereik erg klein is. De absorptiesnelheid is dus verwaarloosbaar. De transmissie-efficiëntie en reflectie-efficiëntie vertonen tegengestelde trends aan die van de golflengte, en het verlies van de structuur komt voornamelijk door reflectie. Het is duidelijk dat het voorgestelde meta-oppervlak met fasegradiënt een volledige bijna lineaire $2\pi$ faseverschuiving kan realiseren en tegelijkertijd een hogere transmissie-efficiëntie in het bereik van 1400-1600 nm kan behouden.

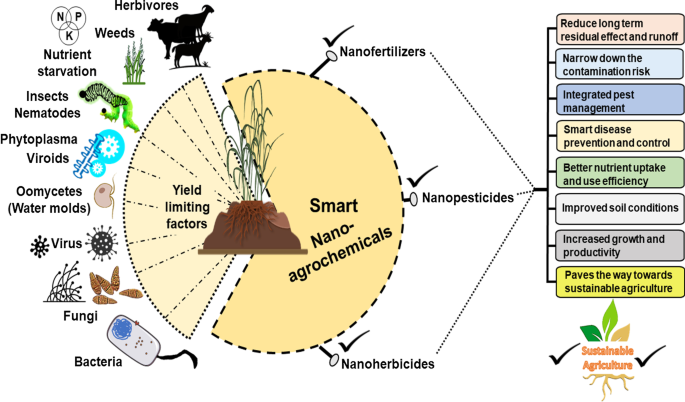
een Gesimuleerde intensiteit van de afwijkende transmissie-efficiëntie. b Verre-veld transmissie-efficiëntie voor verschillende afwijkende brekingshoeken bij een golflengte van 1529 nm. c Faseverdeling van de meta-oppervlakconfiguratie bij een golflengte van 1529 nm. De hoek in de afbeelding toont de brekingshoek van afwijkend doorvallend licht

Zoals getoond in Fig. 5a, berekenen we ook de gewenste abnormale transmissie-efficiëntie van het fasegradiënt-meta-oppervlak over het hele golflengtebereik van de werking en normaliseren deze naar de energie van het invallende licht. Als we Fig. 4c vergelijken met Fig. 5a, kunnen we zien dat de trends van de totale transmissie-efficiëntie en abnormale transmissie-efficiëntie met de golflengte consistent zijn. De resultaten laten zien dat de gewenste afwijkende transmissie-efficiëntie 80% overschrijdt in het golflengtebereik van 1527-1545 en 1591-1600 nm. Opmerkelijk is dat de afwijkende transmissie-efficiëntie maar liefst 96,2% is bij een golflengte van 1529 nm. Figuur 5b toont de relatie tussen de transmissie-efficiëntie in het verre veld en de afwijkende brekingshoek bij een golflengte van 1529 nm. Het is duidelijk dat de verre-veldenergie van het doorgelaten licht voornamelijk geconcentreerd is onder een hoek van 30,64, en slechts zwakke energie wordt verdeeld over de andere twee hoeken. Voor eenvoudige observatie toont figuur 5c de faseverdeling van de meta-oppervlakconfiguratie bij de middelste golflengte. Uit figuur 5c kunnen we zien dat het doorgelaten licht duidelijk wordt gebroken en dat het golffront relatief vlak is. Door de werkgolflengte en de periode van de structuur in Vgl. (3) verkrijgen we een afwijkende transmissiehoek $\theta _r$ van 30,642, wat zeer dicht bij onze simulatieresultaten ligt. Om de relatie tussen het aantal diffractieorders en de verhouding van de golflengte tot de periode te verifiëren, stellen we $\lambda _0$/$P_x$ in op de kritische waarde van 0,5 en selecteren we vijf verschillende golflengten om theoretische berekeningen uit te voeren en FDTD-simulaties. De resultaten worden weergegeven in Tabel 2. Het is duidelijk dat de simulatieresultaten zeer consistent zijn met de berekende resultaten.

Volgens de berekende en gesimuleerde hoeken voor de voorgestelde structuur in tabel 2, wanneer $\lambda _0$/$P_x$ groter is dan 0,5, zijn alleen diffractieorde 0 en diffractieorde 1 aanwezig en is er geen diffractieorde 2. Wanneer $\lambda _0$/$P_x$ kleiner is dan 0,5, worden diffractieorders 0, 1 en 2 verkregen in de simulatie. Dit resultaat is volledig in overeenstemming met de hierboven beschreven theoretische analyse en bevestigt dus volledig de betrouwbaarheid van de gegeneraliseerde wet van Snell in combinatie met de roostertheorie.

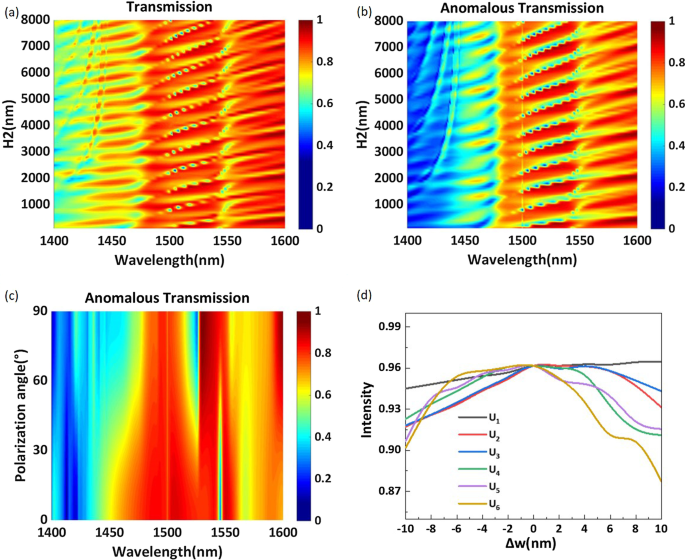
een De totale transmissie-efficiëntie en b de abnormale transmissie-efficiëntie als een functie van de substraatdikte voor het golflengtebereik van 1400-1600 nm. c De abnormale transmissie-efficiëntie van de voorgestelde structuur voor verschillende polarisatiehoeken in het golflengtebereik van 1400-1600 nm. d Berekend afwijkend transmissierendement bij verschillende waarden van de zijlengte w

In Fig. 6a, b is het golflengtebereik 1400-1600 nm, en de totale transmissie-efficiëntie en de abnormale transmissie-efficiëntie zijn uitgezet als een functie van de substraatdikte $H_2$. De transmissie-efficiëntie wordt beïnvloed door de substraatdikte en de piekgolflengte wordt roodverschoven met toenemende dikte. Het is duidelijk dat zowel de totale transmissie-efficiëntie als de abnormale transmissie-efficiëntie periodiek veranderen met toenemende substraatdikte. Om het geheugenverbruik in de computersimulatie te verminderen, wordt de geoptimaliseerde substraatdikte ingesteld op 7050 nm en bereikt de gewenste afwijkende transmissie-efficiëntie 96,2% bij een golflengte van 1529 nm. Wij zijn van mening dat een hoog afwijkend transmissierendement kan worden verkregen, zelfs als het substraat dik is. We berekenen ook de variatie in de afwijkende transmissie-efficiëntie met de polarisatiehoek van het invallende licht, zoals weergegeven in figuur 6c. Bij een golflengte van 1529 nm neemt de abnormale transmissie-efficiëntie toe met toenemende polarisatiehoek en bereikt een maximum wanneer de polarisatiehoek 90 is (y -polarisatie). Aangezien de lengte van de zijkant w van de structuur nauwkeurige numerieke waarden vereist en het moeilijk kan zijn om ze precies te fabriceren, berekenen we de abnormale transmissie-efficiëntie bij verschillende waarden van w om de tolerantie van de constructie te testen. Zoals weergegeven in Fig. 6d, wordt de tolerantie van de structuur verkregen door de lengte van de zijkant w te veranderen gebaseerd op de structurele parameters in tabel 1. Deze curven, $U_1$–$U_6$, vertegenwoordigen de variatie in de abnormale transmissie-efficiëntie met de zijlengtes van de zes nanostaafjes per periodiek interval. De horizontale as $\Delta w$ vertegenwoordigt het verschil tussen de gesimuleerde zijlengte en de zijlengte vermeld in Tabel 1. We kunnen zien dat curve $U_1$ erg vlak is en dat de abnormale transmissie-efficiëntie met slechts 2 verandert % met de zijlengte binnen een bandbreedte van 20 nm. De trends van de curven $U_2$,$U_3$, $U_4$ en $U_5$ zijn in principe hetzelfde, en een abnormale transmissie-efficiëntie van meer dan 90% kan worden verkregen wanneer de zijlengte binnen de 20 nm bandbreedte. Het is duidelijk dat het veranderen van de lengte van de zijde van $U_6$ de meest opvallende invloed heeft op de prestatie; niettemin vertoont $U_6$ nog steeds een hoge afwijkende transmissie-efficiëntie. Wanneer de zijlengte met 10 nm wordt verminderd, blijft het afwijkende transmissierendement boven 90%. Wanneer de zijlengte met 10 nm wordt vergroot, wordt de afwijkende transmissie-efficiëntie aanzienlijk beïnvloed, maar deze overschrijdt nog steeds 87%. Deze resultaten bewijzen dat een kleine fout tijdens de fabricage de prestaties van het meta-oppervlak niet wezenlijk beïnvloedt.

Het is te zien aan vgl. (3) dat de diffractiehoek van afwijkend transmissielicht wordt beïnvloed door $\lambda _0$/$P_x$; dus proberen we de grootte van $P_x$ te veranderen om verschillende afwijkende brekingshoeken te verkrijgen. Een effectieve methode om verschillende afwijkende brekingshoeken te realiseren is om het aantal elementen per periodiek interval te veranderen. Daarom ontwerpen we verder fase-gradiënt meta-oppervlakken met meerdere sets. De elementen van het meta-oppervlak veranderen per periodiek interval van drie naar negen. We selecteren de werkgolflengte met de hoogste afwijkende transmissie-efficiëntie voor elke groep meta-oppervlakken en observeren de faseverdeling van het doorgelaten licht. De simulatieresultaten zijn uitgezet in Fig. 7a-f. Naarmate het aantal elementen afneemt van negen naar drie, neemt de verhouding $\lambda _0$/$P_x$ geleidelijk toe en neemt de afwijkende transmissiehoek toe van 19,35 tot 68,58. Figuur 7a-f laat zien dat meta-oppervlakken met fasegradiënten met verschillende elementen bijna lineaire faseverdelingen kunnen realiseren en dat het golffront van het doorgelaten licht relatief glad is. We voeren verre veldanalyses uit van de bovenstaande configuraties en plotten de energieverdeling van doorgelaten licht langs elke diffractiehoek, zoals weergegeven in Fig. 8a-f. We kunnen meer dan 80% afwijkende transmissie-efficiëntie verkrijgen van 19,35 tot 46,68. De structurele parameters van elk element en gedetailleerde numerieke resultaten staan vermeld in Tabel 3. In ons optimalisatieproces is de zijdelengte van de regelmatige zeshoek w en de periode P zijn de belangrijkste optimalisatieparameters.

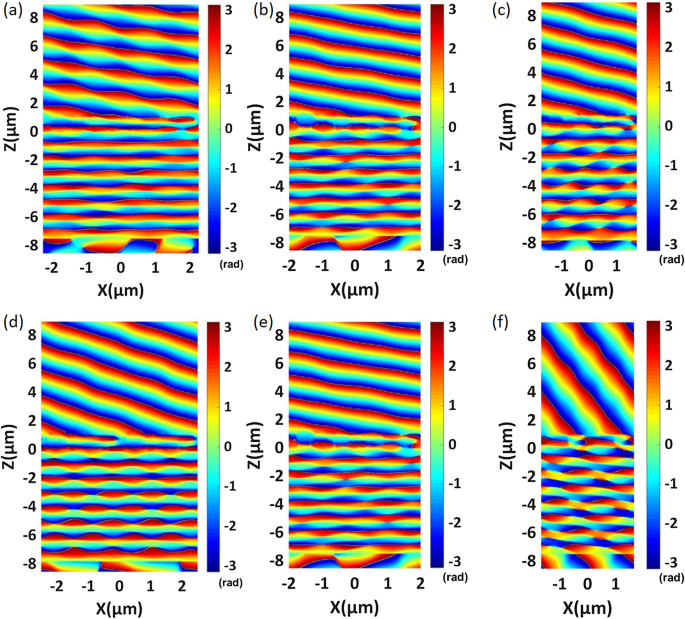
Faseverdeling van een fase-gradiënt meta-oppervlak bestaande uit verschillende elementnummers. een Meta-oppervlak met negen elementen. b Acht elementen meta-oppervlak. c Zeven elementen meta-oppervlak. d Meta-oppervlak met vijf elementen. e Meta-oppervlak met vier elementen. v Meta-oppervlak met drie elementen. d –f geef twee perioden weer om het afwijkende transmissie-effect beter weer te geven. De gedetailleerde parameters worden weergegeven in Tabel 3

Transmissie-intensiteiten in het verre veld onder verschillende hoeken van meta-oppervlakken met fasegradiënt bestaande uit verschillende elementnummers. een –f vertegenwoordigen respectievelijk negen, acht, zeven, vijf, vier en drie elementen

een Gesimuleerde fasevariatie van het meta-oppervlak met grote hoek langs de x -richting in een volledige periode voor golflengten van 1400-1600 nm. b Volledige $2\pi$ faseverschuiving langs de x -richting van het fase-gradiënt meta-oppervlak voor 1450, 1500, 1536 en 1550 nm. c De intensiteit van de totale transmissie en abnormale transmissie

According to the generalized Snell’s Law, to design a larger anomalous refraction angle $\theta _r$, we should increase the ratio of the working wavelength $\lambda$ to the structural period $P_x$. As shown in Fig. 9a, we plot the phase variation of the transmitted light along the x -direction for wavelengths of 1400–1600 nm. For clarity, we select four wavelength points, i.e., 1450 nm, 1500 nm, the central working wavelength 1536 nm, and 1550 nm, to plot the phase shift curves shown in Fig. 9b. It is clear that the all-dielectric metasurface can realize a full $2\pi$ phase shift for the wavelength points. From Fig. 9b, we can see that the phase variation shows a linear trend along the x -direction. We calculate the total transmission efficiency and the desired anomalous transmission efficiency of the structure in the working band, the results of which are shown in Fig. 9c. It can be observed that the total transmission efficiency is lower than before. However, at the operating wavelength of 1536 nm, the anomalous transmission efficiency can reach 69.6% with an anomalous refraction angle of 68.58. The phase distribution of transmitted light and the energy distributions at different anomalous refraction angles are shown in Figs. 7f and 8f, respectively. From the electric field distribution, we can clearly see that the equilateral phase plane of the transmitted light is very flat. The transmitted light emits very little energy at 0 and $-68.58$, and the majority of transmitted light is concentrated at 68.58. The anomalous transmission performance of the all-dielectric phase-gradient metasurface designed by us is better than that of most of the metasurface structures proposed before, and the anomalous transmission efficiency can reach more than 60% within the range of anomalous refraction angles from 0 to 70. Based on the above analysis, an anomalous refraction angle of approximately 30 is the most reasonable. At this anomalous refraction angle, the highest anomalous transmission efficiency can be achieved, and the anomalous refraction angle can be guaranteed to be large enough.

Conclusies

In summary, we designed and numerically investigated an all-dielectric phase-gradient metasurface to achieve high-efficiency anomalous transmission in the near-infrared region. The metasurface consists of regular hexagonal silicon nanorods arranged on a silica substrate. The FDTD method was used to calculate the transmission efficiency and anomalous refraction angle of the transmitted light. The results show that the metasurface can realize a complete $2\pi$ phase shift in the wavelength range of 1400–1600 nm. At a center wavelength of 1529 nm, the desired anomalous transmission efficiency reached 96.2% with an anomalous refraction angle of 30.64. Furthermore, the anomalous transmission efficiency exceeded 80% in the range of 1527–1545 nm, which means that our design is more flexible. We also designed multiple sets of phase-gradient metasurfaces by changing the number of elements per periodic interval and adjusting the period of the metasurface. The optimized results show that we can modulate the anomalous refraction angle in the range of 19.35-68.58. When the anomalous refraction angle is less than 46.68, more than 80% of the anomalous transmission efficiency can be obtained. Such an all-dielectric metasurface will be easy to apply to integrated optical devices.

Beschikbaarheid van gegevens en materialen

The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.

Afkortingen

FDTD:: Finite difference time domain
TE:: Transverse electric
LPCVD:: Low-pressure chemical vapor deposition
EBL:: Elektronenbundellithografie
PEC:: Proximity effect correction
EME:: Electromagnetic multipole expansion
SCSs:: Scattering cross sections
ED:: Electric dipole
MD:: Magnetic dipole
EQ:: Electric quadrupole
MQ:: Magnetic quadrupole

Impact van oppervlaktetoestanden en aluminiummolfractie op oppervlaktepotentiaal en 2DEG in AlGaN/GaN HEMT's Volledige Terahertz-polarisatiecontrole met verbrede bandbreedte via diëlektrische metasurfaces

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal