Magische wiskundige formules voor nanoboxen

Omdat we naaste buur-nabijheidsmatrices maken, kennen we het coördinatiegetal \(\hbox {cn}_i\) van hoekpunt i door de elementen van \({{\mathbf{A}}}(i,:)\) op te tellen. Onze structuur bestaat uit \(n+1\) shells genummerd 0, 1, ..., n , met t buitenste lagen. Zij \(N_{{\rm cn}_i}(n,t)\) het aantal atomen met coördinatie \(\hbox {cn}_i\) waarbij \(1\le \hbox{cn}_i\le \hbox{cn}_M\) met \(\hbox {cn}_M\) de maximale coördinatie in de nanobox. Dan wordt het totale aantal atomen in de nanobox gegeven door

De oppervlakte-atomen in de buitenste schil (of binnenkant) van de nanobox, n een set bindingen hebben die kleiner is dan de bulkcoördinatie. Dus de maximale coördinatie voor oppervlakte-atomen is \(\hbox {cn}_s <\hbox{cn}_M\), en het aantal oppervlakte-atomen is

Dit geldt als alle niet-oppervlaktehoekpunten een grotere coördinatie hebben dan \(\hbox {cn}_s\), wat geldt voor alle fcc-, bcc- en hcp-clusters. We bepalen de \(N_{{\rm cn}_i}(n,t)\) door de kolommen van de aangrenzende matrix te tellen waarvan de som \(\hbox {cn}_i\) is. Merk op dat ons clustercoördinaatalgoritme is gebouwd door shells, zodat elke volgende shell alle eerdere lagere waarden van n bevat. . Bovendien is het aantal obligaties in de doos

waarbij \(N_{{\rm B}}(n,t)\) het aantal bindingen is en \(\hbox {cn}_M\) de maximale coördinatie is. De factor 1/2 komt tot stand vanwege de paarsgewijze dichtstbijzijnde buurbinding.

Omdat we weten dat deze vergelijkingen afhankelijk zijn van n , t als polynoom van graad 3 kunnen we \(N_{{\rm cn}_i}(n,t)\) berekenen voor 4 opeenvolgende waarden van n , zeg \(n=n_0+j\), j = 0, 1, 2, 3. Een eenvoudig interpolerend polynoom geeft dan de polynoomcoëfficiënten. Er moet worden geverifieerd dat door het verhogen van \(n_0\), wat meestal gelijk is aan 1, de formules niet veranderen. Als de formules vanaf \(n_0\) stabiel worden, dan gelden ze voor alle \(n\ge n_0\). Om de exacte rationale coëfficiënten te krijgen, moet men het Vandermonde-systeem voor de coëfficiënten in exacte rekenkunde oplossen.

Merk op dat we in de magische formules voor nanoboxen dat \(n> t\) hebben zodat daarom tegen elke verwachting de box wordt gevuld door een passende keuze van t zal de originele magische formules voor de volledige solide clusters niet opnieuw creëren. Deze magische formules zijn handig voor het modelleren van de mesoschaaleigenschappen van clusters en dozen of kooien. Complete sets formules zijn oorspronkelijk afgeleid voor negentien clustertypen. In dit manuscript leiden we magische formules af voor dertien soorten nanoboxen.

In de onderstaande magische formules zien we dat bulkcoördinatie kan voorkomen voor t = 2 of t =3 lagen schaaldikte. De meeste zijn voor lagen waar t = 2; de uitzonderingen zijn de fcc-kubus, de cuboctaëder, de icosaëder en de bcc-kubus en de afgeknotte kubus. In het laatste geval verschijnt bulkcoördinatie alleen voor t = 3 lagen. Voor de onderstaande gegevens zijn de tabellen van de magische formules vergezeld van een figuur van een 'halve doos' om het interieur van de nanoboxen te laten zien. Hiernaast is een kleurenbalk die de coördinatie en het aantal ervan tussen haakjes aangeeft.

Resultaten en discussie

Om de toepasbaarheid van magische formules af te bakenen, schetsen we hoe katalytisch gedrag kan afhangen van coördinatie en dergelijke formules. We definiëren G als de grootteafhankelijke Gibbs-energie van het cluster. Omdat adatomen aan de buitenste schilatomen zijn gebonden, is er een toename van G dat heet de adsorptie-energie en wordt aangeduid als \(\Delta G\). Dit kan worden opgesplitst over verschillende coördinatietypen van de atomen op de buitenste schil die zich aan adatoms hechten. Een knikatoom voegt bijvoorbeeld een hoeveelheid \(\Delta G_{k}\) toe aan de adsorptie-energie. Evenzo voegt een randatoom \(\Delta G_{e}\) toe, terwijl een facetatoom \(\Delta G_f\) dan [18] bijdraagt:

$$\Delta G=\sum _{o\in \{f,e,k\}} \Delta G_o N_o$$ (7)

waarbij \(N_o\) het aantal atomen in de buitenste schil van het aangegeven type is. Het totale aantal atomen in de buitenste schil gebonden aan adatoms wordt gedefinieerd als \(N_s=N_f+N_e+N_k\), wat resulteert in:

$$\begin{aligned}\Delta G=&{} \Delta G_f\cdot (1-f_e-f_k)+\Delta G_e\cdot f_e+\Delta G_k\cdot f_k \\&\quad {\hbox{where} } \,\,f_o=N_o/N_s, \,\,o\in \{e,k\},\end{uitgelijnd}$$ (8)

met de Gibbs-energiefractie uitgedrukt door de rand- en kniklocaties die expliciete coördinatie hebben voor specifieke structuren. Dit toont aan dat magische formules een rol spelen bij oppervlaktereacties, via rand- en knikcoördinaties en hun formules. Merk op dat vgl. (8) is van toepassing op adsorptie aan on-top sites, anders zullen niet alle adatomen worden gebonden aan atomen in de buitenste schil. In zo'n model hebben de kniksites magische formules die constant zijn met het aantal schelpen, n , edge-sites hebben formules die lineair zijn met n , en facetsites hebben formules die kwadratisch zijn met n . Meer specifiek zijn de kniksites de laagste gecoördineerde formules, de edge-sites de op één na laagste gecoördineerde en facetsites hebben cn = 8 voor (100) facetten en cn = 9 voor (111) facetten.

Per deeltje kunnen twee fundamentele relaties worden toegepast. Voor de Gibbs-energie en adsorptieconstante, \(K_{{\rm a}}\), geldt:

$$K_{{\rm a}}={\exp } \left( -\frac{\Delta G}{RT}\right) ,$$ (9)

waar R is de gasconstante en T is de temperatuur in Kelvin. Bovendien worden Brønsted-Evans-Polanyi-relaties veel gebruikt in homogene en heterogene katalyse [18, 22] met behulp van een relatie voor reactieconstanten k en evenwichtsconstanten K als volgt:

$$k=gK^{\alpha },\quad 0<\alpha <1,$$ (10)

waar g en \(\alpha\) (Polanyi-parameter) zijn constanten. De Polanyi-parameter is eenheidsloos en een echte breuk, zoals oorspronkelijk gegeven door Brønsted [23]. We hebben dan:

$$k=k'_{a}{\exp } \Bigl (-\alpha \bigl ({f_n^{e}\cdot \chi _{_e}({D_n}) +f_n^{k}\cdot \chi _{_k}({D_n})}\bigr )\Grote ),$$ (11)

waar

$$\begin{aligned} &\chi _{_e}(D)=\frac{\Delta G_e(D)-\Delta G_f(D)}{RT},\\&\chi _{_k}(D )=\frac{\Delta G_k(D)-\Delta G_f(D)}{RT}, \end{uitgelijnd}$$ (12)

en

$$k'_{a}=g\exp \left( -\alpha \frac{\Delta G_f}{RT}\right) .$$ (13)

Deze analyse laat zien dat voor het bepalen van een katalytisch model een methode nodig is om de Gibbs-energie te berekenen. Bekende katalytische reacties zoals de tweestaps- en Langmuir-Hinshelwood-mechanismen zijn overwogen [24].

FCC-nanoboxen

Gezichtsgecentreerde kubische structuren zijn de meest voorkomende vorm voor nanoclusters en nanoboxen. Dit is de structuur van de metalen met interessante eigenschappen, zoals de edele metalen met plasmonische eigenschappen, en de katalytische edelmetalen. Omdat goud een hoog reductiepotentieel heeft van 1,50 V (zie vergelijking 1) in vergelijking met de standaard waterstofelektrode (SHE) [5], is het een van de gemakkelijkst te synthetiseren metalen als nanobox of nanocage. Er zijn gouden nanodozen of nanokooien gevormd in de vorm kubieke [1], kuboctahedron [25], icosaëder en decaëder [26], octaëder [27] en tetraëder [28].

We kunnen de geschatte grootte van deze nanoboxen bepalen door een coördinatiebenadering te gebruiken voor de bindingslengte van de dichtstbijzijnde buur r (cn) [29],

$$r(cn) =\frac{2r_{{\rm B}}}{\left( 1+\exp \left( \frac{12 - \langle cn \rangle _c)}{8\cdot \langle cn \rangle _c}\right) \right) }.$$ (14)

Hierin is \(r_{{\rm B}}\) de lengte van de bulkbinding voor goud (0,2884 nm) en is \(\langle cn \rangle _c\) de gemiddelde coördinatie van het cluster. We vinden een lineair verband tussen D en n , het aantal clustershells, zoals weergegeven in Tabel 1:

$$D(n)=a \cdot r_{{\rm B}} \cdot n + b.$$ (15)

We gebruiken nanoboxen met t = 3, aangezien de formules variëren met t , en we willen wat bulkcoördinatie bereiken. Voor de berekening van D (n ), gebruiken we de maximale afstand tussen atomen in het cluster, afgeleid van de Euclidische matrix. Merk op dat D (n ) is een empirische formule, afgeleid van gegevens (variëren n en bereken D ), en is als zodanig niet bewezen.

Deze relaties produceren diameters in overeenstemming met andere gegevens, uit DFT. Voor de massieve cuboctaëders met N gelijk aan 55, 561 en 923 krijgen we diameters van 1,12 nm, 2,85 nm en 3,43 nm. Dit steekt gunstig af bij gepubliceerde DFT-resultaten voor 55 atomen van 1,1 nm [30], voor 561 atomen, 2,7 nm [31] en voor 923 atomen, 3,5 nm [30]. De magische formules voor sommige fcc-nanoboxen zijn hieronder weergegeven (tabellen 2, 3, 4, 5, 6, 7, 8).

Icosahedrale en Decahedral Nanoboxes

Zie tabellen 9 en 10.

Diamond en Simple Cubic Nanoboxes

De diamant kubische roosterstructuur wordt gevormd door een allotroop van koolstof en de elementen silicium en germanium. Ook vormen sommige kubische verbindingen deze structuur, zoals kubisch ijzeroxide, tetraëdrische diamantmaghemiet \(\gamma\)-Fe₂ O₃ . De bindingslengte voor Fe–O in tetraëdrische diamantmaghemiet \(\gamma\)-Fe₂ O₃ =0,186 nm [32]. Dit leidt tot de diameter van diamantclusters D (n ) zoals hieronder:

$$D(n) =3.3984\cdot n_{{\rm B}} \cdot n - 0.21194.$$ (16)

Volgens referentie [12] werden microboxen van kubisch ijzeroxide gevormd en hadden ze interessante lithiumopslagmogelijkheden. We zijn niet op de hoogte van een volledig coördinatiemodel voor energieopslag, maar zoals hierboven vermeld, geven DFT-resultaten aan dat activiteit kan afhangen van facetoriëntatie [19]. Een dergelijk model van opslagafhankelijkheid van coördinatie bestaat momenteel niet zoals we hebben voor katalyse. Uit vergelijking (16) hierboven (gemaakt met t = 4), een microbox vereist ongeveer n =1600 schelpen voor diamantmaghemiet. Magische formules voor de diamant en eenvoudige kubische roosterstructuren worden hieronder vermeld (tabellen 11, 12).

BCC Nanoboxen

Zie tabellen 13, 14 en 15.

HCP-nanoboxen

Zie tabel 16.

De zaak t = 1

Het speciale geval t = 1 is uniek en heeft als zodanig verschillende magische formules. We onderzoeken dit geval voor enkele van de bovenstaande nanoboxen. Nanoboxen met ultradunne wanden zijn gevormd met kubische [33], octaëdrische [16] en icosaëdrische vormen [34]. Volgens onderstaande magische formules is de kubieke nanobox met t = 1 heeft de laagste coördinatie. Platina heeft een relatief hoog reductiepotentieel van 1,18 V ten opzichte van de SHE, dus het kan worden gevormd door galvanische vervanging, zie Vgl. (1) [5]. De eigenschappen van de oxidatiereductiereactie (ORR) van sommige van deze op platina gebaseerde nanokooien geven echter aan dat structuren met (111) facetten in tegenstelling tot (100) facetten betere ORR-massa-activiteiten hebben [35].

Zo heeft de icosaëder met 20 (111) facetten de beste ORR-massaactiviteit, gevolgd door de octaëder en als laatste de afgeknotte kubus. Deze eigenschap van katalytisch gedrag waarbij de facetoriëntatie voorrang heeft op het coördinatiegetal, blijkt uit de onderstaande tabelgegevens. Met andere woorden, zoals vermeld in de volgende tabellen, heeft de kubus met (100) facetten de laagste magische coördinatiegetallen met vier en vijf, maar de octaëder en icosaëder met (111) facetten en grotere magische formules hebben een betere ORR-activiteit. Deze eigenschap wordt ook aangetoond in nanoclusters, waar DFT-resultaten de dominantie van de (111) facetten [36] bevestigen, vooral voor PtNi-legeringen (tabellen 17, 18, 19, 20, 21).

Verspreiding

Gezien het belang van rand- en knikplaatsen ten opzichte van facetten met betrekking tot katalytische activiteit, hebben we de oppervlaktedispersie bepaald voor sommige van de nanoboxen die we bestuderen. De (100) facetten hebben cn =8 terwijl de (111) facetten cn =9 hebben. Dit kan inzicht geven in de redenen voor de individuele polyedrische activiteit in vergelijking met de nanoboxen. In Fig. 1 hieronder plotten we de oppervlaktedispersie \(D_{{\rm s}} =(N_{{\rm e}} + N_{{\rm k}}) / N_{{\rm S}} \cdot 100\%\). In deze relatie is \(N_{{\rm k}}\) het aantal knik- of hoeksites en \(N_{{\rm e}}\) het aantal edge-sites. Zoals te zien is in figuur 1 hebben nanoboxen met (111) oppervlakken in tegenstelling tot (100) oppervlakken een hogere dispersie, waardoor de voorkeur van de katalytische activiteit van het (111) facet geloofwaardig wordt.

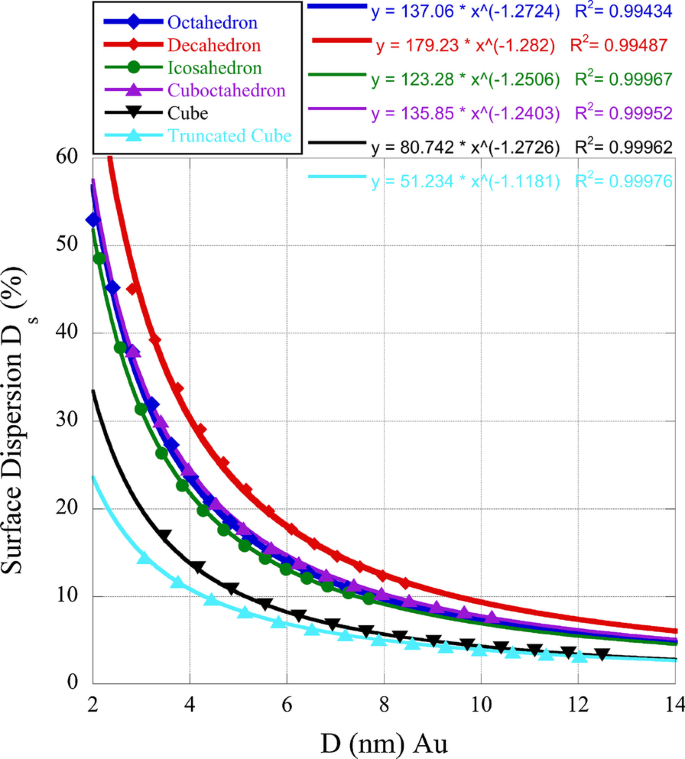
Oppervlaktedispersie van gouden nanoboxen

Conclusie

Samenvattend hebben we de eerste gedetailleerde wiskundige beschrijving van magische formules voor nanoboxen gepresenteerd. Het geval van de schaaldikte, t = 1 verschilt van \(t>1\) en voor sommige van deze gevallen brengen we de gegevens in een tabel. De formules voor de coördinatie, het aantal atomen en het aantal bindingen worden allemaal opgesomd. We zien dat bulkcoördinatie verschijnt voor lagen waar t =2 of 3, en is als zodanig veel dunner dan normaal gesynthetiseerd. De voordelen van lage coördinatie worden alleen bereikt voor zeer dunne wanden. We verwachten dat deze resultaten nuttig zullen zijn voor modellering en experimenteel werk.

Beschikbaarheid van gegevens en materialen

De dataset(s) die de conclusies van dit artikel ondersteunen, zijn verkrijgbaar bij de corresponderende auteur.

Afkortingen

bcc:

Lichaam gecentreerd kubisch

fcc:

Gezicht gecentreerd kubisch

hcp:

Zeshoekig dicht verpakt

DFT:

Dichtheidsfunctionaaltheorie

ZIJ:

Secundaire waterstofelektrode