Theoretisch systeem van contact-mode tribo-elektrische nanogeneratoren voor een hoge energieconversie-efficiëntie
Abstract
Door de snelle uitbreiding van de elektronica van de volgende generatie zijn draagbare en efficiënte energiebronnen een van de belangrijkste factoren geworden die de marktontwikkeling belemmeren. Tribo-elektrische nanogeneratoren (TENG's) zijn een potentiële kandidaat vanwege zijn onovertroffen eigenschappen. Hierin hebben we het vermogen en de conversie-efficiëntie van TENG's met contactmodus grondig geanalyseerd, rekening houdend met het hele energieconversieproces. Ten eerste, die verder ging dan de conventionele analyse, werd een compressiekracht geïntroduceerd om een veelzijdiger bewegingsprofiel af te leiden, wat een beter begrip opleverde van het werkingsprincipe van het contactscheidingsproces. Vervolgens hebben we de invloed van verschillende parameters op de prestaties grondig geanalyseerd. Vooral de maximale efficiëntie TENG's kunnen worden verkregen onder optimale kracht. Het is realistisch en nuttig voor efficiëntere TENG's. Bovendien maakt dit onderzoek een goede kans om normen vast te stellen voor het kwantificeren van de efficiëntie van TENG's, wat de basis legt voor de verdere industrialisatie en multifunctionaliteit van TENG's-technologie.
Achtergrond
De kunstmatige intelligentie en het cloudnetwerk verbeteren geleidelijk de kwaliteit van ons moderne leven met de snelle ontwikkeling van de volgende generatie elektronica voor smart home, gezondheidsmonitoring, entertainment en omgevingsmonitoring [1,2,3]. Het voeden van deze grote hoeveelheden elektronica is een onmogelijke missie geworden door gebruik te maken van bestaande batterijtechnologieën, gezien de grote omvang, korte levensduur en vooral snellaadproblemen. Het is een van de belangrijkste belemmeringen geworden om een duurzame stroombron te ontwikkelen die geschikt is voor draagbare elektronica [4,5,6].
Momenteel is aangetoond dat tribo-elektrische nanogeneratoren (TENG's) op basis van tribo-elektrificatie een aantrekkelijke technologie zijn voor het oogsten van mechanische energie. Het is een veelbelovende kandidaat voor draagbare elektronica vanwege de talrijke voordelen, waaronder flexibiliteit [7], kosteneffectiviteit [8], eenvoudig fabricageproces [9], milieubescherming [10] en veelzijdigheid [11]. Het is op grote schaal gebruikt om energie te oogsten uit mechanische omgevingsenergie. Bovendien kan het worden gebruikt om te integreren met draagbare apparaten voor zelfaangedreven toepassingen [12,13,14]. Voorlopig zijn er veel methoden gebruikt om het vermogen te vergroten, waaronder oppervlaktemorfologie [15, 16], materiaaloptimalisatie [17, 18], ladingsinjectie [19, 20], structuuroptimalisatie [21, 22] en multi-nanogeneratoren [23, 24]. Ondanks de snelle vooruitgang in outputprestaties, ontbreekt een definitief model voor het analyseren van de energieconversie-efficiëntie. Er zijn een aantal theoretische verklaringen gepubliceerd voor verschillende modi van TENG's [25,26,27]. De meeste analyses bespreken echter niet het hele energieconversieproces en richten zich alleen op het uitgangsvermogen. Wat nog belangrijker is, een hoger uitgangsvermogen betekent niet een hogere energieconversie-efficiëntie en kan zelfs contraproductief blijken te zijn. Het heeft de ontwikkeling van efficiëntere TENG's enigszins belemmerd vanwege een gebrek aan direct onderzoek naar de efficiëntie van energieconversie.
In dit werk hebben we systemisch en direct de kracht en conversie-efficiëntie van TENG's met contactmodus geanalyseerd, rekening houdend met het hele proces. Ten eerste, die verder ging dan de conventionele analyse, werd een compressiekracht geïntroduceerd om een veelzijdiger bewegingsprofiel af te leiden, wat een beter begrip opleverde van het werkingsprincipe van het contactscheidingsproces. Vervolgens werden, volgens de bewegingsvergelijkingen, expliciete vergelijkingen voor de belangrijke apparaatprestaties in het hele contact- en scheidingsproces gepresenteerd. Ten slotte werd de invloed van materiaaleigenschappen, structurele parameters en experimentele factor op het maximale vermogen en vooral de energieconversie-efficiëntie systematisch onderzocht. We kunnen de maximale efficiëntie en kracht verkrijgen door rationeel parameters te ontwerpen, met name de drukkracht. Het is realistisch en nuttig voor efficiëntere TENG's. Belangrijk is dat het een goede kans maakt om de normen vast te stellen voor het kwantificeren van de efficiëntie van TENG's, wat de basis legt voor de verdere industrialisatie en multifunctionaliteit van TENG's.
Methoden
Het basiswerkingsprincipe van TENG's is gebaseerd op tribo-elektrificatie en elektrostatische inductie. Het zou met het oog op de wrijvingsmaterialen bij benadering in twee typen kunnen worden ingedeeld. Vanwege de werkfunctie en wrijving worden het diëlektrische materiaal en het geleidermateriaal gekozen als de tribo-elektrische paren. Zoals weergegeven in Fig. 1 bestaat de bovenste laag uit de bovenste elektrode (TE) en de diëlektrische laag kan op en neer bewegen, terwijl de onderste elektrode (BE) op het substraat is bevestigd. De twee lagen zijn verbonden met een belastingsweerstand R . Het scheidings- en contactproces zijn aangegeven in respectievelijk Fig. la, b. In het scheidingsproces stromen elektronen van de TE naar de BE en keren ze terug naar de TE in het contactproces.
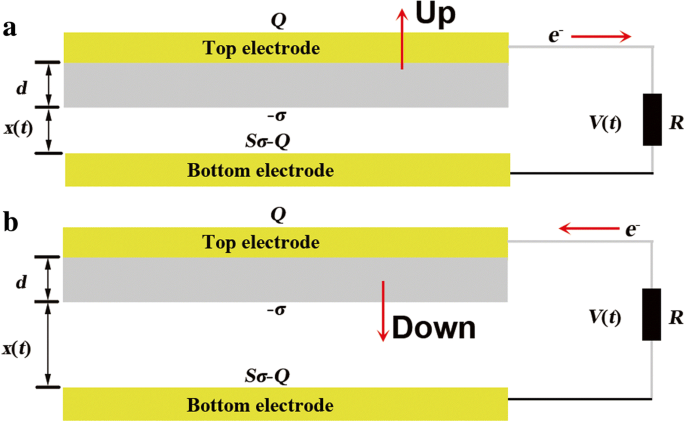
Het theoretische model voor de contactmodus van TENGA's. een Scheidingsproces en b contactproces
Onder de uitgeoefende kracht F , zal de bovenste laag volledig contact maken met de onderste laag. De BE zal positieve tribo-elektrische ladingen hebben met de oppervlakteladingsdichtheid σ terwijl de diëlektrische laag dezelfde ladingen heeft met tegengesteld teken. In het scheidingsproces scheidt de bovenste laag met de onderste laag met een afstand x (t ). Het zal resulteren in een potentiaalverschil V (t ) tussen de TE en BE vanwege het elektrische veld. Om V . te compenseren (t ), zullen elektronen tussen de twee elektroden stromen door R . Daarom is de lading van de TE Q terwijl de BE blijft staan met Sσ − V . De elektrische veldsterkte in de twee regio's wordt als volgt gegeven volgens de stelling van Gauss.
Binnen de diëlektrische laag:
$$ {E}_{\mathrm{dielectric}}=-\frac{Q}{S{\varepsilon}_0{\varepsilon}_r} $$ (1)In de luchtspleet:
$$ {E}_{\mathrm{air}}=\frac{\sigma_0-Q/S}{\varepsilon_0} $$ (2)waar ε 0 en ε r zijn respectievelijk de vacuümdiëlektrische en de relatieve permittiviteit.
De V (t ) moet aan de volgende vergelijking voldoen:
$$ V(t)={E}_{\mathrm{dielectric}}d+{E}_{\mathrm{air}}x(t) $$ (3)Van de wet van Ohm, de V (t ) wordt gegeven als
$$ V(t)=RI(t)=R\frac{dQ}{dt} $$ (4)Door vergelijkingen samen te voegen, kunnen we
$$ \frac{dQ}{dt}+\frac{d_0+x(t)}{RS{\varepsilon}_0}\times Q=\frac{\sigma x(t)}{R{\varepsilon}_0 } $$ (5)De vergelijking (5) is de regerende vergelijking van TENG's. Het kan worden toegepast op het hele scheidings- en contactproces. Het is duidelijk dat x (t ) is een van de belangrijkste factoren van TENG's. In tegenstelling tot eerder werk, bouwen we de praktische bewegingsvergelijking in plaats van deze rechtstreeks aan te nemen. In dit artikel is de bewegingsvergelijking in het hele proces gebaseerd op de drukkracht en de experimentele conditie.
Resultaten en discussie
Niet-veersysteem
Ten eerste beschouwen we alleen een constante drukkracht F en de zwaartekracht van de toplaag. De bewegingsvergelijking kan als volgt worden verkregen (zie aanvullend bestand 1:opmerking 1 en afbeelding S1 in de ESM). In werkelijkheid is de x (t ) heeft altijd een maximale waarde x max en minimaal nul. Dus de bewegingsvergelijkingen worden gegeven door
$$ \left\{\begin{array}{c}\ x(t)=\frac{F- mg}{2m}{t}^2,t<\sqrt{\frac{2{x}_{ \mathrm{max}}m}{F- mg}}\ \\ {}x(t)={x}_{\mathrm{max}},t\ge \sqrt{\frac{2{x}_ {\mathrm{max}}m}{F- mg}}\end{array}\right. $$ (6.1) $$ \left\{\begin{array}{c}\ x(t)=\frac{F+ mg}{2m}{t}^2,t<\sqrt{\frac{2{ x}_{\mathrm{max}}m}{F+ mg}}\ \\ {}x(t)=0,t\ge \sqrt{\frac{2{x}_{\mathrm{max}} m}{F+ mg}}\end{array}\rechts. $$ (6,2)De vergelijkingen. (6.1) en (6.2) vertegenwoordigen respectievelijk het scheidingsproces en het contactproces.
Dan kunnen we de overgedragen kosten krijgen. (De gedetailleerde afleiding staat in aanvullend bestand 1:noot 2 in de ESM).
In het scheidingsproces:
$$ {\displaystyle \begin{array}{l}Q(t)=\exp \left(-\frac{6m{d}_0t+\left(F- mg\right){t}^3}{6 mRS {\varepsilon}_0}\right)\\ {}\times {\int}_0^t\frac{\sigma \left(F- mg\right){t}^2}{2 mR{\varepsilon}_0 }\mathit{\exp}\frac{6m{d}_0t+\left(F- mg\right){t}^3}{6 mRS{\varepsilon}_0} dt,t<\sqrt{\frac{2 {x}_{\mathrm{max}}m}{F- mg}}\end{array}} $$ (7.1) $$ {\displaystyle \begin{array}{l}Q(t)=\frac {\sigma S{x}_{\mathrm{max}}}{d_0+{x}_{\mathrm{max}}}-\left(\frac{\sigma S{x}_{\mathrm{max} }}{d_0+{x}_{\mathrm{max}}}-{Q}_0\right)\\ {}\times \mathit{\exp}\left(-\frac{d_0+{x}_{\ mathrm{max}}}{RS{\varepsilon}_0}\left(t-{t}_0\right)\right),t\ge \sqrt{\frac{2{x}_{\mathrm{max} }m}{F- mg}}\end{array}} $$ (7,2)waarbij \( {t}_0=\sqrt{2{x}_{\mathrm{max}}m/\left(F- mg\right)} \), en Q 0 = Q (t 0 ) in vgl. (7.1).
In het contactproces:
$$ {\displaystyle \begin{array}{l}Q(t)=\exp \left(-\frac{6m{d}_0t+\left(F+ mg\right){t}^3}{6 mRS{ \varepsilon}_0}\right)\\ {}\times \left(\sigma S+{\int}_0^t\frac{\sigma \left(F+ mg\right){t}^2}{2 mR{ \varepsilon}_0}\mathit{\exp}\frac{6m{d}_0t+\left(F+ mg\right){t}^3}{6 mRS{\varepsilon}_0} dt\right),t<\ sqrt{\frac{2{x}_{\mathrm{max}}m}{F+ mg}}\end{array}} $$ (8.1) $$ Q(t)={Q}_0\times \exp \left(\frac{d_0{t}_0-{d}_0t}{RS{\varepsilon}_0}\right),t\ge \sqrt{\frac{2{x}_{\mathrm{max}} m}{F+ mg}} $$ (8,2)waarbij \( {t}_0=\sqrt{2{x}_{\mathrm{max}}m/\left(F+ mg\right)} \), Q 0 kan worden berekend door t . toe te wijzen = t 0 in Verg. (8.1).
Daarom kan de uitgangsstroom worden afgeleid als I (t ) = dQ /dt en V (t ) = RI (t ).
Volgens de specifieke parameters weergegeven in Tabel 1 kunnen we de numerieke berekeningsresultaten verkrijgen.
De relatie tussen kenmerken en tijd bij verschillende R in het hele proces wordt weergegeven in Fig. 2. De overgedragen ladingen, uitgangsstroom en uitgangsspanningsrelaties bij verschillende belastingen in het contactproces worden getoond in Fig. 2a, c, e. Het gedrag is vergelijkbaar met de eerdere onderzoeken [25]. Maar het scheidingsproces wordt zelden bestudeerd. Neem aan dat de oppervlakteladingen na een lange tijd volledig worden overgedragen op de TE in het scheidingsproces. Zoals getoond in figuur 2b, kunnen de ladingen in de TE bij kortsluiting (SC) volledig terugvloeien naar de BE wanneer de bovenste laag stopt met bewegen (t = 2 ms). De kosten kunnen niet dalen tot nul bij t = 2 ms wanneer R is meer dan 1 MΩ. Terwijl bijna alle kosten worden overgedragen aan de BE wanneer R minder is dan 10 MΩ in het scheidingsproces. De overgedragen ladingen in het contactproces zijn veel minder dan het scheidingsproces. Dit heeft te maken met de relatief kleine drijvende kracht in het vroege contactproces. De uitgangsstroom-tijdrelatie is uitgezet in figuur 2d. Bij SC-conditie is de piekstroom bijna hetzelfde als in het scheidingsproces. Wanneer R groter is, heeft de huidige-tijdcurve twee lokale maximale waarden, namelijk aan het begin en het einde van de beweging. En de absolute maximale stroom daalt dramatisch naarmate de weerstand toeneemt. De twee lokale maximale waarden aan het begin en het einde van de beweging zijn respectievelijk het gevolg van de adequate elektronen en de snelle beweging. De uitgangsspanning heeft hetzelfde profiel met de stroom, maar een andere trend in grootte, zoals weergegeven in figuur 2f (zie aanvullend bestand 1:figuur S2 voor de gedetailleerde relatie in de ESM). Opgemerkt moet worden dat de absolute maximale spanningswaarde veel kleiner is in vergelijking met die in het scheidingsproces. Het is duidelijk dat de spanning en stroom niet symmetrisch zijn in het scheidings- en contactproces. Door het scheidings- en contactproces te combineren, wisselen de uitgangsspanning en stroom elkaar af.
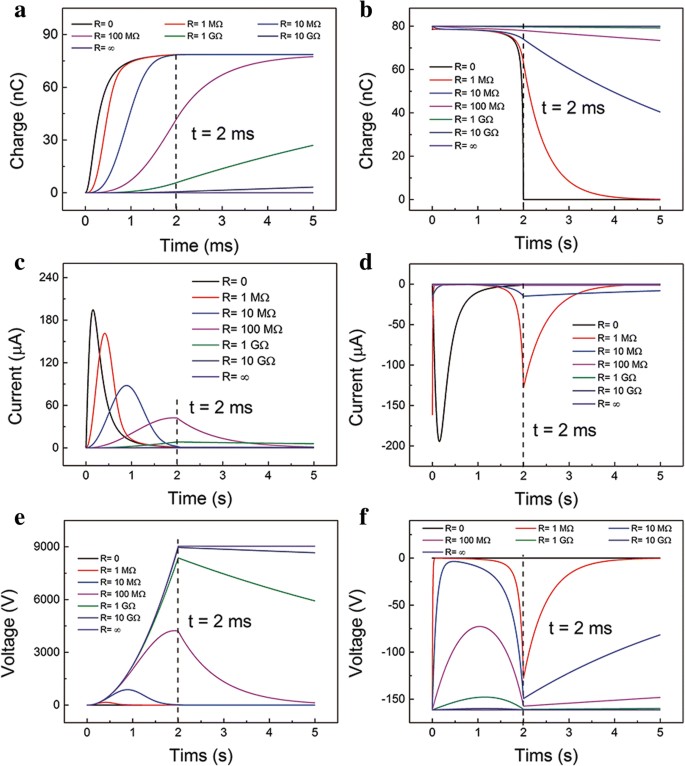
Berekende uitgangskarakteristieken wanneer het apparaat onder een constante drukkracht staat F. Overgedragen kosten-tijd relatie bij verschillende R in de a contactproces en b scheidingsproces. Huidige-tijd relatie op verschillende R in de c contactproces en d scheidingsproces. Spanning-tijdrelatie bij verschillende R in de e contactproces en f scheidingsproces
Daarnaast is de invloed van verschillende parameters op de relatie tussen maximaal vermogen P max en de bijbehorende weerstand zijn uitgezet in Fig. 3. Deze verschillende parameters kunnen worden onderverdeeld in materiaal, structuur en experimentconditie. De materiaalparameters omvatten bijvoorbeeld de σ en ε r . De structurele parameters zijn voornamelijk oppervlaktegrootte S, x max en d. De drukkracht F is een experimentparameter. Men kan zien dat σ, S , F , en x max grote invloed op de P max , zoals weergegeven in Fig. 3a-d. De P max neemt dramatisch toe als σ, S , F , en x max toenemen. De parameter σ en S bepalen voornamelijk het bedrag van de kosten die kunnen worden overgedragen. De parameters F en x max voornamelijk de bewegingsvergelijkingen beïnvloeden. De bijbehorende optimale weerstand neemt af met x max afnemend terwijl het zelden wordt beïnvloed door σ, S , en F. Bovendien zijn de parameters d en ε r hebben zelden invloed op de P max en bijbehorende weerstand, zoals aangegeven in Fig. 3e, f. Dat is de effectieve dikte van de diëlektrische laag d 0 = d /ε r die weinig invloed heeft op de prestaties van TENG's. We kunnen deze parameters aanpassen om het maximale vermogen te regelen. Het is vermeldenswaard dat de bijbehorende weerstand meestal de belastingsweerstand van elektronica is.
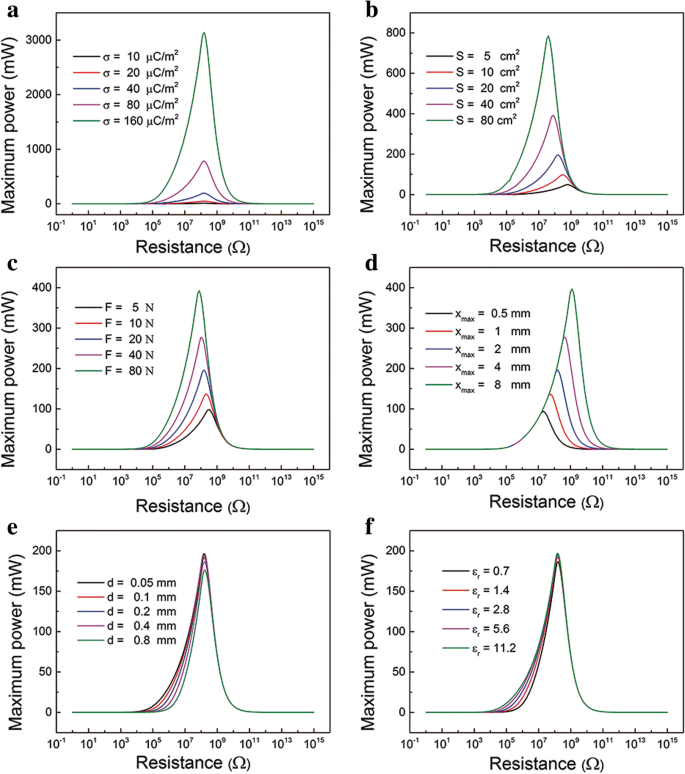
Het effect van parameters op P max en bijbehorende weerstand. Onmiddellijk energieprofiel met R op verschillende a oppervlakteladingsdichtheid σ, b oppervlakte grootte S , c drukkracht F , d maximale scheidingsafstand x max , e dikte van de diëlektrische laag d , en f ε r
Veersysteem
Voor een meer populaire experimentconditie is het veersysteem inbegrepen. De drukkracht F wordt periodiek toegepast, zoals weergegeven in figuur 4a. In het scheidingsproces (T = t 1 ), is er alleen herstelkracht van veren en zwaartekracht, dus F = 0. Tijdens het contactproces (T = t 2 + t 3 ), de drukkracht F is toegevoegd. En het zou nog lang duren nadat de twee lagen volledig in contact waren gekomen. De bewegingscurven worden getoond in Fig. 4b. De berekende bewegingsvergelijkingen en uitgangsprestaties worden als volgt afgeleid. (Aanvullend bestand 1:Note 3 in de ESM)
$$ \mathrm{x}(t)={x}_{\mathrm{max}}-{x}_{\mathrm{max}}\mathit{\cos}\left({\omega}_0t\right ) $$ (9.1) $$ \mathrm{x}(t)={x}_{\mathrm{max}}-\frac{F}{k}+\frac{F}{k}\cos \left ({\omega}_0t\right) $$ (9,2)waarbij \( {\omega}_0^2=k/m \). En de EQ's. (9.1) en (9.2) vertegenwoordigen respectievelijk het scheidingsproces en het contactproces.
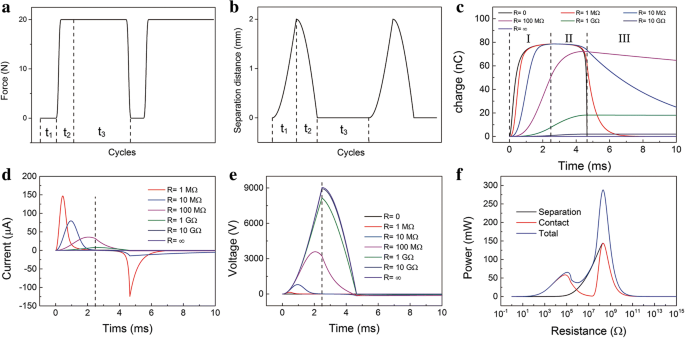
Berekende kenmerken van de contactscheidingsmodus TENGs. een De periodieke kracht F . b De periodieke beweging van de toplaag. c Overgedragen kosten-tijd relatie bij verschillende R in het contact- en scheidingsproces. d Huidige-tijd relatie op verschillende R in het contact- en scheidingsproces. e Spanning-tijdrelatie bij verschillende R in het contact- en scheidingsproces. v De relaties van onmiddellijk maximaal vermogen met weerstanden in het contact, de scheiding en het hele proces
In het scheidingsproces:
$$ {\displaystyle \begin{array}{c}Q(t)={\int}_0^t\frac{\sigma {x}_{\mathrm{max}}\left (1-\mathit{\ cos}\left({\omega}_0t\right)\right)}{R{\varepsilon}_0}\mathit{\exp}\left(\frac{d_0+{x}_{\mathrm{max}}} {RS{\varepsilon}_0}t-\frac{x_{\mathrm{max}}}{RS{\varepsilon}_0{\omega}_0}\mathit{\sin}\left({\omega}_0t\ right)\right) dt\\ {}\times \mathit{\exp}\left(-\frac{d_0+{x}_{\mathrm{max}}}{RS{\varepsilon}_0}t+\frac{ x_{\mathrm{max}}}{RS{\varepsilon}_0{\omega}_0}\mathit{\sin}\left({\omega}_0t\right)\right),t<{t}_1\ einde{array}} $$ (10)In het contactproces:
$$ {\displaystyle \begin{array}{l}Q(t)=\mathit{\exp}\left(-\frac{d_0+{x}_{\mathrm{max}}-\frac{F}{ k}}{RS{\varepsilon}_0}t+\frac{Fsin\left({\omega}_0t\right)}{kRS{\varepsilon}_0{\omega}_0}\right)\\ {}\times \left\{{q}_0+{\int}_0^t\mathit{\exp}\left(\frac{d_0+{x}_{\mathrm{max}}-\frac{F}{k}}{ RS{\varepsilon}_0}t-\frac{Fsin\left({\omega}_0t\right)}{kRS{\varepsilon}_0{\omega}_0}\right)\right.\ \\ {}\ \\ {}\times \left.\frac{\sigma \left({x}_{\mathrm{max}}-\frac{F}{k}+\frac{F}{k}\cos \left ({\omega}_0t\right)\right)}{R{\varepsilon}_0} dt\right\},t<{t}_2\ \end{array}} $$ (11) $$ Q(t )={Q}_0\times \mathit{\exp}\left(\frac{d_0}{RS{\varepsilon}_0}\left({t}_0-t\right)\right),t\ge { t}_3 $$ (12)waar q 0 zijn de kosten die tijdens het scheidingsproces zijn overgedragen van de BE naar de TE.
De uitgangsstroom en spanning kunnen worden berekend als I (t ) = dQ /dt en V (t ) = RI (t ).
De overgedragen kosten-tijd relatie op verschillende R in het volledige proces is uitgezet in figuur 4c. Het ladingsoverdrachtsproces is verdeeld in drie gebieden, wat overeenkomt met de periodieke kracht. Regio I vertegenwoordigt het scheidingsproces en het contactproces bevat de regio's II en III. In regio I worden de heffingen vanuit de BE overgedragen aan de TE. De lasten in de TE blijven stijgen. In gebied II is de richting van de ladingsstroom gerelateerd aan de weerstand. De ladingen in de TE blijven toenemen wanneer de weerstand groot is (R ≥ 1 GΩ). Het neemt toe tot het maximum en neemt vervolgens af wanneer de weerstand laag is (R ≤ 100 MΩ). Vooral wanneer R = 0, zullen de tarieven in regio II blijven dalen. In regio III blijven de lasten in de TE dalen. De overeenkomstige uitgangsstroom in het hele proces wordt getoond in figuur 4d. De stroom in het scheidings- en contactproces heeft het tegenovergestelde teken. Meestal is de maximale stroomwaarde in het scheidingsproces iets groter dan die in het contactproces. Interessant is dat in het contactproces de absolute maximale stroomwaarde verschijnt aan het begin van het contactproces of op het moment dat ze net contact hebben. Wanneer de weerstand groot is, verschijnt deze aan het begin van het contactproces, omgekeerd. De uitgangsspanning neemt met de tijd toe en neemt vervolgens af, zoals weergegeven in figuur 4e. De uitgangsspanning zou verschijnen als een negatieve waarde in het contactproces. En de absolute waarde is veel kleiner dan die in het scheidingsproces. Deze cijfers komen overeen met gemeten experimentele grafieken in de literatuur. De gemeten uitgangsstroom is duidelijk wisselend en de gemeten uitgangsspanning is meestal piekscherp. De relaties van onmiddellijk maximaal vermogen met weerstanden in het contact, de scheiding en het hele proces worden getoond in Fig. 4f. De TENG's bereikt zijn absolute maximale momentane vermogen rond 200 MΩ in het scheidings- en contactproces. Tijdens het contactproces heeft het een extra lokale maximale waarde van ongeveer 0,1 MΩ. Dus in het hele proces krijgt het momentane vermogen zijn maximale waarde rond de 200 MΩ. Men kan zien dat de vermogenscurve van het contactproces die van het scheidingsproces overlapt wanneer de weerstand groot is. Omdat de maximale stroomwaarde verschijnt op het snijpunt van beide processen wanneer R ≥ 200 MΩ.
Bovendien zijn de berekende resultaten van P max en de bijbehorende optimale weerstand zijn uitgezet in figuur 5. Zoals aangegeven in figuur 5a-c, neemt het maximale momentane vermogen toe naarmate de parameters x max , S , en k toenemen. Dit kan worden bijgedragen aan de hogere overdrachtssnelheid van de elektronen. Tegelijkertijd verandert ook de bijbehorende optimale weerstand. De optimale weerstand neemt af met S en k toenemend, maar de omgekeerde trend met x max . De invloed van parameters σ op de P max en optimale weerstand wordt getoond in Fig. 5d. De P max neemt snel toe met toenemende σ, terwijl de optimale weerstand constant blijft. De optimale weerstand wordt ook niet beïnvloed door ε r . Maar als ε r neemt toe, neemt het maximale momentane vermogen toe en raakt dan verzadigd. De F heeft vrijwel geen invloed op het maximale momentane vermogen en optimale weerstand. In het hele contact- en scheidingsproces is de F heeft alleen invloed op het contactproces. Dus de maximale stroom in het scheidingsproces blijft hetzelfde. Zoals geïllustreerd in figuur 5f, verandert het maximale momentane vermogen niet. Dit is anders dan het niet-veersysteem. In het niet-veersysteem is de F heeft direct invloed op het scheidingsproces en dus op het maximale vermogen.
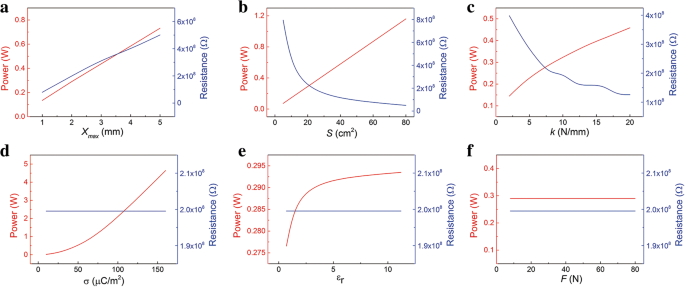
Invloed van de parameters op de P max en bijbehorende weerstand in één cyclus. De relatie van P max en bijbehorende weerstand met de parameters a x max , b S , c k , d , e ε r , en f F
Kortom, de P max kan worden vergroot door de maximale scheidingsafstand x . te vergroten max , gebied S , veercoëfficiënt k , relatieve permittiviteit van diëlektrische laag ε r , en vooral oppervlakteladingsdichtheid σ. Bijvoorbeeld materiaalparameters zoals ε r en σ zijn meestal geoptimaliseerd om een hoger vermogen te krijgen [28, 29]. Terwijl de optimale weerstand kan worden aangepast door de parameters x max , S , en k . De P max en optimale weerstand hangen voornamelijk af van de materiaal- en constructieparameters.
Conversie-efficiëntie η van TENG's
Soms maken we ons meer zorgen over P max dat we de η . negeren . Efficiëntie is een belangrijke parameter om een stroombron te evalueren. η wordt gedefinieerd als de verhouding tussen de output elektrische energie en de input mechanische energie. Hier hebben we systematisch en direct de invloed van deze parameters op de efficiëntie onderzocht.
De elektrische energie en mechanische energie worden verkregen volgens de huidige puls bij optimale R . De output elektrische energie wordt gegeven door
$$ {E}_{\mathrm{electric}}={\int}_{t_{\mathrm{start}}}^{t_{\mathrm{end}}}{I}^2 Rdt $$ (13 )waarbij de tijdspanne tussen t begin en t einde drukt een heel contact- en scheidingsproces uit.
De berekende mechanische energie is
$$ {E}_{\mathrm{mechanical}}=F\times S $$ (14)Dus de η wordt als volgt berekend
$$ \eta =\frac{E_{\mathrm{electric}}}{E_{\mathrm{mechanical}}}\times 100\% $$ (15)De relatie van η met x max werd getoond in Fig. 6a. Als x max neemt toe, de efficiëntie η neemt toe en raakt dan geleidelijk verzadigd. We weten dat de mechanische energie en het maximale vermogen evenredig is met x max . Echter, het verhogen van x max zal de scherpte van de huidige-tijdcurve veranderen. Het betekent dat de groeisnelheid zal vertragen wanneer x max groter is. De invloed van parameters S , k , en σ op η worden getoond in Fig. 6b-d. De stijgende trend van de efficiëntie η met deze parameters is vergelijkbaar met die van het maximale vermogen. De efficiëntie η neemt geleidelijk toe met de S en k toenemend. Opmerkelijk is dat de σ grote invloed kan hebben op de efficiëntie η . De parameter ε r is moeilijk te veranderen, en gelukkig heeft het bijna geen invloed op η zoals getoond in Fig. 6e. Zoals getoond in Fig. 6f, is de efficiëntie η neemt snel af als F neemt toe. Dit wordt voornamelijk bijgedragen aan de toename van mechanische energie. Uiteraard is het rendement relatief laag. Gelukkig kunnen we de efficiëntie enorm verhogen door σ te verbeteren.
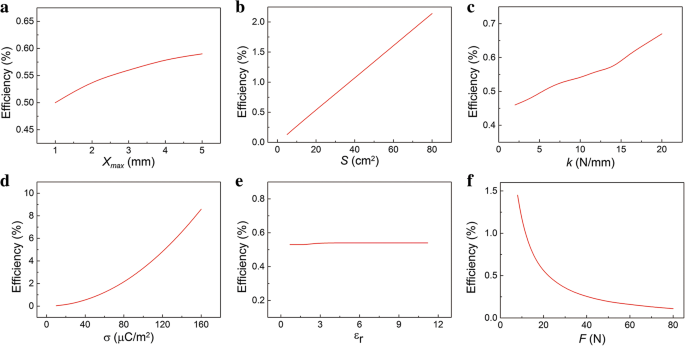
Conversie-efficiëntie η van TENG. De relatie van de berekende conversie-efficiëntie met de parameters a x max , b S , c k , d , e ε r , en f F
In de praktijk kan de F kan de parameter σ [30] beïnvloeden. Onder kleine F , de twee lagen zijn gedeeltelijk contact. De twee lagen kunnen beter contact krijgen als F neemt toe. Dan de parameter F kan bijna de oppervlakteladingsdichtheid σ beïnvloeden. Dat is de σ die toeneemt met de F raakt dan verzadigd, zoals weergegeven in figuur 7a. Daarom hebben we de relatie tussen de uitvoerprestaties en de drukkracht opnieuw berekend F . De invloed van F over maximale stroom, spanning en momentaan vermogen worden respectievelijk getoond in Fig. 7b-d. Ze hebben een vergelijkbare relatie met F . De uitgangsspanning neemt bijvoorbeeld toe met F toenemen en vervolgens constant houden, wat consistent is met de experimentgegevens in de literatuur [31, 32]. De invloed van F op elektrische energie wordt getoond in Fig. 7e. Opgemerkt moet worden dat er een keerpunt in de curve is. De output elektrische energie neemt toe met F toenemen en dan iets afnemen. De lichte daling van de output elektrische energie is te wijten aan het kortere contactproces onder grotere F . Onder kleine drukkracht, de F is evenredig met de σ, wat resulteert in een grotere output elektrische energie. Onder een grote drukkracht raakt de echter verzadigd. De overgedragen ladingen in het scheidingsproces blijven constant terwijl ze afnemen in het contactproces onder grotere drukkracht. Dus de output elektrische energie in het hele scheidings- en contactproces daalt lichtjes. De relatie van η en F wordt weergegeven in Fig. 7f. Interessant is dat de η -F curve is een piekscherp en de maximale waarde verscheen bij F ≈ 50 N. De invoer E mechanisch is evenredig met F , terwijl E mechanisch is veel groter dan output E elektrisch . Onder kleine F , de groeisnelheid van E elektrisch is sneller dan E mechanisch door de snelle stijging van σ. Echter, onder grote F , de afname van E elektrisch en verhoging van E mechanisch resulteren in een lager rendement. Het keerpunt in de relatie tussen energieconversie-efficiëntie en drukkracht is belangrijk bij het ontwerp van een effectieve krachtbron.
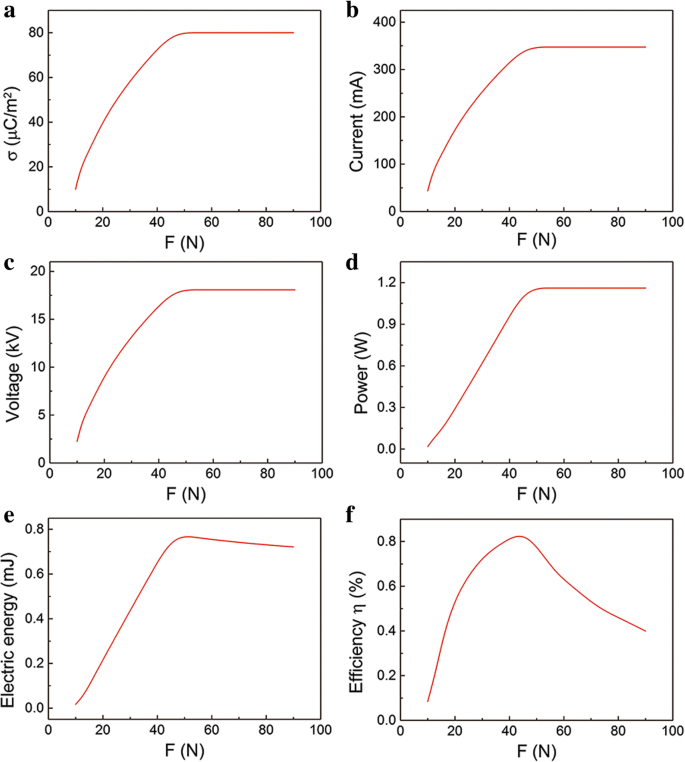
De relatie tussen uitvoerprestaties en de drukkracht F in praktijksituatie. een De invloed van drukkracht F op een oppervlakteladingsdichtheid σ, b maximale stroom, c maximale spanning, d maximaal momentaan vermogen, e elektrische energie, en f efficiëntie
Om hogere outputprestaties te krijgen, zoals stroom en onmiddellijk vermogen, een grote drukkracht F meestal wordt toegepast. Maar dat kan een laag conversierendement veroorzaken. Volgens de bovenstaande analyse kunnen we een rationele F . kiezen om zowel het hoge vermogen als de conversie-efficiëntie te krijgen.
Conclusie
Tot slot hebben we een praktische benadering geïntroduceerd om de conversie-efficiëntie van TENG's met contactmodus systemisch en direct te analyseren. Verder dan de conventionele analyse, werd een compressiekracht geïntroduceerd om een veelzijdiger bewegingsprofiel af te leiden, wat een beter begrip opleverde van het werkingsprincipe van het contactscheidingsproces. De expliciete vergelijkingen voor de belangrijke apparaatprestaties in het hele scheidings- en contactproces werden gepresenteerd, in tegenstelling tot de conventionele analyse die zich alleen op het scheidingsproces concentreert. Ten eerste hebben we de relatie tussen outputprestaties en materiaal-, structuur- en experimentele parameters geanalyseerd, voornamelijk voor een hoger uitgangsvermogen. Belangrijker nog, we hebben systematisch en diepgaand de invloed van deze parameters op de energieconversie-efficiëntie in het hele proces bestudeerd. Belangrijk is dat er een keerpunt werd gevonden in de relatie tussen conversie-efficiëntie en drukkracht. De TENG's met een hoog uitgangsvermogen en een hoge conversie-efficiëntie kunnen tegelijkertijd onder optimale kracht worden verkregen. Het is realistisch en nuttig voor efficiëntere TENG's. Belangrijk is dat het een goede kans maakt om de normen vast te stellen voor het kwantificeren van de efficiëntie van TENG's, wat de basis legt voor de verdere industrialisatie en multifunctionaliteit van TENG's.
Afkortingen
- BE:
-
Onderste elektrode
- TE:
-
Bovenste elektrode
- TENG's:
-
Tribo-elektrische nanogeneratoren
Nanomaterialen
- Zonne-verwarmingssysteem
- Hoe de machine-efficiëntie berekenen?
- Hoogrendement grafeen zonnecellen
- BD lanceert oplossing voor moleculaire diagnostische testen met hoge doorvoer
- Mogelijkheden voor energie-efficiëntie in pompsystemen
- 5G Telco's richten zich op energie-efficiëntie
- Samenwerken om efficiëntie te verbeteren
- Uw systeem beoordelen op manieren om het energieverbruik te verminderen
- Optimalisatie van leidingconfiguraties voor energie-efficiëntie
- Optimalisatie van energie-efficiëntie met centrale controllers en bewaking op afstand
- 5 tips voor energiezuinige perslucht



