Waarheidstabellen converteren naar Booleaanse uitdrukkingen

Bij het ontwerpen van digitale schakelingen begint de ontwerper vaak met een waarheidstabel die beschrijft wat de schakeling zou moeten doen.

De ontwerptaak ​​is grotendeels om te bepalen welk type circuit de functie zal vervullen die wordt beschreven in de waarheidstabel.

Hoewel sommige mensen een natuurlijk vermogen lijken te hebben om naar een waarheidstabel te kijken en zich onmiddellijk de noodzakelijke logische poort- of relaisschakelingen voor de taak voor te stellen, zijn er procedurele technieken beschikbaar voor de rest van ons.

Hier bewijst Booleaanse algebra zijn nut op een zeer dramatische manier.

Om deze procedurele methode te illustreren, moeten we beginnen met een realistisch ontwerpprobleem.

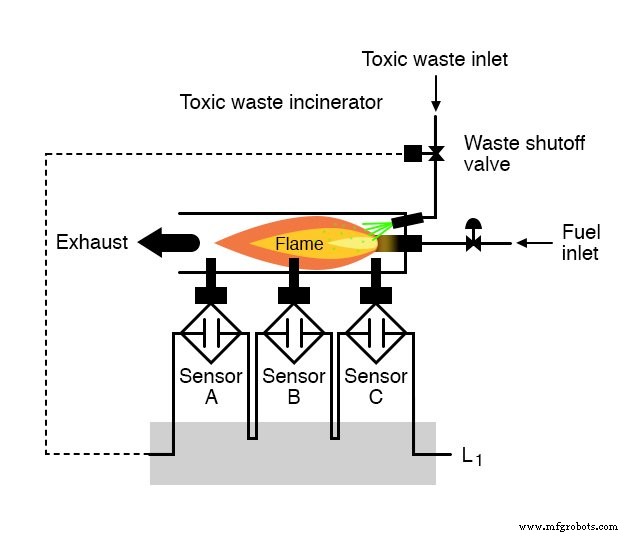
Stel dat we de opdracht kregen om een ​​vlamdetectiecircuit te ontwerpen voor een gifverbrandingsoven.

De intense hitte van het vuur is bedoeld om de giftigheid van het afval dat in de verbrandingsoven wordt gebracht te neutraliseren.

Dergelijke op verbranding gebaseerde technieken worden vaak gebruikt om medisch afval te neutraliseren, dat besmet kan zijn met dodelijke virussen of bacteriën:

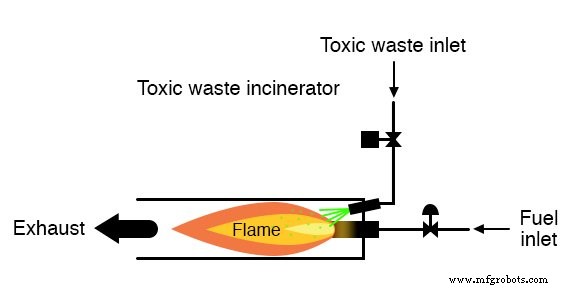
Zolang er een vlam in de verbrandingsoven wordt gehouden, is het veilig om er afval in te spuiten om het te neutraliseren.

Als de vlam zou worden gedoofd, zou het echter onveilig zijn om afval in de verbrandingskamer te blijven injecteren, omdat het de uitlaat niet-geneutraliseerd zou verlaten en een gevaar voor de gezondheid zou vormen voor iedereen in de buurt van de uitlaat.

Wat we nodig hebben in dit systeem is een zekere manier om de aanwezigheid van een vlam te detecteren, en om het injecteren van afval alleen toe te staan ​​als een vlam is "bewezen" door het vlamdetectiesysteem.

Er bestaan ​​verschillende vlamdetectietechnologieën:optische (detectie van licht), thermische (detectie van hoge temperatuur) en elektrische geleiding (detectie van geïoniseerde deeltjes in het vlampad), elk met zijn unieke voor- en nadelen.

Stel dat vanwege het hoge risico dat gepaard gaat met het eventueel afvoeren van niet-geneutraliseerd afval uit de uitlaat van deze verbrandingsoven, wordt besloten het vlamdetectiesysteem overbodig te maken (meerdere sensoren), zodat uitval van een enkele sensor niet leidt tot tot een uitstoot van gifstoffen uit de uitlaat.

Elke sensor is uitgerust met een normaal open contact (open indien geen vlam, gesloten indien vlam gedetecteerd) dat we zullen gebruiken om de ingangen van een logisch systeem te activeren:

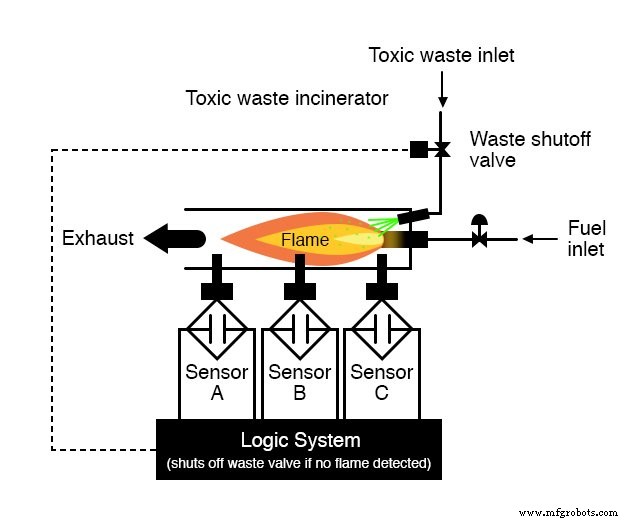
Het is nu onze taak om de schakelingen van het logische systeem te ontwerpen om de afvalklep te openen als en alleen als er een goede vlam is, bewezen door de sensoren.

Maar eerst moeten we beslissen wat het logische gedrag van dit controlesysteem moet zijn.

Willen we dat de klep wordt geopend als slechts één van de drie sensoren een vlam detecteert? Waarschijnlijk niet, omdat dit het doel van het hebben van meerdere sensoren teniet zou doen.

Als een van de sensoren op een zodanige manier zou falen dat de aanwezigheid van een vlam ten onrechte wordt aangegeven terwijl die er niet was, zou een logisch systeem gebaseerd op het principe van "elke van de drie sensoren die vlam tonen" dezelfde output geven die een systeem met één sensor zou hetzelfde falen.

Een veel betere oplossing zou zijn om het systeem zo te ontwerpen dat de klep het commando krijgt om te openen als en alleen als alle drie de sensoren detecteer een goede vlam.

Op deze manier kon een enkele, defecte sensor die valselijk vlam vertoonde de klep niet in de open positie houden; in plaats daarvan zouden alle drie de sensoren op dezelfde manier moeten falen - een hoogst onwaarschijnlijk scenario - om deze gevaarlijke situatie te laten optreden.

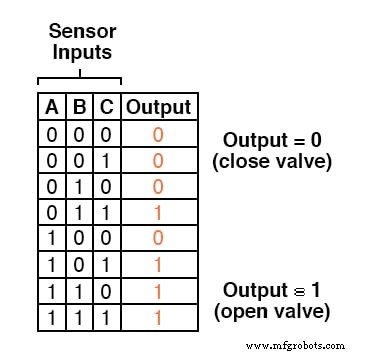
Onze waarheidstabel zou er dus als volgt uitzien:

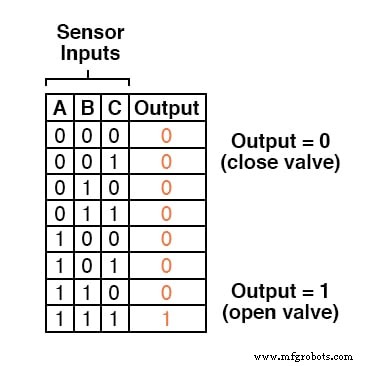
Er is niet veel inzicht voor nodig om te beseffen dat deze functionaliteit kan worden gegenereerd met een AND-poort met drie ingangen:de uitgang van de schakeling zal "hoog" zijn als en slechts als ingang A AND voer B EN in ingang C zijn allemaal "hoog:"

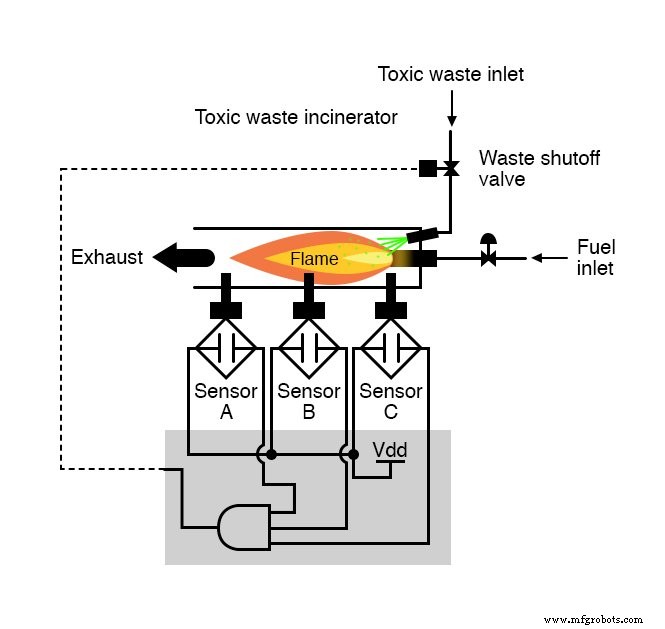
Als we relaisschakelingen gebruiken, kunnen we deze EN-functie creëren door drie relaiscontacten in serie te schakelen, of gewoon door de drie sensorcontacten in serie te schakelen, zodat de enige manier waarop elektrische stroom kan worden gestuurd om de afvalklep te openen, is als alle drie de sensoren vlam aangeven:

Hoewel deze ontwerpstrategie de veiligheid maximaliseert, maakt het het systeem erg vatbaar voor sensorstoringen van het tegenovergestelde soort.

Stel dat een van de drie sensoren zodanig zou falen dat deze geen vlam aangaf terwijl er echt een goede vlam was in de verbrandingskamer van de verbrandingsoven.

Die enkele storing zou de afvalklep onnodig afsluiten, wat resulteert in verloren productietijd en verspilling van brandstof (het voeden van een vuur dat niet werd gebruikt om afval te verbranden).

Het zou leuk zijn om een ​​logisch systeem te hebben dat dit soort storingen mogelijk maakt zonder het systeem onnodig uit te schakelen, maar toch sensorredundantie biedt om de veiligheid te behouden in het geval dat een enkele sensor "hoog" faalt (te allen tijde vlam tonend , of er al dan niet een te detecteren was).

Een strategie die aan beide behoeften zou voldoen, zou een "twee van de drie" sensorlogica zijn, waarbij de afvalklep wordt geopend als ten minste twee van de drie sensoren een goede vlam vertonen.

De waarheidstabel voor zo'n systeem ziet er als volgt uit:

Sum-Of-Products gebruiken

Hier is het niet per se duidelijk wat voor soort logisch circuit zou voldoen aan de waarheidstabel.

Een eenvoudige methode voor het ontwerpen van zo'n circuit is echter te vinden in een standaardvorm van Booleaanse uitdrukking genaamd de Sum-Of-Products , of SOP , formulier.

Zoals je zou kunnen vermoeden, is een Sum-Of-Products Booleaanse uitdrukking letterlijk een set Booleaanse termen die zijn toegevoegd (opgeteld ) samen, waarbij elke term een ​​multiplicatief is (product ) combinatie van Booleaanse variabelen.

Een voorbeeld van een SOP-expressie zou er ongeveer zo uit kunnen zien:ABC + BC + DF, de som van de producten "ABC", "BC" en "DF".

Sum-Of-Products-uitdrukkingen zijn eenvoudig te genereren uit waarheidstabellen.

Het enige wat we hoeven te doen is de waarheidstabel onderzoeken voor alle rijen waar de uitvoer "hoog" is (1), en een Booleaanse productterm schrijven die gelijk zou zijn aan een waarde van 1 gegeven die invoervoorwaarden.

Bijvoorbeeld, in de vierde rij beneden in de waarheidstabel voor ons twee-uit-drie logische systeem, waar A=0, B=1 en C=1, zou de productterm A'BC zijn, aangezien die term zou een waarde van 1 hebben als en slechts als A=0, B=1 en C=1:

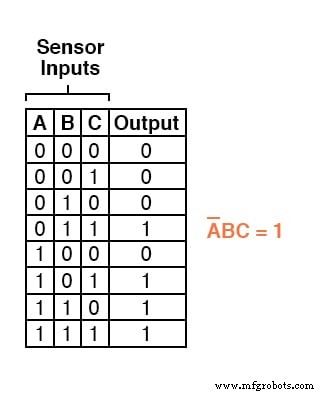
Drie andere rijen van de waarheidstabel hebben een uitvoerwaarde van 1, dus die rijen hebben ook Booleaanse productexpressies nodig om ze weer te geven:

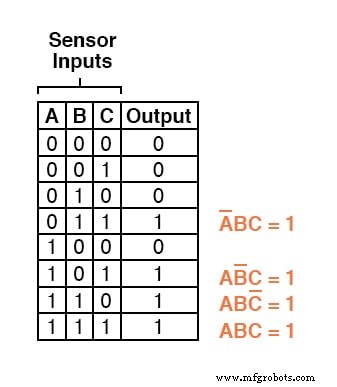
Ten slotte voegen we deze vier Booleaanse productuitdrukkingen samen door ze op te tellen, om een ​​enkele Booleaanse uitdrukking te creëren die de waarheidstabel als geheel beschrijft:

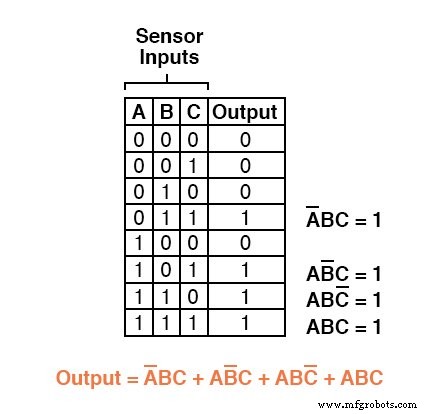
Nu we een Booleaanse Sum-Of-Products-expressie hebben voor de functie van de waarheidstabel, kunnen we eenvoudig een logische poort of logische relaisschakeling ontwerpen op basis van die expressie:

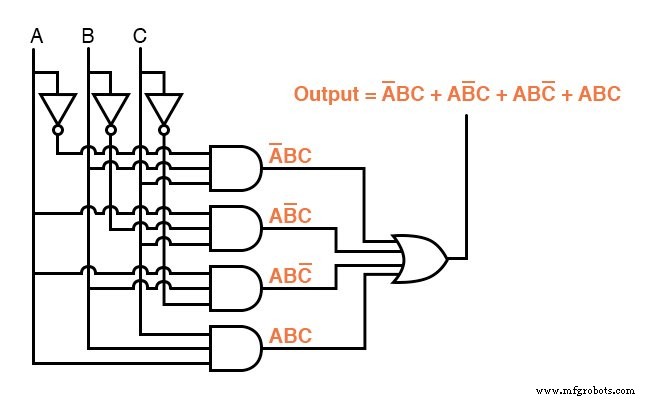
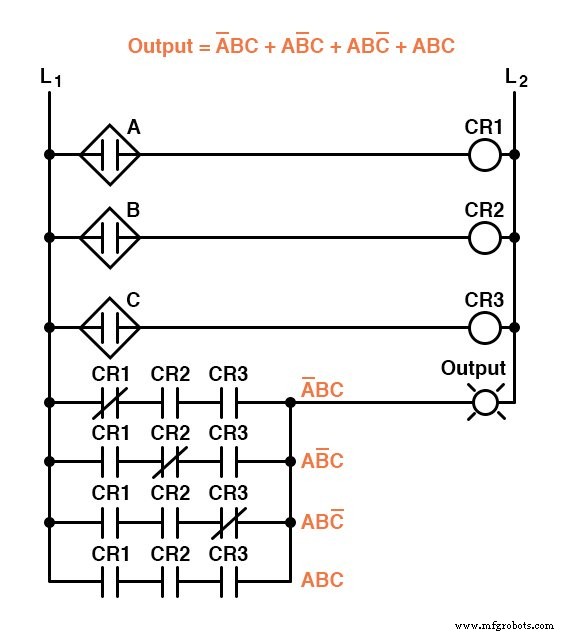
Helaas zijn beide circuits behoorlijk complex en zouden ze kunnen worden vereenvoudigd.

Met behulp van Booleaanse algebra-technieken kan de uitdrukking aanzienlijk worden vereenvoudigd:

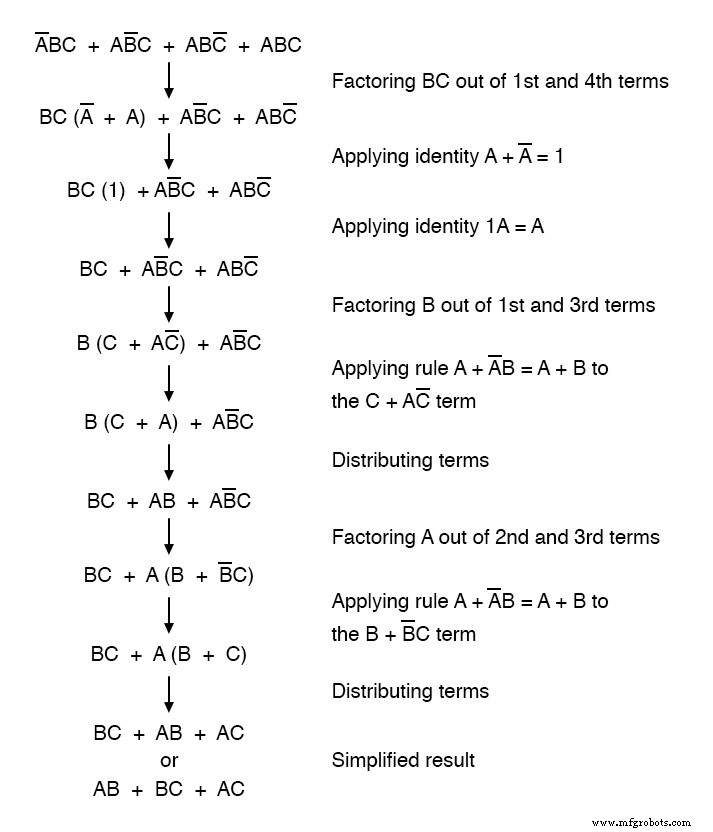
Als resultaat van de vereenvoudiging kunnen we nu veel eenvoudiger logische circuits bouwen die dezelfde functie vervullen, in poort- of relaisvorm:

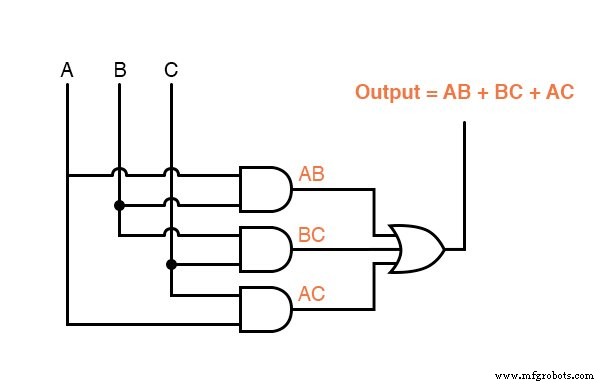
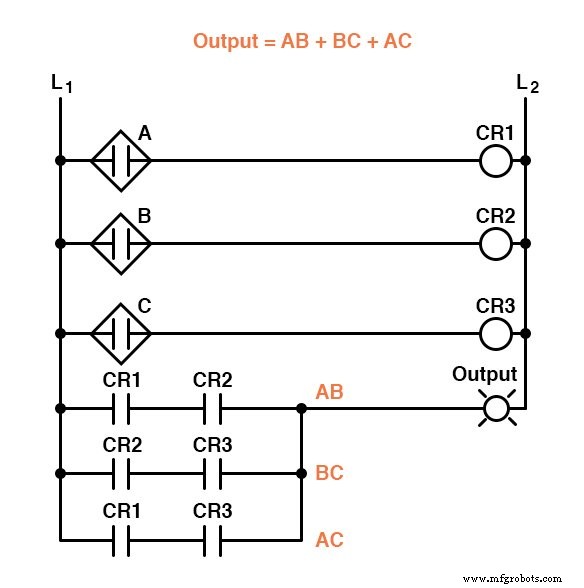
Elk van deze circuits zal de taak van het bedienen van de afvalklep van de verbrandingsoven adequaat uitvoeren op basis van een vlamverificatie van twee van de drie vlamsensoren.

Dit is tenminste wat we nodig hebben voor een veilig verbrandingssysteem.

We kunnen de functionaliteit van het systeem echter uitbreiden door er logische schakelingen aan toe te voegen die zijn ontworpen om te detecteren of een van de sensoren het niet eens is met de andere twee.

Als alle drie de sensoren goed werken, moeten ze de vlam met dezelfde nauwkeurigheid detecteren.

Ze moeten dus ofwel allemaal 'laag' (000:geen vlam) of allemaal 'hoog' (111:goede vlam) registreren.

Elke andere uitgangscombinatie (001, 010, 011, 100, 101 of 110) vormt een meningsverschil tussen sensoren en kan daarom dienen als een indicator voor een mogelijke sensorstoring.

Als we circuits zouden toevoegen om een ​​van de zes "sensor-onenigheid"-condities te detecteren, zouden we de output van dat circuit kunnen gebruiken om een ​​alarm te activeren.

Degene die de verbrandingsoven in de gaten houdt, zal dan zijn oordeel vellen door ofwel door te gaan met werken met een mogelijk defecte sensor (ingangen:011, 101 of 110), of de verbrandingsoven volledig veilig uit te schakelen.

Als de verbrandingsoven is uitgeschakeld (geen vlam) en een of meer van de sensoren nog steeds een vlam aangeven (001, 010, 011, 100, 101 of 110), terwijl de andere sensoren geen vlam aangeven, het zal bekend zijn dat er een duidelijk sensorprobleem bestaat.

De eerste stap bij het ontwerpen van dit detectiecircuit voor "sensor-onenigheid" is het schrijven van een waarheidstabel waarin het gedrag wordt beschreven.

Aangezien we al een waarheidstabel hebben die de uitvoer van het logische circuit "goede vlam" beschrijft, kunnen we eenvoudig een andere uitvoerkolom aan de tabel toevoegen om het tweede circuit weer te geven, en een tabel maken die het hele logische systeem vertegenwoordigt:

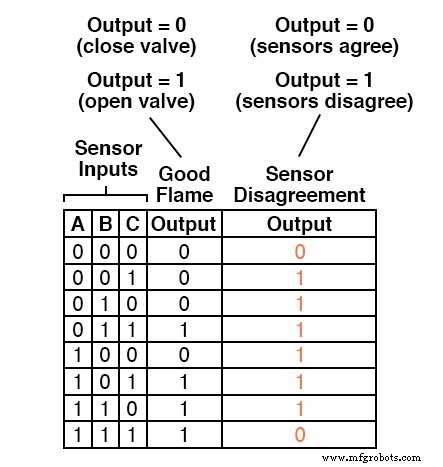
Hoewel het mogelijk is om een ​​Sum-Of-Products-expressie te genereren voor deze nieuwe waarheidstabelkolom, zijn er zes termen van elk drie variabelen nodig!

Zo'n Booleaanse uitdrukking zou veel stappen vergen om te vereenvoudigen, met een groot potentieel voor het maken van algebraïsche fouten:

Product-van-sommen gebruiken

Een alternatief voor het genereren van een Sum-Of-Products-expressie om rekening te houden met alle "hoge" (1) uitvoervoorwaarden in de waarheidstabel, is het genereren van een Product-Of-Sums , of POS , expressie, om in plaats daarvan rekening te houden met alle "lage" (0) uitvoervoorwaarden.

Omdat er veel minder gevallen zijn van een "lage" uitvoer in de laatste waarheidstabelkolom, zou de resulterende Product-Of-Sums-expressie minder termen moeten bevatten.

Zoals de naam al doet vermoeden, is een Product-Of-Sums-expressie een reeks toegevoegde termen (sommen ), die worden vermenigvuldigd (product ) samen.

Een voorbeeld van een POS-uitdrukking is (A + B)(C + D), het product van de sommen "A + B" en "C + D".

Om te beginnen identificeren we welke rijen in de laatste waarheidstabelkolom "lage" (0) uitvoer hebben, en schrijven een Booleaanse somterm die gelijk zou zijn aan 0 voor de invoervoorwaarden van die rij.

Bijvoorbeeld, in de eerste rij van de waarheidstabel, waar A=0, B=0 en C=0, zou de somterm zijn (A + B + C), aangezien die term een ​​waarde van 0 zou hebben als en alleen als A=0, B=0 en C=0:

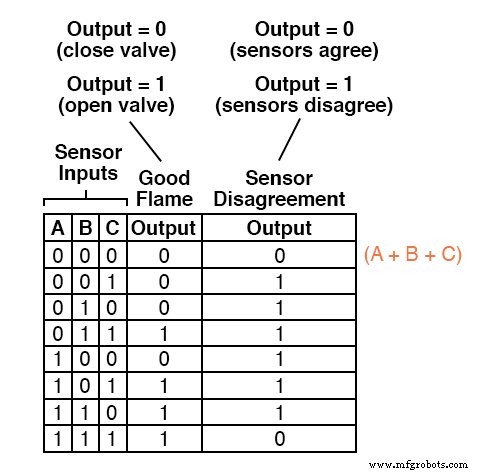
Slechts één andere rij in de laatste waarheidstabelkolom heeft een "lage" (0) output, dus alles wat we nodig hebben is nog een somterm om onze Product-Of-Sums-expressie te voltooien.

Deze laatste somterm vertegenwoordigt een 0-uitgang voor een ingangsconditie van A=1, B=1 en C=1.

Daarom moet de term worden geschreven als (A' + B'+ C'), omdat alleen de som van de aangevulde invoervariabelen zijn alleen voor die voorwaarde gelijk aan 0:

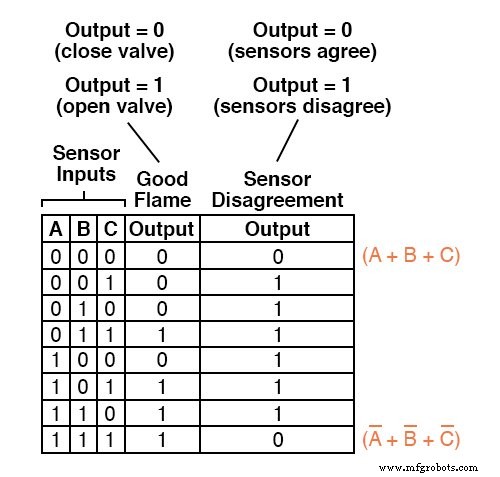
De voltooide Product-Of-Sums-uitdrukking is natuurlijk de multiplicatieve combinatie van deze twee somtermen:

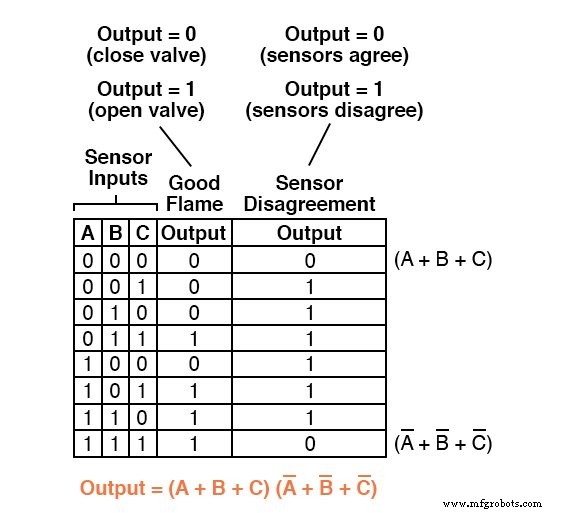
Terwijl een Sum-Of-Products-expressie zou kunnen worden geïmplementeerd in de vorm van een set AND-poorten waarvan de uitgangen verbonden zijn met een enkele OR-poort, kan een Product-Of-Sums-expressie worden geïmplementeerd als een set OR-poorten die in een enkele EN poort:

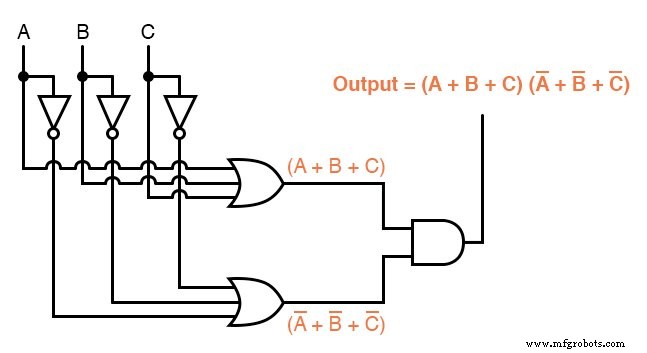
Dienovereenkomstig, terwijl een Sum-Of-Products-uitdrukking kan worden geïmplementeerd als een parallelle verzameling van in serie geschakelde relaiscontacten, kan een Product-Of-Sums-uitdrukking worden geïmplementeerd als een serieverzameling van parallel geschakelde relaiscontacten:

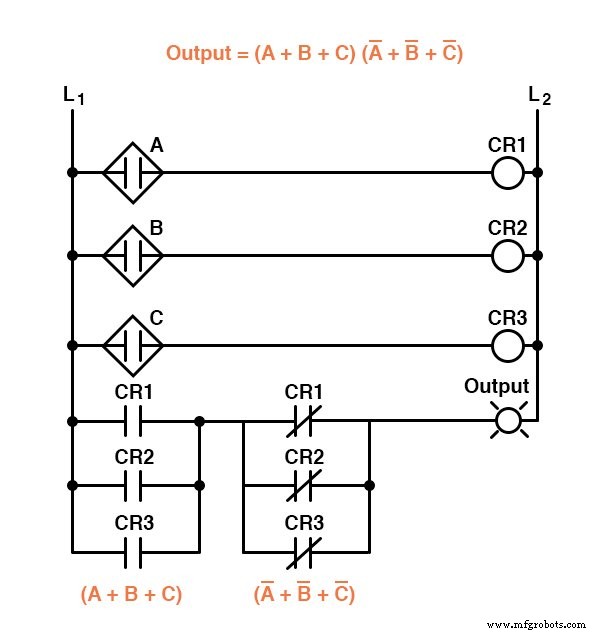
De vorige twee circuits vertegenwoordigen alleen verschillende versies van het "sensor-onenigheid"-logische circuit, niet de "goede vlam"-detectiecircuit(s).

Het hele logische systeem zou de combinatie zijn van zowel "goede vlam"- als "sensoronenigheid"-circuits, weergegeven in hetzelfde diagram.

Geïmplementeerd in een Programmable Logic Controller (PLC), kan het hele logische systeem er ongeveer zo uitzien:

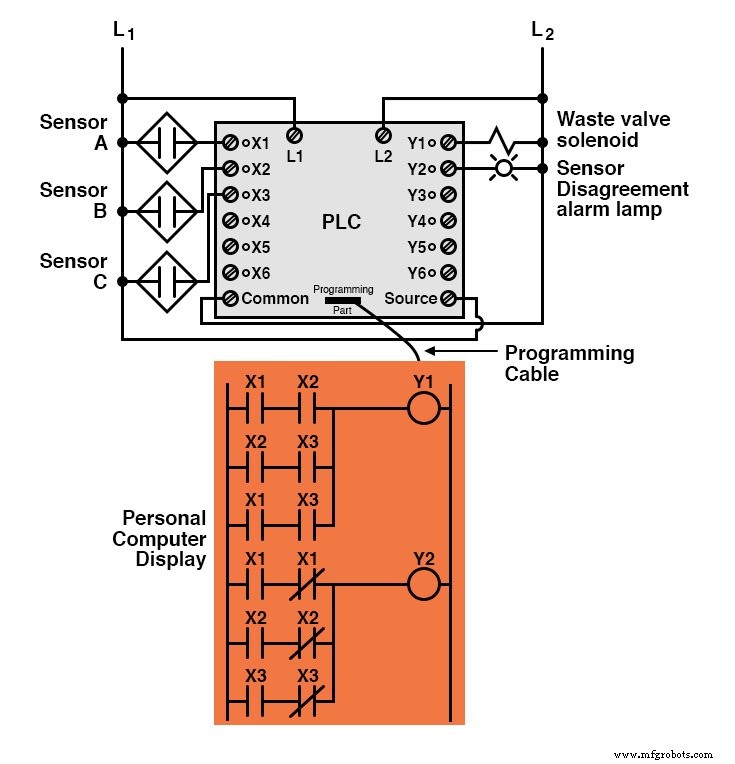
Zoals u kunt zien, zijn zowel de standaard Booleaanse formulieren Sum-Of-Products als Products-Of-Sums krachtige hulpmiddelen wanneer ze worden toegepast op waarheidstabellen.

Ze stellen ons in staat om een ​​Booleaanse uitdrukking - en uiteindelijk een echt logisch circuit - af te leiden uit niets anders dan een waarheidstabel, wat een geschreven specificatie is voor wat we willen dat een logisch circuit doet.

Om met behulp van eenvoudige, deterministische procedures van een geschreven specificatie naar een daadwerkelijke schakeling te kunnen gaan, betekent dat het mogelijk is om het ontwerpproces voor een digitale schakeling te automatiseren.

Met andere woorden, een computer kan worden geprogrammeerd om een ​​aangepast logisch circuit te ontwerpen op basis van een waarheidstabelspecificatie!

De stappen die moeten worden genomen van een waarheidstabel naar het uiteindelijke circuit zijn zo ondubbelzinnig en direct dat het weinig of geen creativiteit of andere originele gedachte vereist om ze uit te voeren.

BEOORDELING:

• Som-van-producten , of SOP , Booleaanse uitdrukkingen kunnen vrij eenvoudig worden gegenereerd uit waarheidstabellen, door te bepalen welke rijen van de tabel een uitvoer hebben van 1, één productterm voor elke rij te schrijven en tenslotte alle producttermen op te tellen. Dit creëert een Booleaanse uitdrukking die de waarheidstabel als geheel vertegenwoordigt.
• Sum-Of-Products-expressies lenen zich goed voor implementatie als een set EN-poorten (producten) die worden ingevoerd in een enkele OF-poort (som).
• Product-van-sommen , of POS , Booleaanse uitdrukkingen kunnen ook vrij eenvoudig worden gegenereerd uit waarheidstabellen, door te bepalen welke rijen van de tabel een uitvoer van 0 hebben, één somterm voor elke rij te schrijven en tenslotte alle somtermen te vermenigvuldigen. Dit creëert een Booleaanse uitdrukking die de waarheidstabel als geheel vertegenwoordigt.
• Product-of-Sums-expressies lenen zich goed voor implementatie als een set OF-poorten (sommen) die worden ingevoerd in een enkele EN-poort (product).

GERELATEERDE WERKBLAD:

• Werkblad Product-van-Sommen-uitdrukkingen
• Booleaanse algebra-werkblad