Verbeterde opsluiting van Terahertz-oppervlakteplasmonpolaritons in bulk Dirac halfmetaal-isolator-metalen golfgeleiders

Abstract

Een subgolflengte terahertz plasmonische golfgeleider op basis van bulk Dirac semi-metaal (BDS)-isolator-metaal (BIM) structuur wordt onderzocht, wat aangeeft dat er een geoptimaliseerd frequentiebereik is met een betere opsluiting en minder verlies. Een beperking in breedbandmodus tot λ ₀ /15 met een relatief laag verlies van 1,0 dB/λ ₀ kan worden behaald. We laten ook zien dat twee siliciumlinten die in de BIM-golfgeleider zijn geïntroduceerd, een dynamisch afstembaar filter kunnen vormen dat terahertz-oppervlakteplasmonpolaritonen op diepe subgolflengteschaal afstemt, die verder kan worden benut voor het ontwerp van ultracompacte THz-plasmonische apparaten met dynamische afstembaarheid. Onze resultaten kunnen ook potentiële toepassingen bieden bij optische filtering.

Achtergrond

De Terahertz (THz)-golf is de afgelopen decennia extreem populair geweest vanwege zijn innovatieve toepassingen, zoals THz-beeldvorming, biochemische detectie en communicatie [1,2,3]. Om de detectiegevoeligheid, beeldresolutie en integratieniveau van THz-apparaten te verbeteren, is het dringend gewenst om de THz-golf in een diepe subgolflengteschaal te beperken [4,5,6]. Surface plasmon polaritons (SPP's), de oppervlakte-elektromagnetische modi gestimuleerd door de interactie tussen elektron in de geleidingsband van edelmetaal en fotonen in zichtbare golflengten, planten zich voort langs de metaal-isolatorinterface en maken de manipulatie van licht mogelijk buiten de klassieke diffractielimiet [7]. Sommerfeld-Zenneck-modi, analoog van SPP's in zichtbare band, kunnen worden ondersteund door metaal in het THz-gebied. Metamaterialen en andere kunstmatige structuren, zoals periodieke pleisters, geperforeerde platen en koperen buizen, zijn voorgesteld om deze losjes gebonden oppervlaktegolven op maat te maken [8,9,10]. Helaas hebben slechte opsluiting, hoog intrinsiek verlies en passieve afstembaarheid van deze modus de praktische toepassingen ervan ernstig belemmerd.

Grafeenplasmonen, met relatief weinig verlies, dynamische afstembaarheid en extreme opsluiting tot THz-golven, bieden veelbelovende toepassingen in ultracompacte en dynamisch afstembare apparaten met een hoge resolutie. Duan et al. stellen een breedband-gate-afstembare grafeen-heterostructuur voor om coherent terahertz-plasmonen te genereren en te controleren met dynamische afstembaarheid en hogere efficiëntie. Een robuust verschilfrequentiesignaal kan worden gegenereerd vanwege de strakke opsluiting van het grafeenplasmonveld [11]. Duan et al. onderzoek eerst het discrete Talbot-effect in diëlektrische grafeen-plasmongolfgeleiderarrays bij THz-golflengten, wat een nieuw platform biedt voor zelfbeeld met hoge resolutie van THz-golven op nanoschaal [12]. Lin et al. stellen een ultracompacte, door plasmon geïnduceerde transparantiegolfgeleider voor, die potentiële toepassingen belooft in langzaam licht van THz-golven [13, 14]. Li et al. stellen een reeks functionele optische filters en absorbers voor op basis van 2D-materiaalplasmonen, die een hoge integratie [15], weinig verlies en dynamische afstembaarheid demonstreren [16,17,18]. Uit deze werken kunnen we overtuigen dat het de extreme opsluiting van oppervlakteplasmonen is die het mogelijk maakt om THz-golven op diepe subgolflengteschaal te manipuleren.

Onlangs is bulk Dirac-semimetalen (BDS), "3-D grafeen", in beeld gebracht vanwege de ultrahoge mobiliteit van de drager tot 9 × 10⁶ cm² V⁻¹ s⁻¹ , wat veel hoger is dan het beste grafeen van 2 × 10⁵ cm² V⁻¹ s⁻¹ [19]. In het algemeen geldt dat hoe hoger de mobiliteit van de drager is, hoe lager het intrinsieke verlies van plasmonen zou zijn. Bovendien kunnen de diëlektrische functies van BDS actief worden afgestemd door de Fermi-energie te veranderen. Het goede nieuws is dat BDS, zoals Na₃ Bi [19], Cd₃ Als₂ [20] en AlCuFe-quasikristallen [21] zijn gemakkelijker te verwerken en stabieler in vergelijking met grafeen, dat naar verwachting een nieuwe generatie plasmonisch materiaal zal zijn na grafeen. De modusbeperking van SPP's in de BDS-isolatorinterface is echter niet optimistisch. Ons recente werk heeft de manipulatie van de THz SPP's in dubbellaagse BDS-bladgolfgeleider onderzocht, wat aangeeft dat de symmetrische koppelingsmodus een betere opsluiting heeft dan de plasmonische golfgeleidermodus in monolaag BDS-film [22]. De modusindex van de symmetrische modus is 1,21 bij 1,0 THz met de Fermi-energie van BDS E _F = 70 meV, wat nog steeds onvoldoende is om te voldoen aan de vraag naar het manipuleren van THz-golven op een schaal met diepe subgolflengten.

In dit artikel stellen we een diepe subgolflengte BDS-isolator-metaal (BIM) golfgeleider voor met verbeterde opsluiting, relatief weinig verlies en gewenste afstembaarheid. Verspreidingsrelatie, voortplantingsverlies en filtertoepassing van deze zeer beperkte modus worden onderzocht. Interessant is dat er een geoptimaliseerd frequentiebereik is met een verbeterde opsluiting en een verminderd verlies, wat zelden is gemeld in de traditionele SPP-modus in metalen structuur. Een beperking in breedbandmodus tot λ ₀ /15 met een relatief laag verlies van 1,0 dB/λ ₀ kan worden behaald. Anders dan de eerder bestudeerde op BDS gebaseerde structuur, kan de modus van deze BIM-golfgeleider efficiënt worden verzonden via een ultrasmalle spleet met een breedte kleiner dan λ ₀ /2000. Door twee siliciumlinten als reflectiespiegels te nemen, is een dynamisch afstembare optische resonator bereikt. De resonantiefrequentie van de resonator kan dynamisch worden afgestemd door de Fermi-energie van BDS te variëren, wat toepassingen kan vinden in THz-omschakeling en -filtering.

Theorie en simulatie

De voorgestelde BIM plasmonische golfgeleider wordt schematisch weergegeven in figuur 1(a), waar de monolaag BDS-film met een dikte van 0,2 μm wordt geplaatst op een spleetbreedte g weg van het zilveren substraat gescheiden door de diëlektrische afstandhouder met permittiviteit ε _r . Het zilveren substraat in het THz-gebied kan worden behandeld als een perfecte elektrische geleider (PEC) grens. Voor het TM-gepolariseerde invallende licht kan de plasmonische golfgeleidermodus die is opgesloten in de metaal-isolatorinterface zich voortplanten langs de x richting met een golfvector k _SPP en exponentieel verval langs de y richting in de vrije ruimte. Door de juiste randvoorwaarden te combineren, wordt de golfvector k _SPP van de BIM-golfgeleider kan worden verkregen uit de volgende spreidingsrelatie:[23].

$$ -\frac{\varepsilon_r\sqrt{k_{\mathrm{SPP}}^2-{k}_0^2}}{\varepsilon_0\sqrt{k_{\mathrm{SPP}}^2-\frac{ \varepsilon_r{k}_0^2}{\varepsilon_0}}}=\left(1+\frac{i\sigma \sqrt{k_{\mathrm{SPP}}}^2-{k}_0^2}}{ {\omega \varepsilon}_0}\right)\tanh \left(g\sqrt{k_{\mathrm{SPP}}}^2-\frac{\varepsilon_r{k}_0^2}{\varepsilon_0}}\right ), $$ (1)

waar k ₀ is de golfvector van het invallende licht. Door het oplossen van Vgl. (1), we kunnen de effectieve brekingsindex n . verkrijgen _eff = k _SPP /k ₀ = Re(n _eff ) + i Im(n _eff ) van de voorgestelde plasmonische golfgeleider. Voor de zeer beperkte plasmonische golfgeleidermodi, het reële deel van de effectieve brekingsindex Re(n _eff ) beschrijven ruwweg de modusbeperking, terwijl het denkbeeldige deel Im(n _eff ) is recht evenredig met het voortplantingsverlies van de modus:de grotere Re(n _eff ) is, hoe hoger de opsluiting. Wanneer g groot genoeg is zodat tanh[g (k _SPP ² − ε _r k ₀ ² /ε ₀ )] ~ 1, Vgl. (1) zou worden teruggebracht tot de spreidingsrelatie

die de plasmonische golfgeleidermodus weergeeft die wordt ondersteund door een enkele laag BDS alleen. De complexe geleidbaarheid van BDS wordt gepresenteerd in methoden Eqs (3)–(4).

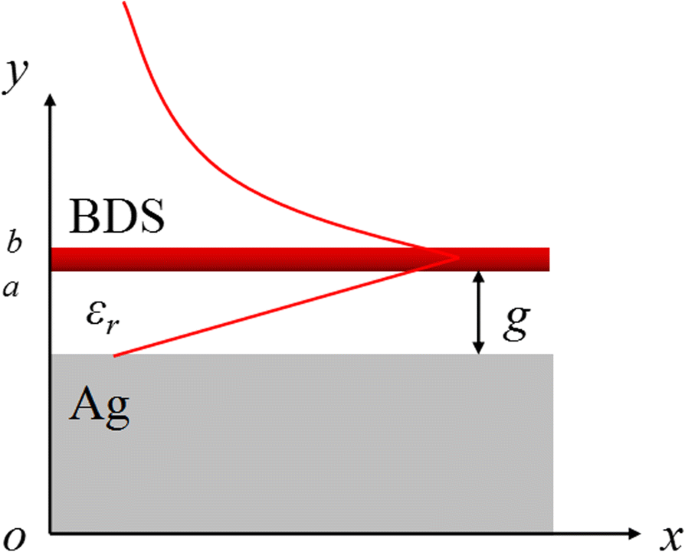
Schematische weergave van de BIM plasmonische golfgeleider:een monolaag BDS-film wordt geplaatst op een spleetbreedte g weg van het zilveren substraat gescheiden door een diëlektrische afstandhouder met permittiviteit ε _r . De TM-gepolariseerde plasmonische golfgeleidermodus plant zich voort langs de x richting en vervalt langs de y richting. Schematische weergave van de E _x distributie wordt weergegeven door de rode lijn

Resultaten en discussie

Eerst demonstreren we de afhankelijkheid van de modusbeperking en het voortplantingsverlies van de BIM-golfgeleider op de BDS-metaalspleetbreedte g en Fermi-energie E _F . Door E . te nemen _F = 70 meV, we berekenen de effectieve brekingsindices van de SPP-golfgeleidermodus n _eff voor verschillende waarden van g , waar de echte en denkbeeldige delen, Re(n _eff ) en Im(n _eff ), zijn respectievelijk uitgezet in Fig. 2a, b. Zoals weergegeven in figuur 2a, zijn de curven voor g = 10 en 100 m fuseren bij frequenties hoger dan 0,05 THz, wat suggereert dat de plasmonische golfgeleidermodi zo nauw zijn opgesloten in de BDS-isolatorinterface dat de meeste SPP-velden worden verdeeld binnen de schaal van 10 μm en het zilver niet zou werken bij zo'n grote spleetbreedte. Terwijl de modusbeperking drastisch wordt verbeterd na de spleetbreedte g wordt geleidelijk verminderd van 1 μm, hoe kleiner g onderzoeken, en de sterkere opsluiting kan worden verkregen. De vergelijkbare tendens kan worden waargenomen in de afhankelijkheid van voortplantingsverlies van de spleetbreedte g , zoals afgebeeld in Fig. 2b. Aan de andere kant, voor een vaste spleetbreedte kleiner dan 1 μm, Re(n _eff ) elk vertoont aanvankelijk een uitgesproken reductie tot een minimum en vertoont vervolgens een geleidelijk toenemend gedrag, terwijl Im(n _eff ) neemt elk monotoon af naarmate de frequentie toeneemt. Er is dus een geoptimaliseerd frequentiegebied waar de modusbeperking sterk wordt verbeterd terwijl het voortplantingsverlies geleidelijk wordt verminderd. Deze eigenschap is zelden waargenomen in traditionele plasmonische golfgeleidermodi op de metaal-isolatorinterface. Afbeelding 2c, d geeft de afhankelijkheid weer van de modusopsluiting en het voortplantingsverlies van de Fermi-energie E _F van de BDS-film, waarbij de spleetbreedte g = 1 μm. Vergelijkbaar met het geval van een monolaag en dubbellaagse golfgeleider, nemen de modusopsluiting en het voortplantingsverlies continu af met de toename van Fermi-energie, wat kan worden toegeschreven aan de verbeterde metalliciteit en verlengde dragerrelaxatietijd van BDS. De beperkingsfactor van de plasmonische golfgeleidermodus bij 2,5 THz kan bijvoorbeeld oplopen tot λ ₀ /15, waar is λ ₀ de invallende golflengte, met een relatief laag verlies van 1,0 dB/λ ₀ wanneer de BDS-metaalspleetbreedte 10 nm is en de Fermi-energie 70 meV is. Daarom zou het vertrouwen op kaders die hierboven al zijn besproken, modusbeperking verhogen met een relatief laag verlies, wat kan worden gebruikt voor het ontwerp van geïntegreerde optische filters, buffers en Mach-Zehnder-interferometer.

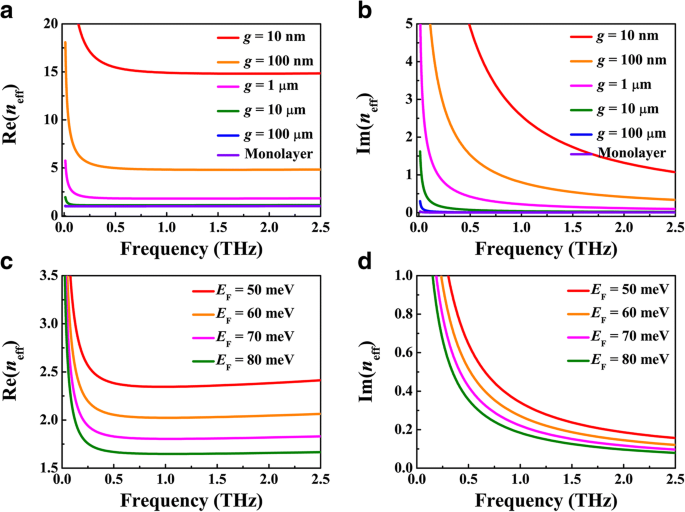
Reële en denkbeeldige delen van de effectieve brekingsindex n _eff voor een , b verschillende spleetbreedte g , waarbij de Fermi-energie van BDS is vastgesteld op E _F = 70 meV, en c , d verschillende waarden van de Fermi-energie E _F , waarbij de spleetbreedte is vastgesteld op g = 1 μm

Om bovengenoemde analyse te onderzoeken, voeren we numerieke berekeningen uit over de transmissie-intensiteit en veldverdeling van de voorgestelde golfgeleiderstructuur. De simulatie-instelling wordt beschreven in methoden. Vergelijking met de monolaag BDS-golfgeleider met dezelfde Fermi-energie E _F = 70 meV, de transmissie-intensiteit van de BIM-golfgeleider bij de frequentie van 1,56 THz is 0,97, wat hoger is dan die van de eerste, zoals weergegeven in figuur 3a, wat suggereert dat de plasmonische golfgeleidermodus in de BIM-structuur een lager voortplantingsverlies heeft. Aan de andere kant, zoals aangegeven in figuur 2a, is het reële deel van de effectieve brekingsindex van BIM bij 1,56 THz Re(n _eff ) = 2,45, wat veel hoger is dan dat van het monolaag geval van 1.002. Om deze verklaring te visualiseren, wordt het magnetische veld Hz distributies van deze modi worden weergegeven in Fig. 3b, c. Het kan duidelijk worden gevonden dat de zeer beperkte plasmonische modus in BIM-golfgeleider een kortere oscillatieperiode vertoont dan die van het monolaag BDS-geval. Bovendien is het grootste deel van het plasmonveld gelokaliseerd in zo'n smalle spleet ~ λ ₀ /2000, dat veelbelovende toepassingen bevat in near-field enhancement voor niet-lineaire fysica.

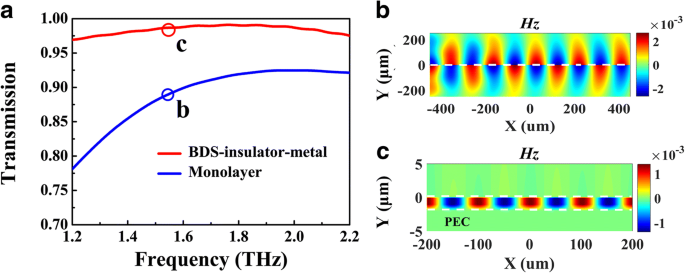
Numerieke berekeningen van de transmissiespectra (a ) en magnetisch veld (H _z ) distributies (b , c ) van BIM (rode curve) en monolaag (blauwe curve) golfgeleiders, waarbij E _F = 70 meV, g = 50 μ m, en incidentfrequentie van 1,56 THz

Van alle bovengenoemde toepassingen is optische resonator het essentiële element voor het afstemmen van de THz-plasmonische golfgeleidermodus. Zoals geïllustreerd in Fig. 4a, twee silicium (n _Si = 3.4) [24] linten zijn ingebed in de diëlektrische afstandhouder om de reflecterende spiegels te vormen, waar de zich voortplantende plasmonische golf heen en weer kan worden gereflecteerd op het silicium-lucht-interface, waardoor gelokaliseerde staande golfresonantie wordt gevormd in het BIM-gebied tussen de twee siliciumlinten . Alleen de invallende frequentie voldoet aan de resonantieconditie van de staande golf, de plasmonische golven kunnen via koppeling met de ontworpen optische resonator naar de uitgang van de golfgeleider zenden. Figuur 4a toont het transmissiespectrum van de BIM-golfgeleider met twee siliciumlinten, waar twee transmissiepieken met FWHM-waarden (volledige breedte op half maximum) van 0,12 en 0,09 THz duidelijk te vinden zijn bij de frequenties van 1,56 en 2,22 THz, wat nieuwe banddoorlaatfiltereffect in het terahertz-gebied. De magnetische veldverdelingen (|H _z |² ) van de transmissiepieken zijn weergegeven in figuur 4c, e, wat impliceert dat het BIM-gebied dat is ingeklemd tussen twee siliciumlinten, kan worden beschouwd als een Fabry-Perot (FP) -holte. De resonantie van de eerste en tweede orde is duidelijk te vinden in de FP-holte. De invallende plasmonische golf nabij de resonantiefrequentie kan in de FP-holte worden gekoppeld en vervolgens door de BIM-golfgeleider worden verzonden, die de transmissiepiek in het spectrum genereert. Terwijl voor het niet-resonante frequentiegebied de staande golf niet kan worden gevormd en dus de invallende golven zijn verboden in de linkerpoort van de BIM-golfgeleider, zoals weergegeven in figuur 4d. Bovendien, in combinatie met de dispersierelatie van BIM-golfgeleider, kan de transmissie-intensiteit analytisch worden berekend door de gekoppelde modustheorie (CMT) [17]:

$$ T\left(\omega \right)=\frac{\kappa_w^2}{{\left(\omega -{\omega}_0\right)}^2-{\left({\kappa}_w+{ \kappa}_i\right)}^2}, $$ (5)

waar ω ₀ is respectievelijk de resonantiefrequentie van de FP-holte. Hier, κ _w = ω ₀ /(2Q _w ) en κ _ik = ω ₀ /(2Q _ik ) zijn vervalsnelheden gerelateerd aan respectievelijk het verlies van de golfgeleiderkoppeling en het intrinsieke verlies van de FP-holte. De kwaliteitsfactor voor totaal en intrinsiek verlies kan worden geschat met Q _t = ω ₀ /FWHM, en Q _oi = − Re(n _eff )/(2Im(n _eff )), respectievelijk. Vervolgens kan de kwaliteitsfactor voor golfgeleiderkoppelingsverlies worden verkregen door het intrinsieke verlies af te trekken van het totale verlies, namelijk Q _ei = Q _oi V _ti /(Q _oi − Q _ti ) [17]. De analytische resultaten op basis van CMT komen goed overeen met de numerieke simulaties, zoals weergegeven in figuur 4b.

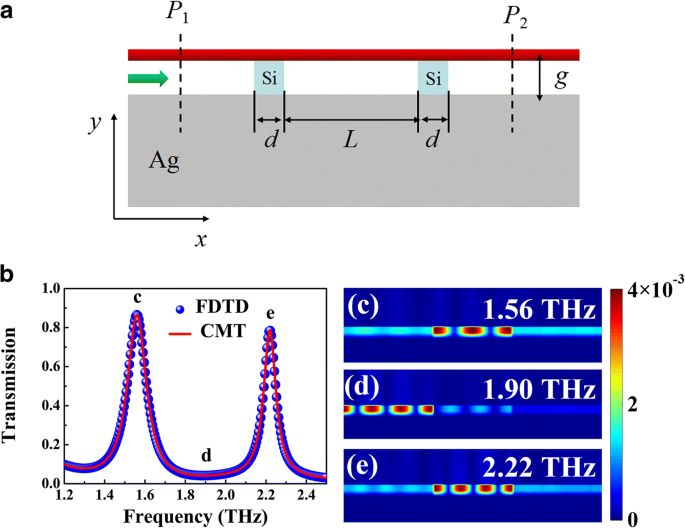
een Schema van de BIM-golfgeleider met geïntroduceerde siliconenlinten. De breedte van elk siliciumlint is d , en de afstand tussen de linten is L . b Numerieke (blauwe ballen) en CMT-aangepaste (rode curve) transmissiespectra van de voorgestelde structuur waarbij g = 1 μm, d = 5 μm, en L = 120 μm. c –e Magnetische veldverdelingen (|H _z |² ) of bij de incidentfrequenties van 1,56 (c ), 1,90 (d ), en 2,22 THz (e )

Afbeelding 5 toont de afhankelijkheid van de resonantiefrequentie van de holtelengte L , waar g = 1 μm, d = 5 μm, en E _F = 70 meV. De transmissiepiek heeft de neiging naar rood te verschuiven met de toename van L , zoals weergegeven in figuur 5a, die verder kan worden beschreven door de staande golfresonantietoestand 2k _SPP (ω _r )L + θ = 2mπ (m = 1, 2, 3, ...), waarbij θ is de reflecterende faseverschuiving van de silicium-lucht-interface en k _SPP (ω _r ) is de golfvector van BIM-golfgeleider bij resonantiefrequentie. Zoals weergegeven in figuur 5b, vertonen de resonantiefrequenties van de eerste en tweede modus inderdaad een roodverschuiving met de toename van L . Volgens vgl. (1), de modusbeperking wordt beïnvloed door de spleetbreedte g die dus invloed hebben op de resonantiefrequentie. Afbeelding 6a geeft de transmissiespectra weer voor verschillende g , waar L = 120 μm en E _F = 70 meV. Met de toename van g , vertoont de resonantiepiek in dezelfde volgorde een blauwverschuiving. Dit fenomeen kan worden toegeschreven aan de dramatische afname van Re(n _eff ) zoals weergegeven in Fig. 6c. De afstemming van Fermi-energie van BDS kan worden gerealiseerd door middel van alkalische oppervlaktedoping in experiment. Figuur 6b geeft de transmissiespectra weer voor verschillende Fermi-energie, waarbij de andere parameters hetzelfde zijn als in figuur 4b. Naarmate de Fermi-energie toeneemt, vertoont de transmissiepiek een blauwverschuiving, die ook betrokken kan zijn bij het staande golfresonantiebeeld. Voor een vaste lengte L , de FP-holte ondersteunt de resonantie met gedefinieerde SPP-golflengte λ _SPP = λ ₀ / Re(n _eff ), waar λ ₀ is de invallende golflengte. Zoals weergegeven in Fig. 6c, Re(n _eff ) wordt verminderd met de toename van Fermi-energie. Als resultaat is de invallende golflengte λ ₀ moet ook worden verlaagd om λ . te behouden _SPP als een constante. Dat is de reden waarom de transmissiepiek de neiging heeft naar blauw te verschuiven met de toename van Fermi-energie. Ondertussen wordt de bandbreedte van de transmissiepiek versmald, wat kan worden toegeschreven aan de afname van Im(n _eff ), d.w.z. het voortplantingsverlies van de plasmonische golfgeleidermodus in BIM-golfgeleider.

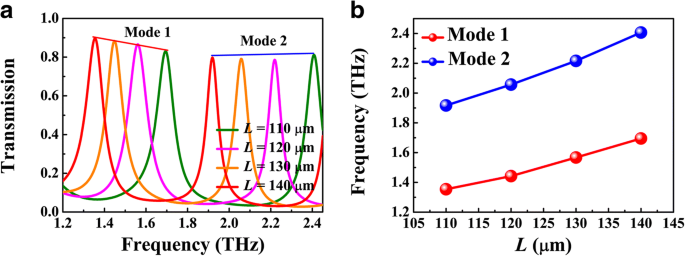
een Numerieke transmissiespectra voor verschillende holtelengtes L . b Resonantiefrequenties van modi 1 en 2 als functies van de holtelengte L . Hier, g = 1 μm, d = 5 μm, en E _F = 70 meV

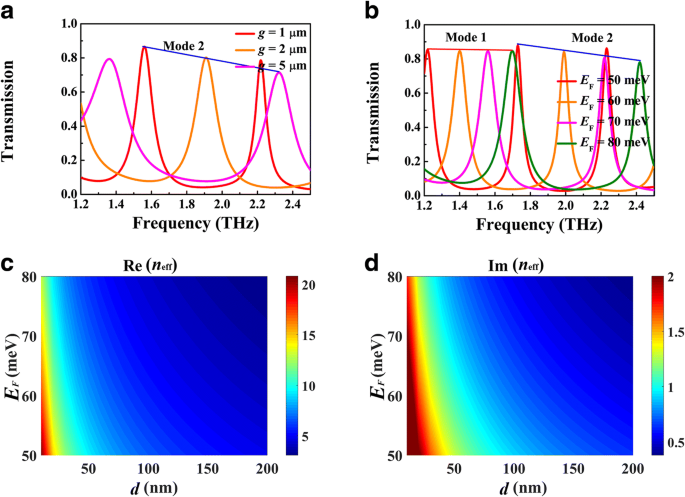
Transmissiespectra voor verschillende spleetbreedtes g (een ) en Fermi-energie E _F (b ), waarbij de andere parameters hetzelfde zijn als in Fig. 4b. Afhankelijkheid van Re(n _eff ) (c ) en Im(n _eff ) (d ) op de Fermi-energie E _F en tussenruimte g

Conclusies

Samenvattend hebben we de zeer beperkte terahertz-plasmonische modus aangetoond, ondersteund door een BIM-golfgeleider. De modusopsluiting en verlieskarakteristieken zijn besproken met de variaties van BDS-metaalscheiding en Fermi-energie, wat aangeeft dat er een geoptimaliseerd frequentiebereik is met verbeterde modusopsluiting en verminderd voortplantingsverlies, wat zelden is gemeld in de traditionele SPP-modus in metalen structuur. Anders dan de eerder bestudeerde op BDS gebaseerde structuur, kan de modus van deze BIM-golfgeleider efficiënt worden ondersteund in een zeer smalle spleet met een breedte kleiner dan λ ₀ /2000. Door twee siliciumlinten als reflecterende spiegels te nemen, is een dynamisch afstembaar banddoorlaatfilter bereikt, waar de resonantiefrequentie actief kan worden geregeld door de Fermi-energie van BDS-film aan te passen zonder de structurele parameters opnieuw te optimaliseren.

Methoden

Numerieke resultaten worden verkregen door gebruik te maken van de 2D-methode met eindig verschil in tijddomein (FDTD), waarbij de perfect op elkaar afgestemde lagen het verstrooide licht in de x absorberen en y routebeschrijving. De maaswijdte van de BDS-film is ingesteld als dx × dy = 1 μm × 0,02 μm om een goede convergentie te bereiken.

De frequentieafhankelijke geleidbaarheid van BDS wordt beschreven door de Kubo-formule met willekeurige fasebenadering [12, 25].

$$ \operatornaam{Re}\sigma \left(\Omega \right)=\frac{e^2}{\mathrm{\hslash}}\frac{tk_F}{24\pi}\Omega G\left(\ Omega /2\right), $$ (3) $$ \operatorname{Im}\sigma \left(\Omega \right)=\frac{e^2}{\mathrm{\hslash}}\frac{tk_F} {24{\pi}^2}\left\{\frac{4}{\Omega}\left[1+\frac{\pi^2}{3}{\left(\frac{T}{E_F} \right)}^2\right]+8\Omega {\int}_0^{\varepsilon_c}\left[\frac{G\left(\varepsilon \right)-G\left(\Omega /2\right) }{\Omega^2-4{\varepsilon}^2}\right]\varepsilon d\varepsilon \right\}, $$ (4)

waar G (E ) = n (−E ) − n (E ) en n (E ) is de Fermi-Dirac-verdelingsfunctie, E _F is de Fermi-energie van BDS, k _F = E _F /ћv _F is het Fermi-momentum, en v _F = 10⁶ m/s is de Fermi-snelheid. ε = E/E _F , Ω = ћω/E _F + iћτ ⁻¹ /E _F , waar ћτ ⁻¹ = v _F /(k _F μ ) is de elektronenverstrooiingssnelheid die sterk afhankelijk is van de dragermobiliteit μ. _c = E _c /E _F (E _c is de afsnijenergie waarboven het Dirac-spectrum niet langer lineair is), en t is de kwantumdegeneratiefactor. Als we AlCuFe als voorbeeld nemen, worden de aanpasparameters in onze berekeningen als volgt ingesteld:t = 40, ε _c = 3, μ = 3 × 10⁴ cm² V⁻¹ s⁻¹ en E _F = 70 meV.

Bij dit onderzoek zijn geen menselijke deelnemers, gegevens of weefsels of dieren betrokken.

Afkortingen

BDS:: Bulk Dirac halfmetalen
BIM:: BDS-isolator-metaal
CMT:: Gekoppelde modustheorie
FDTD:: Tijdsdomein met eindig verschil
FWHM:: Volledige breedte op halve maximum
SPP's:: Oppervlakte plasmon polaritonen

In situ elektrospinning op jodium gebaseerde vezelachtige gazen voor antibacterieel wondverband Een functionele PPy/ZnO-tussenlaag om de elektrochemische prestaties van lithium-/zwavelbatterijen te verbeteren

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal