MATLAB - Differentieel
MATLAB biedt de diff commando voor het berekenen van symbolische afgeleiden. In zijn eenvoudigste vorm geef je de functie die je wilt differentiëren door aan het diff-commando als argument.
Laten we bijvoorbeeld de afgeleide berekenen van de functie f(t) =3t 2 + 2t -2
Voorbeeld
Maak een scriptbestand en typ de volgende code erin −
syms t f = 3*t^2 + 2*t^(-2); diff(f)
Wanneer de bovenstaande code wordt gecompileerd en uitgevoerd, levert dit het volgende resultaat op −
ans = 6*t - 4/t^3
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave voert de code uit en geeft het volgende resultaat −
ans = -(4.0)*t^(-3.0)+(6.0)*t
Verificatie van elementaire differentiatieregels
Laten we kort verschillende vergelijkingen of regels voor differentiatie van functies noemen en deze regels verifiëren. Hiervoor schrijven we f'(x) voor een afgeleide van de eerste orde en f"(x) voor een afgeleide van de tweede orde.
Hieronder volgen de regels voor differentiatie −
Regel 1
Voor alle functies zijn f en g en alle reële getallen a en b de afgeleide van de functie −
h(x) =af(x) + bg(x) met betrekking tot x wordt gegeven door −
h'(x) =af'(x) + bg'(x)
Regel 2
De som en aftrekken regels stellen dat als f en g twee functies zijn, f' en g' respectievelijk hun afgeleiden zijn, dan
(f + g)' =f' + g'
(f - g)' =f' - g'
Regel 3
Het product regel stelt dat als f en g twee functies zijn, f' en g' respectievelijk hun afgeleiden zijn, dan
(f.g)' =f'.g + g'.f
Regel 4
Het quotiënt regel stelt dat als f en g twee functies zijn, f' en g' respectievelijk hun afgeleiden zijn, dan
(f/g)' =(f'.g - g'.f)/g 2
Regel 5
De polynoom of elementaire machtsregel stelt dat, als y =f(x) =x n , dan f' =n. x (n-1)
Een direct resultaat van deze regel is dat de afgeleide van elke constante nul is, d.w.z. als y =k , een constante, dan
f' =0
Regel 6
De keten regel stelt dat, afgeleide van de functie van een functie h(x) =f(g(x)) met betrekking tot x is,
h'(x)=f'(g(x)).g'(x)
Voorbeeld
Maak een scriptbestand en typ de volgende code erin −
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
Wanneer u het bestand uitvoert, geeft MATLAB het volgende resultaat weer −
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave voert de code uit en geeft het volgende resultaat −
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
Afgeleiden van exponentiële, logaritmische en goniometrische functies
De volgende tabel geeft de afgeleiden van veelgebruikte exponentiële, logaritmische en trigonometrische functies −
| Functie | Afgeleide |
|---|---|
| c a.x | c a.x .ln c.a (ln is natuurlijke logaritme) |
| e x | e x |
| ln x | 1/x |
| lnc x | 1/x.ln c |
| x x | x x .(1 + ln x) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | sec 2 (x), of 1/cos 2 (x), of 1 + tan 2 (x) |
| kinderbed(x) | -csc 2 (x), of -1/sin 2 (x), of -(1 + kinderbed 2 (x)) |
| sec(x) | sec(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
Voorbeeld
Maak een scriptbestand en typ de volgende code erin −
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
Wanneer u het bestand uitvoert, geeft MATLAB het volgende resultaat weer −
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave voert de code uit en geeft het volgende resultaat −
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
Hogere-ordederivaten berekenen
Om hogere afgeleiden van een functie f te berekenen, gebruiken we de syntaxis diff(f,n) .
Laten we de tweede afgeleide van de functie berekenen y =f(x) =x .e -3x
f = x*exp(-3*x); diff(f, 2)
MATLAB voert de code uit en geeft het volgende resultaat −
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave voert de code uit en geeft het volgende resultaat −
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
Voorbeeld
Laten we in dit voorbeeld een probleem oplossen. Gegeven dat een functie y =f(x) =3 sin(x) + 7 cos(5x) . We zullen moeten uitzoeken of de vergelijking f" + f =-5cos(2x) klopt.
Maak een scriptbestand en typ de volgende code erin −
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Wanneer u het bestand uitvoert, wordt het volgende resultaat weergegeven −
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave voert de code uit en geeft het volgende resultaat −
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
De maxima en minima van een curve vinden
Als we zoeken naar de lokale maxima en minima voor een grafiek, zoeken we in feite naar de hoogste of laagste punten in de grafiek van de functie op een bepaalde plaats, of naar een bepaald bereik van waarden van de symbolische variabele.
Voor een functie y =f(x) worden de punten op de grafiek waar de grafiek een helling nul heeft, stationaire punten genoemd . Met andere woorden, stationaire punten zijn waar f'(x) =0.
Om de stationaire punten van een functie die we differentiëren te vinden, moeten we de afgeleide gelijk aan nul stellen en de vergelijking oplossen.
Voorbeeld
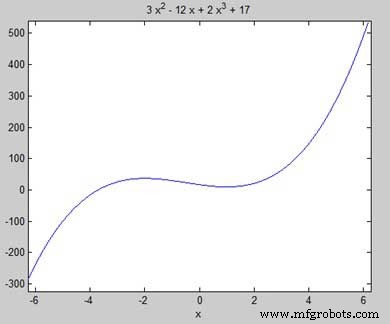
Laten we de stationaire punten van de functie f(x) =2x 3 . vinden + 3x 2 − 12x + 17
Voer de volgende stappen uit −
Laten we eerst de functie invoeren en de grafiek tekenen.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB voert de code uit en geeft de volgende plot terug −
Hier is Octave-equivalente code voor het bovenstaande voorbeeld −
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
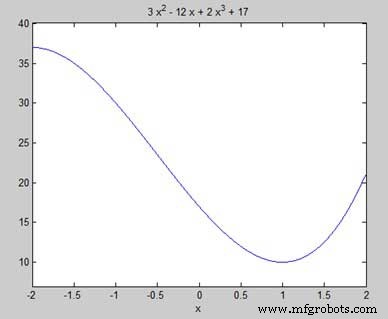
Ons doel is om lokale maxima en minima in de grafiek te vinden, dus laten we de lokale maxima en minima zoeken voor het interval [-2, 2] in de grafiek.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB voert de code uit en geeft de volgende plot terug −
Hier is Octave-equivalente code voor het bovenstaande voorbeeld −
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
Laten we vervolgens de afgeleide berekenen.
g = diff(y)
MATLAB voert de code uit en geeft het volgende resultaat −
g = 6*x^2 + 6*x - 12
Hier is het Octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave voert de code uit en geeft het volgende resultaat −
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
Laten we de afgeleide functie g oplossen om de waarden te krijgen waar het nul wordt.
s = solve(g)
MATLAB voert de code uit en geeft het volgende resultaat −
s = 1 -2
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave voert de code uit en geeft het volgende resultaat −
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
Dit komt overeen met onze plot. Laten we dus de functie f evalueren op de kritische punten x =1, -2. We kunnen een waarde in een symbolische functie vervangen door de subs . te gebruiken commando.
subs(y, 1), subs(y, -2)
MATLAB voert de code uit en geeft het volgende resultaat −
ans = 10 ans = 37
Het volgende is het octaaf-equivalent van de bovenstaande berekening −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
Daarom, De minimum- en maximumwaarden van de functie f(x) =2x 3 + 3x 2 − 12x + 17, in het interval [-2,2] zijn 10 en 37.
Differentiaalvergelijkingen oplossen
MATLAB biedt de dsolve commando voor het symbolisch oplossen van differentiaalvergelijkingen.
De meest eenvoudige vorm van de dsolve commando voor het vinden van de oplossing van een enkele vergelijking is
dsolve('eqn')
waar eqn is een tekenreeks die wordt gebruikt om de vergelijking in te voeren.
Het retourneert een symbolische oplossing met een set willekeurige constanten die MATLAB C1, C2 enzovoort noemt.
U kunt ook begin- en randvoorwaarden voor het probleem specificeren, als door komma's gescheiden lijst na de vergelijking als −
dsolve('eqn','cond1', 'cond2',…)
Om de opdracht dsolve te gebruiken, worden afgeleiden aangegeven met een D . Een vergelijking als f'(t) =-2*f + kosten(t) wordt bijvoorbeeld ingevoerd als −
'Df =-2*f + cos(t)'
Hogere afgeleiden worden aangegeven door D te volgen in de volgorde van de afgeleide.
De vergelijking f"(x) + 2f'(x) =5sin3x moet bijvoorbeeld worden ingevoerd als −
'D2y + 2Dy =5*sin(3*x)'
Laten we een eenvoudig voorbeeld nemen van een differentiaalvergelijking van de eerste orde:y' =5y.
s = dsolve('Dy = 5*y')
MATLAB voert de code uit en geeft het volgende resultaat −
s = C2*exp(5*t)
Laten we een ander voorbeeld nemen van een differentiaalvergelijking van de tweede orde als:y" - y =0, y(0) =-1, y'(0) =2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB voert de code uit en geeft het volgende resultaat −
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB



