Thermo-elektrisch effect in een gecorreleerde Quantum Dot zijdelings gekoppeld aan Majorana-gebonden staten

Abstract

We bestuderen theoretisch het thermo-elektrische effect in een hybride apparaat dat bestaat uit een topologische halfgeleidende nanodraad die Majorana-gebonden toestanden (MBS's) host en een kwantumdot (QD) verbonden met de linker en rechter niet-magnetische elektroden die op verschillende temperaturen worden gehouden. De elektron-elektron Coulomb-interacties in de QD worden in aanmerking genomen door de niet-evenwichtsfunctietechniek van Green. We vinden dat de tekenverandering van de thermokracht, die nuttig is voor het detecteren van de MBS's, zal plaatsvinden door de QD-MBS-hybridisatiesterkte, de directe overlap tussen de MBS's aan de tegenovergestelde uiteinden van de nanodraad en de systeemtemperatuur te veranderen. Grote waarde van 100% spin-gepolariseerde of pure spin-thermokracht ontstaat zelfs bij afwezigheid van Zeeman-splitsing in de QD of magnetische elektroden, omdat de MBS's zijn gekoppeld aan elektronen van slechts één bepaalde spinrichting in de QD vanwege de chirale aard van de Majorana fermionen. Bovendien zal de omvang van de thermokracht duidelijk worden vergroot door het bestaan van MBS'en.

Inleiding

De voorbereiding en detectie van nul-energie Majorana-gebonden toestanden (MBS's) zijn van bijzonder belang in de moderne fysica van de gecondenseerde materie. Fundamenteel zijn de MBS's een vaste-stof-tegenhanger van Majorana-fermionen en worden ze geassocieerd met niet-Abelse statistieken die topologisch beschermde kwantuminformatie mogelijk maken met potentiële toepassingen in kwantumberekening zonder decoherentie [1-3]. Afgezien hiervan zijn de MBS's ook veelbelovend in het ontwerp van zeer efficiënte elektronische apparaten, zoals de spintronica [4]. Goed gescheiden MBS's kunnen in verschillende systemen worden gemaakt, waarvan de belangrijkste schema's niet-centrosymmetrische supergeleiders [5], drie- of tweedimensionale topologische isolatoren gekoppeld aan supergeleiders [6], elektrostatische defecten in topologische supergeleiders [7], p-golf supergeleiders [8], de halfgeleidende [9] of ferromagnetische [10] nanodraden met native sterke spin-baan interactie proximitatie tot conventionele s-golf supergeleiders, en Josephson-juncties [11].

Wat betreft de detectie van MBS's, het is ook behoorlijk uitdagend omdat de Majorana-fermionen hun eigen antideeltjes zijn en ladingsneutraal zijn vanwege hun intrinsieke symmetrie tussen deeltjes en gaten. Er zijn verschillende experimenten uitgevoerd om het bestaan van MBS's te verifiëren door middel van verschijnselen zoals de 4π periodieke Josephson-stroomfase in juncties tussen topologische supergeleiders [12], halfgetalen geleidingsplateau op het coërcitiefveld in een hybride structuur bestaande uit topologische supergeleiders en topologische kwantumafwijking Hall-isolator [13], tunnelspectroscopie met behulp van Rashba-nanodraden gekoppeld aan de bulk s -golf supergeleiders [14], en nul bias van de differentiële geleiding aan de randen van de draden [14, 15]. Deze verschijnselen hebben echter een andere mogelijke fysieke oorsprong, behalve MBS's, en er zijn toen alternatieve schema's voorgesteld. Een daarvan is de hybridisatie van MBS's met andere nanoschaalstructuren, zoals de nuldimensionale kwantumdot (QD) waarin de energieniveaus, elektron-elektron Coulomb-interacties, deeltjesaantallen en koppelingssterkte met de externe omgeving allemaal goed controleerbaar zijn [ 16, 17]. Bij lage temperatuur werd theoretisch een halfmaximale geleiding voorspeld wanneer het energieniveau van de QD is uitgelijnd met de Fermi-energie in de leads als een duidelijk bewijs van de vorming van een paar MBS's [18]. Dit resultaat wordt onveranderd aangevuld door de aanpassing van het QD-energieniveau [19] en is met succes waargenomen in een experiment in een QD gekoppeld aan een InAs-Al nanodraad [20]. Onlangs werden optische schema's op basis van QD-structuur ook theoretisch voorgesteld om de MBS's te detecteren met behulp van optische pomp-sondetechniek. [21, 22] In ring- of T-vormige QD-gebaseerde systemen worden de kwantuminterferentieverschijnselen drastisch beïnvloed door de MBS's [23-25] en kunnen ze vervolgens worden gebruikt voor het detectieschema met behulp van bijvoorbeeld de Fano-effect [26–28].

Onlangs is er ook wat werk verricht met betrekking tot de detectie van de MBS's via thermo-elektrisch effect, dat zich richt op de conversie tussen elektrische en thermische energieën. Dit oude onderzoeksonderwerp krijgt hernieuwde aandacht vanwege de snelle vooruitgang van de groei en fabricage van mesoscopische apparaten en nanostructuren, waarbij de thermo-elektrische prestaties duidelijk zijn verbeterd [29, 30]. Zeer efficiënte energieoogsters op basis van QD's die zijn gedefinieerd op bijvoorbeeld een GaAs/AlGaAs-interface tweedimensionaal elektronengas zijn recentelijk gerapporteerd [31, 32]. Versterking van het thermo-elektrische effect daarin kan worden toegeschreven aan de aanzienlijke vermindering van de thermische geleidbaarheid door grensverstrooiing en de optimalisatie van de elektrische transporteigenschappen die uniek zijn in deze laagdimensionale systemen [30-32]. De thermokracht (Seebeck-coëfficiënt) is de centrale grootheid in thermo-elektrisch effect. Het is de sterkte van een nullastspanning als reactie op een temperatuurgradiënt toegepast in een vast materiaal met vrije elektronische dragers. Hou et al. theoretisch voorspeld dat de thermokracht tussen een QD en supergeleider die een Majorana-randtoestand host, voldoet aan de Mott-formule en in het algemeen niet verdwijnt door gebruik te maken van het Landauer-Büttiker-formalisme [33]. Op basis van een dergelijke eigenschap kan men de temperatuur van de Majorana-randtoestand afleiden door de differentiële geleidbaarheid en het thermovermogen te meten. Leijnse demonstreerde theoretisch dat de koppeling tussen een QD met afstembaar energieniveau en MBS's de symmetrie tussen deeltjes en gaten verbreekt, en de veranderingen van thermokracht bieden een nieuwe manier om het bestaan van Majorana-toestanden te bewijzen [34]. De thermo-elektrische eigenschappen in een dergelijke opstelling kunnen ook worden gebruikt om de temperatuur van de supergeleider te detecteren en om informatie te extraheren over het dissipatieve verval van MBS's [34]. In een structuur met een QD gekoppeld aan twee elektroden, López et al. toonde aan dat de thermokracht zijn teken zal veranderen door de directe hybridisatie tussen de MBS's te veranderen, een goed bewijs van het bestaan van MBS's [35]. De tekenverandering van de thermokracht werd vervolgens ook gevonden in systemen van een QD met twee [36] of drie [37] elektroden. Bovendien werd aangetoond dat de relatie tussen de schotruis en thermo-elektrische grootheden een puur elektrische manier kan zijn om de ladingsneutrale MBS's te detecteren [38, 39].

In het huidige artikel stellen we een gehybridiseerd systeem voor dat bestaat uit MBS's en een QD gekoppeld aan elektroden (zie Fig. 1) om de eigenschappen van de thermokracht te bestuderen. In het nanosysteem dat we hebben overwogen, wordt rekening gehouden met de sterke Coulomb-interactie in de stip, die in eerdere werken is verwaarloosd [18, 22-24, 34-39]. Verder zijn we van mening dat slechts één spincomponent van de QD-spin gekoppeld is aan de MBS's vanwege de chirale aard van de MBS's [40]. We vinden dat het teken van de thermokracht effectief kan worden omgekeerd door de dot-MBS-koppelingssterkte, de directe hybridisatie tussen de MBS's en de systeemtemperatuur te veranderen. De resulterende grote 100% spin-gepolariseerde en pure spin-thermokracht, die de overeenkomstige 100% spin-gepolariseerde en pure spinstromen in een gesloten circuit zijn, zijn nuttig in spintronica. De koppeling van beide MBS's aan de QD zal de omvang van de thermokracht verder vergroten, maar verandert de essentiële resultaten niet wanneer slechts één van de MBS's aan de punt is gekoppeld. Op basis van de momenteel geavanceerde kwantumtransportmetingen voor de MBS's via QD in combinatie met topologische supergeleidende nanodraden, denken we dat ons voorstel in de toekomst experimenteel kan worden getest. Bovendien kunnen ons voorstel en onze bevindingen in dit werk een uitstekende manier zijn om de vorming van de MBS's in QD te detecteren.

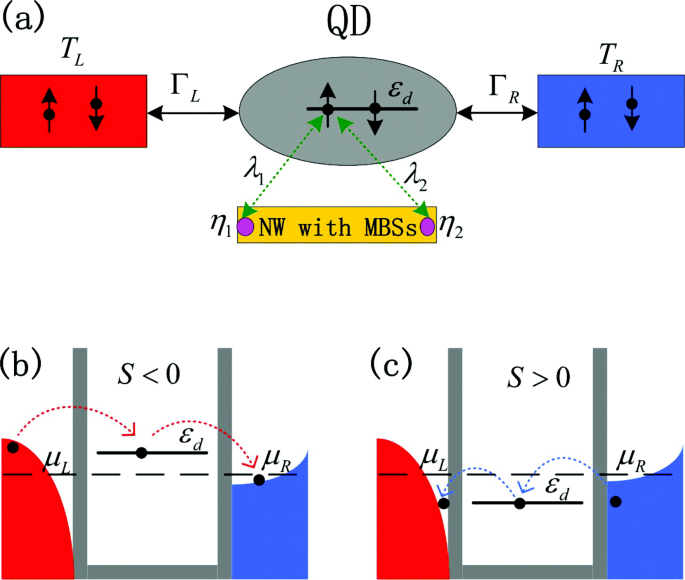
Schema van het model (kleur online). een Schema van de simulatiestructuur samengesteld door een QD met gate-afstembaar energieniveau ε _d die kan worden ingenomen door een spin-up of een spin-down elektron. De QD is verbonden met de linker- en rechterkabels die op verschillende temperaturen worden gehouden met een koppelingssterkte Γ _{L /R} . De MBS'en η _1/2 worden gevormd in de uiteinden van de halfgeleidende nanodraad en zijn gekoppeld aan de spin-up elektronen in de QD vanwege de chirale aard van de Majorana-fermionen met een sterkte van λ ₁ en λ ₂ , respectievelijk. De energietoestand van spin-up elektronen zal worden veranderd door MBSs-QD-koppeling, en vervolgens de sterkte en het teken van de thermokracht S zal worden beïnvloed. In het huidige model gaan we uit van de temperatuur van de linker lead T _L hoger is dan die van de rechter T _R , en dan zijn er meer elektronen (lege toestanden) die boven (onder) de chemische potentiaal in de linkerdraad worden geëxciteerd dan die in de rechterdraad. b , c De elektronentunnelprocessen en de resulterende thermokracht in afwezigheid van MBSs-QD-koppeling. In b , het QD-energieniveau ε _d is boven de chemische potentiaal van de leads μ _{L /R} =μ , en dan elektronen uit de bezette toestanden ε _d>μ in de linker warmere afleiding zal tunnelen door puntstatus ε _d naar de lege toestand in de rechter koudere leiding, wat resulteert in een negatieve thermopopwer S <0. In c , ε _d <μ , en dan wordt het teken van de thermokracht dienovereenkomstig omgekeerd

Model en methoden

De effectieve Hamiltoniaan van de QD gekoppeld aan MBS's en de linker en rechter normale metalen elektroden heeft de volgende vorm [34, 35]:

$$\begin{array}{@{}rcl@{}} H &=\sum_{k\beta\sigma}\varepsilon_{k\beta}c_{k\beta\sigma}^{\dag}c_{ k\beta\sigma} +\sum_{\sigma}\varepsilon_{d}d_{\sigma}^{\dag}d_{\sigma}+Ud_{\uparrow}^{\dag} d_{\uparrow} d_ {\downarrow}^{\dag} d_{\downarrow} \\ &+\sum_{k\beta\sigma}(V_{k\beta}c_{k\beta\sigma}^{\dag}d_{\ sigma}+Hc)+H_{\text{MBSs}}, \end{array} $$ (1)

waarbij $c_{k\beta \sigma }^{\dag } (c_{k\beta \sigma })$ een elektron met momentum creëert (vernietigt) k , energie ε _{k β} (de afhankelijkheid van spin wordt verwaarloosd voor normale metalen elektrode), en spin σ =↑ ,↓ in elektrode β =L ,R . Voor de QD is $d_{\sigma }^{\dag } (d_{\sigma })$ de creatie (annihilatie) operator van een elektron met een afstembaar energieniveau van de poortspanning ε _d , spin- σ , en intradot Coulomb-interactie U . De koppelsterkte tussen de QD en de leads wordt beschreven door V _{k β} . De laatste term H _MBS'en in verg. (1) staat voor de nul-energie MBS's aan tegenovergestelde uiteinden van de halfgeleidende nanodraad en hun koppeling met de QD [18]:

$$\begin{array}{@{}rcl@{}} {}H_{\text{MBSs}}=i\delta_{M}\eta_{1}\eta_{2}+\lambda_{1}( d_{\uparrow}-d_{\uparrow}^{\dag})\eta_{1}+i\lambda_{2}(d_{\uparrow}+d_{\uparrow}^{\dag})\eta_{ 2}, \end{array} $$ (2)

waarin δ _M is de overlapamplitude tussen de twee MBS's waarbij de operator voldoet aan zowel $\eta _{j}=\eta _{j}^{\dag } (j=1,2)$ als {η _ik ,η _j }=δ _{ik ,j} . De hopping-amplitude tussen MBS's en spin- ↑ elektronen in de QD wordt verklaard door λ _j . Het is handig om η . te schrijven _j in termen van de reguliere fermionische operatoren f als [18] $\eta _{1}=(f^{\dag }+f)/\sqrt {2}$ en $\eta _{2}=i(f^{\dag }- f)/\sqrt {2}$, en dan H _MBS'en wordt herschreven als:

$$\begin{array}{*{20}l} H_{\text{MBSs}}&=\delta_{M}\left(f^{\dag} f-\frac{1}{2}\right )+\frac{\lambda_{1}}{\sqrt{2}}\left(d_{\uparrow}-d_{\uparrow}^{\dag}\right)\left(f^{\dag} + f\right)\\&-\frac{\lambda_{2}}{\sqrt{2}}(d_{\uparrow}+d_{\uparrow}^{\dag})\left(f^{\dag }-f\rechts). \end{array} $$ (3)

We beschouwen het systeem in een lineair responsregime, d.w.z. onder een oneindig kleine voorspanning Δ V en temperatuurverschil Δ T tussen de linker- en rechterdraden worden de elektrische en warmtestromen van elke spincomponent verkregen als:

$$\begin{array}{*{20}l} &I_{e,\sigma}=-e^{2}L_{0,\sigma}\Delta V+\frac{e}{T}L_{1, \sigma}\Delta T, \end{array} $$ (4) $$\begin{array}{*{20}l} &I_{h,\sigma}=eI_{1,\sigma}\Delta V- \frac{1}{T}L_{2,\sigma}\Delta T, \end{array} $$ (5)

waar e is de elektronenlading en T de systeemevenwichtstemperatuur, en

$$\begin{array}{@{}rcl@{}} L_{n,\sigma}=\frac{1}{\hbar}\int (\varepsilon-\mu)^{n}\left[- \frac{\partial f(\varepsilon,\mu)}{\partial \varepsilon}\right]T_{\sigma}(\varepsilon)\frac{d\varepsilon}{2\pi}, \end{array} $$ (6)

waarbij $\hbar $ de gereduceerde constante van Planck is. We stellen het chemische potentieel van de leads in μ =0 als het energienulpunt. De Fermi-verdelingsfunctie wordt gegeven door f (ε ,μ )=1/{1+exp[(ε −μ )/k _B T ]} met k _B zijnde de Boltzmann-constante. De transmissiecoëfficiënt T _σ (ε ) wordt berekend met behulp van de functie van de vertraagde Groen als:

$$\begin{array}{@{}rcl@{}} T_{\sigma}(\varepsilon)=\frac{\Gamma_{L}\Gamma_{R}}{\Gamma_{L}+\Gamma_{ R}} [-2\text{Im}G_{\sigma}^{r}(\varepsilon)], \end{array} $$ (7)

waarbij $\Gamma _{L(R)}=2\pi \sum _{k}|V_{kL(R)}|^{2}\delta [\varepsilon -\varepsilon _{kL(R)} ]$ is de functie voor lijnbreedte. We passen de standaard bewegingsvergelijkingstechniek toe om de functie van Green te verkrijgen. De functies van de hogere orde Green worden afgekapt door schema 2 te volgen in ref. [39], d.w.z. negeer de gelijktijdige tunneling van het elektron met tegengestelde spin. Na wat eenvoudige berekeningen wordt de spin-up vertraagde functie van Green gegeven door:

$$ {\begin{aligned} G_{\uparrow}^{r}(\varepsilon)=\frac{\varepsilon_{-}-\Sigma^{M}_{1}-U\left\{1-\left[1-(\lambda_{1}^{2}-\lambda_{2}^{2})^{2}\tilde{B}\tilde{B}_{U} \right]\right\}}{\left(\varepsilon_{-}-\Sigma^{M}_{0}\right)\left(\varepsilon_{-}-U-\Sigma^{M}_{ 1}\right)}, \end{uitgelijnd}} $$ (8)

waar de MBS-geïnduceerde zelf-energieën

$$ \Sigma^{M}_{0}=B_{1}+\left(\lambda_{1}^{2}-\lambda_{2}^{2}\right)^{2}B\tilde {B}, $$ (9)

$$ \Sigma^{M}_{1}=B_{1}+\left(\lambda_{1}^{2}-\lambda_{2}^{2}\right)^{2}B\tilde {B}_{U}, $$ (10)

met

$$\begin{array}{*{20}l} &B=\frac{\varepsilon}{\varepsilon^{2}-\delta_{M}^{2}}, \end{array} $$ (11 ) $$\begin{array}{*{20}l} &B_{1}=\frac{1}{2}\left(\frac{\lambda_{1}^{2}-\lambda_{2}^ {2}}{\varepsilon-\delta_{M}}+\frac{\lambda_{1}^{2}+\lambda_{2}^{2}}{\varepsilon+\delta_{M}}\right) , \end{array} $$ (12) $$\begin{array}{*{20}l} &\tilde{B}=\frac{B}{\varepsilon_{+}+B_{2}}, \end{array} $$ (13) $$\begin{array}{*{20}l} &\tilde{B}_{U}=\frac{B}{\varepsilon_{+}+U-B_ {2}}, \end{array} $$ (14)

waarin

$$ B_{2}=\frac{1}{2}\left(\frac{\lambda_{1}^{2}-\lambda_{2}^{2}}{\varepsilon+\delta_{M}} +\frac{\lambda_{1}^{2}+\lambda_{2}^{2}}{\varepsilon-\delta_{M}}\right), $$ (15)

en ε _± =ε ±ε _d +ik (Γ _L +Γ _R )/2. Bij afwezigheid van dot-MBSs-hybridisatie (λ ₁ =λ ₂ =0), hebben we $\Sigma ^{M}_{0,1}=0$ en $G_{\uparrow }^{r}(\varepsilon)$ herstelt die van ref. [39]. Het is ook de functie van de spin-down vertraagde Groen door n . te veranderen _↓ in n _↑ . Het bezettingsnummer wordt zelfconsistent berekend uit:

$$\begin{array}{@{}rcl@{}} n_{\sigma}=\int \frac{d\varepsilon}{2\pi}\frac{\Gamma_{L}f_{L}(\ varepsilon)+\Gamma_{R}f_{R}(\varepsilon)}{\Gamma_{L}+\Gamma_{R}}[-2\text{Im}G_{\sigma}^{r}(\varepsilon )], \end{array} $$ (16)

waar f _{L /R} (ε ) is de Fermi-verdelingsfunctie in de linker/rechter elektrode.

Zodra de transmissiefunctie is verkregen uit de functie van Green, worden de elektrische geleiding en het thermovermogen (Seebeck-coëfficiënt) van elke spincomponent gegeven door G _σ =e ² L _0,σ en S _σ =−L _1,σ /(e T L _0,σ ), respectievelijk.

Resultaten en discussies

In wat volgt gaan we uit van een symmetrische koppeling tussen de QD en de elektroden, en stellen we Γ =2Γ _L =2Γ _R =1 als de energie-eenheid. De intradot Coulomb-interactie is vastgesteld als U =10Γ . We bestuderen eerst het geval van de QD die is gekoppeld aan alleen MBS-1 met verschillende hybridisatiesterktes λ ₁ in Fig. 2 door λ . in te stellen ₂ =0. Voor λ ₁ =0, ontwikkelt de conductantie van elke spincomponent in Fig. 2a twee pieken die zich respectievelijk op ε bevinden _d =−μ en −μ −U . Merk op dat de QD nu vrij is van spinpolarisatie veroorzaakt door de MBS, en de conductantie van de twee spincomponenten is gelijk aan elkaar (G _↑ =G _↓ ), overeenkomstig. De hybridisatie tussen de MBS en de QD inschakelen (λ ₁ ≠0), de grootte van G _↑ wordt monotoon onderdrukt zoals weergegeven in figuur 2a, wat consistent is met eerdere resultaten [18, 34, 35]. De waarde van G _↓ , is echter bijna ongewijzigd, zelfs het bezettingsnummer n _↓ wordt gewijzigd door λ ₁ vanwege de aanwezigheid van intradot Coulomb-interactie (die niet in de afbeelding wordt getoond). Ondertussen zijn de positie en breedte van de pieken in G _↑ worden enigszins gewijzigd door de waarde van λ ₁ vanwege de niveau-renormalisatie door de dot-Majorana-koppeling [18, 34, 35]. De configuratie van de totale conductantie G =G _↑ +G _↓ in Fig. 2c lijkt op die van G _↑ .

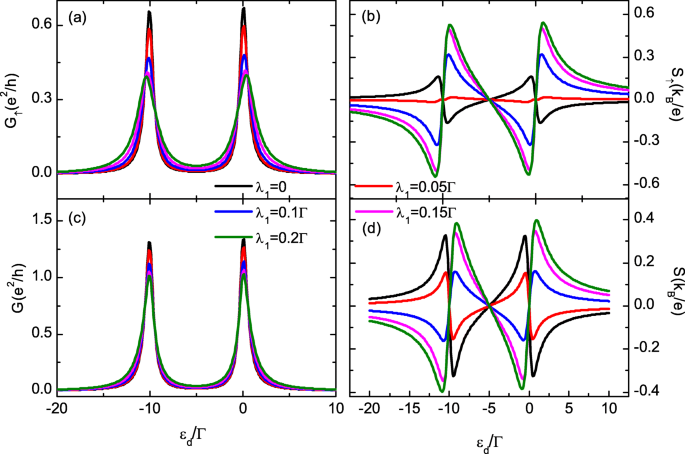
Spin-afhankelijke conductantie en thermopower voor verschillende dot-Majorana koppelingssterktes (kleur online). De spin-up en totale geleiding in a , c en thermokracht in b , d vers punt-niveau. De spin-down conductantie en thermopower zijn vrijwel onveranderd door de dot-Majorana koppelingssterkte λ ₁ , en ze overlappen met de zwarte ononderbroken lijnen in a en c , respectievelijk. Andere parameters zijn temperatuur T =0.025Γ ,Δ _M =0,U =10Γ , en λ ₂ =0

De thermokracht S _↑ in Fig. 2b toont de typische zaagtandconfiguratie en heeft drie nulpunten afzonderlijk op ε _d =μ ,−U /2, en μ −U [41, 42]. Het ontwikkelt een paar scherpe pieken met tegengestelde tekens in elk van de twee resonantietoestanden (ε _d =μ ,μ −U ) en verandert van teken wanneer ε _d passeert elk nulpunt. Bij afwezigheid van dot-MBSs-hybridisatie (λ ₁ =0) zoals aangegeven door de ononderbroken zwarte lijn in Fig. 2b, S _↑ is positief (negatief) wanneer ε _d ligt onder (boven) het nulpunt, aangezien de belangrijkste dragers elektronen (gaten) zijn. Met toenemende λ ₁ , de spin-down thermopower S _↓ is ongewijzigd en de absolute waarde van S _↑ wordt eerst onderdrukt en vervolgens versterkt. Voor voldoende grote λ ₁ ,S _↑ verandert zijn teken zoals weergegeven in Fig. 2b. Met verder verhoogde λ ₁ , de absolute waarde van S _↑ groter is dan die van S _↓ en de totale thermokracht S =S _↑ +S _↓ verandert ook zijn teken. Een dergelijk fenomeen is ook eerder gevonden in het spinloze model [35-37]. In feite werd de tekenverandering van de thermokracht in QD-gebaseerd apparaat zonder MBS's toegeschreven aan verschillende oorzaken, zoals de systeemevenwichtstemperatuur [29], magnetisch momentum van de elektroden [43], Coulomb-interactie [43, 44], koppeling sterkte tussen de QD's, het aangelegde magnetische veld, het kwantuminterferentie-effect of de magnetische flux die door meerdere stippen dringt [45, 46]. De bovenstaande mechanismen verschillen behoorlijk van het huidige geval, en de tekenverandering van de thermokracht door de hybridisatie tussen de QD en de MBS's te veranderen is nuttig voor het detecteren van de MBS's [35-37].

Figuur 3a, b toont de totale conductantie G en themopower S variërend met het puntniveau ε _d voor verschillende waarden van de temperatuur T . De piekwaarde van G wordt eerst versterkt en vervolgens onderdrukt door de temperatuur te verhogen, zoals weergegeven in figuur 3a. De grootte van de thermokracht in figuur 3b wordt echter voornamelijk versterkt door de temperatuur te verhogen, omdat er meer elektronen (gaten) worden geëxciteerd boven (onder) de chemische potentiaal. Bovendien, S verandert zijn teken voor de gevallen van T =0, 1 en 0, 2 zoals aangegeven door de roze en groene lijnen in figuur 3b, wat vergelijkbaar is met het geval van thermo-elektrisch effect in op QD gebaseerde structuur zonder MBS's. Voor T =0.2Γ , de piekwaarde van S kan oplopen tot 2k _B /e , wat één orde groter is dan die van T =0,001. In feite hebben we gecontroleerd of de omvang van de thermokracht verder kan worden vergroot door de temperatuur te verhogen. In dit artikel concentreren we ons echter op de tekenverandering van S bij relatief lage temperatuur, wat meestal het geval is bij de MBS's die in experimenten zijn gevormd. Figuur 3c, d geeft de conductantie en het thermovermogen weer voor verschillende waarden van directe hybridisatie van de twee MBS's aan tegenovergestelde uiteinden van de nanodraad op vaste T =0.025Γ . De piekwaarde van de conductantie in Fig. 3c wordt monotoon verhoogd door het verhogen van δ _M , wat in overeenstemming is met de resultaten gevonden door López et al. [35]. De thermokracht in Fig. 3d verandert zijn teken voor 0,03Γ <δ _M <0.05Γ , die groter is dan de temperatuur T =0.025Γ . In ref. [32], ontdekten ze dat de thermokracht van teken verandert rond δ _M ≈k _B T in het spinloze model. In het huidige artikel verandert het teken van S komt voor bij relatief grotere δ _M omdat de MBS's zijn gekoppeld aan slechts één elektronen in de spinrichting. Bovendien kan de piekwaarde van de thermokracht ook worden verbeterd door δ . te verhogen _M .

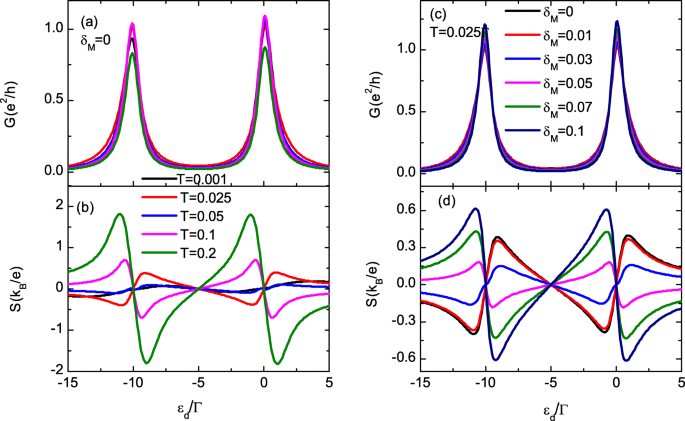
Geleiding en thermopower (kleur online). Tellergrafiek van totale geleiding G en thermopower S als functies van ε _d en Δ _M in een , b , temperatuur T in c , d , respectievelijk. De waarde van λ ₁ is vastgesteld op 0.2Γ . De temperatuur in a , c is 0,025Γ , en in c , d Δ _M =0. Andere parameters zijn dezelfde als die van Fig. 2

We laten de spin-opgeloste thermokrachten afzonderlijk zien als functies van λ ₁ en δ _M in Fig. 4. De spin-up thermopower S _↑ in Fig. 4a neemt eerst toe, bereikt een maximum en neemt vervolgens af met toenemende λ ₁ . Bij voldoende grote λ ₁ , het blijft op een stabiele waarde. De waarde van spin-down thermopower S _↓ is ongewijzigd door λ ₁ zoals verwacht. Het gedrag van S _↑ en S _↓ twee interessante resultaten opleveren:de ene is de 100% spin-gepolariseerde thermokracht wanneer S _↑ =0 maar S _↓ heeft een eindige waarde die kan worden gebruikt voor het filteren van elektronenspin; de andere is de eindige pure spin-thermokracht S _s =S _↑ −S _↓ met nullast thermopower S _c =S _↑ +S _↓ =0 die plaatsvond toen S _↑ =−S _↓ zoals weergegeven door de stippen in Fig. 4b. Bij een gesloten circuit zijn de 100% spin-gepolariseerde en pure spin-thermokrachten afzonderlijk de overeenkomstige stromen, die virtueel zijn in spintronische apparaten. Vergelijkbare resultaten worden gevonden in Fig. 4b, d, waarin S _↑ ondergaat tekenverandering door δ . te veranderen _M , terwijl S _↓ blijft onveranderd. We benadrukken dat de huidige 100% spin-gepolariseerde en pure spin-thermokrachten ontstaan in de afwezigheid van een magnetisch veld of magnetische materialen in de QD.

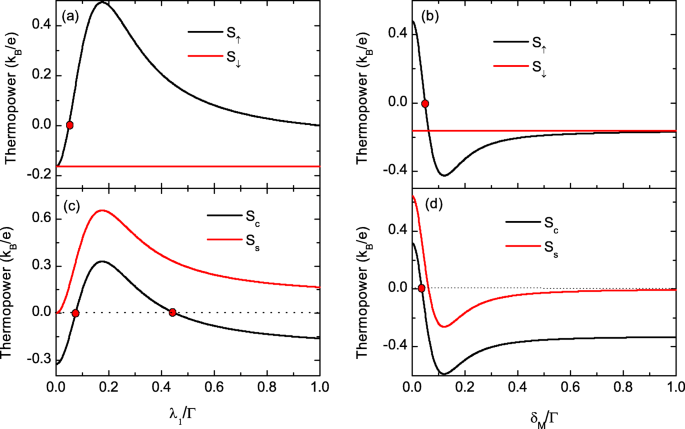
Thermopowers variërend met dot-Majorana koppelingssterkte en directe overlap. De thermokrachten als functies van λ ₁ in een , b met Δ _M =0, en Δ _M in c , d met λ ₁ =0.2Γ , respectievelijk. Andere parameters zijn dezelfde als die van Fig. 2

In Fig. 5 bestuderen we het geval van beide MBS's aan de tegenovergestelde uiteinden van de nanodraad die zijn gekoppeld aan de QD wanneer de draad en de stip voldoende dicht bij elkaar liggen met δ _M =0. Figuur 5a laat zien dat de totale conductantie G behoudt de dubbele-piekconfiguratie in aanwezigheid van λ ₂ . De hoogte van de pieken wordt onderdrukt door λ . te vergroten ₂ . De lijnvorm van S is ook ongewijzigd door de waarde van λ ₂ zoals aangegeven door Fig. 5b. De piekwaarde van S zal aanzienlijk worden verbeterd omdat het thermovermogen omgekeerd evenredig is met de geleiding. Voor λ ₂ ∼0.2Γ , de grootte van de thermokracht kan oplopen tot 2 k _B /e . Bovendien vinden we dat S zal het teken niet veranderen door de waarde van λ . aan te passen ₂ . Figuur 6 toont het totale thermovermogen als functie van ε _d voor verschillende waarden van directe hybridisatie tussen de MBS's δ _M door λ . te repareren ₁ =λ ₂ =0.2Γ . Het laat zien dat zowel de grootte als het teken effectief kunnen worden veranderd door δ . af te stemmen _M , wat vergelijkbaar is met het geval dat slechts één van de MBS'en aan de QD is gekoppeld. Ten slotte bespreken we kort de experimentele realisatie van de huidige apparaten. De nanodraad die de MBS's host, kan worden gefabriceerd met InAs gegroeid door moleculaire bundelepitaxie met enkele nanometers epitaxiale Al-laag [47]. Het is experimenteel bewezen dat een harde supergeleidende kloof kan worden geïnduceerd op een dergelijk soort nanodraden [47, 48] door een kritisch magnetisch veld van meer dan 2 T langs de draadas aan te leggen [20]. Een QD wordt gevormd in het kale InAs-segment aan het einde van de draad vanwege de dichtheid van toestandsgradiënten aan de randen van de Al-schaal [20, 47, 48].

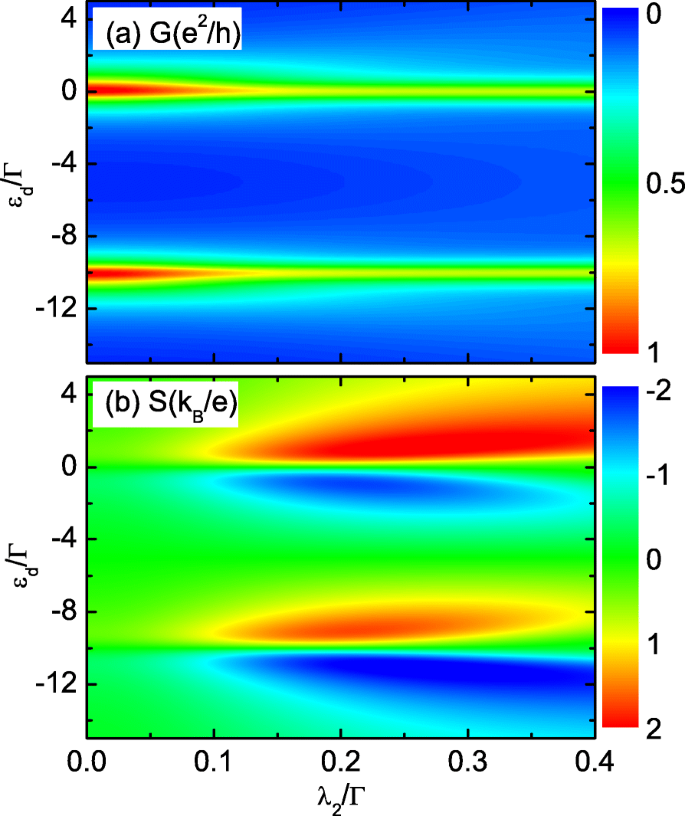
Invloeden van de andere dot-Majorana koppeling op de thermopower (kleur online). Gevolgen van λ ₂ op de totale geleiding (a ) en thermokracht (b ) met λ ₁ =0.2Γ ,δ _M =0. Andere parameters zijn dezelfde als die van Fig. 2

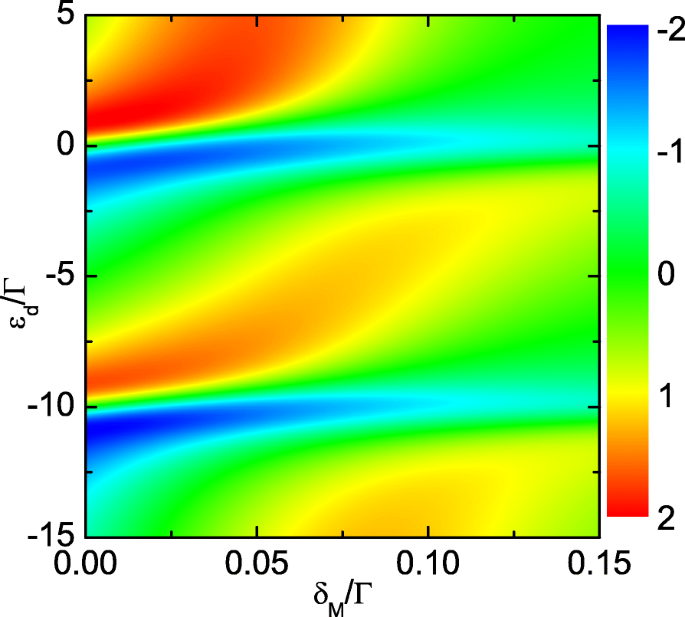
Tellerplot van de thermopower (kleur online). Tellergrafiek van de thermokracht als functie van ε _d en λ ₂ voor λ ₁ =0.2Γ . Andere parameters zijn dezelfde als die van Fig. 2

Conclusies

Concluderend hebben we de eigenschappen van de elektrische geleiding en thermokracht bestudeerd in een kwantumdot verbonden met de linker en rechter normale metalen elektroden met Coulomb-interactie. De stip is ook gekoppeld aan MBS's gevormd in een halfgeleidende nanodraad. We vinden dat de MBS's de geleiding en het thermovermogen van de spincomponent beïnvloeden waaraan het alleen koppelt, hoewel de spin-up en spin-down elektronen met elkaar interageren via de Coulomb-afstoting. Het teken van de thermopower kan worden veranderd door de dot-MBSs-hybridisatiesterkte, de richtingshybridisatie tussen de MBS's en de systeemtemperatuur aan te passen. Grote waarde van ofwel 100% spin-gepolariseerde of pure spin-kracht kan worden verkregen in een niet-magnetische QD-structuur. De koppeling tussen de stip en beide twee MBS's kan alleen de grootte van de thermokracht veranderen, maar niet het teken ervan. Onze resultaten kunnen nuttig zijn bij het detecteren van het bestaan van de MBS's via thermo-elektrische techniek.

Beschikbaarheid van gegevens en materialen

De datasets die de conclusies van dit artikel ondersteunen, zijn in het artikel opgenomen.

Afkortingen

QD:: Kwantumpunt
MBS'en:: Majorana gebonden staten

Beheersing van DNA-translocatie via vaste-stof nanoporiën 2D/2D heterojunctie van R-schema Ti3C2 MXene/MoS2 Nanosheets voor verbeterde fotokatalytische prestaties

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal