Hoogwaardige dual-band Fano-resonanties geïnduceerd door dubbel gebonden toestanden in het continuüm met behulp van een vlakke nanogatplaat

Methoden

Latticestructuur en ontwerp

Figuur 1 toont de schematische geometrie van de voorgestelde PNS en de transmissiespectra. De PNS bestaat uit vier nanogaten die kunnen worden verkleind (Δ < 0) of vergroot (Δ > 0) met een verschuivingsafstand van Δ langs de diagonalen van het superrooster, en Δ = 0 komt overeen met een eenvoudig rooster met een halveringstijd, waarbij elk nanogat bevindt zich in het midden van een kwart van het superrooster. De periode en de hoogte van de PNS zijn respectievelijk Λ en H; de straal van het nanogat is r . De brekingsindex van het PNS is n _s = 3.2, en de achtergrond is lucht met de brekingsindex van n _een = 1 Figuur 1c toont de spectra van het PNS als functie van de verschuivingsafstand van Δ, waarbij het PNS wordt verlicht door een normaal invallende x -gepolariseerd licht. De spectra en de elektromagnetische veldverdelingen van de PNS die in dit artikel worden gepresenteerd, worden berekend met behulp van de commerciële software van de eindige-elementenmethode van COMSOL Multiphysics. Zoals getoond in figuur 1c, is er geen Fano-resonantie voor de niet-gekrompen PNS met Δ = 0. Er kunnen echter twee Fano-resonanties met 100% modulatiediepten (gedefinieerd als de transmissieverschillen tussen Fano-pieken en Fano-dips) worden verkregen door de nanogaten lichtjes krimpen of uitzetten. In vergelijking met de transmissierespons van de niet-gekrompen PNS, varieert de transmissierespons van de gekrompen PNS abrupt, terwijl de zijbanden bijna hetzelfde blijven.

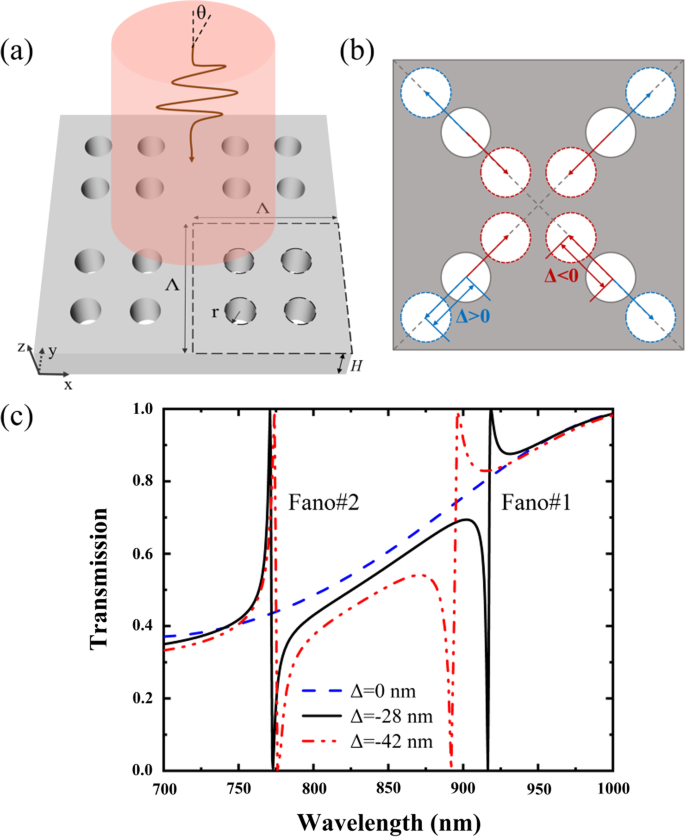
een Perspectief van de PNS. b Verticale weergave van het PNS als vier nanogaten die krimpen (Δ < 0) of uitzetten (Δ > 0) langs de diagonalen van het superrooster. c Transmissiespectra van het PNS als functie van de verschuivingsafstand van Δ. De PNS staat onder de verlichting van de x -gepolariseerde invallende golf met de invalshoek θ = 0. De parameters van de PNS zijn:Λ = 350 nm, r = 35 nm en H = 175 nm

Om de evolutie van de dual-band Fano-resonanties die voortkomen uit het krimpen of uitzetten van de tetramerized gaten duidelijk te laten zien, wordt de transmissie 2D-kaart van de PNS als functie van de verschuivingsafstand van Δ getoond in figuur 2a. Zoals getoond in Fig. 2a, zijn er twee BIC's opgetreden in het golflengtegebied van belang als Δ  =0, en een vergelijkbaar fenomeen van dubbele BIC's werd eerder gerapporteerd in de structuren van dual-grating metamembranen [13] en gesplitste ringresonator [21]. In het geval van Δ ≠ 0 worden dual-band Fano-resonanties gerealiseerd omdat BIC's worden geïnduceerd tot QBIC's vanwege de symmetriebreking van de PNS, dwz van de centrosymmetrie van een eenvoudig rooster naar de viervoudige rotatie (C₄ ) symmetrie van superrooster. Bovendien, omdat de C₄ symmetrie van de PNS kan worden gehandhaafd als de tetramerized gaten worden gekrompen of uitgebreid langs de diagonalen van het superrooster, de transmissiespectra van de PNS zijn hetzelfde voor dezelfde absolute waarde van |Δ|. In principe verkleint het krimpen of uitzetten van de tetrameriseerde gaten het gebied van de eerste Brillouin-zone van het PNS, aangezien de eenheidscel van het PNS verandert van eenvoudig rooster in superrooster, en symmetrie-beschermde BIC kan worden geëxciteerd bij normale incidentie vanwege de introductie van oppervlakteverstoring en Brillouin-zonevouwing van de PNS [42, 43]. Over het algemeen vertoont de Q-factor van een symmetrie-beschermde BIC een inverse kwadratische afhankelijkheid van de mate van asymmetrie δ gebaseerd op de storingstheorie [21]:

waar ĸ is een evenredigheidsconstante, S is de oppervlakte van een superrooster, ω is de hoekfrequentie en de asymmetrieparameter is \(\delta { =}\sqrt 2 \Delta /\Lambda\).

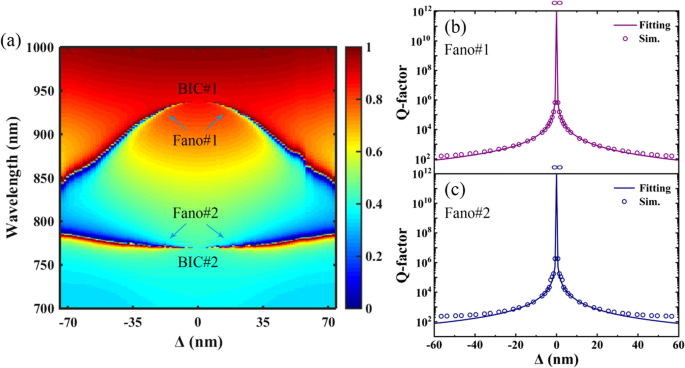
een Transmissie 2D-kaart van het PNS als functie van de verschuivingsafstand van Δ langs de diagonalen van het superrooster. b en c Q-factor en het passende resultaat van respectievelijk Fano#1 en Fano#2. Andere parameters zijn hetzelfde als in Afb. 1c

Figuur 2b, c toont de Q-factor en het aanpasresultaat van respectievelijk Fano#1 en Fano#2. De Q-factor van het PNS wordt berekend als een verhouding tussen de resonantiegolflengte λ _r en de volledige breedte bij half maximum (FWHM) Δλ, waarbij Δλ het golflengtegebied is tussen de piek en dip van Fano-resonantie. De aanpasresultaten van de PNS worden berekend met behulp van Vgl. (1). Zoals getoond in Fig. 2b, c, worden divergerende trajecten van de PNS waar de Q-factoren divergeren tot oneindig bij Δ = 0 gevalideerd door de inverse kwadratenrelatie te gebruiken om in de gegevens te passen. Er kunnen uitstekende aanpasresultaten worden verkregen en de lichte onenigheid bij grotere asymmetrie is te wijten aan de afwijking van de aanname van een kleine verstoring in Vgl. (1). Het grote voordeel van de PNS is dat de locatie en de Q-factor van de dual-band Fano-resonanties kunnen worden aangepast door de tetramerized gaten te verkleinen of uit te breiden, wat de dynamische controle van de resonantieprestaties van de high-Q-factor multiple vergemakkelijkt. Fano-resonanties.

Fysieke mechanismen en interpretatie

Om inzicht te krijgen in de oorsprong van de dual-band Fano-resonanties via het verkleinen of vergroten van de tetrameriseerde gaten van de PNS, ontleden we de verre-veldstraling van BIC- en Fano-resonantie in bijdragen van verschillende meerpolige componenten om hun kenmerken verder te bespreken. De multipoolmomenten kunnen worden berekend op basis van de verplaatsingsstroomdichtheid j in het superrooster van de PNS [26, 44, 45]:

waar P , M , T , V ^{(e )} en Q ^{(m )} zijn respectievelijk de momenten van elektrische dipool (ED), magnetische dipool (MD), toroidale dipool (TD), elektrische quadrupool (EQ) en magnetische quadrupool (MQ); c is de lichtsnelheid in vacuüm, en α , β = x , j , z . Hier de ladingsdichtheid ρ , die gewoonlijk voorkomt in de definitie van ED en MQ, is vervangen door verplaatsingsstroomdichtheid j via lading behoud relatie van \(i\omega \rho + \nabla \cdot {\varvec{j}} =0\). In het geval van harmonische excitatie ~ exp(iωt ), kan het verstrooiingsvermogen van de geïnduceerde multipoolmomenten die bijdragen aan de verre-veldrespons worden geschreven als:

waarbij de eerste twee termen overeenkomen met de conventionele ED (lading) en MD-verstrooiing. De derde term komt overeen met de TD-verstrooiing. De vierde en vijfde termen komen van EQ en MQ. De laatste term is de term van hogere orde die de multipoolverstrooiing van hoge orde en koppeling daartussen bevat en die over het algemeen kan worden genegeerd. Door gebruik te maken van vergelijkingen. (2)–(7), de bijdragen van verschillende multipolen aan de verstrooiingskracht van het verre veld kunnen worden verkregen.

Figuur 3 toont het verstrooiingsvermogen van verschillende multipolen van de PNS voor verschillende verschuivingsafstanden van Δ, andere parameters zijn hetzelfde als in figuur 1c. Zoals getoond in Fig. 3a-d, zijn ED en MD voor de PNS met Δ = 0 de dominerende dipolen en ze resoneren niet in het golflengtegebied van belang. Door echter de nanogaten van de PNS te verkleinen of uit te breiden met |Δ|≠ 0, kunnen dual-band Fano-resonanties worden gerealiseerd vanwege de excitaties van de resonante dipoolmodi. Om de belangrijke rollen van de resonante dipoolmodi bij het vormen van de waargenomen dual-band Fano-resonanties duidelijk te zien, toont Fig. 3e, f het genormaliseerde verstrooiingsvermogen van verschillende multipolen met Δ =  − 28 nm rond respectievelijk Fano#1 en Fano#2 . Zoals weergegeven in figuur 3e, zijn de dominante resonantiemodi ED en TD rond Fano # 1 en Fano # 1 is het directe gevolg van de resonante koppeling van de elektrische toroïdale dipolen. In het bijzonder zijn ED en TD sterk verbeterd tot een vergelijkbare grootte aan de resonantiepunt (918,5 nm) van Fano # 1; dus 100% transmissie kan worden verkregen vanwege de destructieve interferentie tussen ED en TD. Terwijl voor de resonantiedip (916,5 nm) van Fano#1 de reflectie wordt gemaximaliseerd en de transmissie naar nul gaat vanwege de verbeterde verstrooiing van ED en TD. Evenzo, zoals weergegeven in figuur 3f, komt Fano #2 voort uit de resonante koppeling van de magnetische toroïdale dipolen, de punt (771,1 nm) geeft de destructieve interferentie tussen MD en TD aan, terwijl de dip (772,9 nm) wordt geassocieerd met de verbeterde verstrooiing van MD en TD. Let op:vanwege de sterke koppeling van elektrische ringkerndipolen of magnetische ringkerndipolen zijn de resonantiemodi robuust voor zowel Fano#1 als Fano#2, zelfs als Δ wordt gevarieerd.

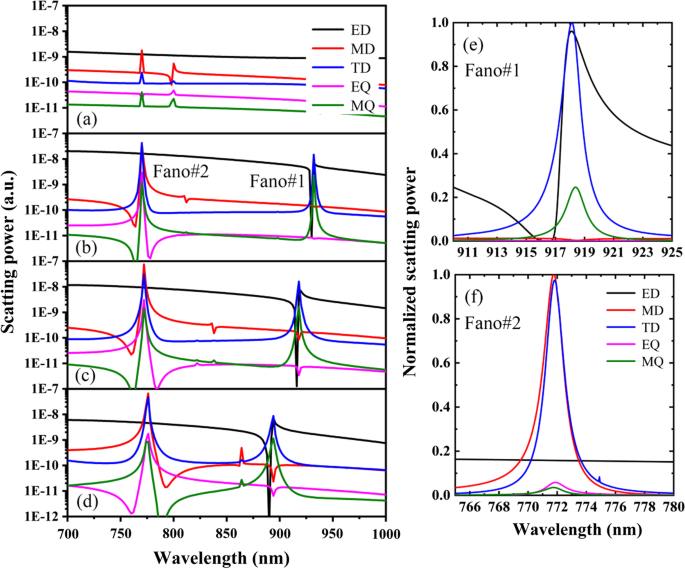
Verstrooiingskracht van de Cartesiaanse ED, MD, TD, EQ en MQ wanneer a Δ = 0, b Δ =  − 14 nm, c Δ =  − 28 nm en d Δ =  − 42 nm. e en f Genormaliseerd verstrooiingsvermogen van verschillende multipolen met respectievelijk Δ =  − 28 nm rond Fano#1 en Fano#2. Andere parameters zijn hetzelfde als in Afb. 1c

Om de transmissierespons van dual-band Fano-resonanties in het verre veld te koppelen aan de excitaties van geïnduceerde multipoolmomenten, worden de distributies van elektromagnetisch veld en verplaatsingsstroom van Fano-resonanties van het superrooster van de PNS getoond in figuur 4. Zoals getoond in Fig. 4a, b, het elektrische veld van Fano#1 is goed opgesloten in het superrooster van de PNS met de verplaatsingsstroom langs de x as, wat een ED-resonantiemodus aangeeft. Bovendien vormt de verplaatsingsstroom van Fano#1 twee omgekeerde lussen tussen het midden en de randen van het superrooster, en vormt het magnetische veld een lus in de yz vlak, overeenkomend met een TD-resonantiemodus langs de x as [44, 46]. Daarom is Fano#1 ontstaan ​​uit de resonante koppeling tussen de ED- en TD-modi, die in lijn zijn met de voorspelde resultaten van de multipooldecomposities zoals hierboven vermeld. Vanwege de resonantiekenmerken van de elektrische toroïdale dipolen van Fano # 1, de distributies van elektromagnetisch veld en verplaatsingsstroom bij de resonantiepiek (918,5 nm), centrale golflengte (917,5 nm) en resonantiedip (916,5 nm) van Fano #1 zijn bijna hetzelfde, behalve een klein verschil in de veldamplitude (Extra bestand 1:Fig. S1). In het geval van Fano # 2, zoals weergegeven in figuur 4c, is het elektrische veld sterk verbeterd en vormt de verplaatsingsstroom twee omgekeerde lussen tussen het midden van het superrooster en het aangrenzende superrooster van de PNS, wat wijst op een TD-resonantiemodus langs de z as. Bovendien is het magnetische veld van Fano#2 sterk gelokaliseerd in het superrooster met de richting langs de y as, zoals weergegeven in figuur 4d, met een MD-resonantiemodus. Als resultaat is Fano#2 het directe gevolg van de resonante koppeling van de magnetische toroïdale dipolen, wat in overeenstemming is met de voorspelling van de multipooldecomposities van het verre veld van het PNS. Door de koppeling van de magnetische toroïdale dipolen van Fano #2 vertonen het elektromagnetische veld en de verplaatsingsstroom bij de resonantiepiek (771,1 nm), de centrale golflengte (772,0 nm) en de resonantiedaling (722,9 nm) van Fano #2 vergelijkbare distributies (Extra bestand 1:Afbeelding S2).

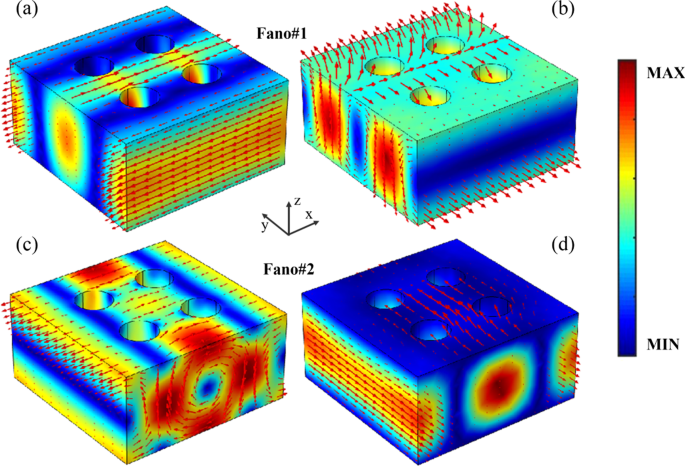
Distributies van elektromagnetisch veld en verplaatsingsstroom van Fano-resonanties van het superrooster van de PNS, de kleurenbalk vertegenwoordigt de veldamplitude en de rode pijlen geven de veldvector of verplaatsingsstroomvector aan. Andere parameters zijn hetzelfde als in figuur 1c met Δ =  − 28 nm. een en c Verdelingen van elektrische veldamplitude en verplaatsingsstroomvector van respectievelijk Fano#1 en Fano#2. b en d Verdelingen van magnetische veldamplitude en magnetische veldvector van respectievelijk Fano#1 en Fano#2

Resultaten en discussie

Afbeelding 5 toont transmissiespectra van het PNS als functie van de straal r van het nanogat en andere parameters zijn hetzelfde als in figuur 1c met Δ =  − 28 nm. Zoals weergegeven in figuur 5a, kunnen dual-band Fano-resonanties worden gehandhaafd als r varieert van 0 tot de maximale waarde van 67,5 nm, d.w.z. , de tetrameriseerde gaten raken elkaar in het superrooster. De toename van de straal van het nanogat r verhoogt de oppervlakteverstoringen van het PNS en vermindert ook de effectieve brekingsindex (ERI), wat resulteert in de verhoogde Q-factor en de blauwverschuiving van de Fano-resonanties. In het bijzonder is de resonantielocatie van Fano#1 gevoeliger voor de variatie van r , en de dual-band Fano-resonanties hebben de neiging om samen te smelten tot één resonantiemodus wanneer de tetrameriseerde gaten elkaar naderen. Zoals weergegeven in figuur 5b, is de toename van r verschuift niet alleen de resonantielocatie van de Fano-resonanties blauw, maar verhoogt ook hun FWHM's. Als r wordt verhoogd van 25 naar 45 nm, worden de resonantiepieken van Fano#1 en Fano#2 blauwverschoven van respectievelijk 936,7 nm en 793,2 nm tot 887,6 nm en 743,8 nm; en hun FWHM's worden verhoogd van respectievelijk 0,8 nm en 0,6 nm tot 6,8 nm en 3,1 nm. Let op de toename van r verbetert ook de modulatiediepten van de Fano-resonanties, en 100% modulatiediepten kunnen worden gerealiseerd als r groter is dan 30 nm. Door de verschuiving van de Fano-piekgolflengte die wordt beïnvloed door de structurele parameters van de PNS te evalueren, wordt bovendien aangetoond dat de straal van het nanogat r is de meest gevoelige structurele parameters voor zowel Fano#1 als Fano#2 (Extra bestand 1:Figuur S3). Daarom is de variatie van r biedt een effectieve benadering om de resonantieprestaties van de dual-band Fano-resonanties van de PNS dynamisch te regelen.

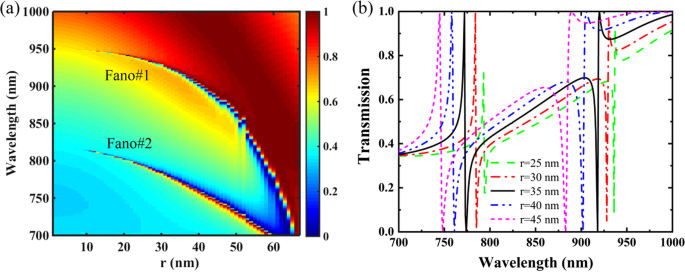
een Transmissie 2D-kaart van het PNS als functie van de straal r van het nanogat. b Transmissiespectra van de PNS voor verschillende nanogatradius r . Andere parameters zijn hetzelfde als in Afb. 1c met Δ =  − 28 nm

Afbeelding 6 toont de invloeden van de symmetrie van de structuur op de transmissiereacties van het PNS, waarbij de straal r' van twee nanogaten wordt gevarieerd van nul tot raaklijn aan elkaar, en andere parameters zijn hetzelfde als in figuur 1c met Δ =  − 28 nm. Zoals weergegeven in figuur 6a, voor het superrooster met spiegelsymmetrie langs de x as (richting van elektrisch veld van invallend licht), als de straal r ′ van de twee nanogaten wordt vergroot, de resonantielocaties van de dual-band Fano-resonanties zijn blauwverschoven vanwege de afname van de ERI van de PNS, en hun bandbreedtes worden breder vanwege de toegenomen oppervlakteverstoringen. Echter, zoals getoond in Fig. 6b, hoewel de twee Fano-resonanties kunnen worden gehandhaafd met de toename van r ′, zullen twee extra Fano-resonanties optreden als de spiegelsymmetrie van het superrooster langs de x as is gebroken. In het algemeen, het breken van de structurele symmetrie langs de x (j ) as zal ook de symmetrie van de modus langs de x . verbreken (j ) as van een periodiek rooster, en de niet-stralende niet-gedegenereerde modus kan koppelen aan buitenstraling vanwege zijn gedegenereerde component [47]. Daarom is het feit dat de twee extra Fano-resonanties alleen aanwezig zijn voor de door spiegelsymmetrie gebroken structuur langs x as geeft aan dat ze te wijten zijn aan de verstoorde niet-gedegenereerde modi.

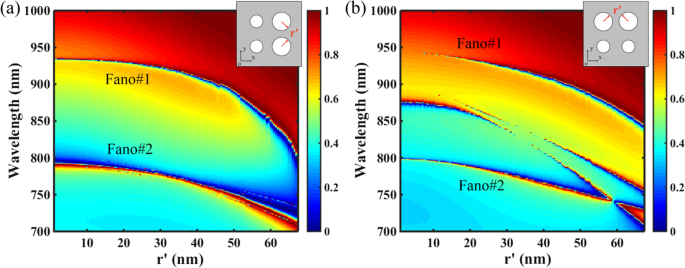
Invloeden van de symmetrie van de structuur op transmissiereacties van het PNS. Andere parameters zijn hetzelfde als in figuur 1c met Δ =  − 28 nm. De ingevoegde figuren geven het schematische diagram van het superrooster van de PNS aan. een Transmissie 2D-kaart van het PNS als functie van de straal r ′ van twee nanogaten, waarbij de structurele symmetrie van het superrooster langs de x as blijft behouden. b Transmissie 2D-kaart van het PNS als functie van de straal r ′ van twee nanogaten, waarbij de structurele symmetrie van het superrooster langs de x as is kapot

We hebben verder de resonantieprestaties van de PNS gekarakteriseerd onder de invloeden van de invalshoek en polarisatiehoek. Zoals weergegeven in figuur 7a, zijn dual-band Fano-resonanties van de PNS immuun voor de variatie van de polarisatiehoek als gevolg van de C₄ symmetrische topologie. Als de polarisatiehoek wordt gewijzigd van 0 naar 90°, dat wil zeggen van x -polarisatie naar y -polarisatie, Fano#1 en Fano#2 worden hetzelfde gehouden. In het geval van een invalshoek, zoals weergegeven in figuur 7b, hoewel Fano#1 ook ongevoelig is voor de variatie van de invalshoek, wordt Fano#2 roodverschoven als de invalshoek afwijkt van de normale inval, en een extra Fano-resonantie (Fano#3) is opgetreden omdat de onderdrukking van het stralingsverval van de symmetrie-beschermde BIC wordt geannuleerd bij een niet-normale inval. In het algemeen is dit type onderdrukking van het stralingsverval van BIC nauw verwant aan de destructieve interferentie tussen de uitgezonden stralingsvelden van twee zich in tegengestelde richting voortplantende lekkende modi aan een van de twee randen van de stopband van de periodieke roosters [48]. Let op:vanwege de sterke koppeling tussen Fano#2 en Fano#3 kan een smal geïnduceerd transparantievenster worden opgewekt in het nabijheidsgebied ertussen.

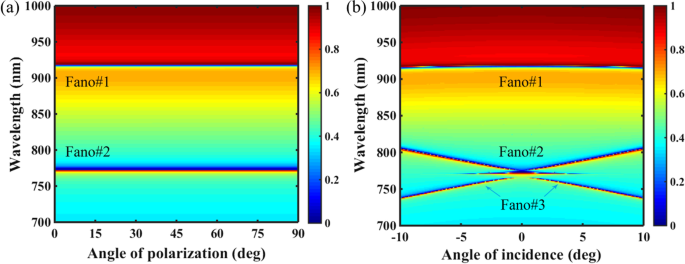
een Transmissie 2D-kaart van het PNS als functie van de polarisatiehoek. b Transmissie 2D-kaart van het PNS als functie van de invalshoek. Andere parameters zijn hetzelfde als in Afb. 1c met Δ =  − 28 nm

Ten slotte hebben we aangetoond dat meerdere Fano-resonanties kunnen worden verkregen door de plaathoogte H van de PNS te vergroten. Figuur 8 toont de transmissie 2D-kaart van de PNS als functies van H voor de niet-gekrompen (Δ = 0 nm) en gekrompen (Δ =  − 28 nm) structuren. Zoals getoond in Fig. 8a, is er geen Fano-resonantie behalve de Fabry-Pérot (F-P) resonanties voor de niet-gekrompen PNS als H wordt gevarieerd. Volgens de F-P-theorie kan de resonantietoestand van de F-P-holte van het niet-gekrompen PNS worden geschreven als:

$$\delta =(2\pi /\lambda ) \cdot H \cdot n_{eff} + \varphi =m\pi ,$$ (8)

waar δ is de faseverschuiving, λ is de golflengte in de vrije ruimte, n _eff is de ERI van de equivalente homogene plaat van de PNS, φ is de extra fase en m is een geheel getal dat de resonantievolgorde aangeeft. Door gebruik te maken van de effectieve mediumtheorie [49], kan de ERI van het PNS worden geschat als:

$$n_{eff} =\sqrt {\frac{{\left[ {\left( {1 - f} \right)n_{a}^{2} + fn_{s}^{2} } \right] \left[ {fn_{a}^{2} + \left( {1 - f} \right)n_{s}^{2} } \right] + n_{s}^{2} }}{{2 \left[ {fn_{a}^{2} + \left( {1 - f} \right)n_{s}^{2} } \right]}}} ,$$ (9)

waar f is de vulfactor van de PNS, en f = 1 − 4π(r /Λ) ² .

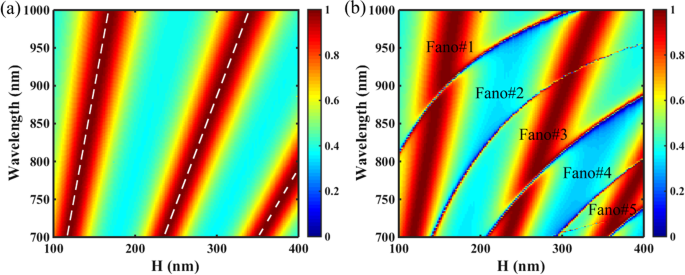
een Transmissie 2D-kaart van het PNS als functie van de plaathoogte H met Δ = 0 nm, de witte streepjeslijnen zijn de resultaten van het F–P-holtemodel. b Transmissie 2D-kaart van het PNS als functie van de plaathoogte H met Δ =  − 28 nm. Andere parameters zijn hetzelfde als in Afb. 1c

Door gebruik te maken van vergelijkingen. (8) en (9), de locaties van de F–P-resonantie van het niet-gekrompen PNS kunnen worden berekend als λ _F–P = 2π ·H·n _eff /(mπ -φ ). In de berekening, hoewel de extra fase φ kan niet worden behandeld als een constante omdat het duidelijk de faseverschuiving beïnvloedt δ , kunnen de waarden worden berekend met behulp van de lineaire aanpassingsmethode [50, 51]. Figuur 8a toont de transmissie 2D-kaart van de PNS met Δ = 0 nm, en de resultaten van de F–P-theorie worden aangegeven door de witte streepjeslijnen. Zoals weergegeven in figuur 8a, vallen de witte streepjeslijnen van het F–P-holtemodel samen met die van de transmissiepieken van de PNS, wat bevestigt dat het de F–P-resonantie is die de transmissie van de niet-gekrompen PNS in de spectrale regio van belang. Echter, zoals getoond in figuur 8b, worden voor de gekrompen PNS met Δ =  − 24 nm vijf Fano-resonanties met een hoge Q-factor geëxciteerd en bestaan ​​ze naast de F-P-resonanties, aangezien H wordt gevarieerd in het bereik van 100-400 nm , zijn de Fano-resonanties zo sterk dat ze de F–P-resonanties in het kruisingsgebied tussen de Fano- en F-P-resonanties splitsen. Volgens de plaatgolfgeleidertheorie zorgt de toename van de dikte van de fotonische kristalplaat voor meer lekkende modi die in de structuur worden begrensd [32, 52]; het aantal Fano-resonanties kan dus worden vergroot door alleen de dikte van de PNS te vergroten. Merk op dat de verschuiving van de tetrameriseerde gaten de ERI van de PNS niet zal veranderen, dus de locaties van de FP-resonanties blijven bijna hetzelfde voor zowel de niet-gekrompen als de gekrompen structuren.

Conclusies

Dual-band Fano-resonanties met een hoge Q-factor kunnen worden gerealiseerd door een relatief eenvoudige architectuur van PNS te gebruiken op basis van de excitatie van dubbele QBIC's. Door vier nanogaten van de PNS langs de diagonalen van het superrooster te verkleinen of uit te breiden, kunnen twee tegen symmetrie beschermde BIC's worden getransformeerd naar dual-band Fano-resonanties en kunnen hun locaties en hun Q-factoren flexibel worden afgestemd. De dual-band Fano-resonanties van de PNS zijn het resultaat van de resonante koppelingen tussen de elektrische toroidale dipolen of de magnetische toroidale dipolen, en hun correlaties tussen de far-field meervoudige decomposities en de near-field distributies van het superrooster zijn geverifieerd. De dual-band Fano-resonanties van de PNS hebben een polarisatie-onafhankelijk kenmerk en hun hoge Q-factorkenmerken zijn robuust tegen de variaties van de geometrische parameters. Door de hoogte van de PNS te vergroten, kan het aantal Fano-resonanties met een hoge Q-factor worden verbeterd, omdat meer lekkende modi door de structuur kunnen worden ondersteund. Onze resultaten geven meer vrijheden bij het afstemmen voor de realisatie van resonatoren met een hoge Q-factor met betere prestaties, wat een verdere stap kan zijn in de ontwikkeling van lasering, sensing en niet-lineaire fotonica.

Beschikbaarheid van gegevens en materialen

De datasets die tijdens het huidige onderzoek zijn gebruikt en/of geanalyseerd, zijn op redelijk verzoek verkrijgbaar bij de corresponderende auteur.

Afkortingen

Q-factor:

Kwaliteitsfactor

PNS:

Planaire nanogatplaat

BIC's:

Gebonden toestanden in het continuüm

NIR:

Nabij-infrarood

QBIC's:

Quasi-BIC's

FWHM:

Volledige breedte op halve maximum

ED:

Elektrische dipool

MD:

Magnetische dipool

TD:

Ringkern dipool

EQ:

Elektrische quadrupool

MQ:

Magnetische quadrupool

ERI:

Effectieve brekingsindex

F–P:

Fabry–Pérot