Afhankelijkheid van elektronische en optische eigenschappen van MoS2-multilagen van de tussenlaagkoppeling en Van Hove-singulariteit
Abstract
In dit artikel worden de structurele, elektronische en optische eigenschappen van MoS2 multilagen worden onderzocht door gebruik te maken van de first-principles methode. Tot zes lagen MoS2 zijn vergelijkend bestudeerd. De covalentie en ioniciteit in de MoS2 monolaag blijkt sterker te zijn dan die in de bulk. Aangezien het aantal lagen wordt verhoogd tot twee of meer dan twee, is bandsplitsing significant vanwege de koppeling tussen de lagen. We ontdekten dat lange plateaus ontstonden in de denkbeeldige delen van de diëlektrische functie \( {\varepsilon}_2^{xx}\left(\omega \right) \) en de gezamenlijke toestandsdichtheid (JDOS) van MoS2 meerlagen, vanwege de Van Hove-singulariteiten in een tweedimensionaal materiaal. Een, twee en drie kleine stapjes verschijnen op de drempels van zowel het lange plateau van \( {\varepsilon}_2^{xx}\left(\omega \right) \) als JDOS, voor respectievelijk monolaag, dubbellaag en drielaags . Naarmate het aantal lagen verder toenam, nam het aantal kleine stapjes toe en de breedte van de kleine stapjes dienovereenkomstig af. Vanwege de koppeling tussen de lagen zijn het langste plateau en het kortste plateau van JDOS respectievelijk van de monolaag en de bulk.
Inleiding
Molybdeendisulfide (MoS2 ) is een van de typische overgangsmetaaldichalcogeniden en wordt veel gebruikt als katalysator [1] en waterstofopslagmateriaal [2, 3]. Vanwege de sterke in-plane interacties en zwakke Van der Waals interacties tussen MoS2 atomaire lagen [4, 5], MoS2 kristallen staan al jaren bekend als een belangrijk vast smeermiddel [6, 7]. De monolaag MoS2 , zogenaamde 1H -MoS2 , is geëxfolieerd van bulk MoS2 door gebruik te maken van micromechanische splitsing [8]. De zogenaamde 2H -MoS2 (onder 1T , 2H , 3R ) is de meest stabiele structuur van bulk MoS2 [9, 10] en is een halfgeleider met een indirecte bandgap van 1,29 eV [4, 11, 12]. De monolaag MoS2 heeft ook veel aandacht getrokken vanwege zijn tweedimensionale karakter en grafeenachtige honingraatstructuur. Het is interessant dat monolaag MoS2 heeft een directe bandgap van 1,90 eV [4, 13] die kan worden gebruikt als een geleidend kanaal van veldeffecttransistoren [14]. Aan de andere kant beperkt de nulbandafstand van grafeen zijn toepassingen in optica en transistortoepassingen [15,16,17,18]. Bovendien tonen de theoretische en experimentele werken aan dat de elektronische bandgap kleiner wordt naarmate het aantal MoS2 lagen is vergroot [19,20,21,22]. Tussenlaagkoppeling van meerlaagse MoS2 is gevoelig voor laagdikte [21]. Enkele onderzoeken op de meerlaagse MoS2 zijn beschikbaar [19,20,21,22,23,24,25]; echter, de elektronische structuren en optische eigenschappen van meerlaagse MoS2 zijn nog steeds niet goed ingeburgerd, vooral voor de laagafhankelijke fysieke eigenschappen die verband houden met de koppeling tussen de lagen. Van Hove-singulariteit (VHS) speelt een belangrijke rol bij optische eigenschappen [26, 27]. De enige beschikbare kritische punten in tweedimensionale materialen zijn die van de P 0 (P 2 ) en P 1 type, die worden weergegeven als een stap en een logaritmische singulariteit [26, 27]. In dit artikel analyseren we de elektronische en optische eigenschappen van MoS2 gerelateerd aan Van Hove-singulariteit, laag voor laag en tot zes atomaire lagen.
Tegenwoordig zijn met succes eerste-principeberekeningen uitgevoerd om de structurele, elektronische en optische eigenschappen van een grote verscheidenheid aan materialen te bestuderen. In dit werk hebben we systematisch de elektronische en optische eigenschappen bestudeerd van monolaag, meerlaags en bulk MoS2 door gebruik te maken van ab initio berekeningen. Discussies over de optische eigenschappen worden benadrukt. Uit onze resultaten blijkt dat voor E ||x , hebben de denkbeeldige delen van de diëlektrische functie \( {\varepsilon}_2^{xx}\left(\omega \right) \) lange plateaus. Op deze drempels van deze plateaus vertonen \( {\varepsilon}_2^{xx}\left(\omega \right) \) van de monolaag, dubbellaag en drielaags respectievelijk één, twee en drie kleine stappen. Het denkbeeldige deel van de diëlektrische functie wordt ook geanalyseerd door de gezamenlijke toestandsdichtheid en de overgangsmatrixelementen. JDOS gecombineerd met de bandstructuren en de Van Hove-singulariteiten komen uitgebreid aan bod.
Methoden
De huidige berekeningen zijn uitgevoerd met behulp van het Vienna ab initio simulatiepakket (VASP) [28, 29], dat is gebaseerd op de dichtheidsfunctionaaltheorie, de vlakke-golfbasis en de projector augmented wave (PAW) representatie [30]. Het uitwisselingscorrelatiepotentieel wordt behandeld binnen de gegeneraliseerde gradiëntbenadering (GGA) in de vorm van Perdew-Burke-Ernzerhof (PBE) functioneel [31]. Om de zwakke tussenlaagattracties in dit gelaagde kristal in overweging te nemen, zijn PBE-D2-berekeningen [32] uitgevoerd die de semi-empirische van der Waals-correctie omvatten. Om nauwkeurigere bandhiaten te verkrijgen, worden in dit werk ook de Heyd-Scuseria-Ernzerhof hybride functionele (HSE06) [33,34,35,36]-berekeningen uitgevoerd. De golffuncties van alle berekende systemen worden uitgebreid in vlakke golven, met een kinetische energiegrens van 500 eV. Brillouin zone (BZ) integraties worden berekend met behulp van een speciale k -point sampling van het Monkhorst-Pack schema [37], met een 45 × 45 × 1 Γ -gecentreerd raster voor de monolaag en meerlaagse MoS2 en 45 × 45 × 11 raster voor de bulk MoS2 voor PBE-D2-berekeningen. Voor HSE06-berekeningen geldt een 9 × 9 × 1 Γ -gecentreerd raster wordt gebruikt voor de monolaag en meerlaagse MoS2 . Voor de monolaag en meerlaagse MoS2 , zijn alle berekeningen gemodelleerd door een supercel met een vacuümruimte van 35 Å in de Z -richting om de interacties tussen aangrenzende MoS2 . te vermijden platen. Alle atomaire configuraties zijn volledig ontspannen totdat de Hellmann-Feynman-krachten op alle atomen kleiner zijn dan 0,01 eV/Å. Onze spin-gepolariseerde berekeningen laten zien dat de bandstructuren van MoS2 meerlagen zijn nogal ongevoelig voor het spin-gepolariseerde effect (zie aanvullend bestand 1:figuur S1); daarom zijn alle gepresenteerde berekeningsresultaten gebaseerd op het non-spin-polarisatieschema.
Excitonische effecten in monolaag MoS2 zijn significant bevonden en zijn waargenomen door fotoluminescentie. We hebben het quasi-deeltje G0 . gebruikt W0 methode [38] en de Bethe-Salpeter-vergelijking (BSE) [39, 40] om rekening te houden met de excitonische effecten. De band gaps van monolaag MoS2 worden berekend op 2,32 en 2,27 eV voor de k -puntmazen van 15 × 15 × 1 en 24 × 24 × 1 Γ -gecentreerd raster, verkregen door de G0 W0 met SOC-berekeningen. De denkbeeldige delen van de diëlektrische functie worden getoond in Fig. 1, berekend op basis van zowel de G0 W0 en de G0 W0 + BSE-methoden. Er worden twee excitonpieken van 1,84 en 1,99 eV gevonden, wat goed overeenkomt met experimentele waarnemingen [4, 41]. Hoewel de G0 W0 +BSE-schema zou de excitonische effecten beter kunnen beschrijven, in dit artikel presenteren we alleen de resultaten (zonder excitonische pieken) onder de GGA-PBE-functionaliteit.
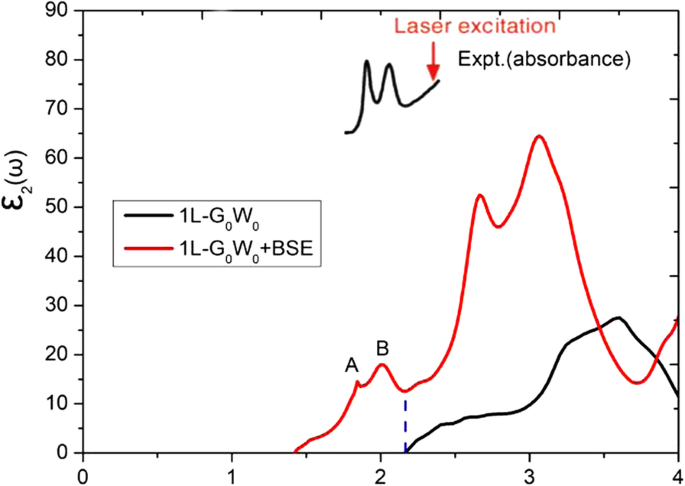
De denkbeeldige delen van de diëlektrische functie voor monolaag MoS2 , door de G0 . te gebruiken W0 en G0 W0 +BSE-methoden, respectievelijk. Het experimentele absorptiespectrum voor MoS2 wordt geëxtraheerd uit ref. [4]
Resultaten en discussie
Elektronische structuren van MoS2 Meerdere lagen
Kristallijne MoS2 komt van nature voor en heeft drie kristallijne typen:1T , 2H , en 3R , wat overeenkomt met kristallen met respectievelijk trigonale, hexagonale en rhomboëdrische primitieve eenheidscellen [9]. 2H -MoS2 staat bekend als de meest stabiele structuur [10]; daarom beschouwen we alleen de 2H type bulk MoS2 in dit werk. Bulk 2H -MoS2 heeft een zeshoekige gelaagde structuur bestaande uit lagen van molybdeenatomen omgeven door zes zwavelatomen, met tegenover elkaar opgestapelde S-Mo-S-platen (getoond in Fig. 2). De aangrenzende vellen in bulk 2H -MoS2 zijn zwak verbonden met zwakke van der Waals-interacties. Een monolaag MoS2 kan dan gemakkelijk van de bulk worden geëxfolieerd. De roosterconstanten van bulk MoS2 worden berekend als a =b =3.19Å, c =12,41 Å, die consistent zijn met de gerapporteerde waarden van a =b =3.18 Å, c =13,83 Å [18]. De geoptimaliseerde roosterconstanten voor monolaag MoS2 zijn a =b =3.19 Å, die in overeenstemming zijn met de bulk MoS2 . Zoals weergegeven in Tabel 1 zijn de berekende roosterconstanten in de a , b aanwijzingen zijn hetzelfde voor verschillende aantal lagen van MoS2 . Het werd ook gemeld door Kumar et al. [19] dat de roosterconstanten (a, b ) van monolaag MoS2 zijn bijna identiek aan de bulk.
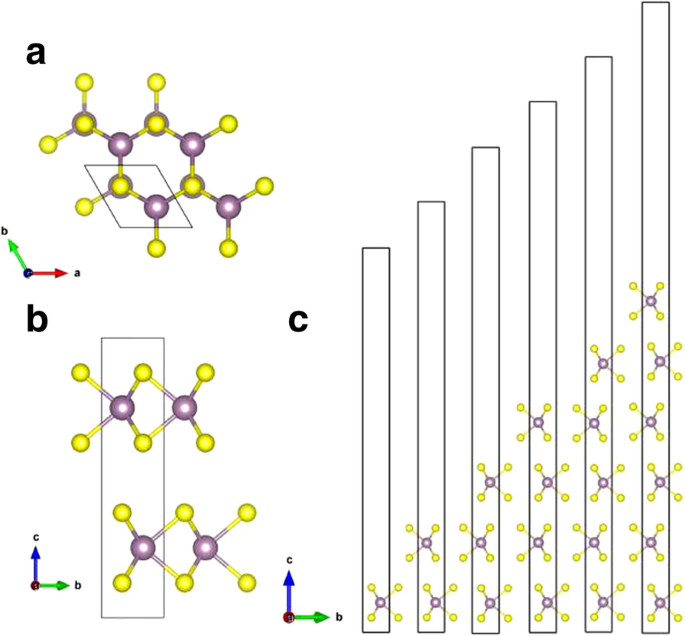
een Bovenaanzicht en b zijaanzicht van bulk-MoS2 . c Zijaanzicht van monolaag, dubbellaag, drielaags, evenals vier-, vijf- en zeslaagse structuren van MoS2 . Een eenheidscel wordt weergegeven in b . Paarse en gele ballen vertegenwoordigen respectievelijk Mo- en S-atomen
Figuur 3 toont de berekende bandstructuren en elektronische toestandsdichtheid (DOS) van verschillende aantallen lagen MoS2 . Resultaten voor monolaag, dubbellaag, drielaags en vierlaags evenals bulk MoS2 worden gegeven in Fig. 3, terwijl de resultaten voor vijflaags en zeslaags MoS2 zijn zeer vergelijkbaar met die van vierlaags en bulk. Voor monolaag MoS2 , verschijnen zowel het valentiebandmaximum (VBM) als het geleidingsbandminimum (CBM) op het K-punt van de BZ, met een directe bandgap van 1,64 eV. Voor dubbellaagse en drielaagse MoS2 , zowel de VBM lokaliseren op Γ punt terwijl zowel de CBM op K punt liggen, wat indirecte gaten veroorzaakt van respectievelijk 1,17 en 1,08 eV. Echter, aangezien het aantal MoS2 lagen neemt toe tot vier en boven vier, alle meerlagen MoS2 tonen dezelfde karakters die de VBM lokaliseert op Γ punt terwijl de CBM tussen Γ en K punten ligt, wat hetzelfde is als in de bulk. Indirecte bandgaps zijn 1,03 eV, 1,01 eV, 0,99 eV, 0,93 eV voor vier-, vijf-, zeslaags MoS2 , en bulk, respectievelijk. Zowel de PBE-D2- als de HSE06-berekeningen (tabel 1) laten zien dat de fundamentele bandgap monotoon toeneemt wanneer het aantal MoS2 lagen neemt af, wat te wijten is aan een grote opsluiting van elektronen in de plaat [4, 5, 19, 42]. Bovendien, wanneer de bulk MoS2 plaat wordt gereduceerd tot een enkellaags, het verandert in een directe bandgap-halfgeleider, zoals eerder vermeld, de bulk MoS2 is een indirecte gap halfgeleider. In Fig. 3a plotten bandstructuren van bulk MoS2 tonen splitsing van banden (in vergelijking met die van monolaag MoS2 ), voornamelijk rond de  -punt, als gevolg van koppeling tussen de lagen [16]. Bandstructuren voor twee lagen (2L) en meer dan 2L MoS2 vertonen een vergelijkbare splitsing van banden als gevolg van de koppeling tussen de lagen. De splitsing van banden in de bulk is echter iets significanter dan die in de meerlaagse MoS2 , wat wijst op een (iets) sterkere tussenlaagkoppeling in de bulk dan in de meerlagen. Aan de andere kant is de splitsing van banden in de buurt van punt K in BZ erg klein. De elektronische toestanden op punt K voor de hoogst bezette band bestaan voornamelijk uit d xy en \( {d}_{x^2-{y}^2} \) orbitalen van Mo-atomen, evenals kleine delen van (p x , p j ) -orbitalen van S-atomen (getoond in figuur 4b). De Mo-atomen bevinden zich in de middelste laag van de S-Mo-S-plaat, wat een verwaarloosbare koppeling tussen de lagen veroorzaakt op het K-punt (aangezien de dichtstbijzijnde atomen tussen MoS2 lagen zijn S en S). Zoals getoond in Fig. 4, kan een sterkere tussenlaagkoppeling op punt Γ worden gevonden in vergelijking met die in punt K, aangezien elektronische toestanden op punt Γ voor de hoogst bezette band worden gedomineerd door \( {d}_{z^2} \ ) orbitalen van Mo-atomen en p z orbitalen van S-atomen. Daarom is SS-koppeling (tussenlaagkoppeling) duidelijk sterker op punt Γ dan die op punt K. Onze resultaten zijn consistent met ander theoretisch werk [21]. Over het algemeen is de elektronische toestandsdichtheid van MoS2 zijn vergelijkbaar met die van bulk MoS2 (zie Fig. 3), aangezien bulk MoS2 is eigenlijk een gelaagd materiaal met zwakke interacties tussen de MoS2 lagen.
-punt, als gevolg van koppeling tussen de lagen [16]. Bandstructuren voor twee lagen (2L) en meer dan 2L MoS2 vertonen een vergelijkbare splitsing van banden als gevolg van de koppeling tussen de lagen. De splitsing van banden in de bulk is echter iets significanter dan die in de meerlaagse MoS2 , wat wijst op een (iets) sterkere tussenlaagkoppeling in de bulk dan in de meerlagen. Aan de andere kant is de splitsing van banden in de buurt van punt K in BZ erg klein. De elektronische toestanden op punt K voor de hoogst bezette band bestaan voornamelijk uit d xy en \( {d}_{x^2-{y}^2} \) orbitalen van Mo-atomen, evenals kleine delen van (p x , p j ) -orbitalen van S-atomen (getoond in figuur 4b). De Mo-atomen bevinden zich in de middelste laag van de S-Mo-S-plaat, wat een verwaarloosbare koppeling tussen de lagen veroorzaakt op het K-punt (aangezien de dichtstbijzijnde atomen tussen MoS2 lagen zijn S en S). Zoals getoond in Fig. 4, kan een sterkere tussenlaagkoppeling op punt Γ worden gevonden in vergelijking met die in punt K, aangezien elektronische toestanden op punt Γ voor de hoogst bezette band worden gedomineerd door \( {d}_{z^2} \ ) orbitalen van Mo-atomen en p z orbitalen van S-atomen. Daarom is SS-koppeling (tussenlaagkoppeling) duidelijk sterker op punt Γ dan die op punt K. Onze resultaten zijn consistent met ander theoretisch werk [21]. Over het algemeen is de elektronische toestandsdichtheid van MoS2 zijn vergelijkbaar met die van bulk MoS2 (zie Fig. 3), aangezien bulk MoS2 is eigenlijk een gelaagd materiaal met zwakke interacties tussen de MoS2 lagen.
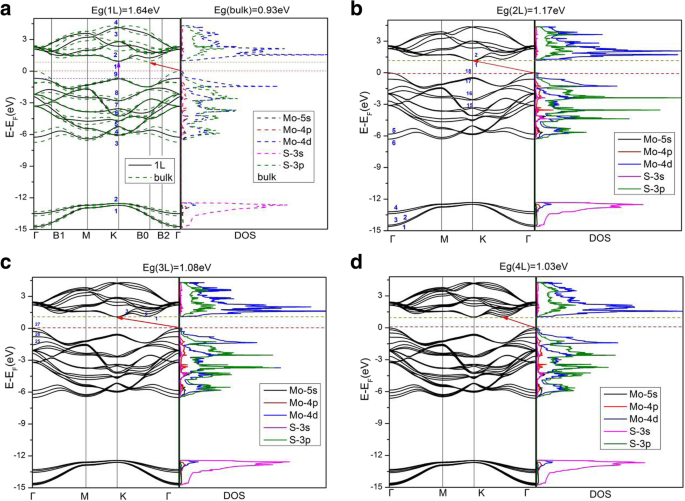
Berekende bandstructuren en toestandsdichtheid van a monolaag (volledige lijnen) en bulk (streepjeslijnen), b dubbellaags, c drielaags, en d vierlaagse MoS2 . In een , zijn de hoogste bezette banden voor bulk en monolaag op punt K ingesteld op dezelfde energie. Geleidingsband minimale bulk is op punt B0
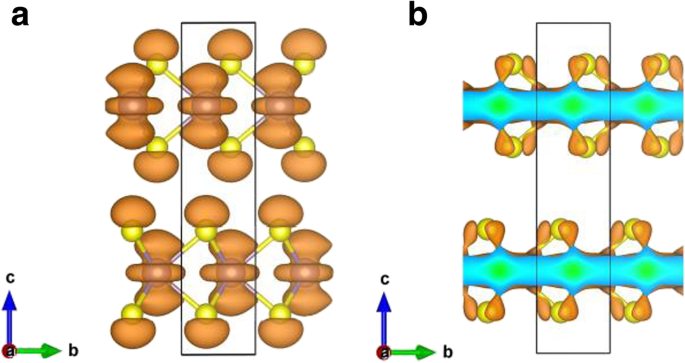
De ladingsverdelingen van de hoogst bezette band bij a punt  en b punt K voor bulk MoS2 . De iso-oppervlaktewaarde is ingesteld op 0,004 e/Å
3
en b punt K voor bulk MoS2 . De iso-oppervlaktewaarde is ingesteld op 0,004 e/Å
3
Om de bindende aard in de monolaag MoS2 . grondig te onderzoeken , wordt de vervormingsladingsdichtheid getoond in Fig. 5a. De vervormingsladingsdichtheid wordt gegeven door Δρ 1 (r ) = ρ (r ) − ∑μ ρ atoom (r − R μ ) waar ρ (r ) is de totale ladingsdichtheid en ∑μ ρ atoom (r − R u ) staat voor de superpositie van onafhankelijke atomaire ladingsdichtheden. De resultaten tonen aan dat de binding in de MoS2 monolaag wordt gekenmerkt door duidelijke covalente (vaste contourlijnen tussen de Mo-S-atomen), evenals sterke ionische interacties (weergegeven door afwisselende gebieden met gestippelde en vaste contouren). Om de hechtsterkte in de monolaag MoS2 . te zien in vergelijking met die in de bulk, de verschillen in ladingsdichtheid tussen monolaag en bulk MoS2 , Δρ 2 (r ), wordt ook weergegeven in Fig. 5b. Het verschil in ladingsdichtheid wordt gedefinieerd als Δρ 2 (r ) = ρ 1L (r ) − ρ bulk (r ), waar ρ 1L (r ) en ρ bulk (r ) zijn de totale ladingsdichtheden van monolaag en bulk MoS2 , respectievelijk. Figuur 5b geeft een sterkere elektronische binding in de monolaag aan dan die in de bulk, wat wordt weerspiegeld door de grotere ladingsaccumulatie (vaste contourlijnen) tussen de Mo-S-atomen in de monolaag, evenals door sterkere ionische binding in de monolaag MoS2 aangezien de afwisselende gebieden van gestippelde en effen contouren in figuur 5b belangrijker zijn dan die in de bulk. Bovendien geeft de ladingsverschillenplot (figuur 5b) aan dat het Mo-atoom van de monolaag meer elektronen verloor dan het Mo-atoom in de bulk; daarom is de ioniciteit van monolaag sterker dan bulk. Er moet echter worden opgemerkt dat de orde van grootte van de ladingsverschillen in figuur 5b vrij klein is (het contourinterval in figuur 5b is slechts 2,5 × 10 −4 e/Å 3 ). Afgaande op het kwantumbegrenzingseffect, nogmaals, de interactie tussen de lagen van monolaag zou sterker moeten zijn dan bulk. Daarom wordt verwacht dat de bandgap van de monolaag (1,64 eV) groter is dan de bulk (0,93 eV). Kwantumopsluiting neemt af met het toenemende aantal lagen [4, 42], wat de koppeling tussen de lagen verbetert en de interactie tussen de lagen vermindert. Dus de band gap van MoS2 neemt af met de toename van de tussenlaagkoppeling. De herverdelingen van de tussenlaagse ladingsdichtheid voor dubbellaagse MoS2 , Δρ 3 (r ), worden ook weergegeven in Fig. 5c. De Δρ 3 (r ) wordt gegeven door Δρ 3 (r ) = ρ 2L (r ) − ρ laag1 (r ) − ρ laag2 (r ), waar ρ 2L (r ), ρ laag1 (r ), ρ laag2 (r ) zijn de ladingsdichtheden van de dubbellaagse MoS2 , de eerste laag van dubbellaagse MoS2 en de tweede laag van dubbellaagse MoS2 , respectievelijk. De ladingsdichtheden van laag1 en laag2 van dubbellaagse MoS2 worden berekend met behulp van de overeenkomstige structuur in dubbellaagse MoS2 . Overboeking van MoS2 lagen (dubbellaag) naar het tussengebied tussen de MoS2 lagen zijn duidelijk te zien in figuur 5c, weergegeven als ononderbroken contourlijnen. De ionische interacties tussen atomaire lagen in dubbellaagse MoS2 zijn ook duidelijk, zoals blijkt uit de afwisselende gebieden van gestippelde en effen contouren. Nogmaals, de orde van grootte van de ladingsdichtheden tussen de lagen, Δρ 3 (r ), zijn erg klein (het contourinterval is slechts 2,5 × 10 -4 e/Å 3 ). Over het algemeen zijn de herverdelingen van de ladingsdichtheid tussen de lagen in 2L, 3L, ..., bulk MoS2 systemen lijken allemaal erg op elkaar.
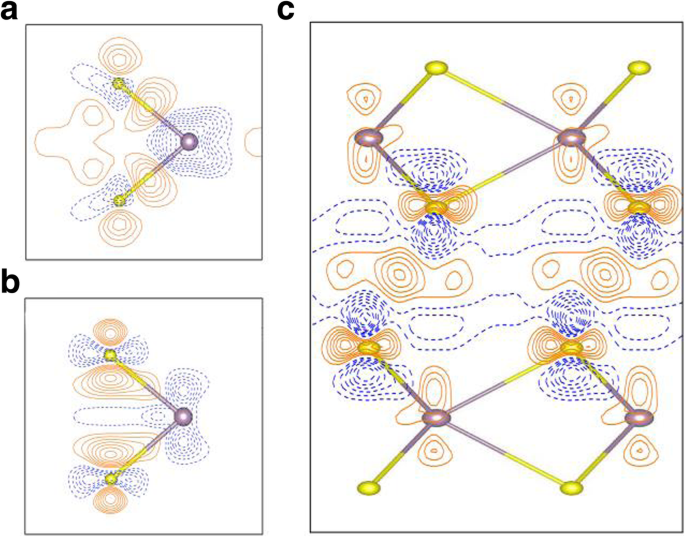
een Vervormingsladingsdichtheid, Δρ 1 (r ) = ρ (r ) − ∑μ ρ atoom (r − R μ ), in de monolaag MoS2 . b Verschillen tussen de ladingsdichtheden van monolaag en de overeenkomstige laag bulk. c De herverdeling van de ladingsdichtheid tussen de lagen van MoS2 . Contourinterval van a is 2,5 × 10 −2 e/Å 3 , terwijl beide van b en c zijn 2,5 × 10 −4 e/Å 3 . Effen oranje en blauwe stippellijnen komen overeen met Δρ> 0 en Δρ < 0, respectievelijk
Optische eigenschappen van MoS2 Meerdere lagen
Zodra de elektronische grondtoestandstructuren van een materiaal zijn verkregen, kunnen de optische eigenschappen worden onderzocht. Het imaginaire deel van de diëlektrische functie \( {\varepsilon}_2^{\alpha \beta}\left(\omega \right) \) wordt bepaald door de volgende vergelijking [43]:
$$ {\displaystyle \begin{array}{c}{\varepsilon}_2^{\alpha \beta}\left(\omega \right)=\frac{4{\pi}^2{e}^2} {\Omega}{\lim}_{q\to 0}\frac{1}{q^2}\underset{c,v,k}{\Sigma}2{w}_k\delta \left({E }_{ck}-{E}_{vk}-\mathrm{\hslash}\omega \right)\\ {}\times \left\langle {u}_{ck+{e}_{\alpha }q }|{u}_{vk}\right\rangle \left\langle {u}_{ck+{e}_{\beta }q}|{u}_{vk}\right\rangle \ast \end{ reeks}} $$ (1)waar de indices α en β duiden Cartesiaanse aanwijzingen aan, c en v verwijzen naar geleidings- en valentiebanden, E ck en E vk zijn de energieën van respectievelijk geleidingsbanden en valentiebanden. De Kramers-Kronig-inversie kan worden toegepast om het reële deel van de diëlektrische functie \( {\varepsilon}_1^{\alpha \beta}\left(\omega \right) \) bepaald door het imaginaire deel \( {\ varepsilon}_2^{\alpha \beta}\left(\omega \right) \):
$$ {\varepsilon}_1^{\alpha \beta}\left(\omega \right)=1+\frac{2}{\pi }P{\int}_0^{\infty}\frac{\varepsilon_2 ^{\alpha \beta}\left(\omega \hbox{'}\right)\omega \hbox{'}}{\omega {\hbox{'}}^2-{\omega}^2+ i\ eta} d\omega \hbox{'} $$ (2)waarin P de hoofdwaarde vertegenwoordigt. Sinds MoS2 heeft een uniaxiale structuur, ε xx (ω ) is dan identiek aan ε yy (ω ). In dit werk hoeven we alleen de elektrische vector E . te bespreken die parallel is aan de x-y vliegtuig, d.w.z. E|| x is parallel aan de MoS2 x-y vliegtuig.
Voor het onderzoeken van gedetailleerde optische spectra van MoS2 systeem, de absorptiecoëfficiënt α (ω ) en de reflectiviteit R (ω ) werden berekend door het reële deel ε 1 (ω ) en het denkbeeldige deel 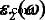 van de diëlektrische functie. Vergelijkingen van genoemde parameters worden hieronder weergegeven:
van de diëlektrische functie. Vergelijkingen van genoemde parameters worden hieronder weergegeven:
Als het matrixelement \( \left\langle {u}_{ck+{e}_{\alpha }q}|{u}_{vk}\right\rangle \) erg langzaam varieert als k -vector, de term \( \left\langle {u}_{ck+{e}_{\alpha }q}|{u}_{vk}\right\rangle \left\langle {u}_{ck+{ e}_{\beta }q}|{u}_{vk}\right\rangle \ast \) in Vgl. (1) kan buiten de sommatie worden genomen. In verg. (1), het grootste deel van de spreiding in \( {\varepsilon}_2^{\alpha \beta}\left(\omega \right) \) is te wijten aan de sommatie over de deltafunctie δ (E ck − E vk − ℏω ). Deze sommatie kan worden omgezet in een integratie over energie door een gezamenlijke toestandsdichtheid (JDOS) te definiëren [25, 44],
$$ {J}_{cv}\left(\omega \right)=\frac{1}{4{\pi}^3}\int \frac{dS_k}{\nabla_k\left({E}_{ ck}-{E}_{vk}\right)} $$ (5)waarin ℏω is gelijk aan E ck − E vk , S k vertegenwoordigt het constante energie-oppervlak aangegeven met E ck − E vk = ℏω = const. De gezamenlijke toestandsdichtheid J cv (ω ) wordt geassocieerd met de overgangen van de valentiebanden naar de geleidingsbanden en de grote pieken in J cv (ω ) zal zijn oorsprong vinden in het spectrum waar ∇k (E ck − E vk ) ≈ 0. Punten in k -spatie waar ∇k (E ck − E vk ) = 0 worden kritieke punten of van Hove-singulariteiten (VHS) genoemd, en E ck − E vk worden kritische puntenergieën genoemd [26, 27]. De kritieke punten ∇k E ck = ∇k E vk = 0 komt meestal alleen voor op punten met een hoge symmetrie, terwijl kritieke punten ∇k E ck = ∇k E vk ≠ 0 kan voorkomen op alle algemene punten in de Brillouin-zone [27, 45]. In het tweedimensionale geval zijn er drie soorten kritieke punten, namelijk P 0 (minimumpunt), P 1 (zadelpunt), en P 2 (maximaal punt). Op de punten P 0 of P 2 , trad er een singulariteit van de stapfunctie op in JDOS, terwijl op het zadelpunt P 1 , werd JDOS beschreven door een logaritmische singulariteit [27]. In meer detail, de E c (k x , k j ) − E v (k x , k j ) kan worden uitgebreid in een Taylor-reeks over het kritieke punt. De uitbreiding beperken tot kwadratische termen, waarbij de lineaire term niet optreedt vanwege de eigenschap van de singulariteit, hebben we dan
$$ {E}_c\left({k}_x,{k}_y\right)-{E}_v\left({k}_x,{k}_y\right)={E}_0+\frac{\ mathrm{\hslash}}{2}\left({b}_x\frac{k_x^2}{m_x}+{b}_y\frac{k_y^2}{m_y}\right) $$ (6)Daarom komen er drie soorten kritieke punten naar voren. Voor P 0 , (b x > 0, b j > 0), voor P 1 , (b x > 0, b j < 0) of (b x < 0, b j > 0), en voor P 2 , (b x < 0, b j < 0). In dit artikel, voor het geval van MoS2 meerdere lagen, alleen de P 0 kritisch punt is betrokken.
Figuur 6a geeft de denkbeeldige delen van de diëlektrische functie, \( {\varepsilon}_2^{xx}\left(\omega \right) \), van MoS2 meerdere lagen voor E ||x. We hebben een interessant fenomeen gevonden dat de denkbeeldige delen van de diëlektrische functie \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateaus hebben, en de plateaus van verschillende lagen van MoS2 zijn bijna gelijk in het bereik van 1,75 eV ~ 2,19 eV. Van de drempelenergie tot 1,75 eV, \( {\varepsilon}_2^{xx}\left(\omega \right) \) zijn behoorlijk verschillend voor verschillende multilagen van MoS2 . De drempel- en eindenergieën van de plateaus in verschillende lagen zijn verschillend, vooral het energiebereik van het \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateau van de monolaag is aanzienlijk breder dan die van andere meerlagen. De drempelenergie van monolaag MoS2 diëlektrische functie is gelijk aan de directe bandgap van 1,64 eV. De drempelenergie van de dubbellaagse diëlektrische functie is echter niet de indirecte bandgap van 1,17 eV, maar het minimum van de directe energiekloof van 1,62 eV tussen de valentie- en geleidingsbanden. Dit komt omdat we alleen de overgangen tussen valentie- en geleidingsbanden bestuderen met dezelfde elektronengolfvector, die worden geclassificeerd als directe optische overgangen [36, 47]. Als het aantal MoS2 lagen verhoogd tot 4, vonden we dat \( {\varepsilon}_2^{xx}\left(\omega \right) \) van meerlaagse MoS2 systemen waren bijna niet te onderscheiden van bulk. Daarom bespreken we hier in detail alleen de plateaus van de monolaag, dubbellaag en drielaags, evenals bulk MoS2 . De \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateaus van monolaag, dubbellaag, drielaags en bulk MoS2 eindigde op respectievelijk 2,57 eV, 2,28 eV, 2,21 eV en 2,19 eV. Om dit nauwkeuriger uit te leggen, JDOS van monolaag, dubbellaag, drielaags en bulk MoS2 worden getoond in Fig. 7. Vanaf Fig. 7 zijn de plateaus ook weergegeven in de JDOS. De plateaus van monolaag, dubbellaag en drielaags JDOS eindigden op respectievelijk 2,57 eV, 2,28 eV en 2,21 eV, wat precies hetzelfde is als die in hun \( {\varepsilon}_2^{xx}\left(\omega \right ) \). Voor bulk MoS2 , het plateau van JDOS eindigde op 2,09 eV, wat iets kleiner is dan 2,19 eV in de diëlektrische functie \( {\varepsilon}_2^{xx}\left(\omega \right) \).
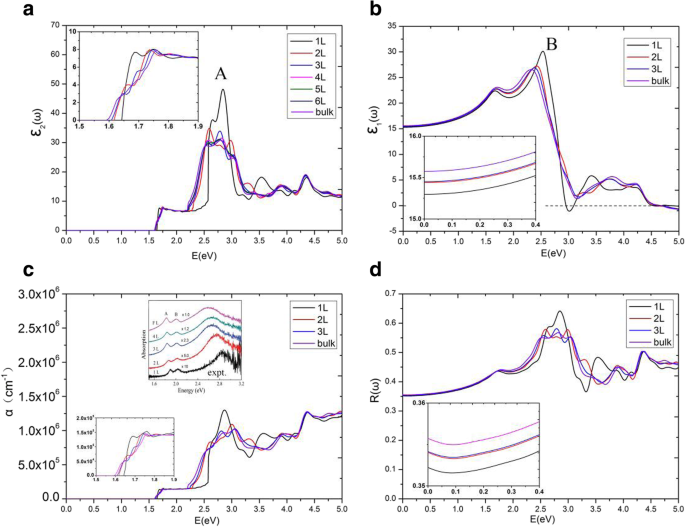
een De denkbeeldige delen van de diëlektrische functie, b de echte delen van de diëlektrische functie, c de absorptiecoëfficiënten, en d de reflectiviteitsspectra, voor verschillende aantallen MoS2 lagen. De inzet in c toont ook de experimentele gegevens [46]
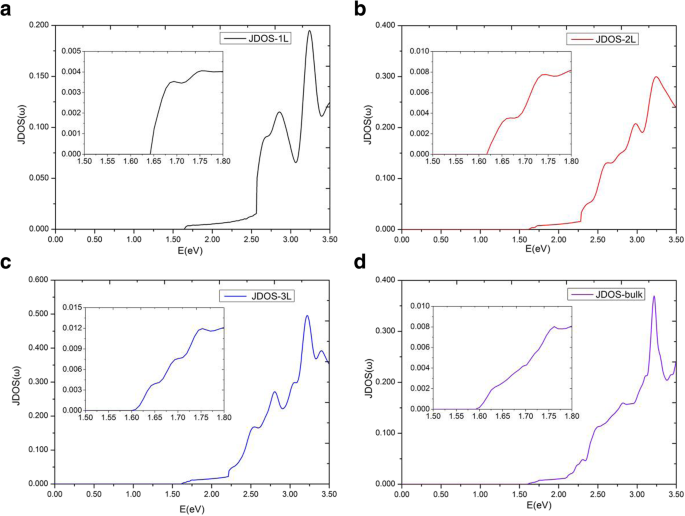
Gezamenlijke toestandsdichtheid voor de monolaag, bilaag, drielaagse en bulk MoS2
Om de elektronische overgangen nauwkeurig te analyseren en voor een gedetailleerde analyse van de diëlektrische functie \( {\varepsilon}_2^{xx}\left(\omega \right) \), de directe energiehiaten, ΔE(NC − NV), tussen geleidings- en valentiebanden van monolaag, dubbellaag, drielaags en bulk MoS2 worden weergegeven in Fig. 8. De notaties NC en NV vertegenwoordigen de ordinale nummers van geleidings- en valentiebanden. Vandaar dat NC =1, 2 en 3 de laagste, de op één na laagste en de op twee na laagste onbezette materiaalband aanduiden. Aan de andere kant duiden NV =9, 18 en 27 (die afhankelijk is van het aantal elektronen in de eenheidscel) de hoogste bezette band aan van monolaag, dubbellaag en drielaags MoS2 , respectievelijk. Voor monolaag, in het gebied van 0 ~ 2,57 eV, blijken de elektronische overgangen alleen te worden bijgedragen van de hoogste bezette band NV =9 tot de laagste onbezette band NC =1. Uit figuur 8a verschijnt een minimum op een hoog symmetriepunt K en de drempel van JDOS (Fig. 7a) verschijnt op 1,64 eV, wat eigenlijk de directe bandgap is van de monolaag MoS2 . In de buurt van het hoge symmetriepunt K is de curve van ΔE(NC = 1 − NV = 9) vergelijkbaar met een parabool voor monolaag MoS2 . Daarom, ∇k (E ck − E vk ) = 0 op K punt, wat een kritiek punt betekent op punt K met hoge symmetrie. In een tweedimensionale structuur behoort dit kritieke punt tot P 0 type singularity [27], en daarom leidt het tot een stap in de JDOS. De drempelenergie van het JDOS-plateau wordt dus gevonden bij kritieke puntenergie 1,64 eV. De eindenergie van het JDOS-plateau is bijna 2,57 eV, wat het gevolg is van het verschijnen van twee P 0 typ singulariteiten in punt B1 (k =(0,00, 0,16, 0,00)) en punt B2 (k =(− 0.10, 0.20, 0.00)). De hellingen van de ΔE(NC = 1 − NV = 9) curve nabij de twee kritische punten B1 en B2 zijn erg klein, wat aanleiding geeft tot een snelle toename van JDOS (zie Vgl. (5)). De belangrijkste kritieke punten voor deze lange JDOS-plateaus worden vermeld in tabel 2, inclusief type, locatie, overgangsbanden en de directe energiekloof ΔE (NC-NV). Verder vonden we dat ∇k E ck = ∇k E vk = 0 vond plaats op hoog symmetriepunt K waar de hellingen van de valentie- en geleidingsbanden horizontaal zijn. Terwijl ∇k E ck = ∇k E vk ≠ 0 gebeurde op de punten B1 en B2, wat betekent dat hellingen van twee banden evenwijdig zijn. Tegelijkertijd laat analyse van de bandstructuren en directe energiehiaten (zie Fig. 8a) voor de monolaag zien dat, wanneer de directe energiekloof ΔE lager is dan 2,65 eV, alleen de overgangen tussen NV =9 en NC =1 bijdragen aan JDOS; wanneer de ΔE groter is dan 2,65 eV, beginnen de overgangen van NV =9 naar NC =2 ook bij te dragen aan JDOS; terwijl wanneer de ΔE boven 2,86 eV komt, de NV =9 naar NC =3 overgangen effect hebben op JDOS. Opgemerkt moet worden dat voor energie groter dan 2,65 eV, veel banden in Fig. 8a zullen bijdragen aan JDOS. JDOS van monolaag MoS2 vertoont een plateau in het bereik van 1,64 ~ 2,57 eV en de variatie van de uitdrukking |Mvc | 2 /ω 2 blijkt in dit bereik klein te zijn. Volgens verg. (1) en (5), het imaginaire deel van de diëlektrische functie \( {\varepsilon}_2^{xx}\left(\omega \right) \) wordt voornamelijk bepaald door de JDOS en de overgangsmatrixelementen, dit geeft a similar plateau for the imaginary part of dielectric function \( {\varepsilon}_2^{xx}\left(\omega \right) \) as compared to JDOS.
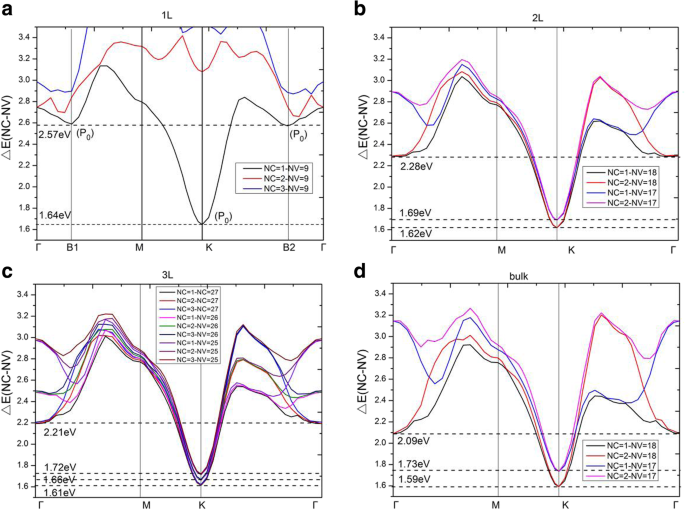
Direct energy gaps, ΔE(NC − NV), between conduction and valence bands for the a monolayer, b bilayer, c trilayer, and d bulk MoS2 . een –d There are three, six, twelve, and six critical points in interband transitions for the monolayer, bilayer, trilayer, and bulk MoS2 , respectievelijk
For bilayer MoS2 , in the region of 0 ~ 2.28 eV (the endpoint of JDOS plateau), the electronic transitions are contributed to NV =17, 18 to NC =1, 2. The minimum energy in ΔE(NC − NV) is situated at the K point with a gap of 1.62 eV. In Fig. 8b, similar to monolayer MoS2 , bilayer MoS2 holds two parabolic curves going upward (which come from ΔE(NC = 1 − NV = 18) and ΔE(NC = 2 − NV = 18)) at K point. Therefore, there are two P 0 type singularities (∇k (E ck − E vk ) = 0) at K point, causing a step in the JDOS. The critical point energies are both 1.62 eV, this is because that the conduction bands (NC =1 and NC =2) are degenerate at point K (as shown in Fig. 3b), which results in the same direct energy gap between transitions of NV =18 to NC =1 and NV =18 to NC =2. From Fig. 8b, as the direct energy gap is increased to 1.69 eV, two new parabolas (which come from ΔE(NC = 1 − NV = 17) and ΔE(NC = 2 − NV = 17)) appear and two new singularities emerge again at K point in the direct energy gap graph, leading to a new step in JDOS for bilayer MoS2 (see Fig. 7b). As a result, the JDOS of the bilayer MoS2 has two steps around the threshold of long plateau (see inset in Fig. 7b). Two parabolas (in Fig. 8b) contribute to the first step and four parabolas contribute to the second step in JDOS. It means that the value of the second step is roughly the double of the first one. As the ΔE reaches to 2.28eV, two new singularities appear at Γ point (where interband transitions come from Γ(NV =18→NC =1) and Γ(NV =18→NC =2)), which have great contribution to the JDOS and bring the end to the plateau. Our calculations demonstrate that ∇k E ck = ∇k E vk = 0 are satisfied not only at high symmetry point K, but also at high symmetry point Γ. Similar to the case of monolayer, we found that the term of |Mvc | 2 /ω 2 is a slowly varying function in the energy range of bilayer JDOS plateau; hence, \( {\varepsilon}_2^{xx}\left(\omega \right) \) of bilayer have a similar plateau in the energy range.
For trilayer MoS2 , in the region of 0 ~ 2.21 eV, the JDOS are contributed from electronic transitions of NV =25, 26, and 27 to NC =1, 2, and 3. As shown in Fig. 8c, trilayer MoS2 have nine singularities at three different energies (ΔE =1.61 eV, 1.66 eV, and 1.72 eV, respectively) at the K point. Figure 3c depicts that the conduction bands (NC =1, 2, 3) are three-hold degenerate at point K; this means that there are three singularities at each critical point energy. According to our previous analysis, the JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) of trilayer MoS2 will show three steps near the thresholds of the long plateaus, the endpoints of the long plateaus of trilayer JDOS, and \( {\varepsilon}_2^{xx}\left(\omega \right) \) are then owing to the appearance of three singularities at Γ point with ΔE =2.21 eV (see Fig. 7c), which come from the interband transitions of Γ(NV =27→NC =1, 2, 3).
For bulk MoS2 , the thresholds of \( {\varepsilon}_2^{xx}\left(\omega \right) \) and JDOS are also located at K point, with the smallest ΔE(NC − NV) equals to 1.59 eV. Nevertheless, there is no obvious step appeared in the thresholds of plateaus for both the \( {\varepsilon}_2^{xx}\left(\omega \right) \) and JDOS (see Fig. 6a and Fig. 7d). Based on the previous analysis, the number of steps in the monolayer, bilayer, and trilayer MoS2 are 1, 2, and 3, respectively. As the number of MoS2 layers increases, the number of steps also increases in the vicinity of the threshold energy. Thus, in the bulk MoS2 , the JDOS curve is composed of numerous small steps around the threshold energy of the long plateau, and finally the small steps disappear near the threshold energy since the width of the small steps decreases. In the region of 0 ~ 2.09 eV, the electron transitions of bulk MoS2 are contributed to NV =17, 18 to NC =1, 2. The 2.09 eV is the endpoint of JDOS plateau of bulk MoS2 , which is attributed to two singularities, i.e., the interband transitions of Γ(NV =18→NC =1) as well as Γ(NV =18→NC =2), as presented in Fig. 8d. However, the plateau endpoint of the imaginary part of dielectric function \( {\varepsilon}_2^{xx}\left(\omega \right) \) is 2.19 eV, which is greater than the counterpart of JDOS (e.g., 2.09 eV). Checked the transition matrix elements, it verified that some transitions are forbidden by the selection rule in the range of 2.09 eV to 2.19 eV. Therefore, the imaginary part of the dielectric function \( {\varepsilon}_2^{xx}\left(\omega \right) \) is nearly invariable in the range of 2.09 ~ 2.19 eV. As a result, the plateau of \( {\varepsilon}_2^{xx}\left(\omega \right) \) of bulk MoS2 is then 1.59 ~ 2.19 eV.
It has been shown that these thresholds of the JDOS plateaus are determined by singularities at the K point for all of the studied materials, see Fig. 8. The endpoint energy of the monolayer JDOS plateau is determined by two critical points at B1 and B2 (Fig. 8a). Nevertheless, the endpoint energies of bilayer, trilayer, and bulk JDOS plateaus are all dependent on the critical points at Γ(Fig. 8b–d). The interlayer coupling near point Γ is significantly larger than the near point K for all the systems of multilayer MoS2 . The smallest direct energy gap decreases and the interlayer coupling increases as the number of layers grow. With the layer number increases, a very small decrease of direct energy gap at point K and a more significant decrease of direct energy gap at point Γ can be observed, as a result, a faint red shift in the threshold energy and a bright red shift in the end of both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateaus can also be found. For monolayer MoS2 , the smallest ΔE(NC − NV) at point Γ is 2.75 eV which is larger than that at point B1 (or point B2) with a value around 2.57 eV. When it goes to multilayer and bulk MoS2 , the strong interlayer coupling near point Γ makes the smallest ΔE(NC − NV) at Γ less than those at point B1 (or point B2). Hence, monolayer owns the longest plateau of JDOS, which is between 1.64 eV and 2.57 eV. The shortest plateau of JDOS (from 1.59 eV to 2.09 eV) is shown in the bulk.
As the energy is increased to the value larger than the endpoint of long platform of the dielectric function, a peak A can be found at the position around 2.8 eV, for almost all the studied materials (Fig. 6a). The width of peak A for monolayer is narrower compared with those of multilayer MoS2; however, the intensity of peak A for monolayer is found to be a little stronger than multilayers. The differences between the imaginary parts of dielectric function for the monolayer and multilayer MoS2 are evident, on the other hand, the differences are small for multilayer MoS2 .
In order to explore the detailed optical spectra of MoS2 multilayers, the real parts of the dielectric function ε 1 (ω ), the absorption coefficients α (ω ), and the reflectivity spectra R (ω ) are presented in Fig. 6b–d. Our calculated data of bulk MoS2 for the real and imaginary parts of the dielectric function, ε 1 (ω ) and ε 2 (ω ), the absorption coefficient α (ω ) and the reflectivity R (ω ) agree well with the experimental data, except for the excitonic features near the band edge [48,49,50]. The calculated values of 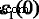 , which is called the static dielectric constant, for MoS2 multilayers and bulk can be found in Table 1. From Table 1, the calculated values of \( {\varepsilon}_1^{xx}(0) \) for multilayers and bulk MoS2 are all around 15.5, which is very close to the experimental value of 15.0 for bulk MoS2 [50]. The values of \( {\varepsilon}_1^{xx}(0) \) increase with the increasing number of MoS2 layers. For monolayer MoS2 , a clear peak B of \( {\varepsilon}_1^{xx}\left(\omega \right) \) appears about 2.54 eV. Peak B of monolayer is clearly more significant than multilayers, and they are all similar for multilayer MoS2 . As the layer number increases, the sharp structures (peak B) also move left slightly. In Fig. 6c, we also observe the emergence of long plateaus in the absorption coefficients, and absorption coefficients are around 1.5 × 10
5
cm
−1
at the long plateaus. There are also small steps around the thresholds for the absorption coefficients, which are consistent to those of the imaginary parts of dielectric function. With the layer number increases, the threshold energy of absorption coefficient decreases, while the number of small steps increases at the starting point of the plateau. For monolayer and multilayer MoS2 , strong absorption peaks emerge at visible light range (1.65–3.26 eV), and the monolayer MoS2 own a highest absorption coefficient of 1.3 × 10
6
cm
−1
. The theoretical absorption coefficients for different number of MoS2 layers are compared with confocal absorption spectral imaging of MoS2 (the inset) [46], as shown in Fig. 6c. For monolayer and multilayer MoS2 , a large peak of α (ω ) can be found at the position around 2.8 eV for both the calculation and experiment [46, 51]. Furthermore, a smoothly increase of α (ω ) can be found between 2.2 and 2.8 eV for both the theoretical and experimental curves. Therefore, from Fig. 6c, the calculated absorption coefficients of MoS2 multilayers show fairly good agreement with the experimental data [46], except for the excitonic peaks. The reflectivity spectra are given in Fig. 6d. The reflectivity spectra of MoS2 multilayers are all about 0.35–0.36 when energy is zero, which means that MoS2 system can reflect about 35 to 36% of the incident light. In the region of visible light, the maximum reflectivity of monolayer MoS2 is 64%, while the maxima of multilayer and bulk MoS2 are all about 58%. Because of the behaviors discussed, MoS2 monolayer and multilayers are being considered for photovoltaic applications.
, which is called the static dielectric constant, for MoS2 multilayers and bulk can be found in Table 1. From Table 1, the calculated values of \( {\varepsilon}_1^{xx}(0) \) for multilayers and bulk MoS2 are all around 15.5, which is very close to the experimental value of 15.0 for bulk MoS2 [50]. The values of \( {\varepsilon}_1^{xx}(0) \) increase with the increasing number of MoS2 layers. For monolayer MoS2 , a clear peak B of \( {\varepsilon}_1^{xx}\left(\omega \right) \) appears about 2.54 eV. Peak B of monolayer is clearly more significant than multilayers, and they are all similar for multilayer MoS2 . As the layer number increases, the sharp structures (peak B) also move left slightly. In Fig. 6c, we also observe the emergence of long plateaus in the absorption coefficients, and absorption coefficients are around 1.5 × 10
5
cm
−1
at the long plateaus. There are also small steps around the thresholds for the absorption coefficients, which are consistent to those of the imaginary parts of dielectric function. With the layer number increases, the threshold energy of absorption coefficient decreases, while the number of small steps increases at the starting point of the plateau. For monolayer and multilayer MoS2 , strong absorption peaks emerge at visible light range (1.65–3.26 eV), and the monolayer MoS2 own a highest absorption coefficient of 1.3 × 10
6
cm
−1
. The theoretical absorption coefficients for different number of MoS2 layers are compared with confocal absorption spectral imaging of MoS2 (the inset) [46], as shown in Fig. 6c. For monolayer and multilayer MoS2 , a large peak of α (ω ) can be found at the position around 2.8 eV for both the calculation and experiment [46, 51]. Furthermore, a smoothly increase of α (ω ) can be found between 2.2 and 2.8 eV for both the theoretical and experimental curves. Therefore, from Fig. 6c, the calculated absorption coefficients of MoS2 multilayers show fairly good agreement with the experimental data [46], except for the excitonic peaks. The reflectivity spectra are given in Fig. 6d. The reflectivity spectra of MoS2 multilayers are all about 0.35–0.36 when energy is zero, which means that MoS2 system can reflect about 35 to 36% of the incident light. In the region of visible light, the maximum reflectivity of monolayer MoS2 is 64%, while the maxima of multilayer and bulk MoS2 are all about 58%. Because of the behaviors discussed, MoS2 monolayer and multilayers are being considered for photovoltaic applications.
Conclusies
In this study, by employing ab initio calculations, the electronic and optical properties of MoS2 multilayers are investigated. Compared to bulk MoS2 , the covalency and ionicity of monolayer MoS2 are found to be stronger, which results from larger quantum confinement in the monolayer. With the increase of the layer number, quantum confinement and intra-layer interaction both decrease, meanwhile, the interlayer coupling increases, which result in the decrease of the band gap and the minimum direct energy gap. As the layer number becomes larger than two, the optical and electronic properties of MoS2 multilayers start to exhibit those of bulk. Band structures of multilayers and bulk show splitting of bands mainly around the Γ-point; however, splitting of bands in the vicinity of K point are tiny, owing to the small interlayer coupling at point K.
For optical properties, Van Hove singularities lead to the occurrence of long plateaus in both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \). At the beginnings of these long plateaus, monolayer, bilayer, and trilayer structures appear one, two, and three small steps, respectively. With the layer number increases, the number of small steps increases and the width of the small steps decreases, leading to unobvious steps. A small red shift in the threshold energy and a noticeable red shift in the end of both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateaus are observed, since the increased number of layers leads to small changes in the direct energy gap near point K (weak interlayer coupling) and larger changes near point Γ (stronger interlayer coupling). Thus, the longest plateau and shortest plateau of JDOS are from the monolayer and bulk, respectively. Our results demonstrate that the differences between electronic and optical properties for monolayer and multilayer MoS2 are significant; however, the differences are not obvious between the multilayer MoS2 . The present data can help understand the properties of different layers of MoS2 , which should be important for developing optoelectronic devices.
Beschikbaarheid van gegevens en materialen
The datasets supporting the conclusions of this article are included within the article.
Afkortingen
- Δ E:
-
The direct energy gap
- 1L:
-
Monolayer MoS2
- 2L:
-
Bilayer MoS2
- 3L:
-
Trilayer MoS2
- 4L:
-
Four-layer MoS2
- 5L:
-
Five-layer MoS2
- 6L:
-
Six-layer MoS2
- BSE:
-
Bethe-Salpeter equation
- BZ:
-
Brillouin zone
- CBM:
-
Minimaal geleidingsband
- GGA:
-
Gegeneraliseerde gradiëntbenadering
- GW:
-
Quasi-particle energy calculation
- JDOS:
-
Joint density of states
- MoS2 :
-
Molybdeendisulfide
- NC:
-
The ordinal numbers of conduction band
- NV:
-
The ordinal numbers of valence band
- PAW:
-
Projector augmented wave
- PBE:
-
Perdew-Burke-Ernzerhof
- VASP:
-
Wenen ab initio simulatiepakket
- VBM:
-
Maximale valentieband
- VHS:
-
Van Hove singularity
Nanomaterialen
- Onthulling van de atomaire en elektronische structuur van gestapelde koolstof nanovezels
- Structuur en elektronische eigenschappen van met overgangsmetaal gedoteerde kaoliniet nanoklei
- Modulatie van elektronische en optische anisotropie-eigenschappen van ML-GaS door verticaal elektrisch veld
- Eenvoudige synthese en optische eigenschappen van kleine selenium nanokristallen en nanostaafjes
- Effecten van dubbellaagse dikte op de morfologische, optische en elektrische eigenschappen van Al2O3/ZnO-nanolaminaten
- Optische en elektronische eigenschappen van door femtoseconde laser-geïnduceerde zwavel-hyperdoped silicium N+/P fotodiodes
- De structurele, elektronische en magnetische eigenschappen van Ag n V-clusters (n = 1–12) onderzoeken
- Afhankelijkheid van de toxiciteit van nanodeeltjes van hun fysische en chemische eigenschappen
- Optische eigenschappen van met Al-gedoteerde ZnO-films in het infraroodgebied en hun absorptietoepassingen
- Alkalimetaal-geadsorbeerde g-GaN-monolaag:ultralage werkfuncties en optische eigenschappen
- Elektronische eigenschappen van adsorptie van vanadiumatomen op schoon en met grafeen bedekt Cu(111)-oppervlak



