Efficiënte voorspelling en analyse van optische trapping op nanoschaal via eindige elementenscheur- en verbindingsmethode

Abstract

Numerieke simulatie speelt een belangrijke rol bij de voorspelling van optische trapping op basis van plasmonische nano-optische pincetten. Gecompliceerde structuren en drastische lokale veldversterking van plasmonische effecten brengen echter grote uitdagingen met zich mee voor traditionele numerieke methoden. In dit artikel wordt een nauwkeurige en efficiënte numerieke simulatiemethode voorgesteld op basis van een dual-oer eindige-elementen-scheuring en -verbinding (FETI-DP) en Maxwell-spanningstensor, om de optische kracht en het potentieel voor het vangen van nanodeeltjes te berekenen. Een low-rank sparsification-benadering wordt geïntroduceerd om de FETI-DP-simulatieprestaties verder te verbeteren. De voorgestelde methode kan een grootschalig en complex probleem ontleden in kleinschalige en eenvoudige problemen door gebruik te maken van niet-overlappende domeinverdeling en flexibele mesh-discretisatie, die een hoge efficiëntie en parallelliseerbaarheid vertoont. Numerieke resultaten tonen de effectiviteit aan van de voorgestelde methode voor de voorspelling en analyse van optische trapping op nanoschaal.

Inleiding

Plasmonische optische pincetten op basis van oppervlakteplasmonen (SP's) trekken veel aandacht en zijn op grote schaal toegepast om nanodeeltjes te vangen [1,2,3,4,5,6]. SP is een resonantiefenomeen dat wordt veroorzaakt door de koppeling van invallend licht met een specifieke golflengte en vrije elektronen op het grensvlak van de metalen en diëlektrica [7]. Met SP's kan het optische pincet de diffractielimiet doorbreken. Bovendien kan de drastische lokale veldverbetering van de SP's de vraag naar intensiteit van invallend licht verminderen [7, 8]. SP's zijn echter nauw verwant aan het materiaal en de afmetingen van objecten, evenals de golflengte van invallend licht, wat een groot aantal experimenten vereist om de optimale parameters van SP optische pincetten in de praktijk te bepalen. Op basis hiervan speelt de simulatiemethode een steeds belangrijkere rol als hulpmiddel bij het ontwerpen en optimaliseren van SP optische pincetten [9]. In deze simulaties is de berekening van optische kracht vereist om een stabiele trapping te voorspellen. Voor reguliere objecten zoals bollen kan de optische kracht analytisch worden afgeleid uit de algemene Lorenz-Mie-theorie [10, 11]. Voor objecten met gecompliceerde configuraties zijn echter numerieke methoden nodig die de heersende Maxwell-vergelijkingen rigoureus oplossen voor het modelleren van de elektromagnetische velden en de daaropvolgende optische kracht en potentiaal.

Deze numerieke methoden kunnen voornamelijk worden onderverdeeld in differentiaalvergelijkingsmethoden (DEM's) en integrale vergelijkingsmethoden (IEM's) [12,13,14,15]. Vergeleken met de IEM's laten differentiaalvergelijkingsmethoden (DEM's) superieure vaardigheden zien in het omgaan met gecompliceerde geometrieën en componenten. DEM's hebben ook het voordeel van een eenvoudige berekening van near-field distributie, die een belangrijke rol speelt bij de analyse van SP's. Als een representatieve DEM wordt de FDTD-methode (finite-difference time-domain) geïmplementeerd in het tijdsdomein, waarmee gemakkelijk breedbandinformatie en tijdelijke reacties kunnen worden verkregen [16, 17]. De FDTD vereist echter een nauwkeurig dispersief model om de frequentieafhankelijke materiaaleigenschappen in SP's te beschrijven, terwijl de nauwkeurigheid van de FDTD-oplossing sterk afhangt van de benaderingsnauwkeurigheid van dit dispersieve model [18]. Bovendien vertrouwt de FDTD op gestructureerde mazen, die vaak leiden tot trapfouten voor gebogen oppervlakken. Als een andere representatieve DEM is de eindige-elementenmethode (FEM) op grote schaal toegepast, omdat deze gemakkelijk dispersief materiaal in het frequentiedomein kan verwerken en de trapfout kan elimineren door ongestructureerde mesh [19,20,21,22]. Vergeleken met de FDTD kan de FEM direct gemeten materiaalparameters overnemen zonder enig benaderend dispersief model. Drastische lokale veldverbeteringen in de SP's vereisen echter fijne mazen in de FEM-discretisatie. Bovendien zullen objecten met grote afmetingen en meerdere objecten het aantal onbekenden drastisch verhogen. Deze factoren zullen leiden tot slecht geconditioneerde matrixsystemen en enorme rekenconsumpties, die grote uitdagingen met zich meebrengen voor traditionele FEM voor de analyse van SP-verbeterde optische trapping.

In dit artikel wordt een efficiënte dual-oer eindige-elementen-scheur- en verbindingsmethode (FETI-DP) geïntroduceerd om de optische trapping op nanoschaal te simuleren. De FETI-DP gebruikt een niet-overlappend domeindecompositieschema, dat een oorspronkelijk grootschalig complex probleem verdeelt in een reeks kleinschalige eenvoudige problemen om ze te overwinnen. Het dwingt een transmissievoorwaarde af op de subdomeininterfaces om de continuïteit van de ingediende bestanden te verzekeren, en introduceert een dubbele variabele om het oorspronkelijke driedimensionale (3D) probleem te reduceren tot een tweedimensionaal (2D) probleem door Lagrange-multiplier. Primaire variabelen in de subdomeinhoeken worden geëxtraheerd om de convergentiesnelheid van de iteratieve oplossing van het dubbele probleem te versnellen [23,24,25,26]. Er is een low-rank sparsification-benadering ontwikkeld om de prestaties van de FETI-DP te verbeteren. Het maakt gebruik van data-sparse-algoritmen om de efficiëntie te verbeteren voor het oplossen van de subdomeinproblemen en het dubbele probleem [27, 28]. De voorgestelde methode biedt volledig ontkoppelde subdomeinen, die de parallelle simulatie van optische kracht voor het vangen van nanodeeltjes mogelijk maken. De Maxwell-spanningstensor (MST) die de relatie tussen het elektromagnetische veld en het mechanische momentum onthult, wordt gebruikt om de optische kracht te evalueren [29]. Op basis van de verkregen optische kracht kan de optische potentiaal verder worden berekend voor de analyse van een stabiele trapping. Vergeleken met de IEM's is de voorgestelde methode krachtiger in het omgaan met samengestelde materialen en het oplossen van het nabije veld voor de op SP gebaseerde optische trapping. Vergeleken met de FDTD kan de voorgestelde methode nauwkeurig dispersief metaalmateriaal verwerken in de op SP gebaseerde optische vangsystemen en de trapfout elimineren voor de objecten met curvegrens. Vergeleken met de FEM is de voorgestelde methode geschikt voor grootschalige berekening van optische trapping. Verschillende voorbeelden worden geanalyseerd en numerieke resultaten demonstreren de nauwkeurigheid en efficiëntie van de voorgestelde methode voor de voorspelling en analyse van optische trapping op nanoschaal.

Methoden

FETI-DP-formuleringen

Voor de FETI-DP-implementatie wordt het oorspronkelijke rekendomein Ω eerst gescheurd in een reeks niet-overlappende subdomeinen Ωⁱ (ik = 1, 2, 3⋯, N _s ), zoals weergegeven in Fig. 1. In elk subdomein Ωⁱ , kan een subdomein eindige elementensysteem worden afgeleid uit de vectorgolfvergelijking als

$$ \nabla \times {\mu}_r^{-1}\nabla \times {\mathbf{E}}^i-{k}_0^2{\varepsilon}_r{\mathbf{E}}^i ={jk}_0{\eta}_0{\mathbf{J}}_{\mathrm{imp}}^i\kern1.08em \mathrm{in}\kern0.24em {\Omega}^i $$ (1 ) $$ \hat{n}\times \nabla \times {\mathbf{E}}^i+{jk}_0\hat{n}\times \left(\hat{n}\times {\mathbf{E} }^i\right)=0\kern0.96em \mathrm{on}\kern0.24em {\Gamma}_{\mathrm{ABC}}^i $$ (2)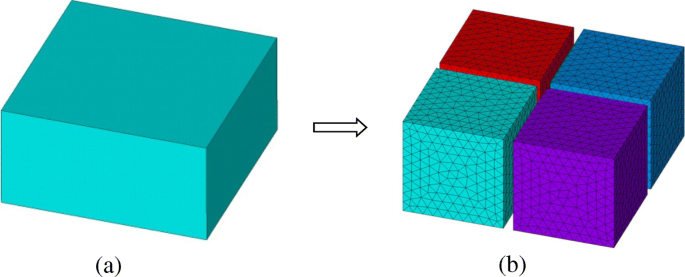

Een domeinverdelingsschema met niet-overlappende subdomeinen in de FETI-DP-methode. een Origineel domein. b Verdeelde subdomeinen en gediscretiseerde meshes

waar E ^ik geeft het onbekende elektrische veld aan dat moet worden opgelost in $ {\Omega}^i $, k ₀ en η ₀ zijn respectievelijk het vrije-ruimtegolfgetal en de intrinsieke impedantie, en $ {\mathbf{J}}_i^{\mathrm{imp}} $ is de opgedrukte stroom. $ {\Gamma}_{\mathrm{ABC}}^i $ betekent de absorberende randvoorwaarde (ABC) om het oneindige open gebied af te kappen. Opgemerkt moet worden dat k ₀ moet worden vervangen door de golfimpedantie in het medium als het omringende medium geen vrije ruimte is, wat gebruikelijk is voor optische trapping. Op de subdomeininterface Γⁱ , is een veronderstelde randvoorwaarde vereist om een volledig randwaardeprobleem te genereren in Ωⁱ . Hier een transmissieconditie van het Robin-type met een onbekende hulpvariabele Λ _ik wordt opgelegd als

$$ {\hat{n}}^i\times \left({\mu}_r^{-1}\nabla \times {\mathbf{E}}^i\right)+{\alpha}^i{ \hat{n}}^i\times \left({\hat{n}}^i\times {\mathbf{E}}^i\right)={\boldsymbol{\Lambda}}^i\kern1. 2em \mathrm{op}\kern0.36em {\Gamma}^i $$ (3)

waarbij $ {\hat{n}}^i $ de eenheidsnormaal uitgaande vector op de subdomeininterface aangeeft Γⁱ , en α ^ik is een complexe parameter die vaak kan worden gekozen als jk ₀ . Alle subdomeinen worden vervolgens gediscretiseerd door tetraëdrische elementen. In elk element breiden we E . uit met vectorbasisfuncties N en onbekende elektrische veldcoëfficiënt E als

$$ \mathbf{E}=\sum \limits_{p=1}^s{E}_p{\mathbf{N}}_p $$ (4)

waar s geeft het aantal vectorbasisfuncties in elk tetraëdrisch element aan. s is gekozen als 6 voor traditionele basisfuncties van lage orde op basis van de rand, terwijl het groter is voor vectorbasisfuncties van hoge orde, aangezien aanvullende basisfuncties op basis van vlak of volume worden geïntroduceerd.

Toepassing van Galerkin's methode, de FEM-matrixvergelijking in Ωⁱ over de onbekende elektrische veldcoëfficiënt E ^ik kan worden verkregen als

$$ \left(\begin{array}{cc}{\mathbf{K}}_{rr}^i&{\mathbf{K}}_{rc}^i\\ {}{\mathbf{K}} _{cr}^i&{\mathbf{K}}_{cc}^i\end{array}\right)\left(\begin{array}{l}{E}_r^i\\ {}{E }_c^i\end{array}\right)=\left(\begin{array}{l}{f}_r^i-{\mathbf{B}}_r^{i^T}{\lambda}^ i\\ {}{f}_c^i\end{array}\right) $$ (5)

waarbij de subscript-notaties c en r onderscheid de hoekgraden van vrijheid (DOF's) en de resterende DOF's, die de hoek-DOF's extraheert als een oervariabele om het dual-oer (DP) -schema te construeren. Hier, K is de FEM-systeemmatrix en f is de excitatievector. B is een Booleaanse matrix die de interface-DOF's van een subdomein extraheert. λ is een dubbele variabele die wordt gegenereerd door het uitbreiden van Λ _ik , ook wel de Lagrange-multiplier genoemd.

Vervolgens kunnen de aangrenzende subdomeinen met elkaar worden verbonden door de continuïteit van tangentieel elektrisch veld en magnetisch veld op de interfaces af te dwingen. We assembleren alle subdomeininterfaces en elimineren alle interne onbekenden van het subdomein E ^ik . Een gereduceerde globale interfacevergelijking over de dubbele variabele λ kan worden verkregen als

$$ \left[{\tilde{\mathbf{K}}}_{rr}+{\tilde{\mathbf{K}}}_{rc}{\tilde{\mathbf{K}}}_{cc }^{-1}{\tilde{\mathbf{K}}}_{cr}\right]\lambda ={\tilde{f}}_r-{\tilde{\mathbf{K}}}_{rc }{\tilde{\mathbf{K}}}_{cc}^{-1}{\tilde{f}}_c $$ (6)

Vergelijking (6) kan worden opgelost door iteratieve methoden, zoals de gegeneraliseerde minimale residuele (GMRES) methode. $ {\tilde{\mathbf{K}}}_{cc} $ is het globale hoeksysteem, dat de iteratieve convergentie in de oerruimte kan versnellen. Geschikte preconditioner kan worden gebruikt om de iteratieve convergentiesnelheid te verbeteren, zoals bij benadering inverse en onvolledige LU-ontleding. Zodra de dubbele variabele λ is opgelost, kan het elektrische veld binnen elk subdomein onafhankelijk worden geëvalueerd door (5). Voor de constructie van de globale matrix $ {\tilde{\mathbf{K}}}_{rr} $, moet men de subdomein numerieke functie Green's functie $ {\mathbf{Z}}_{rr}^ construeren i $ met een vorm van

$$ {\mathbf{Z}}_{rr}^i={\mathbf{B}}_r^i{\left({\mathbf{K}}_{rr}^i\right)}^{- 1}{{\mathbf{B}}_r^i}^T $$ (7)

waarbij de inverse van de subdomein FEM-matrix $ {\left({\mathbf{K}}_{rr}^i\right)}^{-1} $ is opgenomen. Trouwens, voor matrices $ {\tilde{\mathbf{K}}}_{rc} $, $ {\tilde{\mathbf{K}}}_{cr} $, en $ {\tilde {\mathbf{K}}}_{cc} $ en vectoren $ {\tilde{f}}_r $ en $ {\tilde{f}}_c $, de $ {\left({ \mathbf{K}}_{rr}^i\right)}^{-1} $ moet worden berekend. De constructies van $ {\left({\mathbf{K}}_{rr}^i\right)}^{-1} $ in de pre-processing fase evenals hun matrix-vector producten (MVP's) bij iteratieve oplossingsfase zijn rekenkundig duur. Hoewel $ {\mathbf{K}}_{rr}^i $ schaars is, $ {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \ ) zijn compact, wat hoge rekenkosten betekent. Vervolgens wordt een low-rank sparsificatiemethode geïntroduceerd om de berekening van \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} $ te versnellen. Aangezien sommige submatrices in het globale interfacesysteem kunnen worden weergegeven in matrixvorm met een lage rangorde, kan hun berekening worden uitgevoerd met een laagrangalgoritme, wat de prestaties van de FETI-DP verbetert. Het is te zien dat de FETI-DP onafhankelijke subdomeinbewerkingen biedt, zodat deze parallelle berekening kan gebruiken om de efficiëntie te verbeteren. Voor een efficiënt parallel schema is een principe van domeinverdeling om het aantal DOF's in elk subdomein zo evenwichtig mogelijk te maken. Daarom moet de grootte van subdomeinen betrekking hebben op de mesh-discretisatiedichtheid. Gewoonlijk worden kleine subdomeinen gebruikt in fijnmazige gebieden, terwijl grote subdomeinen worden gebruikt in grofmazige gebieden.

Lage sparsificatie

Er wordt een low-rank sparsification-benadering voorgesteld om een data-arme manier te bieden om de FETI-DP-efficiëntie te verbeteren. Hier, data-sparse betekent dat deze matrices eigenlijk niet schaars zijn, maar dat ze schaars zijn in de zin dat bepaalde subblokken ervan kunnen worden weergegeven door laagwaardige ontledingsmatrixvormen als

$$ \mathbf{M}={\mathbf{XY}}^{\mathrm{T}}\kern0.72em \left(\mathbf{M}\in {\mathrm{\mathbb{C}}}^{ m\times n},\mathbf{X}\in {\mathrm{\mathbb{C}}}^{m\times k},\mathbf{Y}\in {\mathrm{\mathbb{C}}} ^{n\times k}\right) $$ (8)

waar X en J zijn in volledige matrixvormen, en de rang k is veel kleiner dan m en n . De matrix $ {\left({\mathbf{K}}_{rr}^i\right)}^{-1} $ kan worden weergegeven door data-sparse matrixvormen omdat deze de matrixeigenschap van een integraal bezit exploitant. Dus, op voorwaarde dat $ {\left({\mathbf{K}}_{rr}^i\right)}^{-1} $ een eigenschap van lage rang heeft in een bepaald subdomein, kan het efficiënt worden berekend en opgeslagen in data-sparse vormen met de low-rank sparsification-aanpak, die de MVP's in de iteratieve oplossing versnelt.

De processen van de low-rank sparsification-benadering kunnen worden onderverdeeld in de volgende stappen:(1) construeer een clusterboom door de basisfunctieset in elk subdomein onder te verdelen, (2) construeer een blokclusterboom door interactie van twee clusterbomen, ( 3) genereer een data-sparse vorm van $ {\mathbf{K}}_{rr}^i $ door een toelaatbaarheidsvoorwaarde, (4) voer low-rank geformatteerde algoritmen uit om de data-sparse representatie van $ {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}^{-1} $, en (5) voer de oplossing van FETI-DP-systemen in door data-sparse algoritme. Geschikte preconditioner kan worden gebruikt om de oplossing te versnellen. Opgemerkt moet worden dat de data-sparse LU-factorisatie $ {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}={\left({\mathbf {L}}_{rr}^i\right)}_{\mathrm{DS}}{\left({\mathbf{U}}_{rr}^i\right)}_{\mathrm{DS} } $ wordt gebruikt om de matrixinversie $ {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}^{-1} $ te vervangen. Een geneste dissectietechniek wordt gebruikt om de efficiëntie van de lage sparsificatie verder te verbeteren. De geneste dissectie gebruikt scheidingstekens om grote off-diagonale nul-subblokken op te leveren, die nul zullen blijven tijdens de LU-factorisatie, zodat het de fill-ins aanzienlijk kan verminderen.

Om \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}} \ te genereren, construeren we eerst een clusterboom T _Ik door recursieve onderverdeling van de subdomein edge-gebaseerde basisfunctieset I = {1,2,……N } met behulp van een selectiekader. Met de geneste dissectie, een cluster t binnen het bijbehorende selectiekader is verdeeld in drie opvolgers {s ₁ , s _september , s ₂ }, waar s ₁ en s ₂ zijn de indexsets van de twee niet-verbonden begrenzingsvakken en s _september is de indexset van het scheidingsteken. Figuur 2a toont een eenvoudig voorbeeld van dit proces. Vervolgens een blokclusterboom T _{Ik × Ik} kan worden geconstrueerd door interactie met twee clusterbomen T _Ik , zoals getoond in Fig. 2b, die kan worden gekozen als de clusterboom van de originele op randen gebaseerde basisfunctiesset en die van de testbasisfunctieset in de methode van Galerkin. Vervolgens moeten we een toelaatbaarheidsvoorwaarde introduceren op basis van de geneste dissectie om onderscheid te maken tussen volledige blokken, lage decompositieblokken en niet-diagonale nulblokken in T _{Ik × Ik} [23]. Dus, $ {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}} $ kan worden geproduceerd door de corresponderende blokken te vullen met de niet-nul items van $ {\mathbf{K}}_{rr}^i $. Ten slotte de data-sparse LU-factorisatie van \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}={\left({\mathbf{L }}_{rr}^i\right)}_{\mathrm{DS}}{\left({\mathbf{U}}_{rr}^i\right)}_{\mathrm{DS}} \ ) kan recursief worden berekend uit

$$ {\mathbf{K}}_{rr}^i=\left[\begin{array}{ccc}{\mathbf{K}}_{11}&&{\mathbf{K}}_{13 }\\ {}&{\mathbf{K}}_{22}&{\mathbf{K}}_{23}\\ {}{\mathbf{K}}_{31}&{\mathbf{K }}_{32}&{\mathbf{K}}_{33}\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{L}}_{11}&&\\ {}&{\mathbf{L}}_{22}&\\ {}{\mathbf{L}}_{31}&{\mathbf{L}}_{32}&{\mathbf{ L}}_{33}\end{array}\right]\left[\begin{array}{ccc}{\mathbf{U}}_{11}&&{\mathbf{U}}_{13} \\ {}&{\mathbf{U}}_{22}&{\mathbf{U}}_{23}\\ {}&&{\mathbf{U}}_{33}\end{array} \right] $$ (9)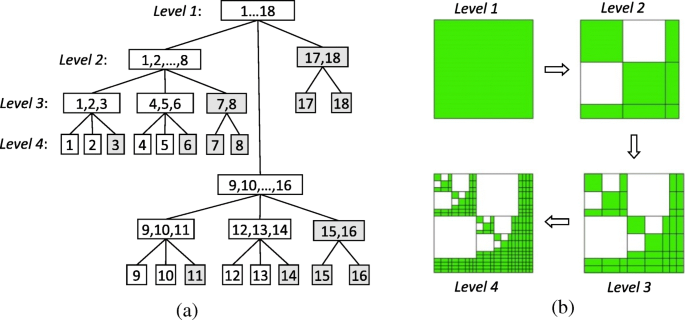

Constructies van een clusterboom en een blokclusterboom van 4 niveaus op basis van geneste dissectie. een Constructie van een clusterboom door recursieve onderverdeling van op edge gebaseerde basisfunctieset I = {1,2,…18}. b Constructie van een blokclusterboom waar wit blokken zijn nulmatrices en groen blokken kunnen volledige matrices of lage decompositiematrices zijn

waar conventionele volledige matrixberekeningen worden vervangen door hun tegenhangers met weinig gegevens [28]. Een adaptieve afbreekfout ε _t wordt gebruikt om de nauwkeurigheid van lage-rang benaderingen te controleren. De verkregen LU-factoren $ {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}} $ en $ {\left({\mathbf{U}) }_{rr}^i\right)}_{\mathrm{DS}} $ worden opgeslagen en gebruikt om $ {\mathbf{Z}}_{rr}^i $ te construeren door

$$ {\mathbf{Z}}_{rr}^i={\mathbf{B}}_r^i{\left({\mathbf{U}}_{rr}^i\right)}_{\ mathrm{DS}}^{-1}{\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}}^{-1}{\mathbf{B} }_r^i $$ (10)

waarbij $ {\mathbf{B}}_r^i{\left({\mathbf{U}}_{rr}^i\right)}_{\mathrm{DS}}^{-1} $ en $ {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}}^{-1}{\mathbf{B}}_r^i $ kan berekend door data-sparse bovenste en onderste driehoekige solver. De $ {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}} $, $ {\left({\mathbf{U}}_{ rr}^i\right)}_{\mathrm{DS}} $, en $ {\mathbf{Z}}_{rr}^i $ voer de FETI-DP-berekening in met data-sparse vooruit en achteruit substituties (FBS's) en data-sparse MVP's.

Optische kracht en potentieel

Volgens de elektrodynamische theorie kan de optische kracht worden geëvalueerd door de Maxwell-spanningstensor (MST) die de relatie tussen elektromagnetisch veld en mechanisch momentum onthult [29]. Zodra de elektromagnetische veldverdeling rond het object is verkregen, kan de optische kracht worden berekend door MST te integreren over een gesloten oppervlak dat het object omringt. Op basis van de verkregen elektrische veldverdeling kan de MST op elke coördinaten worden geconstrueerd door

$$ \overleftrightarrow{\mathbf{T}}=\frac{1}{2}\operatorname{Re}\left[\varepsilon {\mathbf{EE}}^{\ast }+\mu {\mathbf{HH }}^{\ast }-\frac{1}{2}\left(\varepsilon {\left|\mathbf{E}\right|}^2+\mu {\left|\mathbf{H}\right |}^2\right)\overleftrightarrow{\mathbf{I}}\right] $$ (11)

waarbij het sterretje in superscript het geconjugeerde elektrisch veld of magnetisch veld aangeeft, ε zijn μ zijn de permittiviteit en permeabiliteit, en $ \overleftrightarrow{\mathbf{I}} $ is een 3 × 3 identiteitsmatrix. Door het uitwendige product van vectoren kan de tensorvorm van $ \overleftrightarrow{\mathbf{T}} $ worden geschreven als

$$ \overleftrightarrow{\mathrm{T}}=\left[\begin{array}{lll}{T}_{xx}&{T}_{xy}&{T}_{xz}\\ {} {T}_{yx}&{T}_{yy}&{T}_{yz}\\ {}{T}_{zx}&{T}_{zy}&{T}_{zz} \end{array}\right]=\left[\begin{array}{ccc}\varepsilon {E}_x{E}_x^{\ast }+\mu {H}_x{H}_x^{\ast }-\frac{\varepsilon {\left|\mathbf{E}\right|}^2+\mu {\left|\mathbf{H}\right|}^2}{2}&\varepsilon {E} _x{E}_y^{\ast }+\mu {H}_x{H}_y^{\ast }&\varepsilon {E}_x{E}_z^{\ast }+\mu {H}_x{ H}_z^{\ast}\\ {}\varepsilon {E}_y{E}_x^{\ast }+\mu {H}_y{H}_x^{\ast }&\varepsilon {E}_y {E}_y^{\ast }+\mu {H}_y{H}_y^{\ast }-\frac{\varepsilon {\left|\mathbf{E}\right|}^2+\mu { \left|\mathbf{H}\right|}^2}{2}&\varepsilon {E}_y{E}_z^{\ast }+\mu {H}_y{H}_z^{\ast} \\ {}\varepsilon {E}_z{E}_x^{\ast }+\mu {H}_z{H}_x^{\ast }&\varepsilon {E}_z{E}_y^{\ast }+\mu {H}_z{H}_y^{\ast }&\varepsilon {E}_z{E}_z^{\ast }+\mu {H}_z{H}_z^{\ast }- \frac{\varepsilon {\left|\mathbf{E}\right|}^2+\mu {\left|\mathbf{H}\right|}^2}{2}\end{array}\right] $$ (12)

waarbij het subscript x , j , z geeft de componenten in drie richtingen aan. Volgens de uitbreiding van E beschreven in (4), de vermeldingen van MST T _mn (m , n = x , j , z ) kan worden omgezet in uitgebreide vormen in de FETI-DP-berekening als

$$ {\displaystyle \begin{array}{l}{T}_{mn}=\sum \limits_{p,q=1}^s{E}_p{E}_q\left\{\varepsilon {\ left({\mathbf{N}}_p\right)}_m{\left({\mathbf{N}}_q^{\ast}\right)}_n-\frac{1}{\omega^2\mu }{\left(\nabla \times {\mathbf{N}}_p\right)}_m{\left(\nabla \times {\mathbf{N}}_q^{\ast}\right)}_n\right .\\ {}\kern1.75em \left.-\frac{1}{2}\left[\varepsilon \left({\mathbf{N}}_p\right)\left({\mathbf{N}} _q^{\ast}\right)-\frac{1}{\omega^2\mu}\left(\nabla \times {\mathbf{N}}_p\right)\left(\nabla \times {\ mathbf{N}}_q^{\ast}\right)\right]\right\}\kern1.75em \mathrm{if}\ m=n.\end{array}} $$ (13) $$ {T }_{mn}=\sum \limits_{p,q=1}^s{E}_p{E}_q\left\{\varepsilon {\left({\mathbf{N}}_p\right)}_m {\left({\mathbf{N}}_q^{\ast}\right)}_n-\frac{1}{\omega^2\mu }{\left(\nabla \times {\mathbf{N} }_p\right)}_m{\left(\nabla \times {\mathbf{N}}_q^{\ast}\right)}_n\right\}\kern1.25em \mathrm{if}\ m\ne N. $$ (14)

waar ω is de hoekfrequentie; N en s zijn beschreven in vgl. (4).

Ten slotte kan de optische kracht die op het object wordt uitgeoefend worden berekend door de MST te integreren over een gesloten oppervlak eromheen door

$$ \mathbf{F}={\oint}_S\left(\overleftrightarrow{\mathbf{T}}\cdot \hat{n}\right)\ dS. $$ (15)

Merk op dat de berekening van optische kracht ook parallel kan worden uitgevoerd, aangezien de integraal van de MST wordt toegewezen aan overeenkomstige subdomeinen. Voor een stabiele optische trapping is een van de belangrijkste voorwaarden dat de gradiëntkracht groter moet zijn dan de verstrooiingskracht. Met andere woorden, de richting van de totale kracht moet identiek zijn aan die van de gradiëntkracht, die altijd wijst naar de positie waar de elektrische veldintensiteit het sterkst is.

Het optische potentieel is een andere aantrekkelijke parameter die de stabiliteit van de optische trapping onthult. Gebaseerd op de verkregen optische kracht, de optische potentiaaldiepte U op positie r ₀ kan worden berekend door

$$ \mathbf{U}\left({r}_0\right)=-{\int}_{\infty}^{r_0}\mathbf{F}\left(\mathbf{r}\right)\cdot \mathbf{r}, $$ (16)

waarbij het subscript ∞ oneindigheid aangeeft, gedefinieerd als het referentiepunt met nulpotentiaal. De waarde van U kan worden weergegeven door k _B T, waar k _B geeft de Boltzmann-constante aan van 1,3806488 × 10⁻²³ J/K en T is de omgevingstemperatuur. Over het algemeen kan het deeltje de Brownse beweging in oplossing overwinnen en stabiel worden gevangen wanneer U> 1 k _B T is tevreden. Anders kan het deeltje niet stabiel worden opgesloten. Aangezien de totale optische kracht de conservatieve gradiëntkrachtcomponent en de niet-conservatieve verstrooiingskrachtcomponent omvat, is de totale optische kracht F van (15) is niet-conservatief [30, 31]. Als de beweging van het nanodeeltje echter beperkt blijft tot één dimensie, levert dit een eenduidige definitie op van een optische potentiaal uit (16), ook al is de totale optische kracht niet-conservatief.

Resultaten en discussie

Er worden drie voorbeelden gegeven om de effectiviteit van de voorgestelde methode aan te tonen. Omdat edelmetalen vaak worden gebruikt om het oppervlakteplasmon te prikkelen, selecteren we representatieve goud- en zilvermaterialen voor de analyses. Het eerste voorbeeld berekent de optische kracht van zilveren nanodeeltjes om de nauwkeurigheid van de voorgestelde methode te verifiëren. Het tweede en derde voorbeeld simuleren en bespreken de optische trapping van gouden nanodeeltjes. Voor alle voorbeelden wordt het oneindige domein afgekapt met ABC, en de afstanden tussen het ABC en de objecten zijn ingesteld op één golflengte, wat voldoende is om een acceptabele nauwkeurigheid te bereiken. Alle berekeningen worden uitgevoerd op een Dell-werkstation dat is uitgerust met 3,6 GHz Intel Xeon-processors.

Zilveren nanocapsule

Een zilveren nanocapsule-object wordt eerst overwogen om de nauwkeurigheid en efficiëntie van de voorgestelde FETI-DP-methode bij het voorspellen van optische kracht te testen. Figuur 3 a en b geven de configuratie en afmetingen weer. De constitutieve parameters van zilver zijn allemaal gemeten waarden uit [32]. Om het FETI-DP-schema te implementeren, wordt het hele analysedomein eerst verdeeld in 24 subdomeinen. Dichtere mazen zijn nodig in de buurt van het metalen oppervlak om het plasmonische lokale veldversterkingseffect te modelleren. Tetraëdrische elementen worden gebruikt voor de discretisatie, wat leidt tot een totaal van 6,9 × 10⁵ onbekenden, waaronder 4,1 × 10⁴ dubbele onbekenden en 313 hoek onbekenden. Het invallende licht brandt in de richting van +z , terwijl de polarisatierichting van het elektrische veld −x . is .

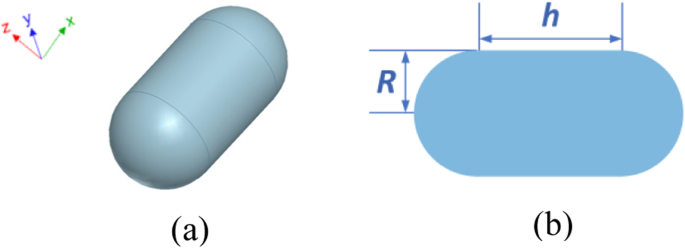
Configuratie van een zilveren nanocapsulestructuur. een 3D-weergave. b Vooraanzicht en afmetingen, waar R = 30 nm en h = 60 nm

Eerst veranderen we de golflengte van invallend licht λ van 200 nm tot 400 nm om de optische krachten te simuleren die op de nanocapsule worden uitgeoefend. Omdat de FETI-DP in het frequentiedomein werkt, worden de optische krachten berekend op 15 bemonsteringsfrequentiepunten. Figuur 4 toont de berekende curve van optische krachten die op de zilveren nanocapsule worden uitgeoefend. Om de nauwkeurigheid van de FETI-DP aan te geven, worden de resultaten van de optische kracht van de FETI-DP vergeleken met die van de commerciële software Lumerical FDTD Solutions [33], en er kan een goede overeenkomst worden waargenomen.

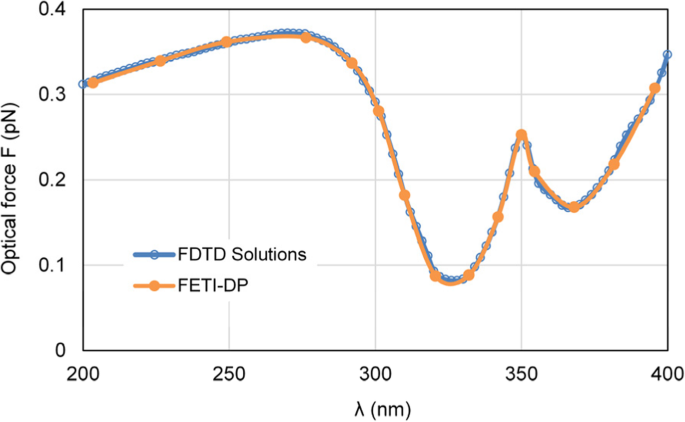
Resultaten van de optische krachten uitgeoefend op de zilveren nanocapsule, variërend met de golflengte λ of incident light, including the results of the FETI-DP and the commercial software FDTD solutions

Then, the performance of FETI-DP is tested for different numbers of subdomains. We increase the number of subdomains from 4 to 24 by keeping the discretization density. We assign each processor to deal with one subdomain. Table 1 reports the time used for the construction of global interface Eq. (6) and the total solution time. It can be seen that the FETI-DP can fully exploit parallel computing resources and significantly improve the solution efficiency. Besides, the accuracy of the FETI-DP with the number of subdomains increasing is also examined and reported in Table 1. Here, the accuracy is defined by the 2-norm relative error of the optical force as δ _OF = ‖OF _ik − OF _ref ‖/‖OF _ref ‖, where OF _ik is the optical force using i subdomains and OF _ref denotes the reference optical force using two subdomains. It can be seen that the accuracy keeps almost constant with the number of subdomains increasing.

Gold Nanosphere Dimer

The second example analyzes the optical trapping of a gold nanosphere by using a gold nanosphere dimer. The plasmonic effects at the dimer gap can effectively enhance the optical force for trapping nanoparticle. Figure 5 a and b gives the configuration and dimensions of this system. The constitutive parameters of gold are all measured values taken from [32]. The surrounding medium is water with a relative refractive index of n = 1.33. The incident light is a plane wave with the power of 10 mW/μm² , the electric field polarization direction is +x , and the incident direction is −z . The optical force exerted on the object nanosphere is calculated by the FETI-DP method. For the FETI-DP implementation, the whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which results in 3.5 × 10⁶ unknowns, including 1.6 × 10⁵ dual unknowns and 1738 corner unknowns.

Configuration of an optical trapping system of a gold nansphere dimer in water. een 3D view. b Front view and dimensions, where R = 25 nm, r = 5 nm, and g = 2 nm

First, we test the parallel performance of the proposed FETI-DP by using various numbers of processors. Table 2 reports the solution time for Eq. (6) as well as the total solution time. Besides, the speedups for the parallel computation are also provided in Table 2. Here, the speedup is defined by

$$ \mathrm{Speed}\ \mathrm{up}=\raisebox{1ex}{${T}_1$}\!\left/ \!\raisebox{-1ex}{${T}_{N_p}$}\right. $$ (17)

where $ {T}_{N_p} $ denotes the total wall-clock time using N _p processors. It can be seen that the FETI-DP significantly improves the solution efficiency and exhibits good parallel speedup. For this large number of unknowns, the total memory usage of all the processors is only 57.2 GB.

Then, the effectiveness of the low-rank sparsification approach is examined. With the low-rank sparsification, the subdomain matrix can be factorized by data-sparse algorithm and stored as data-sparse matrices. The construction time and memory usage are only 18 s and 0.5 GB, while they are 67 s and 1.7 GB by conventional matrix algorithm. It can be seen that we get 72% time saving and 70% memory compression. Related to the memory usage, the subsequent MVPs can also get 70% time-saving.

Next, the FETI-DP is tested for the optical force calculation with the wavelength λ varying from 277 nm to 818 nm. In practice, the analyses of optical force under incident light of different wavelengths are often necessary for searching the plasmonic resonance wavelength, where drastic field enhancement occurs and the strongest optical force can be obtained. Two cases are considered with the nanosphere located at (0, 0, 20 nm) and (0, 0, − 20 nm). Figure 6 a and b plots the calculated optical forces exerted on the nanosphere for different λ . It can be seen that the maximum optical force occurs at λ = 472 nm, which is the plasmonic resonance wavelength. The optical force at this resonance wavelength enhanced by nearly 40 times as against that at non-resonance wavelength. Moreover, the optical force always points to the dimer gap, as shown in Fig. 6, where the electric field intensity is strongest. It is also the direction of gradient force to trap the object. Figure 7 a and b shows the calculated electric field enhancement distributions at the non-resonance wavelength of λ = 300 nm and the resonance wavelength of λ = 472 nm, respectively. It can be seen that the electric field intensity has been increased by almost 250 times due to the plasmonic resonance effect.

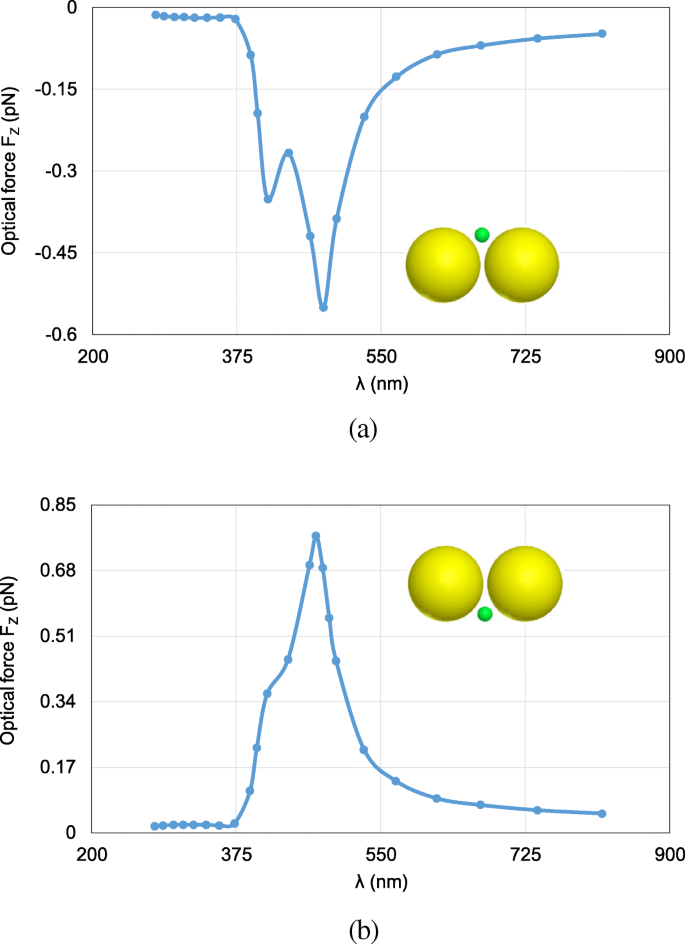
Calculated results of optical forces exerted on the nanosphere in the system of gold nanosphere dimer, varying with the wavelength λ of incident light. een The object nanosphere is located at (0, 0, 20 nm). b The object nanosphere is located at (0, 0, − 20 nm)

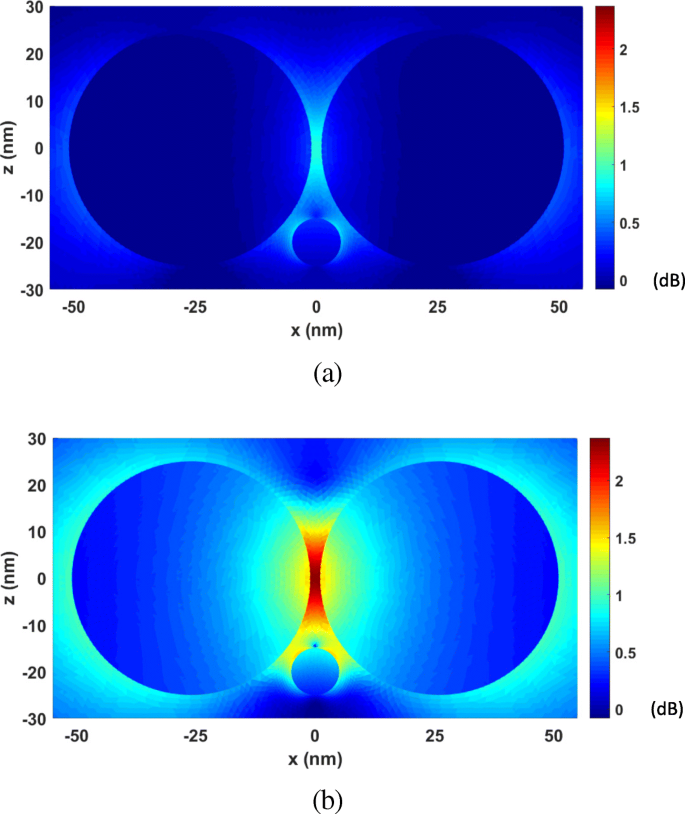
The electric field enhancement distributions on the xoz plane for the system of gold nanosphere dimer. een λ = 300 nm (non-resonance wavelength). b λ = 472 nm (resonance wavelength)

Besides, the optical force and optical potential are calculated with the nanosphere moving from (0, 0, − 30 nm) to (0, 0, − 17 nm) along the z -as. Since the most typical and interesting behavior of trapping forces and potentials are those acting along z -direction, we here consider the axial trapping potential by integration along the z -as. Because the motion of the nanoparticle is restricted to one dimension, the definition of an optical potential is unambiguous from (16), even though the total optical force from (15) is non-conservative. As shown in Fig. 8 a, b, with the nanosphere moving to the dimer gap, the optical force and optical potential depth obviously increase. At the position of (0, 0, − 17 nm), an optical potential depth of 4.6 k _B T is produced, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

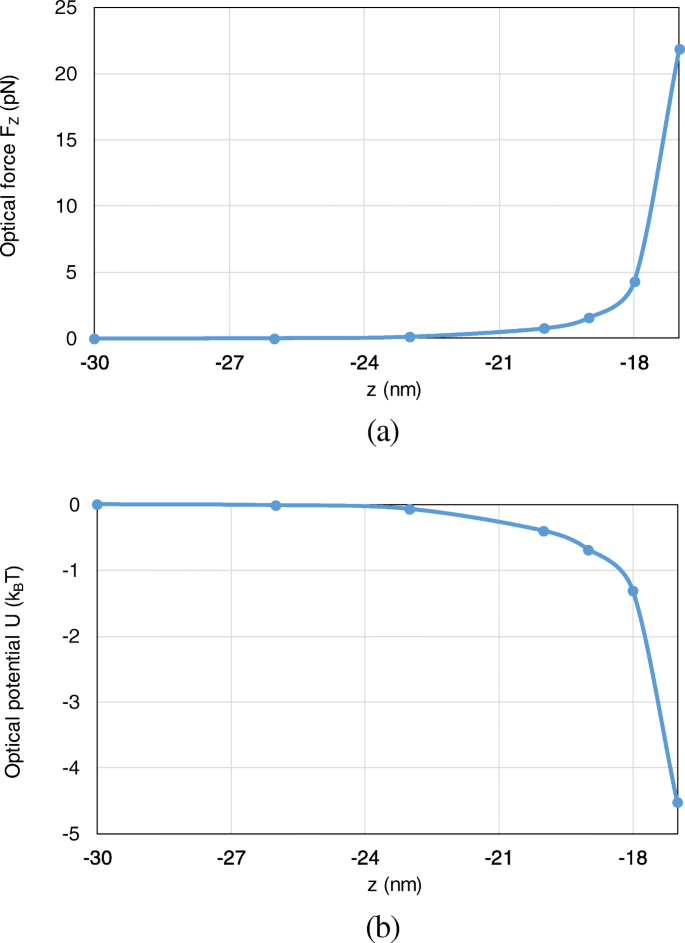
The optical forces and optical potentials exerted on the nanosphere in the system of gold nanosphere dimer, when the nanosphere moves from (0, 0, − 30 nm) to (0, 0, − 17 nm). een The optical forces. b The optical potentials

Finally, we test the effects of the dielectric substrate for this example. The optical forces are calculated with and without a substrate, respectively. For both two cases, the nanosphere is located at (0, 0, − 20 nm) and the incident wavelength is chosen as the resonance wavelength. For the case without substrate, the calculated result of the optical force is |F ₀ | = 0.769 pN. For the case with a substrate, the gold nanosphere dimer is put on a dielectric substrate with a thickness of 60 nm and a relative permittivity of ε _r = 2.25. The calculated result of the optical force is |F ₁ | = 0.761 pN. The relative error between these two results of optical forces is about 1.0 × 10⁻² , which is defined as |F ₁ − F ₀ |/|F ₀ |.

Gold Truncated Cone Dimer

The third example deals with the optical trapping of a gold nanosphere by using a gold truncated cone dimer. Figure 9 gives the configuration and dimensions of this system. The constitutive parameters of gold are taken from [32]. The dielectric substrate has a relative permittivity of ε _r = 2.25. The surrounding medium is water with a relative refractive index of n = 1.33. The incident light is plane wave with the power of 10 mW/μm² , the electric field polarization direction is +x , and the incident direction is −z . The whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which leads to 3.1 × 10⁶ unknowns, including 1.3 × 10⁵ dual unknowns and 1227 corner unknowns.

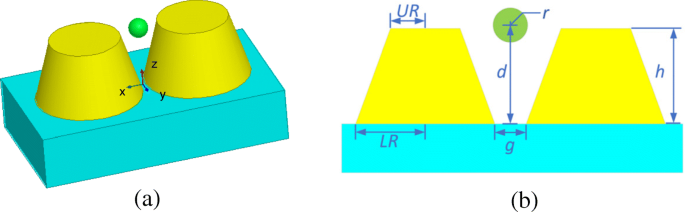
Configuration of an optical trapping system of a gold truncated cone dimer based on a dielectric substrate in water. een 3D view. b Front view and dimensions, where UR = 20 nm, LR = 30 nm, h = 35 nm, and g = 2 nm

First, we analyze the optical forces by changing λ from 277 nm to 818 nm. Figure 10 plots the calculated optical forces exerted on the nanosphere for different λ . The nanosphere is located at (0, 0, 35 nm). It can be seen that the maximum optical force occurs at λ = 464 nm, which is the plasmonic resonance wavelength, and the optical force here is enhanced by nearly 30 times at non-resonance wavelength. Moreover, the total optical force always points to −z , as shown in Fig. 10, which is the direction of the gradient force. This confirms that the gradient force is greater than the scattering force, which is one of the conditions that the nanosphere can be stably trapped. Figure 11 a and b presents the calculated electric field distributions at the non-resonance wavelength of λ =300 nm and the resonance wavelength of λ = 464 nm, respectively. It can be seen that electric field intensity has been increased by almost 500 times due to the localized surface plasmon resonance.

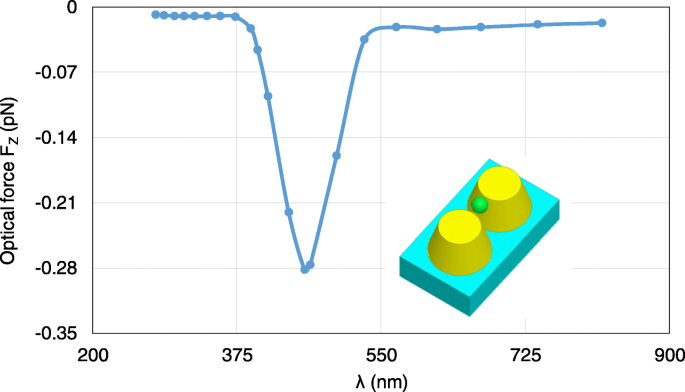
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer, varying with λ . The nanosphere is located at (0, 0, 35 nm)

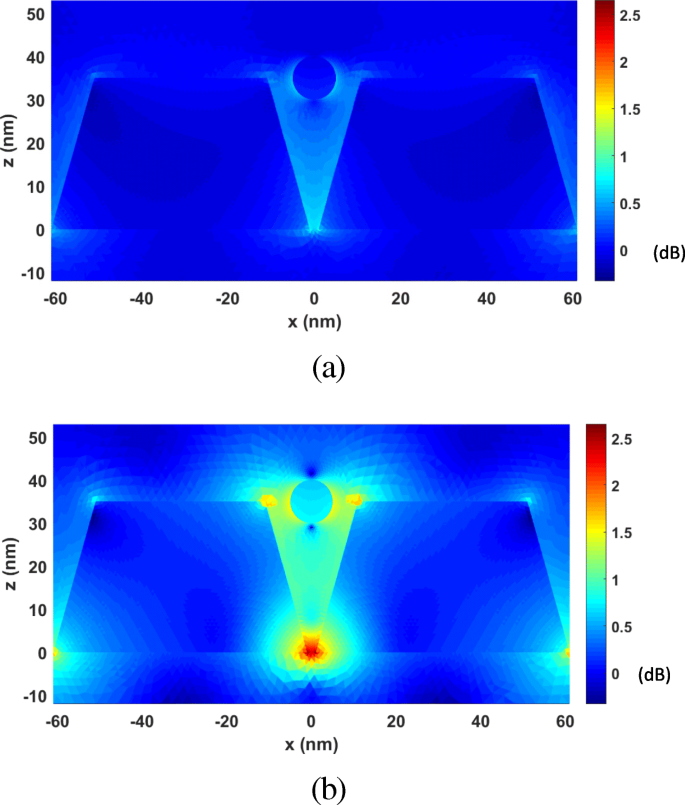
The electric field enhancement distributions on the xoz plane for the system of gold truncated cone dimer. een λ =300 nm (non-resonance wavelength). b λ =464 nm (resonance wavelength)

Then, the location of the nanosphere is changed to 0, 5, and 35 nm to observe the optical force. Figure 12 gives the calculated optical forces exerted on the nanosphere, where obvious y -component of optical force can be observed, while greater z -component of optical force exists. The total optical force still points to the position with the strongest electric field to trap the nanosphere.

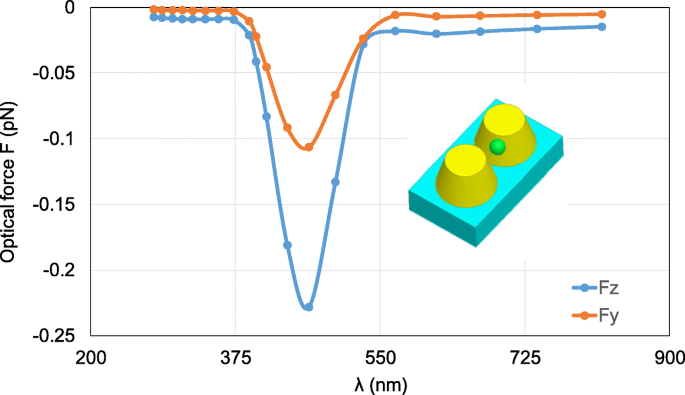
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer varying λ . The nanosphere is located at (0, 5 nm, 35 nm)

Furthermore, we analyze the optical potential with the nanosphere moving from (0, 0, 50 nm) to (0, 0, 20 nm) along the z -as. Here, we consider the axial trapping potential along z -direction, which restricts the motion of the nanoparticle to one dimension and leads to an unambiguous definition of optical potential. Both the optical force and potential are calculated. As can be observed from Fig. 13 a, b, with the nanosphere moving to the dimer gap, the optical force and the optical potential depth obviously increase. At (0, 0, 20 nm), an optical potential depth of 3.8 k _B T is obtained, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

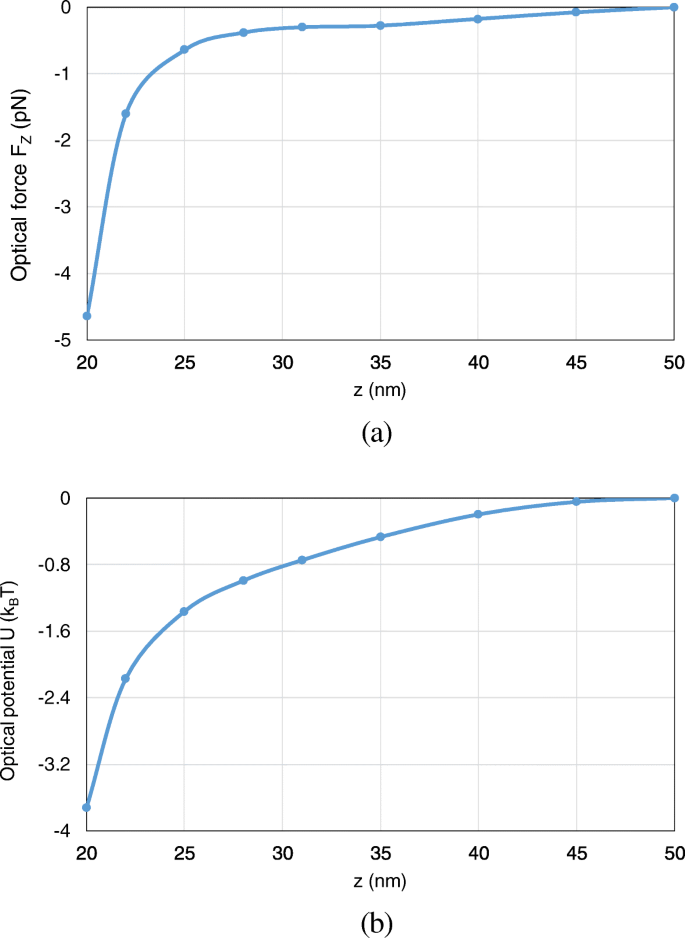
The optical forces and optical potentials exerted on the nanosphere in the system of gold truncated cone dimer, when the nanosphere moves from (0, 0, 50 nm) to (0, 0, 20 nm). een The optical forces. b The optical potentials

Finally, we test the computational costs of the FETI-DP by changing the number of unknowns from 1.0 million to 3.2 million based on different mesh size. In practice, the tests under different mesh density are usually necessary to meet different accuracy requirements. Such a large-scale complex problem brings great challenges to conventional numerical methods. However, the FETI-DP can easily handle this problem. Thirty-two processors are employed for the FETI-DP simulation, while each processor deals with a subdomain. Table 3 reports the computational costs of the FETI-DP. It can be seen that the FETI-DP exhibits high simulation efficiency and low memory requirement.

Conclusion

An FETI-DP method combined with low-rank sparsification is proposed for the prediction and analysis of optical trapping of metal nanoparticles. The proposed method provides fully decoupled subdomain problems, which converts a large-scale complex problem into a series of small-scale simple problems. It is well-suited for parallel computation and can significantly improve the efficiency of numerical simulation. Examples demonstrate that the proposed method exhibits excellent performance of large-scale computation and is well-suited for the fast and accurate simulation of optical trapping at nanoscale.

Beschikbaarheid van gegevens en materialen

All data generated or analyzed during this study are included in this article.

Afkortingen

ABC:: Absorbing boundary condition
DOF:: Degrees of freedom
FDTD:: Tijdsdomein met eindig verschil
FEM:: Eindige elementen methode
FETI-DP:: Dual-primal finite element tearing and interconnecting
MST:: Maxwell stress tensor
MVP:: Matrix-vector product

Magische wiskundige relaties voor nanoclusters—Errata en Addendum Double-Gated Nanohelix als een nieuw afstembaar binair superrooster

Nanomaterialen

Metaal

Hars

vezel

Samengesteld materiaal