Double-Gated Nanohelix als een nieuw afstembaar binair superrooster
Abstract
We onderzoeken theoretisch het probleem van een elektron beperkt tot een nanohelix tussen twee parallelle poorten gemodelleerd als geladen draden. Het dubbel-gated nanohelix-systeem is een binair superrooster met eigenschappen die zeer gevoelig zijn voor de poortspanningen. In het bijzonder vertoont de bandstructuur energiebandovergangen voor bepaalde combinaties van poortspanningen, wat zou kunnen leiden tot quasi-relativistische Dirac-achtige verschijnselen. Onze analyse van optische overgangen die worden veroorzaakt door lineair en circulair gepolariseerd licht, suggereert dat een nanohelix met dubbele poort kan worden gebruikt voor veelzijdige opto-elektronische toepassingen.
Inleiding
Van de gefossiliseerde spiraalvormige buikpotigen die de eerste auteur enthousiast verzamelde in zijn jeugd, tot de verstrengelde DNA-structuur die ongetwijfeld ooit die prehistorische wezens definieerde, de helixgeometrie komt overal in de natuur voor [1]. Geïnspireerd door de complexe functionaliteiten die worden toegeschreven aan de vormen van natuurlijk voorkomende biomoleculen [2-6], wordt verwacht dat andere systemen met spiraalvormige geometrieën die geschikt zijn voor nanotechnologie, rijke fysica zullen opleveren en bijdragen aan nieuwe toepassingen. In de afgelopen drie decennia heeft opmerkelijke vooruitgang in nanofabricagetechnieken geleid tot de realisatie van nanohelices in een groot aantal verschillende systemen, waaronder InGaAs/GaAs [7], Si/SiGe [8], ZnO [9-11], CdS [ 12], SiO2 /SiC [13, 14], en pure koolstof [15–20], evenals II-VI en III-V halfgeleiders [21] (voor de huidige stand van de techniek zie referenties [21–26]). Bijgevolg wordt een overvloed aan verschijnselen verwacht in dergelijke structuren, variërend van exotische transporteigenschappen zoals topologische gekwantiseerde ladingspompen [27, 28], supergeleiding [29] en spinfiltering [30-32], tot moleculaire en nanomechanische rekbare elektronica [33, 34] vanwege piëzo-elektrische effecten [35], detectietoepassingen [36, 37], energie- [38] en waterstofopslag [39] en veldeffecttransistoren [40, 41].
De fascinatie voor op nanohelix gebaseerde apparaten komt uiteindelijk voort uit de inherente periodiciteit die is gecodeerd in de topologie van de helixstructuur. In het bijzonder het onderwerpen van een nanohelix aan een transversaal elektrisch veld (normaal op de helix-as) leidt tot superroostergedrag zoals Bragg-verstrooiing van elektronen op een superperiodieke potentiaal, wat leidt tot een energiesplitsing aan de rand van het superrooster Brillouin-zone tussen de laagste toestanden lineair afstembaar door het elektrische veld [42, 43]. Dit gedrag kan resulteren in Bloch-oscillaties en negatieve differentiële geleiding [44, 45], en kan spin-gepolariseerd transport door helices benadrukken [31, 46], en ook een circulair dichroïsme opleveren dat nuttig is in nanofotonische chiroptische toepassingen [47]. Dit systeem vormt een unair superrooster en opent verder de mogelijkheid om nanohelices te gebruiken als tunneldiodes of Gunn-diodes voor frequentievermenigvuldiging, versterking en generatie of absorptie van straling in het geprezen terahertz-bereik [48-51]. Terwijl het prototypische superrooster meestal wordt gerealiseerd in heterostructuren van afwisselende halfgeleiderlagen met verschillende intrinsieke bandafstanden, worden de parameters van het nanohelix-superrooster volledig gecontroleerd door het externe veld. Daarentegen zijn de vormen van de voormalige conventionele superroosterpotentialen specifiek voor de heterostructuur en, hoewel robuust, bieden ze beperkte mogelijkheden voor manipulatie tijdens de exploitatie ervan zonder het gebruik van grote externe velden. Daarom ligt de aantrekkingskracht van het gebruik van nanohelices als superroosters in plaats hiervan in hun grotere afstembaarheid.
Aan de andere kant, met heterostructuur halfgeleidende superroosters (of zelfs fotonische superroosterstructuren [52-55] en koude atomen in optische roosters [56, 57]) kan men meer gecompliceerde superroostereenheidscellen creëren buiten de eenvoudige kwantumput die wordt geïnduceerd door de elektrisch veld langs de helix. Zelfs de uitbreiding naar een binair superrooster [58-60] (waarbij de eenheidscel wordt onderscheiden door twee verschillende kwantumbronnen en/of barrières) belooft een rijk scala aan fysica, zoals Bloch-Zener-oscillaties [61], die op hun beurt kunnen bijdragen voor afstembare bundelsplitsers en interferometertoepassingen [62]. Het zou dus zeer wenselijk zijn om de externe veldafstembaarheid van een op nanohelix gebaseerd superrooster te combineren met de superieure functionaliteit van een binair superrooster.
In wat volgt, beschrijven we precies zo'n systeem, met een nanohelix gepositioneerd tussen twee parallel-gated geladen draden uitgelijnd met de helix-as. We overwegen de toepassing van een extra transversaal elektrisch veld en laten theoretisch zien dat de poort- en veldbestuurbare potentiaal een binair superrooster vormt langs de eendimensionale helix.
Methoden
Theoretisch model
Laten we beginnen met het bestuderen van het geval van een cirkelvormige nanohelix met een enkelvoudige elektron halfgeleider met N omwentelingen van straal R , toonhoogte p , en totale lengte L =Np . De nanostructuur is gepositioneerd tussen twee parallelle poorten gemodelleerd als geladen draden met de helix-as uitgelijnd langs de z -as en met as en poorten die zich allemaal op hetzelfde vlak bevinden als afgebeeld in Fig. 1. Bovendien beschouwen we een extern transversaal elektrisch veld loodrecht op het poortasvlak \(\mathbf {E}=E_{\bot } \ hat {\mathbf {y}}\) die kan worden gebruikt om de reflectiesymmetrie van de potentiaal boven het vlak ten opzichte van de potentiaal onder het vlak te doorbreken. We werken in spiraalvormige coördinaten, parametrisch beschreven via r =(x,y ,z )=(R cos(s φ ),R sin(s φ ),ρ φ ), waarbij de dynamische hoekcoördinaat φ =z /ρ hangt alleen af van de afstand langs de as van de helix met ρ =p /2π , en s =±1 geeft respectievelijk een links- of rechtshandige helix aan. In dit werk beschouwen we een linkshandige helix s =1. In het kader van het effectieve massamodel is het energiespectrum ε ν van de ν de eigentoestand van een elektron in een helix onder invloed van dergelijke externe potentialen wordt gevonden uit de Schrödingervergelijking:
$$ -\thinspace \frac{\hbar^{2}}{2M^{*}\rho^{2}}\frac{d^{2}}{d\varphi^{2}}\psi_{\ nu} +\left[V_{g} (\varphi) + V_{\bot} (\varphi) \right]\psi_{\nu} =\varepsilon_{\nu} \psi_{\nu} $$ (1 )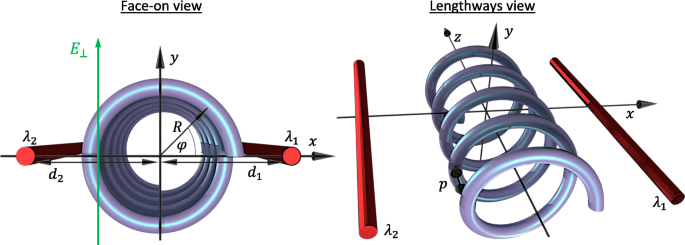
Diagram van de geometrie en parameters van het systeem vanuit zowel face-on als lengteperspectieven. R is de straal van de helix, en d 1 en d 2 zijn de afstanden van de geladen draden van de helix-as met ladingsdichtheden λ 1 en λ 2 , respectievelijk. De ruimtelijke coördinaat φ beschrijft de hoekpositie op de helix van face-on en is gerelateerd aan de z -coördinaat via φ =2π z /p met p de toonhoogte van de helix. Een transversaal elektrisch veld E ⊥ wordt parallel aan de y . toegepast -as
waarbij we de effectieve elektronenmassa M . geometrisch hebben gerenormaliseerd e naar M ∗ =M e (1+R 2 /ρ 2 ) om alles uit te drukken in termen van de coördinaat langs de helix-as (onthoud dat φ =z /ρ ) wat handiger is voor externe potentialen. Hier, V ⊥ (φ )=−eE ⊥ R zonde(φ ) is de bijdrage van het transversale elektrische veld gericht langs de y -as zodanig dat V ⊥ (π /2)<0. De potentiaal van de poorten is V g (φ )=−e [Φ 1 (φ )+Φ 2 (φ )] met de elektrostatische potentiaal die wordt gevoeld door een elektron langs de helix als gevolg van een individueel geladen draad gegeven door Φ ik (φ )=−λ ik k ln(r ik /d ik ). Hier, ik =1,2 markeert de draden, λ ik is de lineaire ladingsdichtheid op een draad, en \(k =1/2\pi \tilde {\epsilon }\) met \(\tilde {\epsilon }\) de absolute permittiviteit. De loodrechte afstand van een testlading tot een bepaalde draad wordt gegeven door \(r_{i}=[d^{2}_{i}+R^{2} + 2(-1)^{i}d_{i }R\cos (\varphi)]^{1/2}\), met d ik aanduiding van de corresponderende afstand van de draad tot de as van de helix. We hebben een nulpoort-geïnduceerd potentieel gedefinieerd dat zich langs de as van de helix bevindt. De totale eendimensionale potentiaal V T (φ )=V g (φ )+V ⊥ (φ ) is duidelijk periodiek V T (φ )=V T (φ +2π n ) met punt 2π in het algemeen (wat overeenkomt met een periode van p met betrekking tot de coördinaat z ). Deze periode is aanzienlijk groter dan de interatomaire afstand en geeft aanleiding tot typische superroostereffecten. Deze letter verschilt van een nanohelix in een transversaal elektrisch veld (dat kan worden gereproduceerd met V T (φ )=V ⊥ (φ ) hier) voornamelijk door de herhaalde eenheidscel van het superrooster te manipuleren via de dubbele poortpotentiaal V g (φ ). De limiet nemen p →0, we keren terug naar het deeltje op een ringbeeld onderworpen aan twee elektrostatische poorten [63, 64]. De benadering R . maken /d ik ≪1, we kunnen V . uitbreiden g (φ ) tot tweede bestelling in cos(φ ), en bij het transformeren van Eq. 1 in dimensieloze vorm komen we bij
$$ {\begin{aligned} \frac{d^{2} \psi_{\nu}}{d\varphi^{2}}+\left[\epsilon_{\nu} + 2A_{g}\cos( \varphi) + 2B_{g}\cos(2\varphi) + 2C_{\bot} \sin(\varphi) \right]\psi_{\nu} =0, \end{aligned}} $$ (2)met de hoeveelheden in eenheden van de energieschaal \(\varepsilon _{0}(\rho) =\hbar ^{2} / 2 M^{*} \rho ^{2}\) gedefinieerd als
$$\begin{array}{@{}rcl@{}} A_{g} &=&\beta\frac{\left(d_{1}^{2} +R^{2}\right)}{ d_{1} R}(1-\gamma), \qquad B_{g} =\frac{\beta}{2}\left(1+\frac{\lambda_{1}}{\lambda_{2}} \gamma^{2}\right), \\ C_{\bot} &=&e E_{\bot} R /2\varepsilon_{0}(\rho), \qquad \qquad \qquad \; \epsilon_{\nu} =\frac{\varepsilon_{\nu}}{\varepsilon_{0}(\rho)}. \end{array} $$ (3)Hier, \(\beta =ek d_{1}^{2} R^{2} \lambda _{1} /2\left (d_{1}^{2} +R^{2}\right)^ {2}\varepsilon _{0}(\rho) \) karakteriseert de bijdrage van poort 1 terwijl de asymmetrieparameter \(\gamma =\lambda _{2} d_{2} \left (d_{1}^{2 } +R^{2}\right)/\lambda _{1} d_{1} \left (d_{2}^{2} + R^{2}\right)\) kenmerkt de relatieve bijdrage van gate 2 , met γ =1 komt overeen met gelijke poortbijdragen aan de potentiaal (resulterend in A g =0). Opgemerkt moet worden dat de onvermijdelijke asymmetrie veroorzaakt door de moeilijkheid bij het onderhouden van d 1 =d 2 kan worden gecompenseerd door λ . te manipuleren 1 en λ 2 . In deze brief beperken we ons tot het overwegen van γ ≤1 (dat is |Φ 1 |>|Φ 2 |) aangezien de asymmetrieparameter groter is dan één, kan worden toegewezen aan een equivalent systeem onder één via een eenvoudige uitwisseling van de indices die de poorten labelen en een overeenkomstige verschuiving in perspectief φ →φ ±π . We houden ook alleen rekening met C ⊥ ≥0 vanwege de symmetrie van negatieve C ⊥ met betrekking tot een dergelijke coördinaatvertaling in φ , en A g ≥0, B g >0 (d.w.z. alleen positieve ladingsdichtheden op de draden β>0) aangezien elk potentieel landschap met negatief geladen poorten kan worden gereproduceerd met de juiste combinatie van parameters van positief geladen poorten. In Fig. 2 plotten we de dimensieloze potentiaal V T (φ )/ε 0 (ρ ), met de kracht van de π -periodieke potentiële component vastgesteld op B g =0,2, voor verschillende combinaties van de verstoringsparameters van de verdubbelde periode A g en C ⊥ . We zien dat de totale externe potentiaal een binair superrooster induceert langs φ , met een dubbele kwantumput (DQW) als eenheidscel blauw gemarkeerd. Dit kan kwalitatief verschillende vormen aannemen door de relatieve poortbijdragen te manipuleren γ en transversaal elektrisch veld E ⊥ . De eenheidscel is in wezen een enkelvoudige put onder equivalente poortbijdragen (γ =1) en geen transversaal elektrisch veld E ⊥ =0 (zoals in Fig. 2a voor A g =C ⊥ =0). E . repareren ⊥ =0, met een sterkere bijdrage van poort 1 (γ <1), wordt de eenheidscel een DQW met verschillende putminima en gedegenereerde barrièremaxima (Fig. 2b waarbij A g =0.1 en C ⊥ =0). Om de DQW-minima gedegenereerd te houden en de twee potentiële barrières ten opzichte van elkaar te manipuleren, zijn daarentegen symmetrische poortbijdragen vereist (γ =1) in een elektrisch veld dat niet nul is E ⊥ ≠0 (Fig. 2c met A g =0 en C ⊥ =0,1). Asymmetrische poortbijdragen combineren (γ <1) met E ⊥ ≠0 produceert een DQW met verschillende potentiaalputminima en verschillende barrières (zoals te zien in figuur 2d waar beide A g =C ⊥ =0,1). Dit leidt tot kwalitatief verschillend en rijk gedrag, zoals we in de volgende paragrafen zullen zien.
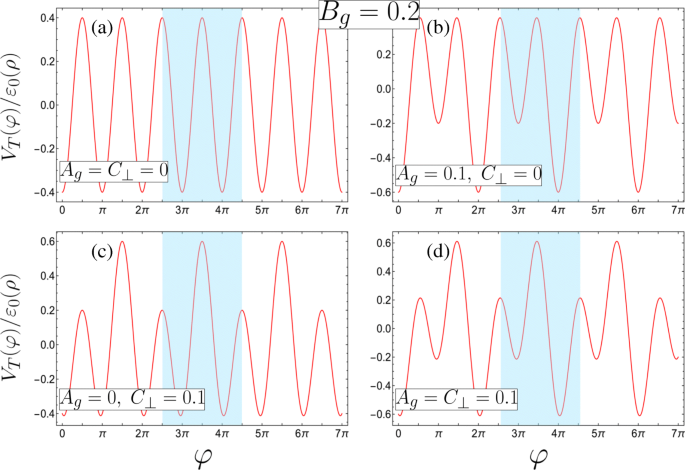
De vier mogelijke superroosterpotentiaalconfiguraties met de eenheidscellen blauw gemarkeerd (gedefinieerd in termen van de dimensieloze parameters, zie vergelijking 3 voor de overeenkomstige vereisten van de fysieke parameters, en allemaal met B g =0,2). een Een unair superrooster met gedegenereerde minima en maxima in de eenheidscel (A g =C ⊥ =0). b –d Binaire superroosters gevormd uit een van beide b een asymmetrische DQW met verschillende minima en interne reflectiesymmetrie rond beide minima als gevolg van gedegenereerde maxima (A g =0.1, C ⊥ =0), c een symmetrische DQW met alleen gedegenereerde minima (A g =0, C ⊥ =0.1), of d een asymmetrische DQW met verschillende minima en maxima (A g =C ⊥ =0.1)
Oplossingen als een oneindige matrix
Oplossingen voor vgl. 2 kan worden gevonden in termen van de Bloch-functies
$$ \psi_{n,q}(\varphi)=(2\pi N \rho)^{-\frac{1}{2}}e^{iq \varphi}\sum_{m} c^{( n)}_{m,q} e^{im \varphi}, $$ (4)waar de q =k z ρ is de dimensieloze vorm van het quasi-momentum van het elektron k z langs de as van de helix, n geeft de subband aan, en de prefactor komt voort uit normalisatie in termen van φ :\(\rho \int _{0}^{2\pi N}|\psi _{n,q}(\varphi)|^{2} d\varphi =1\). We maken gebruik van de orthogonaliteit van de exponentiële functies door de resulterende uitdrukking te vermenigvuldigen met \(e^{im^{\prime } \varphi }/2\pi \) en te integreren met betrekking tot φ , waar m ′ is een geheel getal, zodat we tot een oneindige reeks gelijktijdige vergelijkingen komen voor de coëfficiënten \(c^{(n)}_{m,q}\),
$$ {\begin{aligned} &\left[(q+m)^{2}-\epsilon_{n}\right]c^{(n)}_{m} - \left(A_{g} - i C_{\bot} \right)c^{(n)}_{m-1} - \left(A_{g} + i C_{\bot} \right)c^{(n)}_{m +1}\\ &\quad- B_{g}\left(c^{(n)}_{m+2}+c^{(n)}_{m-2} \right)=0, \ einde{uitgelijnd}} $$ (5)waar voor de duidelijkheid de q -subscript-notatie is verwijderd, ε n,q ≡ε n en \(c_{m}^{(n)}\equiv c_{m,q}^{(n)} \). Vergelijking 5 vertegenwoordigt een oneindige vijfhoekige matrix waarin het duidelijk is dat het systeem periodiek is in q , en we kunnen onze overwegingen beperken tot de eerste Brillouin-zone gedefinieerd door − 1/2≤q 1/2. Bij afwezigheid van het superroosterpotentieel A g =B g =C ⊥ =0, de eigenwaarden worden dan opgesomd door m gegeven door ε m =(m +q ) 2 en we herkennen m het kwantumgetal van het impulsmoment dat hoort bij een vrij elektron op een helix. We zien uit vgl. 5 dat wanneer A g =C ⊥ =0 staat alleen met Δ m =±2 zijn gemengd, terwijl de vorming van een DQW-eenheidscel met verschillende putminima of barrières, bereikt via A g ≠0 en/of C ⊥ ≠0, mengt ook toestanden met Δ m =± 1. Interessant is dat het systeem van een elektron op een helix onder een externe transversale potentiaal (die varieert over één omwenteling van de helix) wiskundig equivalent is aan een elektron op een kwantumring doorboord door een magnetisch veld en onderworpen aan een potentiaal met dezelfde functionele vorm variërend langs de hoekcoördinaat; bijv. zie Ref. [65-67] of vergelijk bijvoorbeeld Refs. [42–45] met [68–70]. Voor een ring, de rol van q hier wordt opgenomen door de magnetische flux. Daarom is precies dezelfde analyse in dit werk van toepassing op het probleem van een dubbel-gated kwantumring [63–66], als de ring zou worden doorboord door een magnetische flux.
Afkappen en numeriek diagonaliseren van de matrix die overeenkomt met Vgl. 5 geeft de n de eigenenergieën van de subband ε n en coëfficiënten \(c_{m}^{(n)}\) voor elke waarde van q . We passen een truncatie toe op |m |=10, veilig in de wetenschap dat elke toename van de matrixgrootte geen merkbare verandering in de laagste subbanden oplevert.
Resultaten en discussie
Double-gated nanohelix bandstructuur
We plotten in Fig. 3 de energiedispersie van de laagste banden voor verschillende combinaties van parameters. Afhankelijk van de vorm van het superrooster vinden we een opmerkelijke variëteit in het dispersiegedrag, en voor sommige specifieke combinaties van parameters ontdekken we energiebandovergangen voor bepaalde subbanden aan de rand van de Brillouin-zone (Fig. 3a en c) of aan de midden van de Brillouin-zone (Fig. 3b en d).
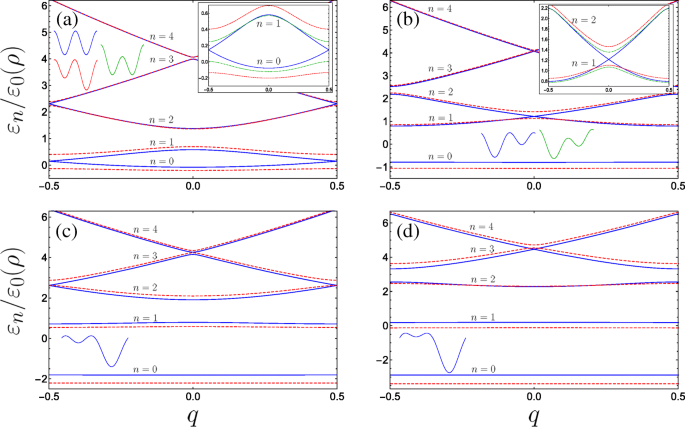
Bandstructuur voor dubbel-gated nanohelix-systeem voor verschillende combinaties van de dimensieloze parameters (met B g =0,4 overal vast):a Effen blauwe (rood onderbroken) plots A g =0 &C ⊥ =0 (A g =0,2 &C ⊥ =0), plot de inzet bovendien het gedrag van de onderste twee subbanden die onderhevig zijn aan het transversale elektrische veld met A g =0 &C ⊥ =0,2 als de gestippelde groene curve. b Effen blauwe (rood onderbroken) plots A g =0.63 &C ⊥ =0 (A g =0,8 &C ⊥ =0) waar de blauwe curve het eerste incident van resonantie weergeeft (zie tekst) met energiebanden die elkaar kruisen in het midden van de Brillouin-zone, vergelijkt de inzet het gedrag van de onderste geëxciteerde twee subbanden met het geval waarin A g =0.63 &C ⊥ =0,2 als de gestippelde groene curve. c Effen blauwe (rood onderbroken) plots A g =1.26 &C ⊥ =0 (A g =1.5 &C ⊥ =0) waarbij de blauwe curve het tweede resonantie-incident weergeeft met energiekloven die sluiten aan de rand van de Brillouin voor hogere banden. d De derde resonantie en hogere subband-minigaten sluiten in het midden, met effen blauw (rood onderbroken) als A g =1.9 &C ⊥ =0 (A g =2.2 &C ⊥ =0). De vormen van de eenheidscellen zijn geschetst, n somt de banden op en de as van de inzetstukken is hetzelfde als de hoofdgrafieken
Lage veld verdubbelde periode verstoring
Wanneer A g =C ⊥ =0, vormt de eenheidscel twee equivalente kwantumputten, en bijgevolg ontstaat op natuurlijke wijze het verschijnen van paren banden die elkaar raken aan de randen van de Brillouin-zone. Inderdaad, het nemen van slechts één putje als eenheidscel halveert de superroosterperiode en resulteert in een verdubbeling van de Brillouin-zone − 1≤q ≤1. We zouden dan het gebruikelijke unaire superroosterbanddiagram waarnemen, waarin de bandafstand tussen de grond en de eerste banden op q =1 wordt hier gegeven via de band gap tussen n =1 en n =2 bij q =0 en zou lineair zijn in B g uit de storingstheorie. Toch presenteren we een beschrijving van de bandstructuur op |q |=1/2 in de afbeelding van de DQW-eenheidscel met behulp van matrixalgebra in de bijlage. Zoals te zien is in de inzet van figuur 3a, opent de introductie van een van de potentiaaltermen met dubbele periode een bandgap aan de rand van de Brillouin-zone. De eenheidscel van symmetrische poortbijdragen (A g =0) behoudt de vorm van een symmetrische DQW onder toepassing van een transversaal veld C ⊥ loodrecht op de as van de helix-poort, met één potentiaalbarrière gewijzigd ten opzichte van de andere (aangegeven door de groene DQW-schets in figuur 3a). Terwijl C ⊥ een band gap opent, is de wijziging van de dispersie aanzienlijk minder gevoelig dan die van een vergelijkbare grootte van toegepaste A g . Dit is te zien aan de kleinere bandgap bij |q |=1/2 voor de gestippelde groene lijn in de inzet van Fig. 3a (met A g =0 en C ⊥ =0,2) vergeleken met de grotere opening voor de gestippelde rode curve (die is voor A g =0.2 en C ⊥ =0). Om dit gedrag te benadrukken, plot in Fig. 4a de grootte van de energiekloof bij |q |=1/2 tussen de twee laagste subbanden \(\Delta \varepsilon _{01}^{(q=1/2)}/\varepsilon _{0}(\rho)\) voor vaste B g =0.25 als functie van beide C ⊥ (met A g =0) en A g (met C ⊥ =0), als respectievelijk groene en rode stippellijnen met stippen. In nul transversaal elektrisch veld en asymmetrische poortpotentialen (C ⊥ =0 en A g ≠0), is de eenheidscel dan een asymmetrische DQW, zij het met interne reflectiesymmetrie rond beide putminima vanwege de equivalente barrières. We kunnen dan de hogere gevoeligheid van de bandgap voor het veranderen van A . begrijpen g door de eigenschappen van de geïsoleerde DQW-eenheidscel te beschouwen waaruit het superrooster is opgebouwd. Met A g =C ⊥ =0, bij |q |=1/2 (de randen van de Brillouin-zone), zullen de Bloch-toestanden gevormd uit de grond en de eerste aangeslagen toestand van de geïsoleerde DQW-eenheidscel (zie het blauwe schema en de bijbehorende golffuncties in Fig. 4a) alleen verschillen door een willekeurige fase. Deze situatie komt overeen met de gapless blauwe dispersiecurve van figuur 3a. Zoals schematisch weergegeven in Fig. 4a via de groene DQW-schets, C ⊥ vermindert de relatieve maxima van een van de barrières ten opzichte van de andere, terwijl de DQW-minima gedegenereerd blijven. Als zodanig wordt de grondtoestand van de geïsoleerde DQW alleen gewijzigd door een lichte toename van de kansverdeling onder de kleinere potentiaalbarrière (die slechts een kleine verlaging van de energie opbrengt in vergelijking met de onverstoorde grondtoestand), en de eerste aangeslagen toestand blijft in wezen ongewijzigd omdat het knooppunt zich onder de barrière bevindt en niet gevoelig is voor de variatie ervan. De Bloch-toestanden aan de rand van de Brillouin-zone die zijn opgebouwd uit deze grond- en eerste aangeslagen toestanden verschillen van het onverstoorde geval alleen in het verminderde verval van de golffunctie van de grondtoestand onder de kleinere barrière (vergelijk de groene DQW met de blauwe DQW in Afb. 4a). A . wijzigen g manipuleert de relatieve posities van de DQW-minima terwijl de barrières degenereren. De golffuncties van de twee laagste geïsoleerde DQW-toestanden verschillen aanzienlijk, waarbij de grondtoestand neigt naar de gelokaliseerde grondtoestand van de enkelvoudige diepere put en de eerste aangeslagen toestand neigt naar de gelokaliseerde grondtoestand van de ondiepere put [71]. Terwijl de verstoring de energie van de grondtoestand verlaagt, neemt de energie van de eerste aangeslagen toestand relatief toe naarmate de minima van de ondiepere put omhoog worden verschoven met toenemende A g , wat resulteert in een hogere gevoeligheid van de bandgapgrootte met betrekking tot A g . In het bijzonder wordt een deeltje in de grondsubband snel opgesloten in de buurt van de bodem van de diepste potentiaalbron met toenemende A g . De laagste band benadert daarom een dispersieloze vlakke band sneller dan in het geval van het transversale veld, wat kan leiden tot elektronische instabiliteiten en sterke interactie-effecten die gepaard gaan met de hoge dichtheid van toestanden [72].
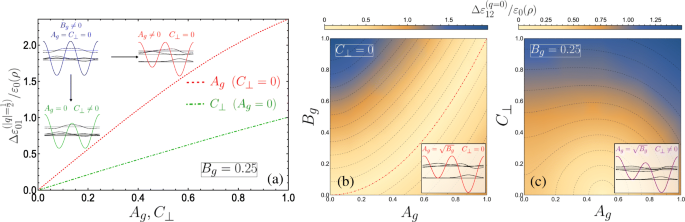
een Bandafstand tussen grond en eerste subbanden als functie van A g (C ⊥ ) uitgezet als rood gestippeld (groen gestippeld), hier B g =0,25. De diagrammen geven de invloed aan van de verschillende verstoringen op de geïsoleerde DQW-eenheidscel en eigentoestanden. b –c Bandgapgrootte tussen eerste en tweede subband aangegeven via een 2D-dichtheidsplot als functie van; b A g en B g voor C ⊥ =0, en c A g en C ⊥ met vaste B g =0,25. b Aangrenzende iso-energiecontourlijnen geven een verschil aan van 0,17, met een nulafstand gegeven door de rode stippellijn met stippellijnen voor \(A_{g}=\sqrt {B_{g}}\), terwijl c het verschil is 0,13 met nulopening in het midden van de kleinste halve cirkelcontour (0,5,0). De diagrammen schetsen de geïsoleerde DQW en eigentoestanden. Hybridisatie vindt niet plaats tussen de s -like en p -achtige resonantie gelokaliseerde individuele puttoestanden in b , maar wel in c doordat het elektrische veld de ene barrière verandert ten opzichte van de andere
Overgangen energieband
Het is nogal opmerkelijk om te zien dat als we C . houden ⊥ =0 en verhoog A g , terwijl aanvankelijk alle degeneraties worden opgeheven, worden daaropvolgende banden met hogere energie elkaar afwisselend tussen het midden en de rand van de Brillouin-zone gebracht (let op het gedrag van afwisselende blauwe en gestreepte rode curven die zich uitstrekken van Fig. 3a tot en met d). Fysiek kunnen we de verdwijnende bandkloof begrijpen in termen van interacties van de gelokaliseerde golffuncties in de eenheidscel. Wanneer de asymmetrische DQW-potentiaal zodanig is dat de grondtoestand in de ondiepere put (s -achtige orbitaal) resoneert met de eerste aangeslagen toestand in de diepere put (p -achtige orbitaal), op q =0 vanwege de reflectiesymmetrie rond het midden van beide putten, voorkomen de tegengestelde pariteiten van deze toestanden de gebruikelijke tunnelkoppeling ertussen, en bijgevolg vallen de aangeslagen toestanden die uit deze orbitalen zijn geconstrueerd samen (blauwe curven in figuur 3b). Dit doet denken aan zogenaamde s −p resonanties in optische roosters [73, 74]. Evenzo, als de parameters zodanig zijn dat de gelokaliseerde grondtoestand in de ondiepe put resoneert met een aangeslagen toestand in de diepere put met dezelfde pariteit, dan bij |q |=1/2, onderdrukt de aanwezigheid van de Bloch-fase de gebruikelijke hybridisatie tussen deze twee aangrenzende gelokaliseerde puttoestanden volledig en wordt de bandafstand gesloten (zoals getoond in figuur 3c voor resonantie van grond met tweede aangeslagen toestand). In de taal van verstrooiing van het periodieke potentieel; de bandgap is gesloten vanwege de volledige destructieve interferentie van de tweede-orde Bragg-verstrooiingsamplitudes van de cos(φ ) potentiële en eerste-orde verstrooiingsamplitudes van de cos(2φ ) potentieel [75-77].
We kunnen het bestaan van energiebandovergangen kwantitatief aantonen (voor een transversaal elektrisch veld van nul) in zowel het midden als de rand van de Brillouin-zone door terug te keren naar Vgl. 2, die herkenbaar is als de Whittaker-Hill-vergelijking wanneer C ⊥ =0 [78]. De Bloch-functies Vgl. 4 gehoorzamen aan verwrongen periodieke randvoorwaarden ψ n,q (φ +2π )=exp(2π iq )ψ n,q (φ ). In het bijzonder, wanneer q =0 formele oplossingen voor Vgl. 2 zijn 2π -periodiek, terwijl wanneer |q |=1/2 oplossingen zijn 2π -antiperiodiek (en daarom zullen we zoeken naar 4π -periodieke oplossingen). Specifiek, Vgl. 2 met C ⊥ =0 kan worden toegewezen aan de vergelijking van Ince [79, 80], die quasi-exact oplosbaar is, door de golffunctie uit te drukken als het product van de asymptotische oplossing van Vgl. 2 en een onbekende functie \(\psi _{n,q}(\varphi) =\exp \left [ -2\sqrt {B_{g}}\cos (\varphi)\right ]\Phi _{n, q}(\varphi)\), zodat
$$ \frac{d^{2} \Phi_{n,q}}{d \varphi^{2}} + \frac{\xi}{2} \sin(\varphi)\frac{d\Phi_{ n,q}}{d\varphi} +\frac{1}{4}\left[ \eta_{n,q} - p\xi\cos(\varphi) \right]\Phi_{n,q} =0, $$ (6)waar we de hulpparameters \(\xi =8\sqrt {B_{g}}\) hebben gedefinieerd, η n,q =4ε n,q +8B g , \(-p \xi =8A_{g}+8\sqrt {B_{g}}\), en Φ n,q (φ ) handhaaft de noodzakelijke verwrongen periodiciteit van elke oplossing (merk op dat hier p is niet de helixsteek). Bovendien, aangezien het superroosterpotentieel hier invariant is onder de transformatie φ →− φ , de oplossingen voor q =0 en q =1/2 kan worden gescheiden in oneven en even pariteit, zodat de volgende trigonometrische reeks
$$ \Phi_{n,0}^{(e)}(\varphi) =\sum_{l=0}a^{(n)}_{l}\cos(l\varphi), $$ (7a ) $$ \Phi_{n,0}^{(o)}(\varphi) =\sum_{l=0}b^{(n)}_{l+1}\sin[(l+1)\ varphi], $$ (7b) $$ \Phi_{n,\frac{1}{2}}^{(e)}(\varphi) =\sum_{l=0}\widetilde{a}^{( n)}_{l}\cos\left[\left(l+\frac{1}{2}\right)\varphi\right], $$ (7c) $$ \Phi_{n,\frac{1} {2}}^{(o)}(\varphi) =\sum_{l=0}\widetilde{b}^{(n)}_{l+1}\sin\left[\left(l+\frac {1}{2}\right)\varphi\right], $$ (7d)bestrijken de formele oplossingen, en we merken op dat oplossingen voor q =−1/2 zijn hetzelfde als voor q =1/2. Hier, de superscripts e en o label de functies als respectievelijk even en oneven, en n verwijst nog steeds naar de n de subband, wat ook de n . is de eigentoestand voor deze gespecificeerde q waarden. Vervanging van deze in Vgl. 6 resulteert in drie-term recursierelaties voor de fouriercoëfficiënten. De q =0 even oplossing levert
$$ -\eta_{n,0}^{(e)}a^{(n)}_{0} + \xi\left(\frac{p}{2} +1 \right) a^{( n)}_{2} =0, $$ (8a) $$ \xi pa^{(n)}_{0} + \left(4 - \eta_{n,0}^{(e)} \ rechts)a^{(n)}_{2} + \xi \left(\frac{p}{2} +2 \right)a^{(n)}_{4}=0, $$ (8b ) $$ {\begin{aligned} &\xi \left(\frac{p}{2} - l +1 \right)a^{(n)}_{2l-2} + \left(4l^{ 2} - \eta_{n,0}^{(e)} \right)a^{(n)}_{2l}\\ &\quad+\xi \left(\frac{p}{2} + l +1 \right)a^{(n)}_{2l+2} =0, \qquad (l \ge 2) \end{aligned}} $$ (8c)en de bijbehorende recursierelaties voor de oneven oplossing voor q =0 is
$$ (4 - \eta_{n,0}^{(o)})b^{(n)}_{2} + \xi \left(\frac{p}{2} +2 \right)b ^{(n)}_{4} =0, $$ (9a) $$ {\begin{aligned} &\xi \left(\frac{p}{2} - l +1 \right)b^{ (n)}_{2l-2} + \left(4l^{2} - \eta_{n,0}^{(o)} \right)b^{(n)}_{2l} +\xi \left(\frac{p}{2} + l +1 \right)b^{(n)}_{2l+2}\\ &=0. \qquad (l \ge 2) \end{aligned} } $$ (9b)De q =1/2 even oplossing geeft
$$ \left[ 1 -\eta_{n,\frac{1}{2}}^{(e)} +\frac{\xi}{2}(p+1) \right]\widetilde{a}^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{a}^{(n)}_{3}=0, $$ (10a) $$ {}{\begin{aligned} &\frac{\xi}{2}(p-2l +1)\widetilde{a}^{(n)}_{2l-1}+\left[(2l+1)^{2} - \eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{a}^{(n)}_{2l+1}\\ &\quad+ \frac{\xi}{2}(p+2l+3)\widetilde{a}^{(n)}_{2l+3}=0, \qquad (l \ge 1) \end{aligned}} $$ (10b)and the q =1/2 odd solution gives
$$ \left[ 1 -\eta_{n,\frac{1}{2}}^{(e)} -\frac{\xi}{2}(p+1) \right]\widetilde{b}^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{b}^{(n)}_{3}=0 $$ (11a) $$ {}{\begin{aligned} &\frac{\xi}{2}(p-2l+1)\widetilde{b}^{(n)}_{2l-1}+\left[(2l+1)^{2} -\eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{b}^{(n)}_{2l+1}\\&\quad + \frac{\xi}{2}(p+2l+3)\widetilde{b}^{(n)}_{2l+3}=0. \qquad (l \ge 1) \end{aligned}} $$ (11b)Consider then Eqs. (8c) and (9b) for the q =0 solutions. The series solutions (7a) and (7b) can clearly be made to terminate if p is 0 or an even positive integer. The resulting polynomials are referred to as Ince polynomials. The remaining solutions for higher eigenvalues are simultaneously double degenerate and correspond to the energy crossings observed at q =0 for certain parameters. The existence of these degeneracies can be seen by looking at the diagonalizable matrices describing the recursion relations for a l en b l :
$$ \boldsymbol{\mathcal{A}} =\left[ \begin{array}{ccccc} 0 &\xi\left(\frac{p}{2} +1 \right) &0 &0 &\hdots \\ \xi p &4 &\xi\left(\frac{p}{2} +2 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \end{array} \right]\!, $$ (12)and
$$ \boldsymbol{\mathcal{B}} =\left[ \begin{array}{ccccc} 4 &\xi\left(\frac{p}{2} +2 \right) &0 &0 &\hdots \\ \xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} -2 \right) &36 &\xi\left(\frac{p}{2} +4 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \\ \end{array} \right]\! $$ (13)respectievelijk. Either of the above tridiagonal matrices can be broken into tridiagonal sub-matrices if a leading off-diagonal matrix element is equal to zero, i.e. if p is an even number. The matrices will decompose into two tridiagonal blocks, one smaller finite matrix \(\boldsymbol {\mathcal {A}_{1}}\) (\(\boldsymbol {\mathcal {B}_{1}}\)) and a remaining infinite matrix \(\boldsymbol {\mathcal {A}_{2}}\) (\(\boldsymbol {\mathcal {B}_{2}}\)). From the theory of tridiagonal matrices the corresponding eigenvalue spectra for each matrix is then \(\eta (\boldsymbol {\mathcal {A}}) =\eta (\boldsymbol {\mathcal {A}_{1}}) \cup \eta (\boldsymbol {\mathcal {A}_{2}})\) and \(\eta (\boldsymbol {\mathcal {B}}) =\eta (\boldsymbol {\mathcal {B}_{1}}) \cup \eta (\boldsymbol {\mathcal {B}_{2}})\). The smaller finite matrices are analytically diagonalizable in principle, giving exact eigenvalues, and their corresponding finite length eigenvectors define the fourier coefficients yielding Ince polynomials via Eq. 7. We can see that for a given even integer p , the remaining infinite tridiagonal matrices are the same \(\boldsymbol {\mathcal {A}_{2}}=\boldsymbol {\mathcal {B}_{2}}\equiv \boldsymbol {\mathcal {D}}\) which results in the double degenerate eigenvalues. To be clear, we provide an example of when p =2 in the Appendix.
In the same way, when p is a positive odd integer the series solutions (7c) and (7d) can be made to terminate, and the matrices corresponding to \(\widetilde {a}_{l}\) and \(\widetilde {b}_{l}\) share eigenvalues resulting in the closing of higher subbands at the edge of the Brillouin zone q =± 1/2. From the definitions of the auxiliary parameters in Eq. 6, we have
$$ A_{g} =(p+1)\sqrt{B_{g}}, $$ (14)which defines the condition for exactly-solvable solutions for the lower lying solutions and simultaneously the existence of higher double degenerate eigenvalues above the p th subband, with p =0 or an even positive integer corresponding to crossings at the centre of the Brillouin zone, while crossings at the edge require p to be an odd positive integer. Figure 4b plots the size of the band gap between the first and second subbands \(\Delta \varepsilon _{12}^{(q=0)}/\varepsilon _{0}(\rho)\) as a function of A g en B g , with the dot-dashed red contour line corresponding to Eq. 14 for p =0. The schematic indicates the appropriate eigenstates of the isolated DQW at the p =0 resonance.
The application of a small transverse field C ⊥ breaks the reflection symmetry of the system, permitting hybridization of the localized well states of the isolated DQW which results in a significant change at points of degeneracy, as can be seen by comparing the schematic depicted in Fig. 4b with that in c (see also inset of Fig. 3b). We plot in Fig. 4c the behaviour of the band gap between the first and second subbands as a function of A g en C ⊥ . Here we see that the band gap is more sensitive to C ⊥ due to the significant change in the isolated DQW eigenstates by lowering one barrier with respect to the other. This behaviour is notably the converse of the parameter sensitivity for the band gap between the ground and first subbands. By degenerate perturbation theory, it can be shown that this induced band gap is linear in C ⊥ for the lowest crossing bands when p =0, and to higher order with increasing p . Finally, within the vicinity of the crossings, e.g. for small q about q =0 in Fig. 3a, the dispersions could be approximated as a quasi-relativistic linear dispersion yielding Dirac-like physics, which could permit superfluiditiy [81] for example. The advantage in using nanohelices lies in introducing such phenomena to portable nanostructure based devices, while also exhibiting unusual responses of the charge carriers to circularly polarized radiation [44, 45, 82–85] (or indeed magnetic fields [86, 87]) due to the helical spatial confinement.
Optical transitions
In order to understand how our double-gated nanohelix system interacts with electromagnetic radiation, we study the inter-subband momentum operator matrix element \(T^{g\rightarrow f}_{j} =\langle {f}|\boldsymbol {\hat {j}} \cdot \boldsymbol {\hat {P}}_{j} |{g}\), which is proportional to the corresponding transition dipole moment, and dictates the transition rate between subbands ψ f and ψ g . Here, \(\boldsymbol {\hat {j}}\) is the projection of the radiation polarization vector onto the coordinate axes (j =x,y ,z ) and the respective self-adjoint momentum operators are [44, 45, 82–84]
$$ \boldsymbol{\hat{P}}_{x} =\boldsymbol{\hat{x}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\sin(\varphi)\frac{d}{d\varphi} + \frac{1}{2}\cos(\varphi) \right], $$ (15a) $$ \boldsymbol{\hat{P}}_{y}=-\boldsymbol{\hat{y}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\cos(\varphi)\frac{d}{d\varphi} - \frac{1}{2}\sin(\varphi) \right], $$ (15b) $$ \boldsymbol{\hat{P}}_{z}=-\boldsymbol{\hat{z}}\frac{i \hbar \rho}{\rho^{2} +R^{2}}\frac{d}{d\varphi}. $$ (15c)In terms of the dimensionless position variable φ , we are required to evaluate \(T^{g\rightarrow f}_{j} =\rho \int _{0}^{2\pi N}\psi _{f}^{\ast } P_{j} \psi _{g} d\varphi \), and upon substituting in from Eq. 4 we find
$$ {\begin{aligned} T^{g\rightarrow f}_{x} &=\frac{i \hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\ &\quad\left.-c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16a) $$ {\begin{aligned} T^{g\rightarrow f}_{y} &=\frac{\hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\&\left.\quad+c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16b) $$ T^{g\rightarrow f}_{z} =\frac{\hbar \rho}{\left(\rho^{2} + R^{2} \right)} \sum_{m} c_{m}^{\ast (f)} c_{m}^{(g)} (q+m). $$ (16c)We see from Eqs. 16a and 16b that light linearly polarized transverse to the helix axis couples coefficients with angular momentum differing by unity Δ m =± 1, whereas from Eq. 16c, linear polarization parallel to the helix axis couples only Δ m =0. In Fig. 5, we plot the absolute square of the momentum operator matrix element between the lowest three bands for linearly polarized light propagating perpendicular to the helix axis (i.e. with z -polarisatie). Initially, for A g =C ⊥ =0, transitions between the ground and first bands are forbidden (as is to be expected for a unit cell with two equivalent wells resulting in a doubling of the first Brillouin zone, so it is in fact the same band). As the strength of the doubled period potential A g is increased with respect to B g , transitions become allowed away from q =0 as can be seen from Fig. 5a (following behaviour from the dotted red curve through to the solid blue curve). The parameters are swept through a resonance as we go from the solid to the dashed blue curve, wherein the situation changes drastically. To understand this behaviour, we must consider the special case of q =0. As we traverse this resonance, the energy of the Bloch function with q =0 constructed from the first excited state of the deeper well in the DQW unit cell (p -like) passes below the Bloch function constructed from the ground state in the shallower well (s -like). Consequently, the parity with respect to φ (which is a good quantum number only for q =0 or |q |=1/2) of the two excited states is exchanged resulting in the rapid switch from forbidden to allowed at q =0, wherein the z -polarized inter-subband matrix element becomes non-zero due to the operator \(\boldsymbol {\hat {P}}_{z}\) (see Eq. 15c) now coupling the even ground state with the odd first excited state. We therefore see the opposite behaviour for transitions between the ground and second band in Fig. 5b about q =0. While initially increasing A g allows transitions at q =0 between the ground state and the second excited state when it is p -like, beyond resonance (when the order of the s -like and p -like excited states are swapped) transitions are suppressed. See for example Ref. [88] for a clear picture of this interchange between the ordering of the even and the odd parity excited states. For transitions between the first and second band (Fig. 5c), we observe a large transition centred about q =0 due to the lifting of the m =± 1 degenerate states of the field-free helix by the superlattice potential. The presence of symmetry-breaking C ⊥ ruins the pristine parities of the states at the centre of the Brillouin zone and all transitions are allowed, as shown in the insets of Fig. 5.
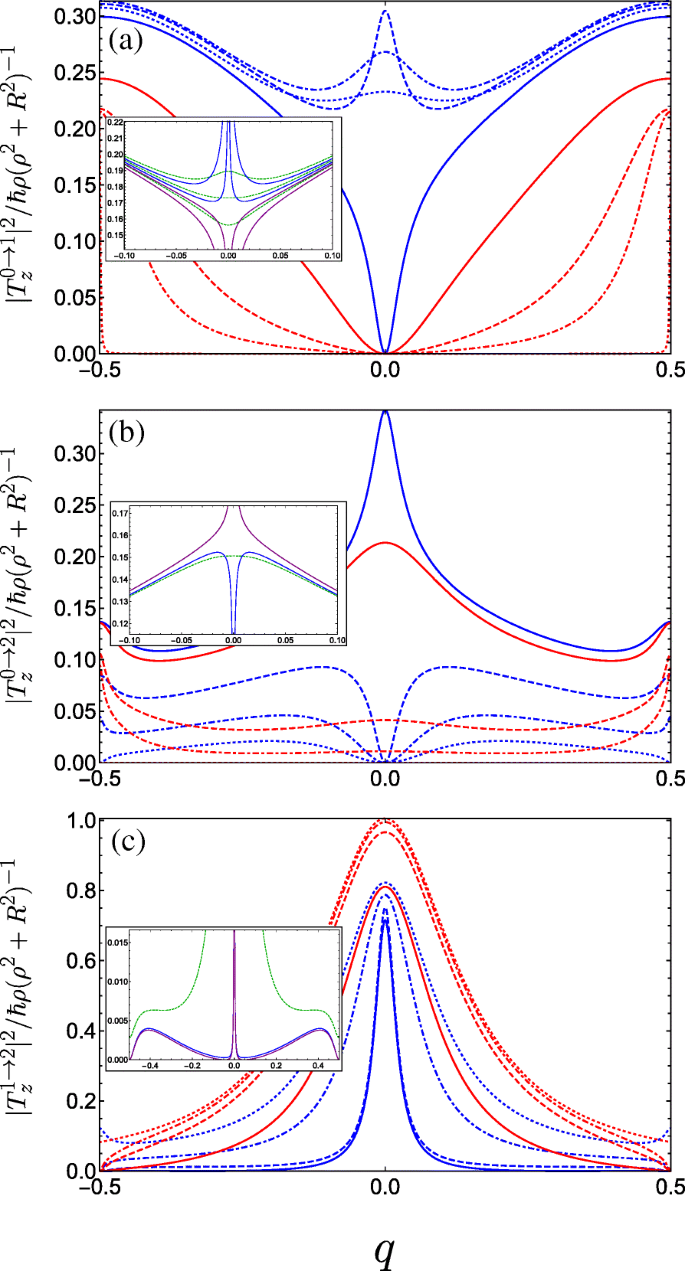
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by linearly z -polarized radiation and for a variety of parameter combinations spanning the first incident of resonance. The different blue curves keep A g =0.5 and C ⊥ =0 fixed and vary B g =0.1, 0.2, and 0.3 corresponding to dot-dashed, dashed, and solid. The different red curves keep B g =0.3 and C ⊥ =0 fixed while varying A g =0.05, 0.1 and 0.3 as dot-dashed, dashed, and solid, while the dotted blue (dotted red) plots the limiting case A g =0.5 &B g →0 (A g →0 &B g =0.3). een Transitions between the ground and first bands. The inset plots the behaviour for fixed A g =0.5 and changing B g crossing the resonant condition at B g =0.25 (see text) in a reduced q -range, ranging from upper blue B g =0.245, lower blue B g =0.249, upper purple B g =0.251, to lower purple B g =0.255. The dashed green curves are for small non-zero transverse field C ⊥ =0.05 ranging from B g =0.245 (upper curve) to B g =0.255 (lower curve) in increments of 0.05. b Plots transitions between the ground and second bands, the inset plots the behaviour close to resonance when A g =0.5; blue is B g =0.249, purple is B g =0.251, and dark green is at resonance with C ⊥ =0.05. c Plots transitions between the first and second bands, the parameters for the inset are the same as those in (b )
In Fig. 6, we plot the absolute square of the momentum operator matrix element for right-handed circularly polarized light which propagates along the helix axis, given by |T x +iT j | 2 . Notably, we observe a large anisotropy between the two halves of the first Brillouin zone, while the result for left-handed polarization is a mirror image to what we see in Fig. 6. Physically, this can be attributed to the conversion of the photon angular momenta to the translational motion of the free charge carriers projected onto the direction of the helix axis, with an unequal population of the excited subband in a preferential momentum direction controlled by the relative handedness of both the helix and the circular polarization of light. An intuitive mechanical analogue would be the rotary motion of Archimedes’ screw being converted into the linear motion of water along the direction of the screw axis dictated by the handedness of the thread. As such, our system of a double-gated nanohelix irradiated by circularly polarized light exhibits a photogalvanic effect, whereby one can choose the net direction of current by irradiating with either right- or left-handed circularly polarized light [44, 45, 89]. This differs from conventional one-dimensional superlattices, wherein the circular photogalvanic effect stems from the spin-orbit term appearing in the effective electron Hamiltonian and is consequently a weaker and hard-to-control phenomenon [90, 91]. The electric current induced by promoting electrons from the ground subband to an excited subband f via the absorption of circularly polarized light can be understood from the equation for the electric current contribution from the f th subband
$$ j_{f} =\frac{e}{2 \pi \rho} \int dq \left[ v_{f}(q) \tau_{f}(q) - v_{g}(q) \tau_{g} (q) \right] \Gamma_{CP}^{g \rightarrow f}(q), $$ (17)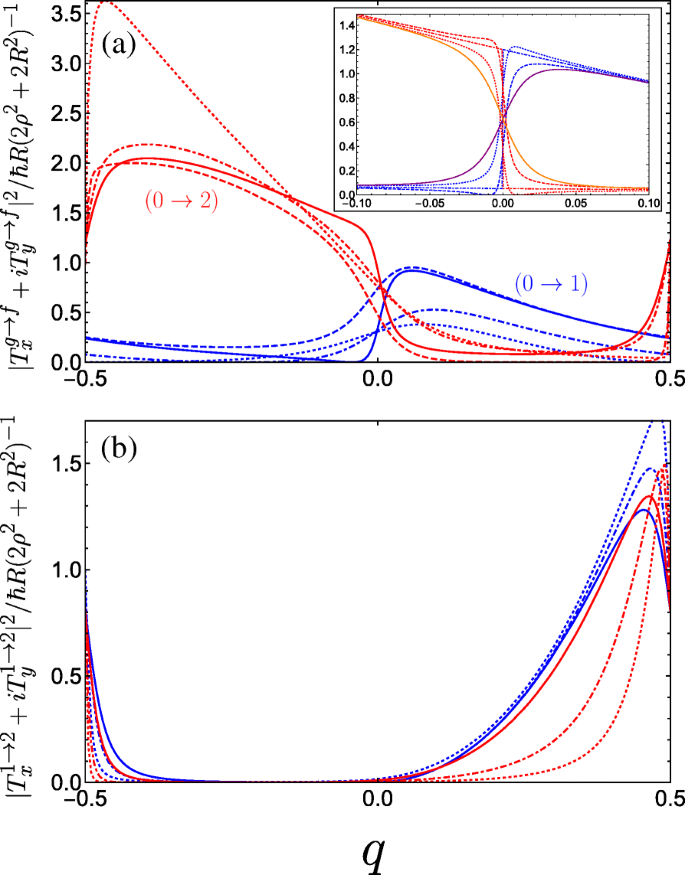
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by right-handed circularly polarized radiation |T x +iT j | 2 and for a variety of parameter combinations spanning the first incident of resonance. een The blue curves denote transitions between the ground and first band while the red curves denote transitions between the ground and second band, both with the following parameters:A g =0.5 and B g =0.3 for solid curves, A g =0.5 and B g =0.1 for dashed curves, A g =0.3 and B g =0.3 for dot-dashed curves, and A g =0.01 and B g =0.3 for dotted curves (as A g →0 the maximum of the 0→2 increases rapidly as it approaches q =− 1/2). The inset plots the behaviour as B g is tuned through resonance for A g =0.5; dotted is B g =0.24, dot-dashed is B g =0.25, and dashed is B g =0.26. The solid purple (orange) curve denotes transitions between the ground and first (second) band at resonance with C ⊥ =0.05 applied. b Plots transitions between the first and second bands. The different blue curves keep A g =0.5 fixed and vary B g =0, 0.2, and 0.3 corresponding to dotted, dot-dashed, and solid. The different red curves keep B g =0.3 fixed while varying A g =0.05, 0.1, and 0.3 as dotted, dot-dashed, and solid. We have omitted plots for C ⊥ ≠0 here as it yields no great qualitative change to the matrix elements
where \(v_{g,f}(q)=(\rho /\hbar)\partial \varepsilon _{g,f}/\partial q \) is the antisymmetric electron velocity v (q )=− v (− q ) (which we can deduce from the symmetric dispersion curves), τ g,f (q ) is a phenomenological relaxation time, and \(\Gamma _{CP}^{g \rightarrow f}(q)\) is the transition rate resulting from the optical perturbation of the electron system. Given that \(\Gamma _{CP}^{g \rightarrow f}(q) \propto |T_{x}^{g \rightarrow f} + i T_{y}^{g \rightarrow f}|^{2}\) for right-handed circularly polarized light where T x en T j are given by Eqs. 16a and 16b, respectively. The anisotropy present in Fig. 6a enters Eq. 17 to yield a non-zero photocurrent. This current flows in the opposite direction for left-handed polarization. Such a circular photogalvanic effect is also exhibited in chiral carbon nanotubes under circularly polarized irradiation [92, 93], although tunability predominantly stems from manipulating the nanotube physical parameters, which are hard to control. The double-gated nanohelix system offers superior versatility by fully controlling the landscape of the superlattice potential, which can be used to tailor the non-equilibrium asymmetric distribution function of photoexcited carriers (as shown in Fig. 6 for inter-subband transitions between the three lowest subbands).
On a side note, we expect that (as with chiral carbon nanotubes [93–95]) the application of a magnetic field along the nanohelix axis can take up the role played by circularly polarized radiation, whereby the current is induced by a magnetic-field-induced asymmetric energy dispersion—which in turn produces an anisotropic electron velocity distribution across the two halves of the Brillouin zone.
Conclusies
In summary, we have shown that the system of a nanohelix between two aligned gates modelled as charged wires is a tunable binary superlattice. The band structure for this system exhibits a diverse behaviour, in particular revealing energy band crossings accessible via tuning the voltages on the gates. The application of an electric field normal to the plane defined by the gates and the helix axis introduces an additional parameter with which to open a band gap at these crossings. Engineering the band structure in situ with the externally induced superlattice potential along a nanohelix provides a clear advantage over conventional heterostructure superlattices with a DQW basis [96, 97]. Both systems can be used as high-responsivity photodetectors, wherein tailoring the band structure (to the so-called band-aligned basis [98–100]) can lead to a reduction in the accompanying dark current. Here control over the global depth of the quantum wells also permits versatility over the detection regime, which can lie within the THz range. We have also investigated the corresponding behaviour of electric dipole transitions between the lowest three subbands induced by both linearly and circularly polarized light, which additionally allows this system to be used for polarization sensitive detection. Finally, the ability to tune the system such that a degenerate excited state is optically accessible from the ground state, along with the inherent chirality present in the light-matter interactions, may make this a promising system for future quantum information processing applications [101]. It is hoped that with the advent of sophisticated nano-fabrication capabilities [102], fully controllable binary superlattice properties will be realized in a nanohelix and will undoubtedly contribute to novel optoelectronic applications.
Appendix
Touching energy bands at Brillouin zone boundary when A g =C ⊥ =0
Here, we show using matrix algebra that in the picture of a binary superlattice pairs of subbands touch at the Brillouin zone edges if A g =C ⊥ =0 and B g ≠0, as seen from the solid blue curves in Fig. 3a. Equation 5 is equivalent to the following N -by-N pentadiagonal matrix Hamiltonian with zeros on the leading sub- and superdiagonals:
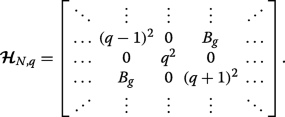 (18)
(18) Let us consider q =1/2 (we could alternatively take q =− 1/2) which makes the leading diagonal symmetric. We can then express this matrix Hamiltonian \(\widetilde {\mathcal {\boldsymbol {H}}}_{N} \equiv \boldsymbol {\mathcal {H}}_{N,q=1/2} \) in block form as
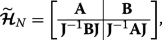 (19)
(19) waar
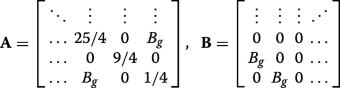 (20)
(20) are both of dimension N /2-by- N /2, and J is the exchange matrix. We may construct a matrix via permuting \(\boldsymbol {\mathcal {H}}_{N}\) with the N -by-N permutation matrix \(\boldsymbol {\mathcal {P}}_{N}\),
$$ \boldsymbol{\mathcal{P}}_{N} =\left[ \begin{array}{cccccc} 1 &0 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &\hdots &1 \\ 0 &1 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &1 &0 \\ \vdots &&&&&\vdots \\ 0 &\hdots &\hdots &1 &\hdots &0 \\ \end{array} \right], $$ (21)such that the permutation-similar matrix is
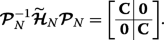 (22)
(22) Hence, the eigenvalues of \(\boldsymbol {\mathcal {P}}_{N}^{-1}\widetilde {\boldsymbol {\mathcal {H}}}_{N} \boldsymbol {\mathcal {P}}_{N}\), which are the same as the eigenvalues \(\widetilde {\boldsymbol {\mathcal {H}}}_{N}\), are double degenerate with the values given by the eigenvalue spectrum of the tridiagonal matrix C
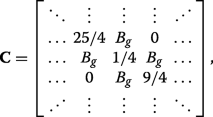 (23)
(23) which can also be expressed succinctly in terms of the previously defined matrices via \(\mathbf {C}=\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {A}\boldsymbol {\mathcal {P}}_{N/2}+\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {B}\mathbf {J}\boldsymbol {\mathcal {P}}_{N/2}^{4}\). We can see that applying C ⊥ ≠0 (inset of Fig. 3a) or both C ⊥ en A g ≠0 (inset of Fig. 3b) ruins the symmetry in the matrix Hamiltonian and prevents the existence of eigenvalues with multiplicity beyond unity, resulting in the appearance of band gaps.
Energy crossing at centre of Brillouin zone between third and forth subbands
As an example, let us specifically consider the case where p =2, wherein the matrices (12) and (13) become:
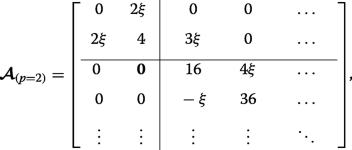 (24)
(24) and
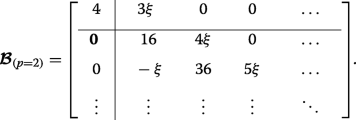 (25)
(25) This case corresponds to the crossings of the blue curves at the edge of the Brillouin zone in Fig. 3d (whereas p =0 results in crossings at q =0 in Fig. 3b). The lower eigenvalues are found exactly by diagonalizing each of the two finite matrices and they interlace, yielding \(\eta _{0,1,2} =2-\sqrt {4+4\xi ^{2}}, 4, 2+\sqrt {4+4\xi ^{2}}\). The infinite lower-right-hand block tridiagonal matrices coincide, thus the remaining double degenerate eigenvalues are found by approximately or numerically solving Det[D −η I ]=0.
Beschikbaarheid van gegevens en materialen
The data for the figures all stem from numerically diagonalizing the matrix described by Eq. 5 and can readily be achieved in any numerical software package. With this in mind, the datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Nanomaterialen
- 3-bits binaire teller
- Decimaal versus binaire nummering
- Octale en hexadecimale nummering
- Binaire toevoeging
- Negatieve binaire getallen
- Binair aftrekken
- Binaire overloop
- Binaire telreeks
- Een binaire opteller
- Boorkoolstofoxynitride als een nieuwe metaalvrije fotokatalysator
- Aan de slag met Go op PLCnext



