Mesh huidige methode en analyse

De Mesh-Current-methode , ook bekend als de Loop Current Method , lijkt veel op de Branch Current-methode omdat het gelijktijdige vergelijkingen, de spanningswet van Kirchhoff en de wet van Ohm gebruikt om onbekende stromen in een netwerk te bepalen. Het verschilt van de Branch Current-methode doordat het niet . doet gebruik de huidige wet van Kirchhoff en het is meestal in staat om een ​​circuit op te lossen met minder onbekende variabelen en minder gelijktijdige vergelijkingen, wat vooral fijn is als je gedwongen bent om op te lossen zonder rekenmachine.

Mesh Current, conventionele methode

Laten we eens kijken hoe deze methode werkt op hetzelfde voorbeeldprobleem:

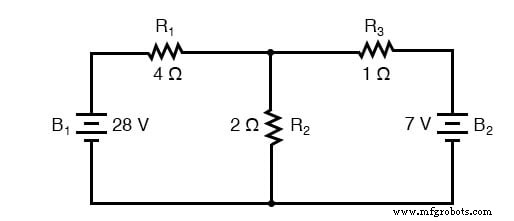
Lussen identificeren

De eerste stap in de Mesh Current-methode is het identificeren van "lussen" binnen het circuit dat alle componenten omvat. In ons voorbeeldcircuit wordt de lus gevormd door B₁ , R₁ , en R₂ zal de eerste zijn terwijl de lus gevormd door B₂ , R₂ , en R₃ zal de tweede zijn. Het vreemdste deel van de Mesh Current-methode is het visualiseren van circulerende stromen in elk van de lussen. In feite dankt deze methode zijn naam aan het idee dat deze stromen in elkaar grijpen tussen lussen, zoals sets draaiende tandwielen:

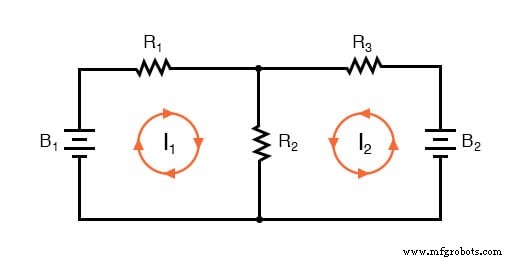
De keuze van de richting van elke stroom is geheel willekeurig, net als bij de Branch Current-methode, maar de resulterende vergelijkingen zijn gemakkelijker op te lossen als de stromen in dezelfde richting gaan door kruisende componenten (merk op hoe stromen I₁ en ik₂ gaan beide "omhoog" door weerstand R₂ , waar ze "in elkaar grijpen" of elkaar kruisen). Als de veronderstelde richting van een maasstroom verkeerd is, zal het antwoord voor die stroom een ​​negatieve waarde hebben.

Label de polariteiten van de spanningsdaling

De volgende stap is om alle spanningsvalpolariteiten over weerstanden te labelen volgens de veronderstelde richtingen van de maasstromen. Onthoud dat het "stroomopwaartse" uiteinde van een weerstand altijd negatief zal zijn en het "stroomafwaartse" uiteinde van een weerstand positief ten opzichte van elkaar, aangezien elektronen negatief geladen zijn. De batterijpolariteiten worden natuurlijk bepaald door hun symbooloriëntaties in het diagram en kunnen al dan niet "eens" zijn met de weerstandspolariteiten (veronderstelde stroomrichtingen):

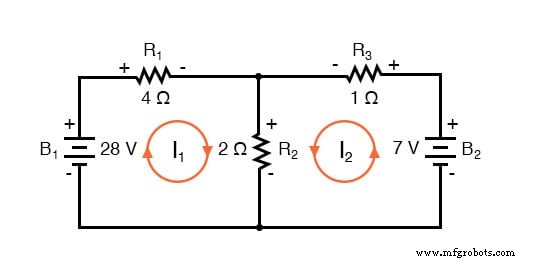
Met behulp van de spanningswet van Kirchhoff kunnen we nu om elk van deze lussen stappen en vergelijkingen genereren die representatief zijn voor de spanningsdalingen en polariteiten van de componenten. Net als bij de Branch Current-methode, zullen we de spanningsval van een weerstand aanduiden als het product van de weerstand (in ohm) en de respectieve maasstroom (die hoeveelheid is op dit moment onbekend). Waar twee stromen in elkaar grijpen, zullen we die term in de vergelijking schrijven met weerstandsstroom als de som van de twee in elkaar grijpende stromen.

De linkerlus van het circuit volgen met vergelijkingen

De linkerlus van het circuit volgen, beginnend vanuit de linkerbovenhoek en tegen de klok in bewegend (de keuze van startpunten en richtingen is uiteindelijk niet relevant), polariteit tellen alsof we een voltmeter in de hand hebben, rode draad op het punt voor ons en zwarte draad op het punt erachter, krijgen we deze vergelijking:

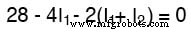
Merk op dat de middelste term van de vergelijking de som van maasstromen I₁ . gebruikt en ik₂ als de stroom door weerstand R₂ . Dit komt omdat maasstromen I₁ en ik₂ gaan dezelfde richting uit via R₂ en vullen elkaar zo aan. De coëfficiënt van 2 verdelen over de I₁ en ik₂ termen, en dan I₁ . combineren termen in de vergelijking, kunnen we als zodanig vereenvoudigen:

Op dit moment hebben we één vergelijking met twee onbekenden. Om twee onbekende maasstromen op te lossen, moeten we twee vergelijkingen hebben. Als we de andere lus van het circuit volgen, kunnen we een andere KVL-vergelijking verkrijgen en voldoende gegevens hebben om de twee stromen op te lossen. Gewoontedier dat ik ben, ik begin in de linkerbovenhoek van de rechterlus en volg tegen de klok in:

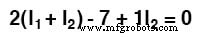
Door de vergelijking te vereenvoudigen zoals eerder, eindigen we met:

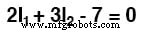
Oplossen voor het onbekende

Met twee vergelijkingen kunnen we nu een van de verschillende methoden gebruiken om de onbekende stromen I₁ wiskundig op te lossen. en ik₂ :

Circuit opnieuw tekenen

Wetende dat deze oplossingen waarden zijn voor mesh stromingen, niet tak stromen, moeten we teruggaan naar ons diagram om te zien hoe ze bij elkaar passen om stromen door alle componenten te geven:

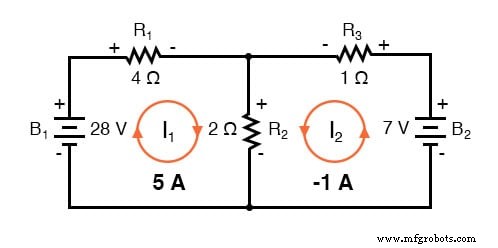
De oplossing van -1 amp voor I₂ betekent dat we aanvankelijk dachten dat de stroomrichting niet klopte. In werkelijkheid, ik₂ stroomt tegen de klok in met een waarde van (positief) 1 ampère:

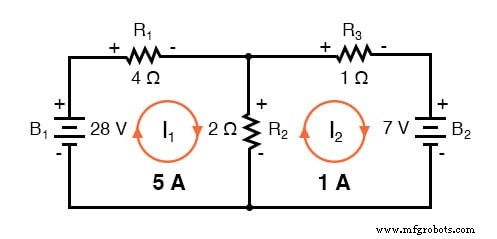
Deze verandering van stroomrichting ten opzichte van wat eerst werd aangenomen, zal de polariteit van de spanningsdalingen over R₂ veranderen en R₃ vanwege huidige I₂ . Vanaf hier kunnen we zeggen dat de stroom door R₁ is 5 ampère, met de spanningsval over R₁ zijnde het product van stroom en weerstand (E=IR), 20 volt (positief aan de linkerkant en negatief aan de rechterkant).

We kunnen ook gerust stellen dat de stroom door R₃ is 1 ampère, met een spanningsval van 1 volt (E=IR), positief links en negatief rechts. Maar wat gebeurt er op R₂ ?

Maasstroom I₁ gaat "naar beneden" via R₂ , terwijl mesh stroom I₂ gaat "omhoog" via R₂ . Om de werkelijke stroom te bepalen via R₂ , we moeten zien hoe maasstromen I₁ en ik₂ interageren (in dit geval zijn ze in oppositie) en voegen ze algebraïsch toe om tot een uiteindelijke waarde te komen. Sinds ik₁ gaat "down" bij 5 ampère, en I₂ gaat omhoog bij 1 ampère, de echte stroom door R₂ moet een waarde van 4 ampère zijn, naar beneden gaand:

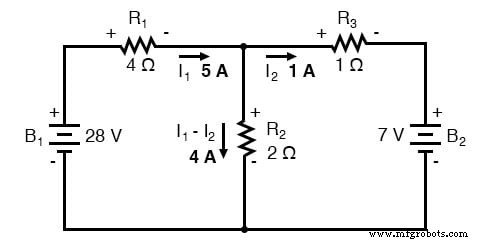
Een stroom van 4 ampère door R₂ 's weerstand van 2 Ω geeft ons een spanningsval van 8 volt (E=IR), positief aan de bovenkant en negatief aan de onderkant.

Voordeel van mesh-stroomanalyse

Het belangrijkste voordeel van Mesh Current-analyse is dat het over het algemeen de oplossing van een groot netwerk mogelijk maakt met minder onbekende waarden en minder gelijktijdige vergelijkingen. Ons voorbeeldprobleem had drie vergelijkingen nodig om de Branch Current-methode op te lossen en slechts twee vergelijkingen met behulp van de Mesh Current-methode. Dit voordeel is veel groter naarmate netwerken complexer worden:

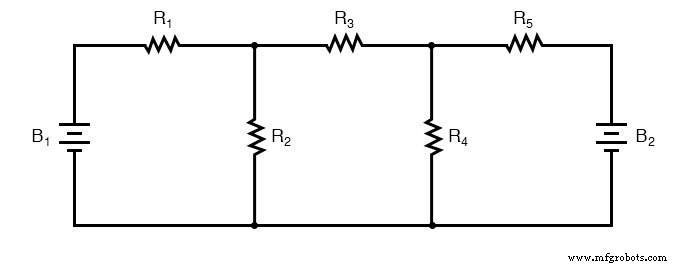
Om dit netwerk op te lossen met behulp van vertakkingsstromen, moeten we vijf variabelen vaststellen om rekening te houden met elke unieke stroom in het circuit (I₁ via I₅ ). Hiervoor zijn vijf vergelijkingen nodig voor de oplossing, in de vorm van twee KCL-vergelijkingen en drie KVL-vergelijkingen (twee vergelijkingen voor KCL op de knooppunten en drie vergelijkingen voor KVL in elke lus):

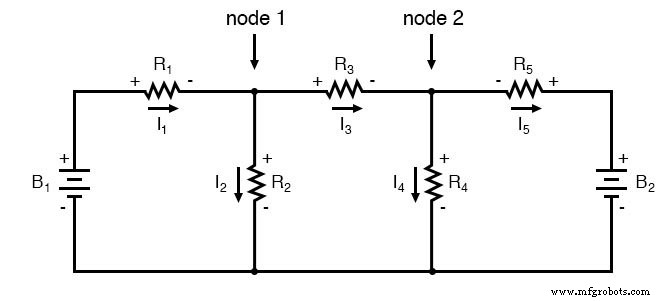
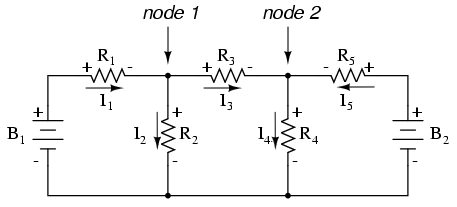
Ik veronderstel dat als je niets beters te doen hebt met je tijd dan het oplossen van vijf onbekende variabelen met vijf vergelijkingen, je het misschien niet erg vindt om de Branch Current-analysemethode voor dit circuit te gebruiken. Voor degenen onder ons die hebben betere dingen om te doen met onze tijd, de Mesh Current-methode is een stuk eenvoudiger en vereist slechts drie onbekenden en drie vergelijkingen om op te lossen:

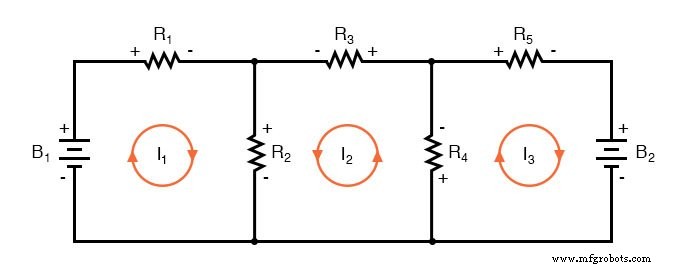
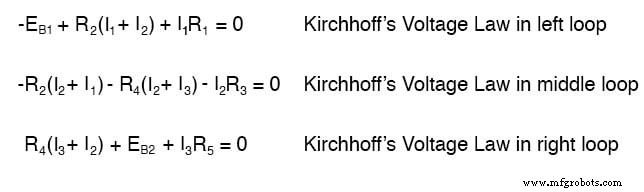
Minder vergelijkingen om mee te werken is een duidelijk voordeel, vooral bij het uitvoeren van een gelijktijdige vergelijkingsoplossing met de hand (zonder rekenmachine).

Ongebalanceerde Wheatstone-brug

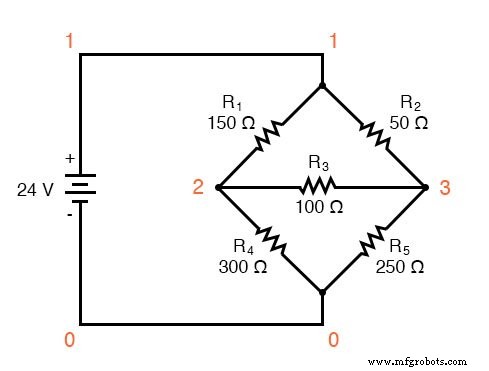
Een ander type circuit dat zich goed leent voor Mesh Current is de ongebalanceerde Wheatstone Bridge. Neem bijvoorbeeld dit circuit:

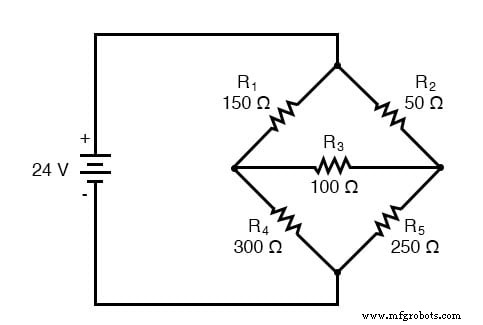
Aangezien de verhoudingen van R₁ /R₄ en R₂ /R₅ ongelijk zijn, weten we dat er spanning zal staan ​​over weerstand R₃ , en een hoeveelheid stroom erdoorheen. Zoals aan het begin van dit hoofdstuk is besproken, is dit type circuit onherleidbaar door normale serie-parallelle analyse en kan het alleen met een andere methode worden geanalyseerd.

We zouden de Branch Current-methode op dit circuit kunnen toepassen, maar daarvoor zijn zes . nodig stromingen (I₁ via I₆ ), wat leidt tot een zeer groot aantal gelijktijdige vergelijkingen om op te lossen. Met behulp van de Mesh Current-methode kunnen we echter alle stromen en spanningen oplossen met veel minder variabelen.

Netwerk tekenen

De eerste stap in de Mesh Current-methode is om net genoeg mesh-stromen te trekken om rekening te houden met alle componenten in het circuit. Als we naar ons brugcircuit kijken, zou het duidelijk moeten zijn waar we twee van deze stromen moeten plaatsen:

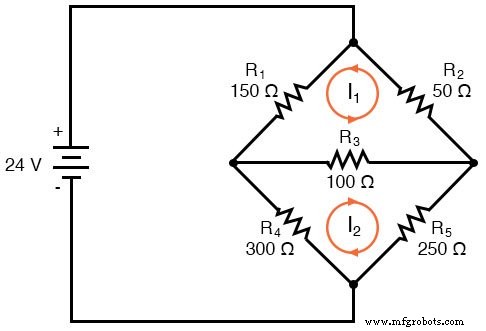
De richtingen van deze maasstromen zijn natuurlijk willekeurig. Twee maasstromen zijn echter niet genoeg in dit circuit, omdat geen van beide I₁ noch ik₂ gaat door de batterij. We moeten dus een derde maasstroom toevoegen, I₃ :

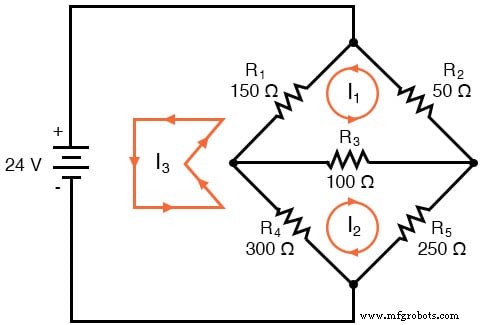
Hier heb ik I₃ . gekozen om te lussen vanaf de onderkant van de batterij, via R₄ , via R₁ en terug naar de bovenzijde van de batterij. Dit is niet het enige pad dat ik had kunnen kiezen voor I₃ , maar het lijkt het eenvoudigst.

Label de polariteiten van de spanningsdaling van de weerstand

Nu moeten we de polariteiten van de spanningsval van de weerstand labelen, waarbij we elk van de veronderstelde stroomrichtingen volgen:

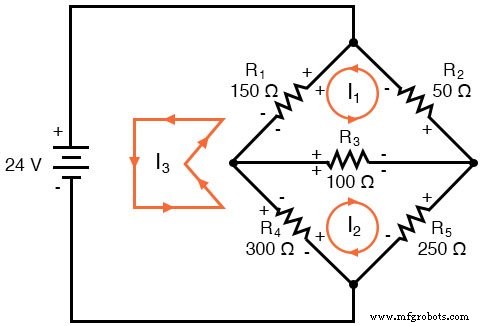
Let hier op iets heel belangrijks:bij weerstand R₄ , komen de polariteiten voor de respectievelijke maasstromen niet overeen. Dit komt omdat die maasstromen (I₂ en ik₃ ) doorlopen R₄ in verschillende richtingen. Dit sluit het gebruik van de Mesh Current-analysemethode niet uit, maar maakt het wel een beetje ingewikkeld. Maar we zullen later laten zien hoe je de R₄ . kunt vermijden huidige botsing. (Zie voorbeeld hieronder)

KVL gebruiken

Een KVL-vergelijking genereren voor de bovenste lus van de brug, beginnend bij het bovenste knooppunt en met de klok mee volgen:

In deze vergelijking vertegenwoordigen we de gemeenschappelijke richtingen van stromen door hun sommen via gemeenschappelijke weerstanden. Bijvoorbeeld weerstand R₃ , met een waarde van 100 Ω, wordt de spanningsval weergegeven in de bovenstaande KVL-vergelijking door de uitdrukking 100(I₁ + I₂ ), aangezien beide stromen I₁ en ik₂ ga door R₃ van rechts naar links. Hetzelfde kan gezegd worden voor weerstand R₁ , met de spanningsval-expressie weergegeven als 150(I₁ + I₃ ), aangezien zowel I₁ en ik₃ ga van onder naar boven door die weerstand, en werk zo samen om de spanningsval te genereren.

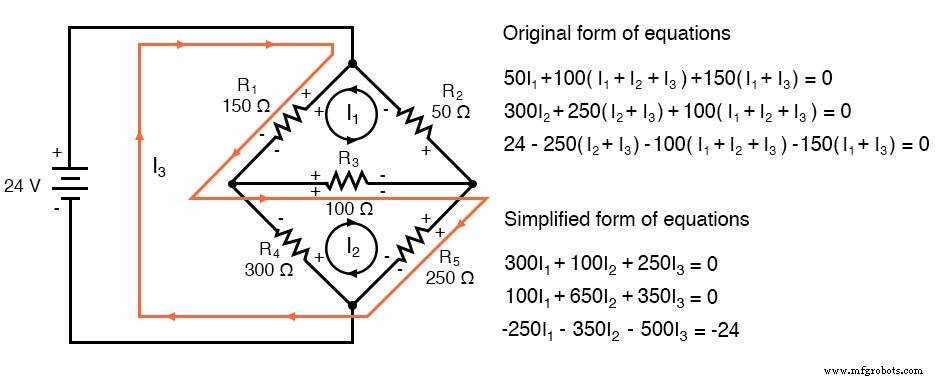
Het genereren van een KVL-vergelijking voor de onderste lus van de brug zal niet zo eenvoudig zijn, omdat we twee stromen tegen elkaar hebben door weerstand R₄ . Hier is hoe ik het doe (beginnend bij het rechter knooppunt en tegen de klok in volgen):

Merk op hoe de tweede term in de oorspronkelijke vorm van de vergelijking weerstand R₄ . heeft ‘s waarde van 300 Ω vermenigvuldigd met het verschil tussen I₂ en ik₃ (I₂ - Ik₃ ). Dit is hoe we het gecombineerde effect weergeven van twee maasstromen die in tegengestelde richtingen door dezelfde component gaan. Het kiezen van de juiste wiskundige tekens is hier erg belangrijk:300(I₂ - Ik₃ ) betekent niet hetzelfde als 300(I₃ - Ik₂ ). Ik heb ervoor gekozen om 300(I₂ . te schrijven - Ik₃ ) omdat ik eerst aan I₂ . dacht 's effect (creëren van een positieve spanningsval, meten met een denkbeeldige voltmeter over R₄ , rode draad aan de onderkant en zwarte draad aan de bovenkant), en in tweede instantie van I₃ 's effect (creëren van een negatieve spanningsval, rode draad aan de onderkant en zwarte draad aan de bovenkant). Als ik had gedacht in termen van I₃ 's effect eerst en I₂ 's effect secundair, mijn denkbeeldige voltmeter-leads in dezelfde posities houden (rood aan de onderkant en zwart aan de bovenkant), de uitdrukking zou zijn geweest -300(I₃ - Ik₂ ). Merk op dat deze uitdrukking is wiskundig equivalent aan de eerste:+300(I₂ - Ik₃ ).

Nou, dat zorgt voor twee vergelijkingen, maar ik heb nog steeds een derde vergelijking nodig om mijn gelijktijdige vergelijkingsset van drie variabelen, drie vergelijkingen, te voltooien. Deze derde vergelijking moet ook de spanning van de batterij bevatten, die tot nu toe in geen van de twee voorgaande KVL-vergelijkingen voorkomt. Om deze vergelijking te genereren, zal ik opnieuw een lus volgen met mijn denkbeeldige voltmeter, beginnend bij de onderste (negatieve) pool van de batterij, met de klok mee stappen (nogmaals, de richting waarin ik stap is willekeurig en hoeft niet hetzelfde te zijn als de richting van de maasstroom in die lus):

Oplossen voor de stromingen

Oplossen voor I₁ , ik₂ , en ik₃ met behulp van welke gelijktijdige vergelijkingsmethode we ook verkiezen:

Voorbeeld: Gebruik Octave om de oplossing voor I₁ . te vinden , ik₂ , en ik₃ van de hierboven vereenvoudigde vorm van vergelijkingen.

Oplossing: In Octave, een open-source Matlab®-kloon, voert u de coëfficiënten in de A-matrix in tussen vierkante haken met kolomelementen door komma's gescheiden en rijen door puntkomma's gescheiden. Voer de spanningen in de kolomvector in:b. De onbekende stromingen:I₁ , ₂ , en ik₃ worden berekend met het commando:x=A\b. Deze bevinden zich in de x-kolomvector.

 octaaf:1>A =[300,100,150;100,650,-300;-150,300,-450] A =300 100 150 100 650 -300 -150 300 -450 octaaf:2> b =[0;0;-24] b =0 0 -24 octaaf:3> x =A\b x =-0.093793 0,077241 0,136092 

De negatieve waarde die is bereikt voor I₁ vertelt ons dat de veronderstelde richting voor die maasstroom onjuist was. De werkelijke stroomwaarden door elke weerstand zijn dus als volgt:

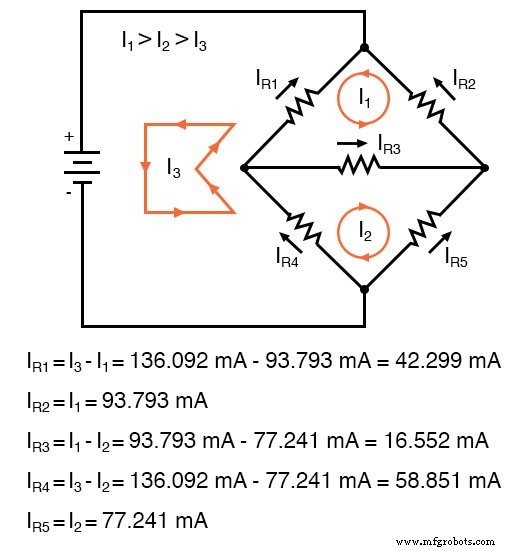
Berekenen van spanningsdalingen over elke weerstand:

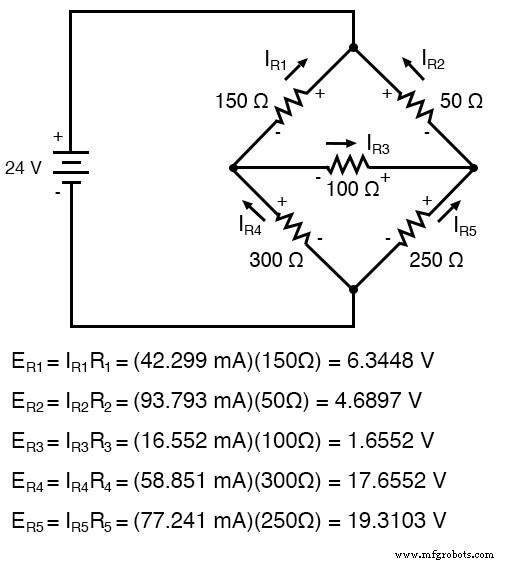
Een SPICE-simulatie bevestigt de nauwkeurigheid van onze spanningsberekeningen:

ongebalanceerde brug van tarwesteen v1 1 0 r1 1 2 150 r2 1 3 50 r3 2 3 100 r4 2 0 300 r5 3 0 250 .dc v1 24 24 1 .print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0) .einde v1 v(1,2) v(1,3) v(3,2) v(2) v(3) 2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01 

Voorbeeld:

(a) Vind een nieuw pad voor huidige I₃ die op geen enkele weerstand een tegenstrijdige polariteit produceert in vergelijking met I₁ of ik₂ . R₄ was de beledigende component. (b) Vind waarden voor I₁ , ik₂ , en ik₃ . (c) Zoek de vijf weerstandsstromen en vergelijk ze met de vorige waarden.

Oplossing:

(a) Route I₃ via R₅ , R_3, en R₁ zoals getoond:

Merk op dat de tegenstrijdige polariteit op R₄ is verwijderd. Bovendien heeft geen van de andere weerstanden tegenstrijdige polariteiten.

(b) Octave, een open source (gratis) Matlab-kloon, levert een mesh-stroomvector op "x":

 octaaf:1> A =[300,100,250;100,650,350;-250,-350,-500] A =300 100 250 100 650 350 -250 -350 -500 octaaf:2> b =[0;0;-24] b =0 0 -24 octaaf:3> x =A\b x =-0.093793 -0.058851 0,136092 

Niet alle stromen I₁ , ik₂ , en ik₃ zijn hetzelfde (I₂ ) als de vorige brug vanwege verschillende luspaden De weerstandsstromen zijn echter vergelijkbaar met de vorige waarden:

 IR1 =I1 + I3 =-93.793 ma + 136.092 ma =42.299 ma IR2 =I1 =-93.793 ma IR3 =I1 + I2 + I3 =-93.793 ma -58.851 ma + 136.092 ma =-16.552 ma IR4 =I2 =-58.851 ma IR5 =I2 + I3 =-58.851 ma + 136.092 ma =77.241 ma 

Aangezien de weerstandsstromen hetzelfde zijn als de vorige waarden, zullen de weerstandsspanningen identiek zijn en hoeven ze niet opnieuw te worden berekend.

BEOORDELING:

• Te volgen stappen voor de analysemethode "Mesh Current":
• (1) Teken maasstromen in lussen van het circuit, genoeg om rekening te houden met alle componenten.
• (2) Label weerstandsspanningsvalpolariteiten op basis van veronderstelde richtingen van maasstromen.
• (3) Schrijf KVL-vergelijkingen voor elke lus van het circuit, waarbij je het product IR vervangt door E in elke weerstandsterm van de vergelijking. Waar twee maasstromen door een component snijden, druk de stroom dan uit als de algebraïsche som van die twee maasstromen (d.w.z. I₁ + I₂ ) als de stromen door die component in dezelfde richting gaan. Zo niet, druk dan de stroom uit vanaf het verschil (d.w.z. I₁ - Ik₂ ).
• (4) Oplossen voor onbekende maasstromen (gelijktijdige vergelijkingen).
• (5) Als een oplossing negatief is, dan is de veronderstelde stroomrichting verkeerd!
• (6) Voeg algebraïsch maasstromen toe om huidige componenten te vinden die meerdere maasstromen delen.
• (7) Oplossen voor spanningsdalingen over alle weerstanden (E=IR).

Netstroom door inspectie

We kijken nog een keer naar de "mesh current-methode" waarbij alle stromen met de klok mee (cw) lopen. De motivatie is om het schrijven van maasvergelijkingen te vereenvoudigen door de polariteit van de spanningsval van de weerstand te negeren. We moeten echter letten op de polariteit van spanningsbronnen met betrekking tot de veronderstelde stroomrichting. Het teken van de weerstandsspanningsdalingen zal een vast patroon volgen.

Als we een reeks conventionele maasstroomvergelijkingen schrijven voor het onderstaande circuit, waarbij we wel letten op de tekenen van de spanningsval over de weerstanden, kunnen we de coëfficiënten herschikken in een vast patroon:

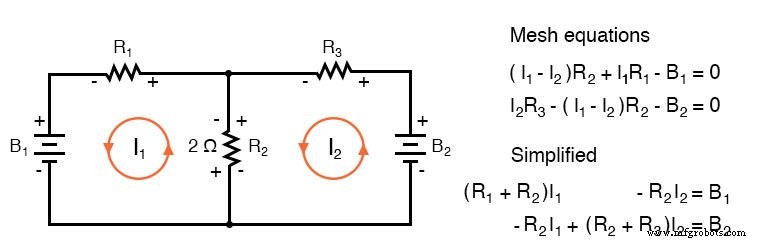
Eenmaal herschikt, kunnen we vergelijkingen schrijven door inspectie. De tekens van de coëfficiënten volgen een vast patroon in het bovenstaande paar of de set van drie in de onderstaande regels.

Huidige regels mesh:

• Deze methode gaat uit van conventionele stroomstroomspanningsbronnen. Vervang elke stroombron parallel door een weerstand met een equivalente spanningsbron in serie met een equivalente weerstand.
• Negeer de stroomrichting of spanningspolariteit op weerstanden en teken tegen de klok in stroomlussen die door alle componenten lopen. Vermijd geneste lussen.
• Schrijf spanningswetvergelijkingen in termen van onbekende stromen:I₁ , ik₂ , en ik₃ . Vergelijking 1 coëfficiënt 1, vergelijking 2, coëfficiënt 2 en vergelijking 3 coëfficiënt 3 zijn de positieve sommen van weerstanden rond de respectieve lussen.
• Alle andere coëfficiënten zijn negatief, representatief voor de weerstand die een paar lussen gemeen hebben. Vergelijking 1 coëfficiënt 2 is de weerstand die gemeenschappelijk is voor lussen 1 en 2, coëfficiënt 3 de weerstand die gemeenschappelijk is voor lussen 1 en 3. Herhaal dit voor andere vergelijkingen en coëfficiënten.
• +(som van R-lus 1)I1 - (gewone R-lus 1-2)I2 - (algemene R-lus 1-3)I3 =E1
  -(algemene R-lus 1-2)I1 + ( som van R-lus 2)I2 - (gewone R-lus 2-3)I3 =E2
  -(algemene R-lus 1-3)I1 - (algemene R-lus 2-3)I2 + (som van R-lus 3 )I3 =E3
• De rechterkant van de vergelijkingen is gelijk aan een elektronenstroom-vloeispanningsbron. Een spanningsstijging ten opzichte van de veronderstelde stroom tegen de klok in is positief en 0 voor geen spanningsbron.
• Vergelijkingen voor maasstromen oplossen:I₁ , ik₂ , en I3. Oplossen voor stromen door individuele weerstanden met KCL. Los spanningen op met de wet van Ohm en KVL.

Hoewel de bovenstaande regels specifiek zijn voor een circuit met drie mazen, kunnen de regels worden uitgebreid tot kleinere of grotere mazen. Onderstaande figuur illustreert de toepassing van de regels. De drie stromen worden allemaal in dezelfde richting getrokken, met de klok mee. Voor elk van de drie lussen wordt één KVL-vergelijking geschreven. Merk op dat er geen polariteit op de weerstanden is getekend. We hebben het niet nodig om de tekens van de coëfficiënten te bepalen. Wel moeten we letten op de polariteit van de spanningsbron ten opzichte van de stroomrichting. De I₃ met de klok mee stroomt de stroom uit de (+) positieve pool van de l24V-bron en keert terug naar de (-) terminal. Dit is een spanningsstijging voor conventionele stroom. Daarom is de derde vergelijking aan de rechterkant -24V.

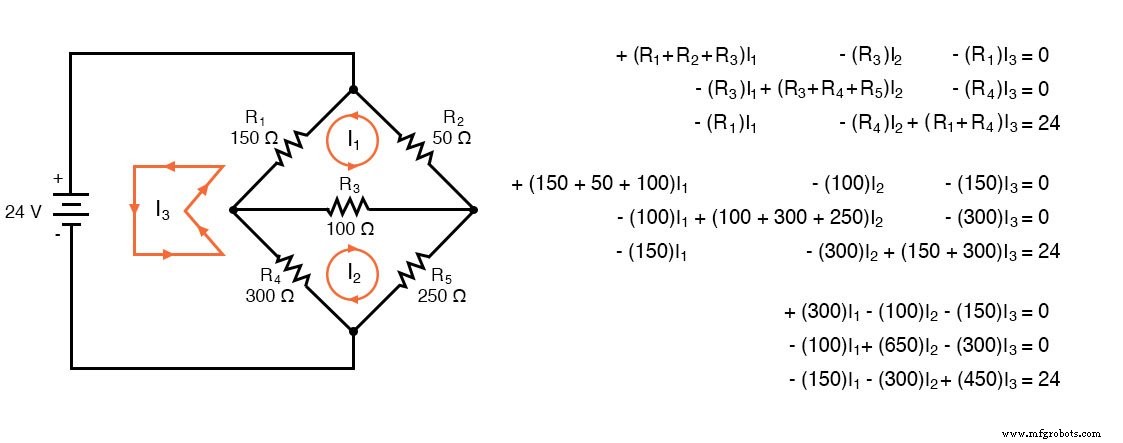
Voer in Octave de coëfficiënten in de A-matrix in met kolomelementen gescheiden door komma's en rijen gescheiden door puntkomma's. Voer de spanningen in de kolomvector b in. Los de onbekende stromen op:I₁ , ik₂ , en ik₃ met het commando:x=A\b. Deze stromen bevinden zich in de x-kolomvector. De positieve waarden geven aan dat de drie maasstromen allemaal in de veronderstelde richting met de klok mee stromen.

 octaaf:2> A=[300,-100,-150;-100,650,-300;-150,-300,450] A =300 -100 -150 -100 650 -300 -150 -300 450 octaaf:3> b=[0;0;24] b =0 0 24 octaaf:4> x=A\b x =0,093793 0,077241 0,136092 

De maasstromen komen overeen met de vorige oplossing door een andere maasstroommethode. De berekening van weerstandsspanningen en -stromen zal identiek zijn aan de vorige oplossing. Het is niet nodig om hier te herhalen.

Houd er rekening mee dat elektrotechnische teksten zijn gebaseerd op conventionele stroom. De loop-current, mesh-current methode in die teksten zal de veronderstelde mesh-stromen uitvoeren met de klok mee . De conventionele stroom vloeit uit de (+) pool van de batterij door het circuit en keert terug naar de (-) pool. Een conventionele stroom-spanningsstijging komt overeen met het traceren van de veronderstelde stroom van (-) naar (+) via spanningsbronnen.

Er volgt nog een voorbeeld van een eerder circuit. De weerstand rond lus 1 is 6 , rond lus 2:3 Ω. De gemeenschappelijke weerstand van beide lussen is 2 . Let op de coëfficiënten van I₁ en ik₂ in het paar vergelijkingen. De veronderstelde stroom van lus 1 met de klok mee volgen via B₁ van (+) tot (-) komt overeen met een stijging van de stroomspanning van de elektronenstroom.

Het teken van de 28 V is dus positief. De lus 2 tegen de klok in veronderstelde stroomsporen (-) tot (+) door B₂ , een spanningsval. Dus het teken van B₂ is negatief, -7 in de 2e mesh-vergelijking. Nogmaals, er zijn geen polariteitsmarkeringen op de weerstanden. Ze komen ook niet voor in de vergelijkingen.

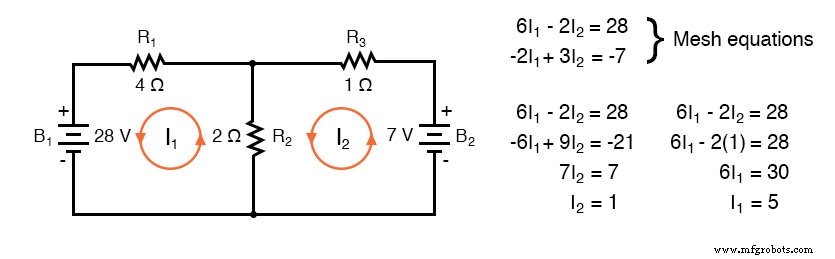
De stromen I₁ =5 A, en ik₂ =1 A zijn beide positief. Ze stromen allebei in de richting van de lussen met de klok mee. Dit is vergelijkbaar met eerdere resultaten.

Samenvatting:

• De aangepaste maasstroommethode vermijdt het bepalen van de tekens van de vergelijkingscoëfficiënten door alle maasstromen met de klok mee te trekken voor conventionele stroomstroming.
• We moeten echter wel het teken van spanningsbronnen in de lus bepalen. De spanningsbron is positief als de veronderstelde ccw-stroom met de batterij (bron) vloeit. Het teken is negatief als de veronderstelde ccw-stroom tegen de batterij vloeit.
• Zie de regels hierboven voor details.

GERELATEERD WERKBLAD:

• Werkblad DC mesh-stroomanalyse